Un programme de conjugaison ou de cryptage comme ceux prévus en cycle 4, manipulent des chaînes de caractères, ou « mots ». Or Emil Post et Andreï Andreïevich Markov ont montré en 1947, que tout calcul peut se mener par des transformations sur des mots.
par Alain Busser, Patrice Debrabant
Motivation
Le document d’Eduscol rappelle fort justement, à propos de programmation, que « l’enseignement de l’informatique au cycle 4 n’a pas pour objectif de former des élèves experts, ni de leur fournir une connaissance exhaustive d’un langage ou d’un logiciel particulier » [1]. Un bon moyen pour éviter cet écueil est de veiller, non seulement à ne pas fournir une connaissance exhaustive mais même une connaissance exclusive d’un langage : Travailler sur plusieurs langages, chacun n’ayant que le minimum d’instructions, c’est-à-dire uniquement celles qui servent au problème étudié [2]. Voici donc un exemple de langage créé spécialement pour cet article :
TOTO est un robot inspiré par les tortues de Bristol ; son langage de programmation ne comprend que ces 4 instructions, notée chacune sur une seule lettre :
- « A » pour « avancer » (de 20 pixels en l’occurence) ;
- « R » pour « reculer » (de 20 pixels toujours) ;
- « D » pour « tourner à droite » (de 90° en l’occurence) ;
- « G » pour « tourner à gauche » (toujours de 90°) ;
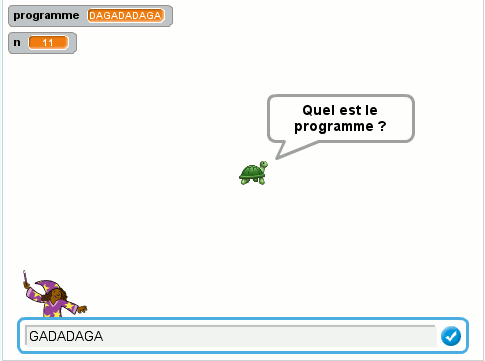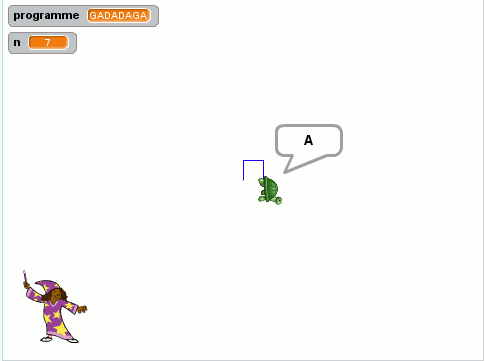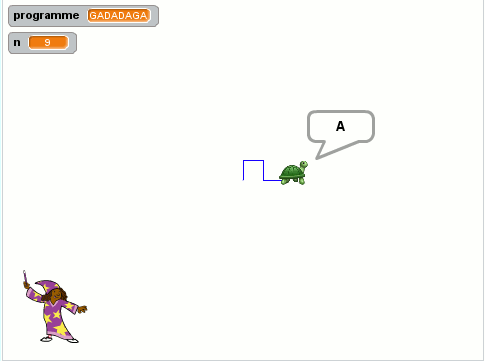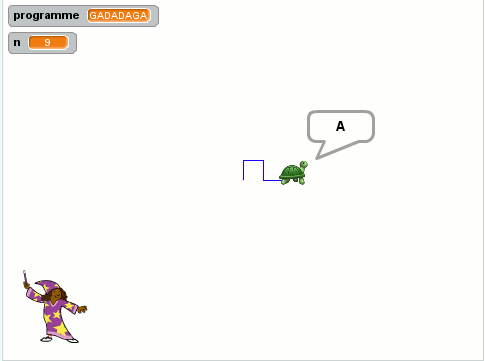
Quel est l’intérêt d’un tel langage (dont on a assez vite fait le tour en tant que tel) ?
L’intérêt réside dans le déplacement des problématiques :
- un programme devient un mot (Oups !... on a basculé dans le littéraire) ;
- la difficulté consiste non pas à écrire un programme mais :
- à écrire un programme qui écrit un programme (!) ; [3]
- à écrire un petit compilateur.
Ce point de vue apporte un éclairage nouveau par rapport à la Programmation Visuelle par blocs.
Dans le cadre du cycle 4 du collège, un programme de conjugaison ou de cryptage manipule des chaînes de caractères, ou « mots ». Ces « jeux de mots » ont un potentiel important : Emil Post et Andreï Andreïevich Markov ont montré en 1947, que tout calcul peut se mener par des transformations sur des mots.
Dans un monde dominé par les machines (de Turing) et par les parpaings (de Scratch), les mots n’ont pas dit leur dernier mot.
Article placé sous licence CC-by-SA : http://creativecommons.org/licenses/by-sa/3.0/fr/legalcode
NB : pour programmer Toto le robot, on peut utiliser une version Scratch, et la remixer pour se l’approprier.
Mais dans l’esprit de cet article, et pour écrire des programmes qui écrivent des programmes intéressants, il est recommandé d’utiliser les scripts de l’article, en Python ou en Javascript (via CaRMetal).
Pour s’adresser à Toto le robot, on lui donne un mot plus ou moins long écrit avec les lettres A, R, G D.
On peut alors s’intéresser :
- à la variation finale de position et d’orientation du robot ;
- à son parcours (matérialisé par une trace).
Initialement, on considère que Toto est orienté vers l’Est.
Après avoir entendu le mot GADADAGA :
- Toto se retrouve +2 vers l’Est avec la même orientation ;
- a réalisé le parcours suivant :

On peut alors donner rapidement des exercices de nature « littéraire » :
- Quel est le mot (minimal) ayant donné le tracé ci-contre ?

- Peut-on caractériser les mots donnant des polygones fermés ?
Dans ce contexte, un mot est un programme valide et réciproquement.
Ecrire un programme, c’est écrire un mot. La question devient de savoir comment on va générer ce mot.
Dans cet article, on va voir comment on peut générer ce mot par différents systèmes de réécriture (ces systèmes de réécriture seront mis en œuvre en pratique par un programme d’une autre nature, en Python ou dans le langage de CaRMetal, c’est-à-dire en JavaScript).
Mise en œuvre et premier exemple
Mise en œuvre : compilation
En pratique, on va simuler les programmes de Toto avec un programme en Python (langage) ou dans le langage de CaRMetal (en Javascript) . En effet ces deux environnements proposent une « tortue » (robot virtuel représenté par un quadrilatère sur les copies d’écran ci-dessus) qui est capable de dessiner la trace du parcours. Il s’agit ici de concevoir un compilateur qui sera utilisé par tous les programmes que l’on générera.
Pour se faciliter la programmation sur les mots, on utilise aussi un ensemble de procédures spécialisées dans la recherche et la transformation des mots inscrits à l’intérieur d’autres mots : une expression régulière [4].
Le compilateur va
- traduire dans l’autre langage le programme initialement écrit en langage RAGD de Toto le robot ;
- puis exécuter le programme obtenu.
exemple : dragon par pliage
La tortue, le python et le dragon
On va voir ici l’exemple d’une transformation de mot assez singulière. A priori cette méthode n’entre dans aucune des trois catégories que l’on verra plus bas.
Mais le mot qu’elle génère pourra, lui, être généré par un L-système (autrement dit par un procédé entrant dans une des trois catégories).
La suite de pliage de papier est une suite binaire :
- Initialement le programme est un mot binaire composé du seul chiffre « 0 » (les chiffres, rappelons-le, sont des lettres, les mots écrits à l’aide d’eux représentant des nombres) ;
- à chaque transformation, on modifie ce programme pour qu’il représente les débuts successifs du mot binaire appelé « suite de pliage de papier » ou « suite du dragon » (voir ci-dessous pourquoi) : C’est un mot binaire (une suite de « 0 » et de « 1 ») de plus en plus compliqué ;
- Ensuite on traduit ce programme en un programme pour Toto le robot, en remplaçant chaque « 0 » par « GA » et chaque « 1 » par « DA » ;
- Enfin le compilateur traduit ce programme géant en un programme, qui permet à la tortue de dessiner la courbe du dragon : On dirait une légende chinoise...
Le plus long c’est la construction, par transformations successives, du mot binaire :
- Le mot binaire actuel est le préfixe du prochain mot ; on va juste lui rajouter un « 0 » et un suffixe ; pour ce suffixe, on copie le mot lui-même puis
- on remplace chaque « 0 », provisoirement, par un « Z » (parce qu’à l’étape suivante on va créer des « 0 » qui ne doivent pas être transformés à cette étape) ;
- puis on remplace chaque « 1 » par un « 0 » ;
- et chaque « Z » (ancien « 0 ») par un « 1 » ;
- enfin on ajoute à droite le mot inversé.
En fait, la lettre « Z » joue le rôle d’une variable temporaire permettant d’échanger les « 0 » et les « 1 ». Par exemple, « 1010 » devient successivement « 1Z1Z » puis « 0Z0Z » puis « 0101 ».
On notera que pour cette méthode, comme on ne s’est pas assujetti à un cadre précis, la lettre « Z » pourrait être évitée en décrivant le processus en langage naturel (ou en utilisant une fonction récursive).
Une version DGPad (qui ne fait pas explicitement appel à un système de réécriture) est ici.
patron développable
Dans son formidable article sur la tortue dynamique de DGPad, Yves Martin, après avoir donné de nombreux exemples, lance l’idée de systématiser et de formaliser des méthodes pour le développement de patrons en repère mobile.
Le travail que l’on va faire dans cet onglet sur un patron de cube, bien que ciblé, s’inscrit dans cette problématique.
On souhaite donc réaliser le développement générique d’un patron de cube. Et on va raisonner sur le patron suivant :

Ce patron est fléché, on verra pourquoi plus loin.
On part d’une figure CaRMetal 3D dans laquelle on a construit :
- un point 3D nommé B ;
- un curseur c entre 0 et 90° (pour le développement du patron).
On commence par enrichir le compilateur :
fonction Toto(x) {
x=x.replace(/A/g,"Avancer(1);");
x=x.replace(/R/g,"Reculer(1);");
x=x.replace(/D/g,"TournerDroite(90);");
x=x.replace(/G/g,"TournerGauche(90);");
x=x.replace(/P/g,"PivoterDroite(\"c\");");
x=x.replace(/Q/g,"PivoterGauche(\"c\");");
x=x.replace(/C/g,"for (var i=0;i<4;i++) {Avancer(1);TournerGauche(90);}Avancer(1);");
x=x.replace(/E/g,"for (var j=0;i<4;j++) {Avancer(1);TournerDroite(90);}Avancer(1);");
eval(x);
}On voit que l’on a ajouté quatre lettres à l’alphabet :
- P et Q pour Pivoter à droite ou à gauche d’un angle c ;
- C et E pour faire un carré, soit vers la droite, soit vers la gauche + un déplacement Avancer
Comme indiqué sur le patron annoté plus haut, on va replier le patron sur la face 1, considérée comme fixe.
On commence par le carré 1 :
Pour un carré tout bête vers la droite, on aurait :
ruban = "ADADADAD";Mais certains A sont remplacés par C ou par Y. On écrit donc :
ruban = "ADCDYDCD";C et Y sont développables, donc on poursuit avec :
ruban=ruban.replace(/C/g,"PCQ");
ruban=ruban.replace(/Y/,"PC'Q");Pour les deux C, c’est fini. On poursuit avec C’ :
Il faut faire un carré vers la gauche (mais un A sera remplacé par E’) + A
On ajoute :
ruban=ruban.replace(/C'/,"AGAGE'GAGA");Mais E’ doit pivoter. On ajoute :
ruban=ruban.replace(/E'/,"QE'P");E’, c’est un carré vers la droite, avec un A remplacé par C’.
On termine donc par :
ruban=ruban.replace(/E'/,"ADADCDADA");
ruban=ruban.replace(/C/,"PCQ");On n’a plus qu’à compiler ce ruban pour obtenir le développement du patron.
En lançant le script, on obtient la figure suivante :

La tortue de CaRMetal étant mutante, les éléments construits par la tortue peuvent être utilisés pour compléter la figure. On peut par exemple colorier les faces en créant des polygones à partir des sommets.
Et voici le classeur CaRMetal :
L-systèmes
Dans un L-système, on a un alphabet et des règles de réécriture qui, à chaque étape, s’appliquent l’une après l’autre à toutes les occurrences d’une lettre :
- certaines lettres (les graines) germent [6] ;
- d’autres (les constantes) stagnent.
Exemples de la théorie de la petite graine :
Flocon fractal
Dans ce premier onglet, on utilise uniquement notre alphabet de quatre lettres.
La transformation de textes, appliquée à un programme dans le langage RAGD de Toto le robot, permet de dessiner des courbes fractales : à partir d’un mot du langage RAGD on génère un autre mot du langage RAGD, et ce dernier mot constituera le programme qui sera exécuté par le compilateur.
L’idée est de partir d’un programme d’une seule lettre : A, qu’on va considérer comme une graine qui va germer. Pour simuler la croissance de cette graine, on va effectuer une substitution : remplacer chaque A (au début il n’y en a qu’un seul) par AGADADAAGAGADA qui dessine un côté du flocon :

Puis on recommence avec le nouveau mot obtenu...
dragon par L-système
La courbe du dragon, ou fractale du dragon, est, comme son nom l’indique, de nature fractale. Ce n’était pas acquis d’avance si l’on s’en réfère très rapidement à sa génération par pliage, mais c’est bien le cas. Et on peut la construire par un L-système.
Pour adapter le fichier précédent et en faire un L-système, on ajoute deux symboles a (variante de 0) et b (variante de 1).
Le système de règles est :
_0 → 0a
a → 1a
1 → 0b
b → 1b
Et on part de 0. C’est un point de départ classique mais raisonnable.
Voici un classeur CaRMetal avec les deux versions :
Et une sortie d’écran obtenue avec CaRMetal :

substitution
On peut remarquer que cette transformation de mots dans les L-systèmes (c’est la plus naturelle) fonctionne comme celle du calcul formel : Calculer l’image de 2 par l’homographie $\frac{x+5}{x+3}$ c’est remplacer ("substituer") chaque occurence de la lettre x par 2, pour obtenir $\frac{2+5}{2+3}$ soit 1,4..
D’autres exemples importants apparaissent en cryptographie (qui consiste à substituer à chaque lettre, une autre lettre), en conjugaison (on substitue à la terminaison « er » de l’infinitif, une autre terminaison comme « es » à la seconde personne), et même en génétique, la transcription (biologie) étant une forme de substitution de mots écrits dans le langage génétique...
Mais l’exemple ci-dessus mène au lambda-calcul : Si, au lieu de remplacer les « x » par des « 2 », on remplace les « x » par des « t », on ne change pas la nature du problème ; par exemple la fonction est toujours homographique, c’est juste le nom de la variable qui a changé. Cette règle de réécriture, appelée α-conversion, est considérée comme la base du lambda-calcul. Plus bas on abordera un outil de modélisation du lambda-calcul par des réécritures explicites : La logique combinatoire de Curry. Mais d’abord, d’autres systèmes de calcul par réécriture, bien qu’historiquement ultérieurs, seront abordés : Celui de Markov et celui de Post.
Exercice
Près de la fontaine de Perlin dans la forêt de Main-Molle, se trouve cet antique monument ; saurez-vous le reproduire avec un L-système ?

Aide : La version Python, avec une seule étape, et la tortue visible à la fin :

Et la version CaRMetal :

En fait, ce monument de la fontaine de Perlin est situé dans un univers tridimensionnel (la fontaine est derrière le monument) et végétal (la forêt de Main-Molle). Et la végétation qui l’envahit est elle-même générée par des L-systèmes.
Dans l’espace, la tortue 3D de CaRMetal peut tricoter des trajectoires qui rendraient fous tous les hélicoptères.
Espace
Mutant turtles from outer space
La version CaRMetal présente l’avantage sur la version Python de fonctionner aussi en 3D et on peut envisager des instructions supplémentaires :
- H qui fait tourner la tortue de 90° vers le haut ;
- B qui la fait tourner vers le bas de 90° ;
Perlin
Dans CaRMetal, la tortue est attachée à un point. Si ce point est un point 3D, on peut dessiner le L-système dans un plan horizontal. Il suffit de remplacer Point par Point3D :
fonction toto(x) {
x=x.replace(/A/g,"Avancer(0.125);");
x=x.replace(/R/g,"Reculer(0.125);");
x=x.replace(/D/g,"TournerDroite(90);");
x=x.replace(/G/g,"TournerGauche(90);");
eval(x);
}
B=Point3D("B",1,1,1);
AttacherTortue(B);
programme="A";
for (i=0; i<3; i++){ programme=programme.replace(/A/g,"AGADADAGA");
}
toto(programme);L’effet est saisissant :

Une petite modification de cette grammaire permet de dessiner le réseau de lierre qui entoure le monument.
Lierre
Voici la transformation proposée :
« A » → « AHABGADADAGBAHA »
Voici le lierre de la forêt de Main-Molle :

Vu de face, ce lierre a l’air aussi énigmatique que le pagicien Perlin en personne :

Mais vu d’avion, pardon !

Voici un lierre plus tropical (il pousse un peu dans toutes les directions) :
« A » → « AHADABADAGAGBADA »
moulin
Le programme suivant fait dessiner par la tortue 3D de CaRMetal, un moulin avec son axe :
« AHABABABADADADAHADADADABABABAGBAA »
La version L-système donne donc une courbe fractale un peu trop dense pour qu’on puisse y voir en perspective. La voici toutefois :
Mais cette variante rapetisse les ailettes par rapport à l’axe :
« AAHABABABADADADAHADADADABABABAGBAAA »
(à chaque fois ce sont les « A » qui sont remplacés par ces trajets)
Voici la vue en perspective du moulin de Perlin (qui est alimenté par l’eau de la fontaine, contrairement à Perlin lui-même, dont la légende dit qu’il ne boit pas que de l’eau de sa fontaine...) :

Vu de face :

Et vu d’avion :

En fait ce n’est pas le moulin de Perlin, c’est le moulin du poulain de Perlin...
L’un des intérêts des systèmes de Lindenmayer vus ci-dessus est qu’ils ont une interprétation graphique attractive : les courbes fractales. Mais on peut aussi s’intéresser aux mots eux-mêmes et faire des calculs avec ces mots, soit en fabriquant des phrases comme le fait Chomsky, soit en codant des nombres par des mots.
En fait, certains types de grammaires transformationnelles sont suffisamment éloquentes pour simuler n’importe quelle fonction calculable, comme l’a montré Markov dans les années 1950. On va plus bas s’intéresser particulièrement à trois de ces types de grammaires éloquentes :
- les algorithmes de Markov
- les tag-systèmes
- La logique combinatoire.
Algorithmes de Markov
Introduction : Thue
Si l’on s’intéresse exclusivement à la position et la direction finale de la tortue, et pas à la trace laissée par la tortue, le langage de programmation de Toto le robot a une particularité qui n’a aucune raison d’être universellement répandue parmi les langages de programmation : toute instruction a une inverse ; plus précisément :
- l’inverse de « A » (avancer) est « R » (reculer), puisque « AR » et « RA » font revenir le robot à sa position initiale ;
- l’inverse de « G » (gauche) est « D » (droite) puisque « GD » et « DG » font revenir Toto à son orientation initiale.
semi-Thue
Les langages de programmation étudiés étant des semi-groupes, Post a qualifié de « semi-thuéiens » les systèmes de réécriture. Ceux-ci sont constitués d’une chaîne de caractères dont on modifie répétitivement un morceau à l’aide de règles de transformation (qui disent par quoi on doit remplacer le sous-mot) jusqu’à l’obtention d’une condition d’arrêt (par exemple, quand on ne trouve plus de règle de transformation à appliquer, on a fini). Le fait qu’il y a plusieurs règles de transformation et plusieurs endroits où on peut en appliquer une donnent un caractère non déterministe à ces systèmes de réécriture. Pour les rendre déterministes, il y a plusieurs façons de s’y prendre :
- Aristid Lindenmayer (L-systèmes comme on l’a vu plus haut) propose d’appliquer toutes les règles partout où c’est possible.
- Markov propose un ordre d’application des règles (voir onglet suivant) ;
- Post propose d’appliquer l’unique règle possible au début du mot et d’opérer par suffixe (« tag system »)(voir le bloc d’onglets suivant).
Markov
Le principe d’un algorithme de Markov est le suivant :
- on parcourt les clés qui sont des sous-mots possibles du mot à transformer ;
- au premier sous-mot qui est dans le mot, on cesse de boucler : On a trouvé une transformation à effectuer ;
- on remplace alors la première occurence du sous-mot par la valeur de même numéro que la clé : C’est la transformation de chaîne de caractères constituant un pas de l’algorithme de Markov.
- On recommence tout jusqu’à la disparition d’un caractère « non terminal » (qui veut dire qu’on n’a pas terminé ; Chomsky utilise les majuscules pour dénoter les caractères non terminaux ; Markov utilise le point comme caractère terminal).
La chaîne de caractères s’apelle ici ruban. En effet elle modélise le ruban d’une machine de Turing. C’est d’ailleurs en traduisant les instructions d’une machine de Turing, en transformations de texte, que Post et Markov ont démontré l’universalité de ce genre de modèle de calcul.
Comme on s’arrête de boucler dès qu’on a trouvé un sous-mot dans les clés, on utilise l’instruction break de Python. Sinon on boucle sur les indices possibles dans la liste cles des précédents des règles de transformation (il y a autant de conséquents dans valeurs que de précédents dans cles puisqu’à chaque clé correspond une unique valeur). Pour savoir combien il y a d’entrées dans la liste des cles on utilise len(cles). Donc on fait un break dès que cles[n] in ruban.
Si la lettre non terminale est « P » (comme « plus »), le script est le suivant :
# -*- coding: utf8 -*-
from re import *
while "P" in ruban:
for n in range(len(cles)):
if cles[n] in ruban:
break
ruban = sub(cles[n],valeurs[n],ruban)
print rubanComme premier exemple, on va utiliser une seule règle de transformation : Enlever la lettre « P » qui n’a été placée qu’une seule fois dans le ruban. Pour cela on remplace le sous-mot « P » par du rien, et sinon, le sous-mot vide par lui-même (autrement dit on ne fait plus rien, ce qui veut dire qu’on a fini : On peut aussi prendre ça comme test de terminaison). Ce qui s’écrit
- « P » → « »
- « » → « »
Dans la suite, on n’écrira pas les guillemets ni la dernière règle de transformation. Ces deux règles sont programmées en Python par ces deux listes :
cles = ["P",""]
valeurs = ["",""]Pour faire fonctionner cet algorithme de Markov, il suffit de définir une valeur de départ pour le ruban : On va programmer une addition unaire, en posant par exemple l’addition 8+5 sous la forme de 8 pions, suivis de la lettre « P » et de 5 pions, comme ceci : ♟♟♟♟♟♟♟♟P♟♟♟♟♟
La création de cette chaîne de caractères peut se faire avec des multiplications en Python :
ruban = "♟"*8+"P"+"♟"*5L’avantage de la notation unaire, c’est qu’il suffit d’enlever le « P » pour avoir les 13 pions à la suite :
♟♟♟♟♟♟♟♟P♟♟♟♟♟
♟♟♟♟♟♟♟♟♟♟♟♟♟Des choses plus sérieuses seront présentées dans les onglets suivants.
PGCD
Pour la soustraction unaire, on utilise le fait que (a+1)-(b+1)=a-b, ce qui se modélise en enlevant toute paire de pions située de part et d’autre du « M » (comme « moins », utilisé à la place du « P » de l’onglet précédent). La grammaire transformationnelle utilisée pour ça est celle-ci :
- ♟M♟ → M
- ♟M → ♟
La première règle effectue la soustraction étape par étape, et on a fini lorsque le « M » n’est plus suivi par un ♟ : On est arrivé à une différence du type n-0, alors on applique la seconde règle qui enlève simplement la lettre non terminale pour signifier qu’on a terminé.
L’algorithme d’Euclide permet, à l’aide de soustractions itérées, de calculer un pgcd en unaire. On a besoin de plusieurs symboles non terminaux : A, B, C et le symbole G qui désigne l’opération de PGCD (G comme pGcd...). Les règles sont les suivantes :
- ♟A → A♟
- ♟G♟ → AG
- ♟G → GB
- B → ♟
- A → C
- C → ♟
- G♟ → ♟
On les représente, ainsi que l’opération de pgcd à calculer (celui de 8 et 6), par ce script :
cles = ["♟A","♟G♟","♟G","B","A","C","G♟",""]
valeurs = ["A♟","AG","GB","♟","C","♟","♟",""]
ruban = "♟"*8+"G"+"♟"*6La soustraction s’effectue comme ci-dessus mais en même temps, on remplace les pions de gauche par des « A » et ceux de droite par des « B ». Ensuite, via des « C » pour les pions de gauche, on réécrit les pions à la place des « A » (enfin, des « C ») et des « B ». Puis on recommence. Les étapes avec des pions sont les suivantes :
- ♟♟♟♟♟♟♟♟G♟♟♟♟♟♟
- ♟♟♟♟♟♟G♟♟ (le pgcd de 8 et 6 est le pgcd de 6 et 2)
- ♟♟G♟♟♟♟ (c’est aussi le pgcd de 2 et 4)
- ♟♟
et effectivement le pgcd de 8 et 6 est bien 2.
Multiplication
Cette grammaire transformationnelle effectue une multiplication unaire, en écrivant le symbole « M » (de multiplication) entre deux suites de pions, elle produit in fine un ensemble de pions dont le cardinal est le produit de ceux des deux « facteurs » :
- B♟ → ♟B
- A♟ → ♟BA
- A →
- ♟M → MA
- M♟ → M
- M →
- B → ♟
binaire
La conversion de binaire (écrit avec les lettres « 0 » et « 1 ») vers unaire (écrit avec des pions) se fait avec ces trois règles de transformation :
- ♟0 → 0♟♟
- 1 → 0♟
- 0♟ → ♟
En Python :
cles = ["♟0","1","0♟",""]
valeurs = ["0♟♟","0♟","♟",""]
ruban = "10101"Cette fois-ci il y a deux symboles non terminaux : « 0 » et « 1 ». Donc on continue à boucler tant que « 0 » in ruban or « 1 » in ruban. Avec le nombre 21 qui en binaire s’écrit « 10101 », on a les sorties suivantes :
10101
0♟0101
00♟♟101
00♟♟0♟01
00♟0♟♟♟01
000♟♟♟♟♟01
000♟♟♟♟0♟♟1
000♟♟♟0♟♟♟♟1
000♟♟0♟♟♟♟♟♟1
000♟0♟♟♟♟♟♟♟♟1
0000♟♟♟♟♟♟♟♟♟♟1
0000♟♟♟♟♟♟♟♟♟♟0♟
0000♟♟♟♟♟♟♟♟♟0♟♟♟
0000♟♟♟♟♟♟♟♟0♟♟♟♟♟
0000♟♟♟♟♟♟♟0♟♟♟♟♟♟♟
0000♟♟♟♟♟♟0♟♟♟♟♟♟♟♟♟
0000♟♟♟♟♟0♟♟♟♟♟♟♟♟♟♟♟
0000♟♟♟♟0♟♟♟♟♟♟♟♟♟♟♟♟♟
0000♟♟♟0♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟
0000♟♟0♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟
0000♟0♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟
00000♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟
0000♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟
000♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟
00♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟
0♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟
♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟♟On peut compter les pions, il y en a bien 21 !
Envers
Cette grammaire écrit un mot binaire à l’envers, par exemple 11010 devient 01011 :
- AA → B
- B0 → 0B
- B1 → 1B
- BA → B
- B →
- A00 → 0A0
- A01 → 1A0
- A10 → 0A1
- A11 → 1A1
- → A
La condition d’arrêt est l’absence de lettres non terminales (« A » ou « B ») du ruban. Cette condition est déjà atteinte dès le début, il faut donc faire tourner la boucle une fois avant de tester la condition d’arrêt. Avec 01101 au départ, voici la suite des états successifs du ruban :
01101
A01101
1A0101
11A001
110A01
1101A0
A1101A0
1A101A0
10A11A0
101A1A0
A101A1A0
0A11A1A0
01A1A1A0
A01A1A1A0
1A0A1A1A0
A1A0A1A1A0
AA1A0A1A1A0
B1A0A1A1A0
1BA0A1A1A0
1B0A1A1A0
10BA1A1A0
10B1A1A0
101BA1A0
101B1A0
1011BA0
1011B0
10110B
10110À titre de comparaison, voici comment on peut programmer cet algorithme avec Sofus :

L’idée est de considérer la chaîne de caractères « entree » comme génératrice d’une boucle (en bouclant sur le numéro de la lettre) ; pour peu qu’on boucle en commençant par la fin, on construit, lettre par lettre, le même mot mais à l’envers. Sofus est un outil d’ajout de suffixes, et sera donc plus adapté aux « tag-systems » de Post que l’on verra plus bas.
incrémentation
Cette grammaire transformationnelle incrémente un nombre écrit en binaire, du moment qu’au départ celui-ci est entre deux caractères « underscore » :
- 1_ → 1pp
- 0_ → 1
- 01pp → 10
- 11pp → 1pp0
- _0 → _
- _1pp → 10
En fait le calcul est souvent très court : Par exemple pour vérifier que 11+1=12, on a juste
_1011_
_1011pp
_101pp0
_1100Et pour calculer 255+1 :
_11111111_
_11111111pp
_1111111pp0
_111111pp00
_11111pp000
_1111pp0000
_111pp00000
_11pp000000
_1pp0000000
100000000Un décrémenteur binaire n’est guère plus complexe à programmer :
- 0_ → 0mm
- 1_ → 0
- 10mm → 01
- 00mm → 0mm1
- _1mm → @
- _0mm → 1
Par exemple pour vérifier que 8-1=7 :
_1000_
_1000mm
_100mm1
_10mm11
_0111Un autre modèle de calculabilité par les mots a été développé avant Markov, par Emil Post : Les « tag systems » :
Tag-systems
Attrape
Au Québec, le jeu de chat perché s’appelle tague : Le « chat » est « la tague », et aux États-Unis, les jeux de type « attrape » sont appelés « tag games ». C’est à ce jeu que faisait allusion Emil Post lorsqu’il a inventé ce modèle de calculabilité simulant une file (structure de données) : Lors de la simulation, le pointeur de lecture avance à vitesse constante et le pointeur d’écriture avance à vitesse variable, une question assez naturelle étant de savoir si le premier arrivera à rattraper le second à un moment donné, d’où l’analogie avec « chat perché » : Le pointeur de lecture court après le pointeur d’écriture.

Réussira-t-il à le rattraper ? Emil Post dit : « La question est indécidable ».
Efficacité
Pour simuler un système de Markov, on doit effectuer à chaque passage dans la boucle, deux recherches :
- une recherche dans la grammaire, parmi les précédents (les sous-mots à transformer ou à « réécrire ») : Recherche courte parce que la grammaire est en général assez petite (peu de règles de transformation) ;
- une recherche, pour chacun des sous-mots de la grammaire, dans le mot ; pour voir si le sous-mot y est ; cette recherche est menée a priori plusieurs fois puisqu’il y a plusieurs règles de transformation dans la grammaire.
Et comme, au cours du calcul, la longueur du mot s’allonge arbitrairement, cette recherche risque d’être longue, même si elle s’arrête au premier sous-mot trouvé [9].
Dans un système de Post, au contraire, on ne cherche pas de sous-mot puisque c’est seule la lettre du début actuel du mot qui détermine la transformation à effectuer. En Python, cette lettre se note mot[0] ou mot[:1]. En plus il n’y a pas de recherche à effectuer pour modifier le mot puisque le sous-mot à insérer, est rajouté à la fin du mot actuel. Ce rajout, en Python, se note += de sorte que mot += suffixe a pour effet de modifier le mot par rajout du suffixe.
C’est sans doute cette efficacité algorithmique qui explique le fait que les systèmes de Post ont eu plus de succès que ceux de Markov dans la recherche en informatique théorique.
Post appelle ce genre de systèmes de réécriture des « systèmes normaux » : Ce sont ceux où la modification du mot se fait par ajout d’un suffixe et suppression d’un préfixe, et où le suffixe ne dépend que du préfixe. L’ensemble des mots produits par un tel système « normal » ou « canonique » de Post est dit récursivement énumérable.
La complexité des systèmes de tague peut être mesurée par le nombre de caractères effacés au début du mot après chaque ajout de suffixe. Par exemple, si après l’ajout du suffixe on efface 6 lettres au début du mot, on parlera de 6-tag system.
Mémoire
La mémoire tampon permettant de simuler un système de tague est un bon modèle pour la mémoire de travail. Plus précisément :
- le début du mot est stocké dans la mémoire à court terme ;
- la grammaire (qui dit quel suffixe correspond au début du mot) est stockée dans la mémoire à long terme et plus précisément sous forme de mémoire procédurale (le savoir-faire plutôt que le savoir, à comparer avec la fourmi de Langton qui a très peu de savoir faire mais peut faire plein de choses grâce au savoir stocké et traité dans son environnement).
Or la théorie de la charge cognitive affirme que la mémoire de travail est limitée ce qui induit des erreurs en cas de « surcharge cognitive » (lorsque le nombre d’éléments de mémoire sollicités devient supérieur au nombre d’éléments disponibles). C’est ce qui explique par exemple qu’une triple négation soient souvent interprétée comme une double négation.
Avec un 3-tag system, la mémoire de travail comprend 3 éléments en tout et pour tout. La théorie de Post permet donc de quantifier la notion de charge cognitive et peut donc être considérée comme une aide à la modélisation en sciences de l’éducation. Il est d’ailleurs significatif que les principaux promoteurs de ces systèmes de Post aient été des chercheurs en intelligence artificielle comme Marvin Minsky et Seymour Papert, d’ailleurs tous deux récemment disparus...
1-tag
On vu dans l’onglet « efficacité » comment un 1-tag system peut être utilisé pour calculer les termes successifs d’une suite géométrique. D’autres exemples de suites tant arithmétiques que géométriques sont montrés en bas de cet article. Ce sont des systèmes de Post qui ne s’arrêtent jamais mais qui, à certains moments (par exemple lorsque la lettre qui sert de marqueur se trouve au début du mot), donnent les termes successifs d’une suite d’entiers. On peut faire pas mal de choses avec un alphabet de deux lettres :
- l’une (ici le « o » qui évoque une petite bille ou « calcul ») permettant de représenter des entiers naturels dans le système unaire ;
- l’autre (ici « ! ») représentant un marqueur distinguant les valeurs remarquables du mot (lorsque le marqueur est au début du mot par exemple).
Or ce marqueur donne une condition d’arrêt permettant (par exemple lors d’une position particulière du marqueur) de terminer le calcul.
L’exemple de la suite géométrique vu à l’onglet « efficacité » peut donc facilement être modifié pour une fonction qui triple le nombre de billes « o » dans un nombre unaire formé de 7 « o » par exemple :
from re import *
regles = { "o": "ooo",
"!": "!"
}
ruban = "o"*7+"!"
while ruban[0] != "!":
print ruban
ruban += regles[ruban[0]]
ruban = ruban[1:]
print ruban
ruban = sub("!","",ruban)
print len(ruban)La sortie est très similaire à celle de la suite géométrique mais en n’en calculant qu’un seul terme :
ooooooo!
oooooo!ooo
ooooo!oooooo
oooo!ooooooooo
ooo!oooooooooooo
oo!ooooooooooooooo
o!oooooooooooooooooo
!oooooooooooooooooooooPour effectuer une division entière, on fait en quelque sorte l’inverse, soit en n’ajoutant qu’une seule bille à la fin au lieu de 3, et en enlevant 3 billes à chaque fois au début. On obtient alors un 3-tag système.
Voici comment on peut faire une addition unaire avec un 1-tag système de Post :
Marqueur : « P » comme « plus » ; le calcul est fini lorsque le marqueur est tout à gauche. Règles de transformation :
- « o » → « o » (la bille le plus à gauche est transférée à la fin)
- « P » → « » (lorsque le marqueur est tout à gauche, on l’enlève et son absence signifie la fin du calcul).
Le script en Python, avec condition de fin de boucle, est celui-ci (ici, pour calculer 8+5) :
from re import *
regles = { "o": "o",
"P": ""
}
ruban = "o"*8+"P"+"o"*5
while "P" in ruban:
print ruban
ruban += regles[ruban[0]]
ruban = ruban[1:]
print len(ruban)Les états successifs du ruban montrent que tout ce qu’on a fait est décaler le marqueur « P » vers la gauche pour l’effacer :
ooooooooPooooo
oooooooPoooooo
ooooooPooooooo
oooooPoooooooo
ooooPooooooooo
oooPoooooooooo
ooPooooooooooo
oPoooooooooooo
Pooooooooooooo
oooooooooooooet il y a bien 13 billes à la fin.
2-tag
Voici un algorithme de recherche de parité du nombre de billes « o », les billes étant initialement suivies de « PI » (comme « pair-impair ») : La grammaire transformationnelle est celle-ci :
- « o » → « »
- « P » → « pair »
- « I » → « impair »
La première règle a pour effet d’enlever les billes par paires : Il s’agit d’un 2-tag système où on enlève, à chaque passage dans la boucle, les deux premières lettres. Alors de deux choses l’une :
- ou bien il y a un nombre pair de billes et l’histoire se termine par « PI » qui commence par « P » comme « pair » ;
- où il y a un nombre impair de billes et on arrive à « oPI » qui donne « I » seulement : Dans ce cas la première lettre du mot est « I » comme « impair ».
Voici le codage en Python (remarquer que la dernière ligne est ruban = ruban[2 :] ce qui caractérise un 2-tag système) :
from re import *
regles = { "o": "",
"P": "pair",
"I": "impair"
}
ruban = "o"*21+"PI"
while "o" in ruban:
print ruban
ruban += regles[ruban[0]]
ruban = ruban[2:]
print regles[ruban[0]]Avec 21 au départ (qui est impair) on a ces sorties :
oooooooooooooooooooooPI
oooooooooooooooooooPI
oooooooooooooooooPI
oooooooooooooooPI
oooooooooooooPI
oooooooooooPI
oooooooooPI
oooooooPI
oooooPI
oooPI
oPI
impairAlors qu’avec 20 qui est pair :
ooooooooooooooooooooPI
ooooooooooooooooooPI
ooooooooooooooooPI
ooooooooooooooPI
ooooooooooooPI
ooooooooooPI
ooooooooPI
ooooooPI
ooooPI
ooPI
pairDeux idées sont importantes sur les 2-tags systèmes :
- Comme c’est un 2-tag système, on efface la seconde lettre avec la première et chaque instruction peut donc être codée sur deux lettres puisque la seconde lettre n’est pas lue [10] ;
- la parité peut être détectée par un tel 2-tag système. Mais aussi modifiée si le suffixe est impair.
La combinaison de ces deux idées a permis à Hao Wang, en 1963, de simuler une machine de Turing quelconque avec un 2-tag système, démontrant ainsi l’universalité de ces systèmes :
Pour toute fonction calculable, il existe un 2-tag système qui la calcule
Cependant, l’encodage des machines de Turing dans les 2-tags systèmes est vite complexe et la programmation d’algorithmes classiques n’y est pas spécialement facile. Mais Wang a obtenu par cette universalité la première preuve d’indécidabilité par systèmes de réécriture de type « canonique de Post » [11].
Décimal
Voici un problème de type « rallye maths » qui jusqu’à présent semble inédit :
Pour transformer un nombre entier (par exemple 2016), on réalise les opérations suivantes :
- On élève son premier chiffre au cube (par exemple 2³=8) ;
- On rajoute les chiffres du cube après l’écriture du nombre (par exemple 20168) ;
- On enlève les deux premiers chiffres : Le transformé de 2016 est donc 168.
On transforme 2016 fois le nombre 2016. Combien obtient-on ?
Et en transformant 2017 fois le nombre 2017 ? Et quels sont les nombres qui ne donnent pas 88 à un moment ou un autre ?
Il s’agit bien d’un 2-tag système de Post, avec la grammaire transformationnelle suivante :
0 → 0
1 → 1
2 → 8
3 → 27
4 → 64
5 → 125
6 → 216
7 → 343
8 → 512
9 → 729
Pour constituer ce dictionnaire on peut faire ainsi :
from re import *
regles = {}
for n in range(10):
regles[str(n)] = str(n**3)
ruban = "2016"
for n in range(2016):
print ruban
ruban += regles[ruban[0]]
ruban = ruban[2:]On peut généraliser par exemple avec les carrés (un 1-tag système convient alors mieux) ou les puissances quatrièmes etc.
Avec DGPad, on peut explorer dynamiquement les différents paramètres (entrée, nombre d’itérations de la règle, n-tag, puissance) :
Il suffit de créer une expression qui donne le résultat en fonction des différents paramètres. Voici le code de cette expression :
var aa=a;
var litt, nl, na, alapuisssance;
for (var j=0; j<b; j++) {
litt=aa.toString();
na=parseInt(litt.charAt(0));
alapuisssance=Math.pow(na,f);
nl=litt.substring(e);
nl+=alapuisssance.toString();
aa=parseInt(nl); };
aaCollatz
En 2008, Liesbeth DeMol a trouvé comment, avec un alphabet de seulement trois lettres (donc trois règles de transformation), on pouvait simuler la suite de Lothar Collatz avec un 2-tag système de Post :
La conjecture de Syracuse est intéressante dans le contexte de la calculabilité, parce qu’elle est à l’origine du langage de programmation Fractran qui serait d’ailleurs intéressant à pratiquer en collège parce qu’il est basé sur les fractions ; et programmer en Fractran c’est faire des révisions, pas forcément superflues, sur les fractions...
Mais la conjecture de Syracuse a été émise par Lothar Collatz en 1937 (c’est-à-dire une bonne vingtaine d’années avant sa formulation à l’université de Syracuse). Alors qu’une conjecture similaire, plus proche du problème du mot que de l’arithmétique, a été émise en 1921 par Emil Post. On la découvre dans l’onglet suivant parce qu’elle concerne un 3-tag système.
3-tag
16 ans avant l’invention de la suite de Collatz, Emil Post avait découvert ce système plus complexe puisque la période n’est pas toujours la même :
Alphabet « 0 », « 1 » (donc deux règles) :
- 0 → 00
- 1 → 1101
Le comportement de la suite semble totalement imprévisible et Post a émis la conjecture selon laquelle la question de savoir si elle est ultimement périodique, est indécidable. C’est en 2016 un problème ouvert. Dans le cas ci-dessus, on constate qu’après quelques errements, le système entre dans une période de longueur 6 :
Pour des mots initiaux de 12 lettres maximum, outre les mots menant à une extinction, tous les mots mènent en une trentaine d’étapes au plus, à une des ces périodes :
- période 2 (la plus fréquente) :
- 10100 (de deux mots, choisissons le moindre)
- 001101
- période 4 (la plus rare) :
- 1110100001101
- 01000011011101
- 0001101110100
- 110111010000
- période 6 (vue dans l’exemple ci-dessus) :
- 001101110111010000
- 10111011101000000
- 110111010000001101
- 1110100000011011101
- 01000000110111011101
- 0000011011101110100
Voici la représentation binaire (un pixel rouge pour « 1 » et un pixel bleu pour « 0 ») des 400 premières itérations à partir du mot « 100100100100100100100 » :

Aux grands mots, les grands remèdes !
Quelle est la période qui sera obtenue à la fin, et quand le système entrera-t-il dans cette période ?
Jeux
En parlant de jeux de mots, on imagine une histoire de ce genre :
L’inspecteur Langton cherche le mot « bile » dans un dictionnaire. Il perçoit le mot « tif » dans les éléments de son enquête. Il ouvre une fenêtre sur le mot « dalle ». Il a découvert le mot « hair » sur l’île de Pâques, et le mot « ka » et le mot « mie » en Égypte. Son assistant, qui lui sert du mot « Sieur » à bout de journée, a, à son grand désarroi, découvert le mot « lesté » hier soir. Son indic au surnom classique connaît bien le mot « mot » et fréquente le mot « rue ». En contemplant son reflet dans un sou, il découvre le mot « nez ». Lors de son dernier interrogatoire, il a crié « jeu de mots, jeu de vélo » ce que son assistant a qualifié de « méta-jeu de mot » !
Mais ce n’est pas à ce genre de jeu de mots qu’on pense ici. Plutôt au fait que si on parle depuis le début de cet article, de « règles » (de grammaire, de dérivation ou de transformation), on pense assez automatiquement à des « règles du jeu ». Quel jeu au fait ?
L’idée de départ est ce qu’on appelle les cyclic tags, où le suffixe n’est plus indexé par la première lettre du mot, mais par un entier automatiquement incrémenté modulo le nombre de règles.
L’idée des tags cycliques est d’utiliser une liste de suffixes, parcourue dans un ordre cyclique : On utilise la première règle, puis la seconde, puis la troisième, puis la première à nouveau etc. En n’imposant pas d’ordre de lecture des suffixes, on rend le système non déterministe, et on arrive à ce jeu à deux joueurs :
On considère un entier n (par exemple 2 pour un 2-tag), un mot initial (par exemple « 11001 » et une liste de suffixes possibles (par exemple [0, 1, 111]). Les joueurs, chacun son tour, choisissent et ajoutent au mot un suffixe de leur choix avant d’enlever les n premières lettres. Le joueur A gagne si le mot est vide, et le joueur B gagne s’il réussit à faire grandir indéfiniment le mot.
Il peut être intéressant de rajouter une règle interdisant l’utilisation d’une même règle deux fois de suite. Voici un exemple de début de partie :
- A joue 111 et obtient 11001111 puis 001111
- B joue 1 et obtient 0011111 puis 11111
- A joue 111 et obtient 11111111 puis 111111
- B joue 0 et obtient 1111110 puis 11110
- A joue 111 et obtient 11110111 puis 110111
- B joue 1 et ontient 1101111 puis 0111
- A joue 111 et obtient 0111111 puis 11111
Partie nulle puisqu’on est revenu à une phase du jeu déjà explorée.
Il peut être intéressant aussi de transformer ce jeu en un méta-jeu de Post en laissant les joueurs définir eux-mêmes les règles du jeu. Les enfants adorent ça.
Toto
On a vu plus haut que tout mot binaire peut se convertir en un programme pour Toto le robot, avec la correspondance
- « 0 » → « GA »
- « 1 » → « DA »
Cette conversion permet de considérer le problème de Post comme une suite de programmes pour Toto, donc comme une suite de figures dessinées par le robot.
Par exemple, avec le mot « 10110 » (soit « DAGADADAGA » qui dessine une manivelle), on sait que le système de Post produit
101101101
1011011101
10111011101
110111011101
1110111011101
011101110100
1011101001101
11010011011101
100110111011101
1101110111011101
11101110111011101
0111011101110100
10111011101001101
110111010011011101
1110100110111011101
010011011101110100
01101110111010000
0111011101000000
10111010000001101
110100000011011101En remplaçant chaque « 0 » par un « GA » et chaque « 1 » par un « DA », on a cette suite de mots :
DAGADADAGADADAGADA
DAGADADAGADADADAGADA
DAGADADADAGADADADAGADA
DADAGADADADAGADADADAGADA
DADADAGADADADAGADADADAGADA
GADADADAGADADADAGADAGAGA
DAGADADADAGADAGAGADADAGADA
DADAGADAGAGADADAGADADADAGADA
DAGAGADADAGADADADAGADADADAGADA
DADAGADADADAGADADADAGADADADAGADA
DADADAGADADADAGADADADAGADADADAGADA
GADADADAGADADADAGADADADAGADAGAGA
DAGADADADAGADADADAGADAGAGADADAGADA
DADAGADADADAGADAGAGADADAGADADADAGADA
DADADAGADAGAGADADAGADADADAGADADADAGADA
GADAGAGADADAGADADADAGADADADAGADAGAGA
GADADAGADADADAGADADADAGADAGAGAGAGA
GADADADAGADADADAGADAGAGAGAGAGAGA
DAGADADADAGADAGAGAGAGAGAGADADAGADA
DADAGADAGAGAGAGAGAGADADAGADADADAGADARemarque : Ce 6-tag système produit la même chose avec « DAGADADAGA » comme mot initial, et les règles suivantes :
- « G » → « GAGA »
- « D » → « DAGADADA »
La suite des dessins produits par ce système, une fois envoyés chaque seconde à Toto le robot, est celle-ci :

Aux 3 systèmes de réécriture (Lindenmayer, Markov et Post) vus ci-dessus, s’ajoute, historiquement parlant, la logique combinatoire, qui modélise le lambda-calcul par un système de réécriture. Mais ce sujet étant quelque peu plus ardu, on va maintenant s’octroyer deux moments de respiration, toujours en rapport avec l’étude mathématique des langages : Le langage d’un autre petit robot (la fourmi de Langton) et la programmation en Logo, qui est proche des attendus du programme de cycle 4 :
La tortue Logo est munie d’un crayon qui lui permet de dessiner. Mais un crayon, ça peut aussi servir à (ré)écrire. Voici un exemple de robot simplifié qui fait des dessins pixellisés, dessins qu’il est possible de considérer comme des mots binaires : Le robot lit et écrit sur son terrain, comme une termite construisant et aménageant une termitière : On l’appelle une turmite suite à une réécriture effectuée sur « Turing-termite » :
Langton
Dans les années 1980, Christopher Langton a trouvé un robot encore plus simple que Toto ; son programme est le suivant :
- Si la case lue par le robot est noire, le robot l’efface (ou la colorie en blanc) et se tourne vers la droite ;
- Sinon (c’est-à-dire si la case est blanche), le robot colorie la case en noir et se tourne vers la gauche.
- Dans les deux cas, le robot avance d’une case et recommence tout au départ.
La complexité des dessins produits par ce robot nécessite de zoomer de loin, et le robot semble alors à la fois petit et laborieux. Aussi l’appelle-t-on fourmi de Langton. Voici une simulation sur des cases initialement vides :

La fourmi de Langton est aussi programmable en Sc***ch...
Ce petit robot, au demeurant capable de calculer tout ce qui est calculable, permet d’aborder la combinatoire des mots avec la notion de mots infinis.
Mot
Dans ce fichier, le robot est représenté par une flèche rouge. Par exemple, ici il est sur une case blanche, et dirigé vers l’Est :

Il va donc colorier en noir le pixel sur lequel il se trouve et se tourner vers sa droite, c’est-à-dire, ici, vers le sud. En bref, on a choisi une convention différente de celle de l’onglet précédent.
Ici la fourmi est sur une case noire (il faut bien regarder pour la voir) et dirigée vers le Sud :

Elle va donc effacer la case et se tourner vers sa gauche, c’est-à-dire, dans le cas présent, vers l’Est.
Le fichier précité permet d’observer la fourmi de Langton, avec affichage d’un « 1 » ou d’un « 0 » selon la couleur de la case où se trouve la fourmi, et de la suite des « 0 » et des « 1 » lus par la fourmi depuis l’époque où toutes les cases étaient blanches : Au cours de l’expérience, la fourmi construit, lettre par lettre, un mot infini.
Ici on voit la même chose, mais sans affichage de la fourmi. En décalant le curseur vers la gauche, on peut accélérer le robot :
Négation
Voici un négateur pour la fourmi calculatrice du Chili. Pour le charger, on peut simplement choisir « negation » dans le menu des exemples ; on obtient alors queque chose de ce genre :

Dans la ligne du haut, une seule case est actuellement coloriée. Elle représente un « vrai » logique, parce qu’elle est à gauche du rectangle encadré de jaune en haut. Les autres parties du « circuit » servent essentiellement à guider la fourmi vers la droite de la figure.
La fourmi passe par le haut du losange ainsi formé, et aboutit à ceci :

Comme on le voit, le rectangle jaune en bas n’a pas été modifié (puisque la fourmi n’est même pas passée par là). Il représente alors un niveau logique « faux », qui est la négation de la valeur « vrai » qui était codée en haut.
Si, au contraire, on positionne la case coloriée en haut sur la droite, ce qui représente un « faux » logique :

la fourmi va alors passer par la moité basse du « losange » et se retrouver à droite mais avec un effet de bord sur le bas :

Cette fois-ci il y a deux cases coloriées en bas, et l’une des deux représente un « vrai » logique. En, considérant ce circuit comme un moyen de transport de l’information depuis le rectangle jaune du haut, vers le rectangle jaune du bas, on voit que l’information, au cours du trajet, a été transformée :
- un « vrai » est devenu un « faux »
- un « faux » est devenu un « vrai ».
Le « circuit logique » ainsi programmé effectue une négation sur son entrée, ce qui est une forme de calcul : La fourmi de Langton peut calculer. Un autre exemple de calcul binaire est décrit dans l’onglet suivant.
Conjonction
Dans ce circuit, les deux rectangles en haut sont des entrées binaires, ici sur « 0 » (c’est la case de droite qui est coloriée) :

Du fait que l’entrée de gauche est sur « 0 », la fourmi fait un circuit en diagonale, depuis en haut à gauche vers en bas à droite, sans tenir compte de la valeur de l’entrée de droite (puisqu’elle ne passe pas par là, et finit le circuit à droite) :

N’étant pas passée par la sortie (rectangle jaune en bas à gauche), elle a laissé celle-ci à « 0 » et donc dans cette configuration, on a 0×x=0 quelle que soit la valeur de x.
Pour calculer 1×0, on positionne l’entrée de gauche à « 1 » et celle de droite à « 0 » :

Le fait que l’entrée de gauche soit à « 1 » dévie la trajectoire de la fourmi vers la seconde entrée ; et le fait que celle-ci soit à « 1 » la dévie ensuite directement vers la sortie :

N’étant pas passée par la sortie, la fourmi a laissé celle-ci à « 0 » ; donc on a 0×1=0. Reste à voir ce qui se passe avec 1×1, c’est-à-dire en positionnant à « 1 » les deux entrées :

Là encore, la fourmi est déviée par la première entrée, vers la seconde entrée. Elle va ensuite être déviée, parce que la seconde entrée est « 1 », vers la sortie, et fait une fin de tour en bas vers la droite, avant de sortir sur la droite. Ce faisant elle positionne la sortie sur « 1 » :

On a donc bien 1×1=1 et le circuit réalise une opération booléenne de conjonction (ou de multiplication). Dans cet article, Anahi Gajano et al montrent comment on peut créer d’autres circuits de calcul, avec des techniques qui permettent, en théorie, de faire mener par la fourmi de Langton, tout calcul qui peut se ramener à un calcul booléen.
Dans le cadre de cet article, ce sont des réécritures sur un mot infini...
Shift
Dans les itérations de fonctions vues sous l’angle des systèmes dynamiques, un outil concernant les mots infinis est très pratique : La dynamique symbolique. Dans le cas de la célèbre suite un+1=4un-4un2, on code le mot infini de cette façon :
- Si u0 est inférieur à 0,5 la première lettre du mot est 0, sinon c’est 1 ;
- On applique la fonction f(x)=4x-4x2 et on recommence : Si u1 est inférieur à 0,5 la seconde lettre est un 0, sinon c’est un 1 ;
- etc : Si un est inférieur à 0,5 la dernière lettre est un 0 sinon c’est un 1.
On démontre alors les faits suivants :
- Presque tout nombre entre 0 et 1 est codé par un unique mot binaire infini (les exceptions sont 0,5 et ses préimages) ;
- L’ensemble des mots binaires est muni d’une topologie : Celle de l’espace de Cantor ;
- Pour cette topologie, deux mots infinis sont proches s’ils représentent des nombres proches entre 0 et 1 ;
- L’équivalent de la fonction f(x)=4x-4x2 dans l’espace de Cantor est une fonction très simple : Celle du décalage (ou « shift ») , consistant à remplacer, dans le mot infini, chaque lettre par la lettre suivante.
Le shift est donc un équivalent, pour les nombres infinis, des 1-tag systèmes de Post. La dynamique symbolique est utile dans la théorie des systèmes dynamiques, parce qu’elle permet facilement de démontrer des faits comme l’existence de chaos. Par exemple, en étudiant un nombre correspondant à un mot sturmien, on obtient l’existence d’une orbite dense qui est indicatrice de chaos.
Pour explorer cette idée, voir l’onglet « suites » de cet article, qui comprend une figure CaRMetal permettant de voir « en live » le début du mot infini correspondant à un nombre initial (avec « G » au lieu de « 0 » et « D » au lieu de « 1 »)
Le chat d’Arnold est un bon exemple de dynamique symbolique sur des mots infinis non binaires : On a un point (en rouge ci-dessous) dans le carré formé des points dont l’abscisse et l’ordonnée sont toutes deux entre 0 et 1. Puis, en notant x et y les coordonnées de ce point, on ajoute à la figure (en bleu) le point dont les coordonnées sont les parties fractionnaires de x+y et x+2y . Puis on recommence, et encore, et encore, en tout 400 fois sur la figure DGPad ci-dessous :
En bougeant le point rouge sur la figure ci-dessus, on constate que le nuage de points bleus ainsi obtenu semble aléatoirement réparti dans tout le carré. Et il semble difficile de trouver une position du point rouge pour laquelle ce n’est pas le cas ;-)
Le fait que le nuage de points est équiréparti se démontre avec la dynamique symbolique. Mais alors que pour la fonction 4x-4x2, les lettres désignaient deux intervalles (à gauche de 0,5 ou à droite de 0,5), pour le chat d’Arnold il y a 6 « rectangles » (dessinés sur un tore, ce qui fait qu’ils ont l’air d’être en plusieurs morceaux) :

Ce dessin est fait pour une version transposée du chat d’Arnold (en échangeant les abscisses et les ordonnées). Une trajectoire du chat d’Arnold correspond donc à un mot infini sur un alphabet de 6 lettres puisqu’il y a 6 « rectangles » où peut se trouver le n-ième point. Et comme, si par exemple, si le point est dans w6 (en gris foncé), son transformé ne peut pas être dans w1 ni dans w2 (en blanc), on en déduit que le mot infini écrit sur l’alphabet 1-6 ne peut pas contenir certains sous-mots comme « 61 » ou « 62 ». On dit que ce système dynamique est de type fini parce que les sous-mots (wikipedia dit « facteurs ») évités forment un langage fini.
Il peut arriver que la situation soit plus complexe, et que les sous-mots évités forment un langage plus compliqué qu’un langage fini : Par exemple, on dit d’un système dynamique qu’il est sophique si les mots évités forment un langage régulier. Et bien, justement, c’est le cas pour la fourmi de Langton
Pour des exemples similaires, voir cet article.
Théorie du tout
Dans cet article, Ian Stewart utilise la fourmi de Langton pour illustrer le débat sur la théorie du tout : La recherche d’une équation unique modélisant tous les phénomènes de l’univers. Une telle équation serait mystérieuse parce qu’elle permettrait d’engendrer (par sa résolution) une complexité sans limite, donc sans commune mesure avec la simplicité de l’équation elle-même.
L’analogie avec la fourmi de Langton est évidente : La fourmi est un robot minimaliste et la complexité des motifs qu’elle dessine est impressionnante. Stewart utilise cette analogie pour parler d’indécidabilité : Bien que la fourmi soit parfaitement déterministe, il y a des questions (comme « finira-t-elle par dessiner une autoroute ? ») dont la réponse n’est pas connue à ce jour.
L’article de Stewart suggère une autre analogie : La fourmi de Langton est très simple et les données sur lesquelles elle travaille sont très complexes : La complexité réside plus dans les données que dans le programme. Pour l’équation du tout, on peut donc s’attendre à ce qu’elle ne prédise pas grand-chose parce que ses conditions initiales (les données) ne sont pas simplifiables même si l’équation est simple. Pour deviner ce que fait une fourmi de Langton à l’avance, rien de tel que de la laisser calculer et regarder. Autre manière de le dire : Une machine de Turing est finie mais son ruban (sa mémoire) est infini.
Il est prévisible que la fourmi de Langton soit encore étudiée dans les années qui viennent, car l’analogie ci-dessus pourrait bien s’appliquer à l’aspect « algorithmes dirigés par les données » des big data. Et les langages de programmation dirigés par les données, comme awk ou sed, pourraient bien avoir de l’avenir dans ces recherches.

Fourmilière
Si une fourmi de Langton peut communiquer avec elle-même par les dessins qu’elle fait sur le plan pixellisé, il est également possible de faire communiquer entre elles plusieurs fourmis de Langton qui cohabitent sur un même plan, chacune « écrivant » sur le plan dans une couleur, et lisant les « écrits » antérieurs des fourmis, elle-même et les autres.
Voici le genre de comportement qui émerge de ce genre de colonies de fourmis, ici sur un tore :
ADN
Des généticiens ont trouvé un morceau de l’ADN d’une fourmi de Langton, extrait avec l’aide du logiciel biopython :
from Bio import *
from Bio.Seq import *
gene = Seq("GAGGAGA"*7)
print geneEn fait ce génome n’est qu’une moitié de l’ADN :
GAGGAGAGAGGAGAGAGGAGAGAGGAGAGAGGAGAGAGGAGAGAGGAGA
Pour obtenir l’autre moitié il y a deux formes de réécriture :
- les lettres ont été changées (A et T échangés, C et G échangés) ;
- l’ordre des lettres a été inversé
On peut les obtenir avec ce code :
from Bio import *
from Bio.Seq import *
gene = Seq("GAGGAGA"*7)
print gene.complement()
print gene.reverse_complement()Voici à l’envers puis à l’endroit, l’autre moitié de la molécule d’ADN :
CTCCTCTCTCCTCTCTCCTCTCTCCTCTCTCCTCTCTCCTCTCTCCTCT
TCTCCTCTCTCCTCTCTCCTCTCTCCTCTCTCCTCTCTCCTCTCTCCTCEn rajoutant des barres indiquant des liaisons chimiques représentent la longueur du gène en notation unaire, on obtient un dessin de la molécule d’ADN complète :
GAGGAGAGAGGAGAGAGGAGAGAGGAGAGAGGAGAGAGGAGAGAGGAGA
|||||||||||||||||||||||||||||||||||||||||||||||||
TCTCCTCTCTCCTCTCTCCTCTCTCCTCTCTCCTCTCTCCTCTCTCCTCLa transcription génétique quant à elle est une réécriture des codons (sous-mots de 3 lettres comme « GAG »). Elle se fait en deux étapes :
Obtention d’un ARN messager
On transforme les « T » en « U » (comme uracile) dans la copie de l’ADN :
from Bio import *
from Bio.Seq import *
gene = Seq("GAGGAGA"*7)
ARN = gene.reverse_complement().transcribe()
print ARNCe qui donne cet ARN :
UCUCCUCUCUCCUCUCUCCUCUCUCCUCUCUCCUCUCUCCUCUCUCCUCEncore une histoire de UC, à moins que ça soit le reverse ?
De l’ARN à la protéine
Pour obtenir la formule chimique de la protéine synthétisée, on traduit chaque codon (sous-mot de longueur 3) en acide aminé. Par exemple le premier codon UCU correspond à une molécule de sérine notée S.
La protéine synthétisée par ce gène de fourmi de Langton a la formule suivante :
SPLSSLLSPLSSLLSP
Ainsi, la vie est peut-être juste un système de réécriture, ce qui peut expliquer qu’on simule des systèmes de tague de Post avec des ordinateurs à ADN, et l’approche d’Aristid Lindenmayer pour modéliser des plantes. Le sujet zéro de l’option « informatique » du CAPES de maths évoque les mutations génétiques par modification aléatoire de lettres dans le mot génétique.
Si les systèmes de tague sont (un peu) connus aujourd’hui, c’est parce que Marvin Minsky s’en est servi pour construire sa machine de Turing universelle. Il a ensuite travaillé avec un spécialiste de la notion de langage sans étoile : Seymour Papert ; ensemble ils ont créé un nouveau langage de programmation, fortement inspiré par Lisp : Logo (langage). Et comme ce langage a été créé pour les enfants, et bien que depuis on ait fait mieux, il peut être intéressant (et au moins autoréférentiel) d’utiliser Logo pour des activités sur le langage. Ce qui est proposé ici dans le bloc d’onglets suivant, destiné aux Logo-motivés.
Logiciel
Pour programmer en Logo, il faut un interpréteur Logo : C’est un logiciel qui écoute le clavier et permet à l’utilisateur d’entrer des instructions dans le langage Logo, et bien entendu d’exécuter ces instructions. Et ce logiciel, il fallait bien le choisir parmi l’immensité de l’offre présente. C’est, par proximité avec le Logo classique et parce qu’il est libre, le logiciel Xlogo qui a été choisi ici.

Ce choix est contestable, surtout dans une revue où GéoTortue a déjà été amplement utilisé. C’est que justement, lorsqu’il s’agit d’activités linguistiques, GeoTortue s’éloigne du Logo. C’est d’ailleurs ce qui est précisé dans la présentation : « Le langage de GéoTortue est un LOGO simplifié, où ne sont repris que les éléments de programmation qui servent directement la géométrie de tortue. »
Comme on va le voir dans les onglets suivants, Xlogo est, a contrario, un Logo complet, et pas uniquement axé sur des activités graphiques.
La page de téléchargement du logiciel est ici ; celle du manuel ici. En téléchargeant le logiclel, on se retrouve avec un fichier « jar », sur lequel il suffit normalement de double-cliquer pour lancer le logiciel Xlogo.
Dialogue
Lorsqu’on commence à programmer, quel que soit le langage de programmation, on essaye d’apprendre la politesse au logiciel de programmation, en affichant un message de bienvenue. Essayons :
![]()
Ça marche, mais le second guillemet est affiché à la fin du mot, ce qui veut dire qu’il fait partie du mot :
En Logo, un mot est délimité par un guillemet à gauche et une espace à droite
Comment alors écrire une phrase formée de plusieurs mots séparés par des espaces ?

En écrivant des mots après le premier guillemet, qu’ils soient suivis ou non d’un second guillemet, seul le premier mot est considéré comme un mot et les autres sont a priori des instructions ; du coup, il y a un message d’erreur disant que le second mot n’est pas une instruction connue de Logo. La coloration syntaxique montre d’ailleurs que seul le premier mot est colorié en bleu, et donc identifié comme un mot.
Une solution est montrée en bas de la copie d’écran ci-dessus : Faire une liste de mots, mais du coup les guillemets sont affichés avec, pour rappeler que ce sont des mots qui sont dans la liste.
Une meilleure solution est montrée ici, avec une phrase qui est une liste de mots :
![]()
Pour rendre Logo encore plus convivial, on peut insérer une entrée, permettant à Logo de connaître le nom de son interlocuteur, et de s’adresser nommément à lui :

Là encore, plein de leçons à tirer de cet exemple :
lis a pour effet de créer une boîte de dialogue modale où une entrée est sollicitée (ici le nom de l’interlocuteur) :

Mais aussi, il y a une affectation : Le second mot de l’instruction lis [Bonjour, quel est ton nom ?] « réponse est le nom d’une variable et donne lieu à un phénomène très important dans le monde de Logo, et sur lequel on reviendra souvent : L’enrichissement du vocabulaire. En effet, avant ça, Logo ne connaissait pas le mot »réponse" et aurait donné un message d’erreur du style je ne sais pas faire réponse si on y avait fait allusion. Maintenant, la variable réponse existe et sa valeur actuelle est le nom de Paul Bismuth (célèbre pseudo pour ceux qui veulent garder l’anonymat). En Logo comme dans les autres langages de programmation, il faut éviter de confondre le nom de la variable, avec la valeur de la variable. Pour désigner cette dernière, on remplace le guillemet par un double-point.
Ce qui permet comme on le voit ci-dessus, de constituer une phrase à partir de sous-phrases dont la seconde est le nom de l’interlocuteur.
Aire
On souhaite calculer l’aire d’un disque de rayon 5 cm, avec les fonctions de calculatrice de Logo. On essaye déjà de voir si la fonction carré existe (on ne rigole pas, beaucoup de lycéens préfèrent pianoter plutôt que lire le mode d’emploi avec la liste des mots du langage, et ensuite ils se plaignent parce que la fonction « carré » n’existe pas dans ce langage : C’est l’effet ELIZA, analysé plus loin) :

On constate par contre que le mot « pi » est connu de Logo, il a une signification qui devrait correspondre à celle de l’élève. Mais le mot « carré » n’existe pas encore dans le vocabulaire de Logo. Il le dit « je ne sais pas comment faire ». Pas encore ! On va donc le lui apprendre. Mais d’abord, il y a deux façons pour Logo d’ignorer le sens d’un mot : Ou bien c’est une fonction comme « carré » et Logo dit ne pas savoir quoi faire avec, ou bien c’est une variable qui n’a pas encore de valeur, et Logo sait distinguer les deux cas :

Ainsi, à ce stade, Logo sait que le rayon est 5, mais ne sait pas encore comment calculer son carré. Pour cela on définit la fonction carré [13] en entrant pour carré :n, ce qui, en plus, révèle que le carré est celui d’un nombre n. Dans Xlogo, cela a pour effet d’ouvrir une fenêtre d’édition dans laquelle on peut écrire un « script » Logo :

Une fois le script entré, on clique en haut à gauche ce qui a pour effet d’écrire dans la console un message disant que maintenant la fonction « carré » existe et que désormais (du moins dans la séance en cours) Logo connaît la signification de ce mot :

Et c’est ce que voulait Papert : Que le sujet apprenant puisse enrichir le vocabulaire de son micromonde, avec ses propres définitions ; et surtout que ces définitions puissent servir à définir d’autres mots en cascade :

On peut alors calculer des aires de disques à l’aide du nouveau mot, qu’il n’est d’ailleurs pas nécessaire d’écrire avec les majuscules là où on en a mis :

Mais Logo permet aussi de faire des choses plus linguistiques et pas seulement algébriques. On va en effleurer certaines dans les onglets suivants.
Tags
Avec Xlogo, le problème de 3-tag de Post se programme comme ceci :

Comme c’est un 3-tag, on doit répéter 3 fois l’instruction saufpremier qui n’enlève que la première lettre. Mais le système est binaire (à deux lettres « a » et « b ») et le suffixe est entièrement déterminé par un test sur la lettre « a » : Si la lettre n’est pas « a », elle est forcément « b ». Pour d’autres systèmes de tag, il faut des tests imbriqués qui compliquent le script.
Le système initial de Post donne ceci qui permet d’explorer la situation :

Palindromes
Un palindrome est un mot qui reste le même si on l’écrit à l’envers. Pour définir le mot « palindrome » dans Logo, on a donc besoin préalablement de définir le mot « envers » qui écrit le mot à l’envers. L’algorithme est le suivant :
- on crée un mot sortie initialement vide ;
- on parcourt les lettres du mot d’entrée (compte fournit le nombre de lettres de ce mot, donc le nombre de répétitions, le numéro de la lettre s’appelle compteur) ;
- dans cette boucle on ajoute cette lettre au début du mot sortie
Cela a pour effet de réécrire le mot, lettre par lettre, mais vers la gauche : Le mot se retrouvera bien écrit à l’envers après tout ça.
Le script :

Et son utilisation :
![]()
La suite devient très brève : La fonction palindrome dit si le mot auquel elle s’applique est égal au même, écrit à l’envers :

Ce nouveau mot fonctionne comme on le souhaite :

Effectivement si on écrit « baba » à l’envers on a « abab » qui n’est pas le même mot, alors que si on écrit « abba » à l’envers on a « abba » à nouveau : abba est un palindrome...
Cesar
Pour écrire un code de Cesar, on va faire un peu d’arithmétique modulo 57. Pourquoi 57 ? Parce que l’unicode le plus petit qui soit intéressant est celui de « A », soit 65, et l’unicode le plus grand est celui de « z » soit 122. Et combien font 122-65 ? Mmmm ?
On considère donc qu’on travaille dans un alphabet de 57 lettres (26 majuscules, 26 minuscules et quelques signes de ponctuation) et
- pour coder, on ajoute 13 (par exemple) à l’unicode de la lettre à coder ;
- pour décoder, on ajoute 57-13=44 à l’unicode de la lettre à décoder.
Dans les deux cas, on risque de dépasser 57 et on remplace donc l’unicode par le reste de sa division par 57 : « modulo ». En fait c’est un mot disant « le nombre lui-même s’il est assez petit, sinon on soustrait 57 pour le rapetisser ».
Et comme on travaille sur des nombres entre 65 et 122 (et non entre 0 et 57), on introduit un décalage de 65 vers le bas avant le codage ou le décodage, et vers le haut après : En théorie des groupes, on appelle cela une conjugaison. Enfin, on raccourcit un peu : Soustraire 65 et ensuite ajouter 13, c’est comme soustraire 65-13=52 d’un coup au début du codage. De même, pour le décodage, soustraire 65 et ajouter 44, c’est soustraire 65-44=21, ce qui raccourcit un peu les scripts de codage et décodage :

On a là un projet plus ambitieux que les systèmes de Markov et de Post. De quoi occuper une équipe de cryptographes collégiens pendant quelques mois, d’autant qu’il y a des recherches documentaires à faire sur unicode. Mais une fois fait, le résultat est plutôt probant (les caractères « espace » doivent être « échappés » par un « backslash » pour dire à Logo qu’ils font partie de la chaîne de caractères) :

Pour d’autres idées similaires, voir cet article sur le même sujet (mais en JavaScript)
Eliza
Un exercice à succès concernant la programmation Logo a été (en anglais) la programmation par des enfants, du logiciel Eliza (initialement programmé en Lisp).
Ce logiciel transforme les affirmations du « patient » en questions, pour entretenir un dialogue le plus longtemps possible. La complexité du programme étant sans limite si on veut se rapprocher arbitrairement de la langue naturelle, on peut envisager ce programme comme un projet [14]. Avec quelques bonnes surprises comme celle que fournit cette version Python :
Vous : Je voudrais savoir quelle est la puissance de calcul des langages sans étoile de Kleene.
Elizia : La langue ment à la parole et la parole à la pensée.
Ce genre de « chat bot » destinés, aujourd’hui, à réussir le test de Turing, est un bon exercice de grammaire pour des collégiens : Au lieu d’apprendre par cœur des règles de grammaire pour les appliquer ensuite, ils enseignent les règles à Logo, et développent ainsi une connaissance plus procédurale que déclarative, de la grammaire [15]. En ce qui concerne le test de Turing, il ne réussit pas toujours et ses échecs sont amusants. En fait, la faiblesse de ce genre de logiciel de conversation automatique est qu’ils ne font que de la syntaxe (par réécriture) et pas de la sémantique : Celle-ci nécessite de passer par la logique du premier ordre et même, depuis Richard Montague, par le lambda-calcul, évoqué dans la partie sur les oiseaux.
Toto
Toto le Robot en Logo sans Lego
Bien entendu, programmer Toto le robot est assez facile aussi en Logo, puisque comme Python, Logo a une tortue :

Après ça il suffit, pour faire des dessins, d’écrire quelque chose comme
faire "GADADAGADA
Historiquement, le permier système de réécriture qui ait été utilisé explicitement pour faire des calculs est la logique combinatoire de Schönfield et Curry. En voici une présentation ornithologique :
Fonctions
On peut réécrire les mots du style « GAD » sous forme de fonctions composées : Disons qu’on veut appliquer le mot « GAD » à une tortue « T » :
- On applique l’instruction « G » à la tortue « T », le résultat de cette application étant noté « G(T) » (et l’effet de bord est de faire tourner la tortue) ;
- on applique ensuite l’instruction « A » à la tortue tournée : Le résultat est alors noté « A(G(T)) » ;
- enfin on applique l’instruction « D » à la tortue tournée et avancée : Le résultat de l’application de « GAD » à « T » est noté « D(A(G(T))) ».
On obtient alors un système de réécriture pour transformer un mot de Toto le robot, en fonction (elle-même composée de fonctions) :
- inverser l’ordre des lettres (transforme « GAD » en « DAG ») ;
- compter les lettres (ici il y en a 3) ;
- insérer une parenthèse ouvrante entre deux lettres consécutives (on a alors « D(A(G »)
- ajouter un « (T » à la fin (on a maintenant « D(A(G(T »)
- rajouter en suffixe, un nombre de parenthèses fermantes égal au nombre initial de lettres, ce qui ici donne « D(A(G(T))) ».
Howard
En logique combinatoire, les parenthèses implicites sont au début et non à la fin, comme dans l’onglet précédent. Ce qui introduit un changement de paradigme :
L’écriture « G(T) » désigne l’effet du programme « G » sur la tortue « T », et suppose que G est une fonction qui, appliquée à une tortue, donne une tortue (la même mais tournée). Du coup l’écriture « A(G(T)) » est du même type que « A(T) » (fonction de l’ensemble des tortues dans lui-même) ; et les fonctions D, G et A sont composées. L’ancien paradigme, sur lequel ces élucubrations sont basées, est celui où on assimile un programme à une fonction, le programme agissant sur des objets d’un certain type, en retournant des objets du même type :
- un programme de calcul agit sur des nombres, et produit des nombres (c’est le paradigme de Sofus par exemple) ;
- un programme de construction agit sur une figure, et enrichit (à moins d’utiliser la gomme) cette figure, pour avoir une nouvelle figure (c’est le paradigme des CaRScripts par exemple) ;
- Mais Haskell Curry et William Alvin Howard se sont intéressés à quelque chose qui est en filigrane depuis le début de cet article : Des programmes agissant sur des programmes, et produisant des programmes (exemples : Correcteurs syntaxiques, compilateurs...)
Dans ces onglets, on appellera « programme » un « programme de programmes », qui agit sur des programmes. Ou qu’on « applique » à des programmes. C’est la correspondance de Curry-Howard, qui permet de ramener des démonstrations en logique, à des vérifications de type ; mais aussi, de ramener le lambda-calcul à un système de réécriture similaire à ce qu’on a vu ci-dessus.
Dans les onglets suivants, on va étudier certains programmes de programmes particuliers, que Raymond Smullyan compare à des oiseaux dans son livre « to mock a mockinbird », qui sera commenté dans la même optique.
SKI
La logique combinatoire a été créé par Moses Schönfinkel dans les années 1920, ce qui fait de lui et Haskell Curry (qui l’a très vite suivi), des précurseurs du lambda-calcul auquel la logique combinatoire s’applique. La logique combinatoire est la logique des combinateurs, et un combinateur est le nom donné aux « programmes de programmes » décrits dans l’onglet précédent.
Dans la théorie de Schönfinkel et Curry, tout programme de programmes peut être construit à l’aide de trois programmes (de programmes) particuliers, appelés ci-après I (« idiot bird »), K (« kestrel » soit crécerelle) et S (« starling » soit sansonnet). On en présentera d’autres, importants, ici :
- I est le programme qui ne touche pas à un programme : Tout programme transforme des programmes, mais pas I, qui les laisse invariants ; autrement dit, si on tente de modifier un programme x par l’application de I, on se retrouve avec x intact. On note ça I x = x, soit même sans espace Ix=x. Comme le programme x peut être choisi quelconque, ce comportement « idiot » se retrouve même avec des programmes spéciaux comme K : On a donc IK=K. Remplacer IK par K dans une expression de la logique combinatoire, c’est non seulement une réécriture, mais aussi ... du lambda-calcul ! Et qui a dit que c’était difficile le lambda-calcul [17] ?
- K (le « kestrel » chez Smullyan) est un programme qui s’applique à deux programmes x et y, et renvoie le premier. On peut donc considérer ce programme comme partiellement sourd, ou ne tenant pas compte de y. Mais sans la curryfication, c’est la projection sur l’axe des abscisses [18] : Du point (x,y) on ne garde que l’abscisse x...
- La symétrie par rapport à la première bissectrice est aussi une fonction de deux variables x et y : Elle échange x et y. Son équivalent combinatoire est le programme T (« thrush », soit « grive » chez Smullyan), qui, appliqué à deux programmes x et y, donne l’application de y à x : Txy=yx.
- le moqueur qui a donné son titre au livre de Smullyan, est un programme du type « drôle d’oiseau » : Appliqué à un programme p, il donne le résultat de p appliqué à lui-même : Mp=pp. Bien oui : Si on peut appliquer un programme à un programme, on peut en particulier appliquer un programme à lui-même (« compiler un compilateur » par exemple). Cette application est elle-même effectuée par un programme qui est M. Le titre du livre de Smullyan suggère d’appliquer M à M ; c’est très amusant d’essayer...
- Enfin le troisième des combinateurs de Schönfield, noté S (comme « substitution » mais aussi comme « starling » (étourneau) s’applique à trois programmes x, y et z : Il applique chacun des deux premiers au troisième, obtenant respectivement p=xz et q=yz, puis applique p à q.
La théorie de Schönfield et Curry se résume à ceci : Tout combinateur (ou « programme de programmes ») peut s’écrire comme une suite de lettres choisies parmi « I », « K » et « S », et le cas échéant de parenthèses.
Des exemples seront donnés dans les onglets suivants.
Voici déjà le bottin des oiseaux de Smullyan :
Moqueurs
Le livre de Smullyan propose de se moquer du moqueur, et déjà de voir ce qu’est un moqueur (le programme M) et les autres combinateurs (les principaux sont décrits dans l’onglet précédent). On complètera utilement sa lecture par celle de cet article illustré : Les dessins représentent les réseaux neuronaux des cerveaux des différents oiseaux, avec des réductions d’écritures montrées dans des films ; ce logiciel permet de tester les idées décrites dans le livre. Il y a aussi ce logiciel en ligne.
Le livre de Smullyan comprend ce surprenant hommage à Eva Joly :

Mais il y est surtout question d’oiseaux chantant des noms d’oiseaux dans des forêts plus ou moins mystérieuses ; par exemple il y est dit que « schön finkel » veut dire « bel oiseau » ou que Curry (que Smullyan semblait bien connaître) était féru d’ornithologie.
Oiseaux
Cette partie présente la logique combinatoire avec le vocabulaire des oiseaux chanteurs, et présente, outre les combinateurs S, K, I vus dans l’onglet qui leur est consacré, d’autres combinateurs comme
- Le programme L (« lark » soit alouette) est défini par Lxy=x(yy) : Appliqué à deux programmes x et y, il applique le second à lui-même, puis le premier au résultat.
- Le « sage bird » (Tetras) de Smullyan est noté Θ ; il a pour effet, appliqué à un programme p, de donner un programme qui reste invariant lorsqu’on lui applique p.
- Le programme B (« bluebird » soit bleumerle) s’applique à trois programmes x, y et z : Il applique le second au troisième puis le premier au résultat.
- Le programme W (« warbler » soit fauvette) s’applique à deux programmes p et q : Il applique p à q, puis le résultat encore une fois à q ;
- le programme C (« cardinal ») s’applique à trois programmes x, y et z : Il applique le premier au troisième et le résultat au second et implémente ainsi un échange des deux dernières variables.
- La chouette (« owl ») est aussi un programme appliqué à deux programmes p et q ; il applique le premier au second, puis le second au résultat ;
- Le programme de Turing noté U s’applique aussi à deux programmes p et q : Il applique p à lui-même, puis le résultat à q, et enfin, il applique q au résultat obtenu. Encore un drôle d’oiseau...
- Le programme R (« robin » soit « rouge-gorge ») est plus complexe puisqu’il s’applique à trois programmes x, y et z : Il applique le second au troisième, puis le résultat au premier. En fait il effectue une permutation circulaire sur x, y et z ( noter qu’en anglais « tourniquet » se dit « round-robin » )
Voici cette partie :
On a vu précédemment que S, K et I permettent à eux seuls de faire tout le lambda-calcul. La thèse de Curry dit que B,C,K et W aussi. D’autres bases possibles sont
- B,C W et I (Curry)
- B, T, M et I (Church)
- B, C, S et I
Cette partie se conclut par un résultat intéressant sur le programme U de Turing : UU est un « sage bird » c’est-à-dire qu’il a un point fixe.
Forêts
Les forêts qui sont décrites dans cette courte partie présentent des paradoxes logiques avec une concision permise par le lambda-calcul. Elles sont basées sur une ressemblance entre le système de réécriture de la logique combinatoire, et l’implication :
- à I (avec Ix=x) correspond l’axiome p ⇒ p de la logique propositionnelle ;
- à K correspond l’axiome p ⇒ (q⇒p) ;
- à S correspond [a⇒(b⇒c)] ⇒
a⇒b)⇒(a⇒c
- à L correspond (p⇒q) ⇒ [p⇒(q⇒q)]
La notation de la logique combinatoire permet donc une concision qui, à son tour, permet de poser des paradoxes classiques en terme de réécriture :
- Dans la forêt de Curry, on se concentre sur le combinateur Y = S(K(SII))(S(S(KS)K)(K(SII)))] qui a toutes les apparences de l’implication, mais qui mène au paradoxe de Curry si on essaye de l’interpréter comme l’implication.
- Dans la forêt de Russel, un combinateur similaire permet d’interpréter le paradoxe de Russell en logique combinatoire ;
- Dans la forêt sans nom, on étudie une variante du paradoxe de Curry ;
- Dans la forêt de Gödel, on introduit le théorème d’incomplétude de Gödel par la logique combinatoire.
Voici le récit de voyage de l’inspecteur Craig dans ces forêts :
Forêt du Maître
Renseignements pris auprès des inspecteurs Langton et Craig, le maître dont la forêt est décrite ici, ne serait pas Perlin dont la forêt avait été explorée dans la partie sur les L-systèmes.
Un gardien surveille l’entrée de la forêt du maître : Ne sont en effet, autorisés à pénétrer cette forêt, que ceux qui veulent y entrer !
Dans cette dernière forêt, on évoque les travaux de John Barkley Rosser sur la logique combinatoire :
En fait SKK=I puisque SKKp=Kp(Kp)=p=Ip pour tout programme p ; on peut donc calculer tout ce qui est calculable, uniquement avec les deux combinateurs S et K. Mais l’avantage d’un vocabulaire riche est qu’on a des expressions moins longues, donc plus faciles à comprendre.
On peut aussi faire tout le lambda-calcul avec seulement les combinateurs I et J, ce dernier étant défini par Jxyzw=xy(xwz) .
On s’intéresse aussi, avec Rosser, au sous-ensemble du lambda-calcul engendré par les combinateurs B, T et I.
Voici le roman de la forêt du maître :
Calculs
Dans cette partie, Smullyan montre comment on peut effectuer des calculs avec la logique combinatoire. Cela commence par la représentation des nombres avec des combinateurs.
Logique propositionnelle
Si on choisit de représenter le « vrai » par le combinateur K et le « faux » par KI (choix de Barendregt), alors
- R(KI) réalise une conjonction, c’est-à-dire que R(KI)KK=K, R(KI)K(KI)=R(KI)(KI)K=R(KI)(KI)(KI)=KI ce qui donne une table de vérité de la conjonction.
- TK réalise de façon similaire une disjonction.
- RK réalise une implication. Donc (RK)p(KI) est la négation de p si p=K ou KI
Une autre manière de définir la négation est de passer par le combinateur V (vireo) défini par Vxyz=zxy (appliqué à 3 programmes x, y et z, il applique le troisième au premier puis le résultat au second) : V(KI)K donne la négation vue comme combinateur.
Ces calculs booléens sont basés sur le fait que « Si p alors q sinon r » se calcule simplement par pqr (on applique p à q et le résultat à r) si p, q et r sont choisis parmi K et KI. Et cette simplicité de l’opérateur ternaire est elle-même une conséquence du fait que les opérateurs et les propositions sont des combinateurs : Avec le lambda-calcul, on peut appliquer une proposition à une proposition, ce qui n’est pas possible dans les langages de la logique classique (Frege, Russel, Hilbert, etc). Pour en savoir plus à ce sujet lire cet article.
Arithmétique
Pour faire des calculs sur les entiers naturels, on utilise
- la fonction « successeur » (x+1) définie comme V(KI), et
- pour le plus petit entier (celui qui n’a pas de successeur et à partir duquel on peut construire tous les autres) zéro, le combinateur I. Ensuite
- on code 1 comme successeur de zéro : V(KI)I
- on code 2 comme sucesseur de 1 : V(KI)(V(KI)I)
- on code 3 comme successeur de 2 : V(KI)(V(KI)(V(KI)I)) etc.
Ce choix, différent de celui de Church, est de Barendregt.
Alors
- T(KI) réalise la fonction « prédécesseur » (l’inverse de la fonction « successeur ») qui permet de simuler la décrémentation d’un registre ;
- TK teste la nullité d’un entier : TKI=IK=K et TKn=KI si n est strictement positif (I représente 0) ;
- Ces « instructions » sont ceux d’une machine à registres illimités qui peut calculer une somme avec la définition donnée par Peano dans ses axiomes : n+0=n et n+s(m)=s(n+m) où s désigne la fonction « successeur » ;
- De même le produit peut être programmé par les axiomes n×0=0 et n×s(m)=n×m+n ;
- Les puissances peuvent être calculées avec n0=1 et ns(m)=nm×n
- Ceci permet de calculer des puissances de 10 et donc d’effectuer des concaténations de mots écrits avec des chiffres.
Smullyan (ou est-ce Griffin ?) utilise cela pour coder les combinateurs avec la numérotation de Gödel [19]. Comme à son accoutumée, Smullyan revoit le théorème d’incomplétude de Gödel et les questions de calculabilité.
Toute fonction arithmétique calculable peut donc être calculée par des réécritures sur des mots écrits avec les lettres K, S, I et des parenthèses. Ce que Smullyan décrit avec cette poésie toute sylvestre dont le livre est imprégné :

Ceci suggère une idée de projet à faire avec Snap ! consistant à programmer des oiseaux de Smullyan sous forme de lutins Snap : Quand on définit une fonction de Snap, même des lutins peuvent maintenant être des variables de cette fonction. Ceci devrait faciliter la mise au point de tels oiseaux. Et ainsi, simuler la forêt de Griffin...
La règle pour quitter la forêt du maître est la suivante : Ne sont autorisés à sortir, que ceux qui veulent sortir :
Binaire
Pour représenter des nombres entiers en binaire, on compose les fonctions
- O(n)=2n (représentant le bit 0) ;
- I(n)=2n+1 (représentant le bit 1) ;
C’est cette représentation des entiers par des composées de fonctions, qui est utilisée dans le logiciel Coq, pour axiomatiser les entiers positifs (théorie Zarith). Mais un autre langage basé sur la lambda-calcul, plus concis que Coq, va être utilisé ici : CoffeeScript. Les scripts suivants peuvent donc être testés en les copiant-collant vers ce compilateur en ligne (cliquer sur « try CoffeeScript »).
On prend l’exemple de 42 (nombre) qui s’écrit en binaire 101010, et on effectue les réécritures suivantes sur 101010 :
- on écrit les chiffres binaires à l’envers (voir le premier onglet « fonctions » pour voir pourquoi) ; on a alors 010101 ;
- on remplace les 0 par des « O » et les 1 par des « I » (lettres majuscules) ; on a alors OIOIOI ;
- on insère des espaces pour signaler que ce sont des fonctions à composer : On finit par O I O I O I
Le nombre 42 s’écrit donc ainsi en CoffeeScript version lambda-calcul :
O = (n) -> 2*n
I = (n) -> 2*n+1
answer = -> O I O I O I
alert answerCe script explique que answer est représenté par la fonction JavaScript suivante :
function () {
return O(I(O(I(O(I)))));
}Cependant, le dernier chiffre I (en réalité, le premier chiffre puisqu’on écrit à l’envers) est considéré comme une fonction à laquelle on applique une fonction similaire. Ce script, légèrement plus long, permet de la considérer aussi comme une fonction appliquée à un nombre (en l’occurence, 0) :
O = (n) -> 2*n
I = (n) -> 2*n+1
answer = (n) -> O I O I O I n
alert answerLa fonction est à peine plus compliquée, et maintenant on travaille sur des entiers :
function (n) {
return O(I(O(I(O(I(n))))));
}En appliquant la fonction answer à z=0, on a enfin la réponse à la grande question sur la vie, l’univers et le reste :
O = (n) -> 2*n
I = (n) -> 2*n+1
z = 0
answer = (n) -> O I O I O I n
alert answer zLes fractions positives peuvent aussi être représentées par des mots binaires grâce à l’arbre de Stern-Brocot : Toute fraction peut être obtenue en appliquant à 1, dans un ordre donné, les fonctions homographiques D=$x+1$ et $G=\frac{x}{x+1}$ ; ou bien comme un mot écrit avec les lettres « G » et « D ». Par exemple 1/2=« G » et 2/3=« GD ».
Par exemple, une bonne approximation du nombre d’Or peut s’obtenir avec la fraction « D G D G D G » comme on le voit avec ce script :
G = (x) -> x/(x+1)
D = (x) -> x+1
u = 1
alert D G D G D G uDe même, tout irrationnel est décrit de façon univoque par un mot infini sur l’alphabet « G,D ».


















