Introduction
L’importance de la pratique du calcul mental dans la construction du concept de nombre est actée par tous. Les programmes scolaires insistent sur une pratique régulière avec différentes approches. Des compétences solides en calcul mental sont un atout majeur à une poursuite d’études scientifiques. Pour être juste, ce n’est pas une condition nécessaire, des contre-exemples existent. Cependant, des difficultés marquées en calcul mental peuvent devenir un véritable handicap. Nos élèves de ce début du XXI ème siècle forment les premiers bataillons des générations « Image ». Donner plus de place au mental dans l’enseignement, c’est lui donner plus de sens car en lien avec le vécu de l’élève. C’est aussi repositionner l’écrit et lui donner sa véritable place, celle du prolongement de la pensée. Enfin, associé à l’oral, le calcul mental réfléchi suscite des échanges dans la classe. Il permet d’apprendre par l’écoute des autres. Il a une fonction sociale qui permet de trouver un meilleur équilibre entre l’individu et le collectif, un des problèmes majeurs pour l’enseignant dans la gestion du groupe.
Les enquêtes internationales, notamment PISA, ont mis en évidence les difficultés des élèves français dans la résolution de problèmes et dans la capacité à s’investir et à rentrer dans une démarche de recherche. Ce constat est, en partie, la conséquence visible et mesurable de faibles capacités en calcul mental. Plusieurs études récentes montrent très clairement une corrélation forte entre ces deux domaines. Une aisance en calcul mental se prolonge naturellement par un sens solide du nombre et des opérations et facilite le choix des celles-ci dans une résolution de problème. En clair, de bonnes aptitudes en calcul mental améliorent de façon significative les compétences en résolution de problèmes.
Que l’enjeu soit scolaire ou social, cela devient très vite une évidence : la gymnastique mentale numérique est un pilier essentiel dans la construction de la relation aux nombres. L’aisance en calcul mental est un atout, elle donne une assurance dans la fréquentation avec les nombres : le ressenti, l’interaction entre les nombres, les multiples décompositions d’un nombre, en fait la relation intime que chacun d’entre nous construit avec ces êtres numériques. Et ils sont partout ! A y regarder de près, peu de domaines mathématiques échappent aux nombres. Même les « grands théorèmes » de géométrie du collège, Pythagore et Thalès, sont numériques ! L’application que l’on fait du théorème de Pythagore dans nos classes, renvoie plus souvent à une vision calculatoire que géométrique. Un élève en délicatesse avec le concept de puissance est déjà en situation de fragilité avec la formule de Pythagore, et je ne parle pas du théorème de Thalès où le concept de proportionnalité dans le rapport des longueurs nécessite aussi une bonne gymnastique numérique.
Et le jeu ? Pour des millions de français qui jouent avec les lettres : mots croisés, mots fléchés, Scrabble etc… , combien d’adeptes des nombres croisés ? Et les sudokus me répondrez-vous ! Attention, dans une grille de sudokus, on ne joue pas avec les nombres mais juste avec leurs images donc les chiffres. C’est un bon début, mais il faudrait aller plus loin pour développer une véritable culture ludique du nombre. Le chantier est immense. Pourtant, jouer avec un concept, c’est prendre de la distance, du recul, c’est tout simplement mieux le maîtriser. Concernant le calcul, une pratique régulière du jeu améliore, dans un premier temps, l’intuition et le ressenti pour se prolonger ensuite en sens du nombre et des opérations.
Une pratique ludique du calcul à l’école a plusieurs objectifs : permettre à l’élève de construire une relation « amicale » avec les nombres, contribuer à la construction d’un véritable sens du nombre et des opérations avec des connaissances solides et susciter l’envie d’aller plus loin pour découvrir l’univers des mathématiques. Au-delà de l’aspect motivant, la place du jeu dans l’école sera solide et durable à condition que sa pratique soit régulière et surtout qu’elle s’inscrive dans une véritable progression pédagogique qui se prolonge par des progrès mesurables. Eviter l’unique heure de jeux juste avant les vacances qui ne fait que conforter l’image du jeu comme accessoire de second plan sans véritable statut pédagogique.
Le calcul mental direct : automatisé et réfléchi
Derrière l’appellation « calcul mental » se cache des pratiques différentes et surtout des types de calcul mental différents. Pour le grand public, le calcul mental est souvent associé à une image d’Epinal : l’élève en blouse grise sur une estrade, récitant ses tables de multiplication. Le maître, l’air sévère, à ses côtés avec une règle en bois à la main. On peut même parfois entrevoir en arrière-plan un bonnet d’âne accroché au mur !
Cette image, qui fleure bon la 3ème République, associe calcul mental à mémorisation et automatismes. Elle est évidemment réductrice et incomplète. Elle a surtout besoin d’être dépoussiérée car elle gomme toute la dimension sens et associe l’élève à un « automath ». Cette vision passéiste du calcul mental est certainement un frein à un enseignement renouvellé et diversifié, pourtant essentiel à la mise en place du sens du nombre et des opérations.
Le calcul mental automatisé. De quoi s’agit-il ?
Comme son nom l’indique, c’est la partie en mémoire, celle pour laquelle la réponse à un calcul est immédiate et ne demande pas de réflexion. Un peu à l’image de ce qui est stocké dans le disque dur d’un ordinateur. Cette sollicitation du cerveau est en apparence sans effort. Des études montrent une grande stabilité dans le temps. Les tables de multiplication bien apprises le sont en général pour la vie.
Cette partie automatisée n’existe pas à la naissance, elle se construit progressivement dans le temps. Les premiers contacts avec les nombres et les opérations ont certainement une importance capitale. Les premiers résultats découverts et répétés avec des manipulations d’objets vont prendre sens et petit à petit s’automatiser. Le 1 et 1 va devenir 2, puis le 1 et 1 et 1 va devenir 3…
Dans le domaine des premiers apprentissages, Brissiaud montre bien l’importance du comptage-dénombrement. Ce dernier est une clé dans la construction du sens du nombre avec une véritable mise en relation quantité-nombre. A distinguer du comptage-numérotage, pratique rituelle de comptage qui à la couleur et l’odeur du dénombrement mais qui est vide de sens du nombre. Comme le dit Brissiaud, à l’école maternelle, il vaut mieux enseigner les 10 premiers nombres que les 30 premiers numéros.
Cette partie automatisée va se développer et s’enrichir au fil du temps avec des allers-retours permanents entre calcul mental réfléchi et calcul mental automatisé.
Le calcul mental réfléchi. De quoi s’agit-il ?
Dès l’instant où la réflexion est nécessaire avec des choix de procédures ou de stratégies, il ne s’agit plus de calcul mental automatisé mais de réfléchi. La partie automatisée devient un outil au service de sa propre partie réfléchie. En pratique, le calcul mental réfléchi, par la diversité des méthodes, se rapproche de la résolution de problèmes. Une pratique régulière du calcul mental réfléchi entretient et enrichit progressivement la partie automatisée. On rentre alors dans une sorte de cercle vertueux car, en se développant, la partie automatisée libère de l’énergie, une capacité de réflexion plus grande, qui va permettre d’accroître la difficulté dans le domaine du calcul mental réfléchi.
Dans la vie courante, il est fréquent de se retrouver dans une situation d’évaluation d’un prix, d’une surface, d’un pourcentage… qui correspond au résultat d’une ou plusieurs opérations. Il s’agit d’une situation de calcul mental direct qui se définit par une ou des opérations données et un résultat attendu, éventuellement approché. Pour l’atteindre, chacun dispose de sa partie automatisée et de ses connaissances numériques et opératoires qui lui permettent de pratiquer du calcul mental réfléchi. Le tout forme une partition personnelle évolutive.
Il faut bien comprendre qu’une partie automatisée peu développée sera vite source de blocage pour acquérir des connaissances ou des mécanismes dans d’autres domaines mathématiques. Les exemples sont nombreux : simplifier une fraction, appliquer ou calculer un pourcentage, appliquer une proportionnalité type règle de trois... L’aisance calculatoire est fortement corrélée à une partie automatisée riche.
Ces deux types de calcul mental, automatisé et réfléchi, illustrent bien la dichotomie, classique en mathématiques, entre sens et technique. Les « modes » pédagogiques ont parfois poussées plus fort vers le sens ou vers la technique. Mais, de toute évidence, le sens a besoin de fondations techniques maîtrisées et à l’inverse, la technique ne peut s’enraciner durablement qu’avec du sens ! Sens et technique, particulièrement en calcul mental, sont imbriqués et se nourrissent l’un de l’autre. Ne les opposons pas, ils sont intimement liés !
Le discours actuel de l’institution insiste de façon forte sur la tâche complexe en donnant parfois l’impression d’en faire un cheval de bataille. Or, sans un travail technique en amont et en parallèle, notamment en calcul mental mais aussi à l’écrit, cela revient tout simplement à mettre la charrue avant les bœufs ! L’observation des dernières épreuves de mathématiques du brevet des collèges confirme cette analyse. Là, où le brevet proposait il y a 10 ans et plus, une succession de questions techniques sans aucune prise d’initiative, l’institution propose désormais des sujets avec une quasi absence de questions techniques. Pourquoi un tel déséquilibre ? Les critiques des anciens sujets étaient justifiées, celles d’aujourd’hui pour des raisons diamétralement opposées le sont aussi. La période des maths modernes avec ses excès n’est pas si lointaine, ce discours actuel déséquilibré interroge...
Le calcul mental direct ne se prête pas idéalement à une mécanique ludique. Les tentatives de création de jeux de société, avec des opérations en ligne qui s’entrecroisent sur un plateau sur le principe de Scrabble, n’ont jamais donné de résultats très probants. On peut vite avoir l’impression de se retrouver devant un exercice scolaire. Mathable, jeu canadien, est une des rares exceptions. Il y a aussi des jeux de cartes qui développent une mécanique ludique intéressante. Par exemple, Lobo77 combine défausse de ses cartes avec un système cumulatif (addition et soustraction) de points et un seuil 77 à ne pas dépasser. Le jeu est vivant et très plaisant. « 6 qui prend » rencontre également du succès.
Le calcul mental à l’envers : une clé
En quelques mots, le calcul mental à l’envers, c’est le concept universel du « Compte est bon » : un nombre-cible et des nombres sur lesquels on opère avec les quatre opérations de façon à fabriquer cette cible.
Cette gymnastique du calcul mental à l’envers est une clé pour la perception des ordres de grandeur et le sens du nombre et des opérations. En effet, la cible à fabriquer est inconsciemment analysée avant de chercher à l’atteindre. Cette analyse peut être succincte voire inconsciente mais aussi très riche. Elle incite à décomposer, à casser le nombre. Par exemple, pour fabriquer 63, je peux solliciter du calcul automatisé comme 7x9 ou 3x21, semi-automatisée comme 6x10+3 ou 7x10-7 ou des décompositions comme 5x12 + 3 ou 5x13 - 2 ou 7x8 + 7 ou 8x8 – 1 ou 5x14-7 etc… Ces choix sont fonction des nombres dont on dispose mais surtout de ses propres connaissances numériques et opératoires. Il est important de préciser qu’en calcul mental à l’envers comme en calcul mental direct, on retrouve la dichotomie automatisé et réfléchi : 25 déclenche un 5x5 mais 91 ne déclenchera pas toujours un 7x13. En complément d’une pratique classique du calcul mental direct, le calcul mental à l’envers est idéal pour donner du sens au calcul mental direct car ce dernier devient un outil pour fabriquer cette cible.
Avec cette gymnastique mentale, les aller-retours entre réfléchi-automatisé d’une part et direct-à l’envers d’autre part, sont permanents et créateurs de sens dans la relation aux nombres et aux opérations. Ils créent des liens entre sens et technique et donnent de l’épaisseur aux nombres. Cette pratique stabilise et enracine les connaissances en calcul mental direct. L’objectif d’atteindre ce nombre-cible rend acteur par les choix de nombres et d’opérations à effectuer. L’ « automath » ne peut plus fonctionner !
Ce mélange de tests et de tâtonnement raisonné constitue un vrai travail sur les ordres de grandeur, autre clé du sens du nombre. Dans le cadre scolaire, en parallèle des apprentissages classiques du calcul mental direct, cette pratique de recherche d’un nombre-cible est à mettre en place de façon méthodique et organisée dans la classe car c’est un principe non naturel. Les formes, ludiques ou non, peuvent être diverses et variées. La pratique habituelle en classe est plutôt portée vers le calcul direct : une opération, un résultat attendu. La mise en place du à l’envers bouleverse ce schéma. Cette nouvelle gymnastique change les repères. Pour certains élèves, la logique habituelle « une opération, un résultat » induit l’idée fausse du chemin unique pour obtenir ce résultat, schéma mental accentué par l’apprentissage des tables. La mise en lumière de différents chemins en calcul direct combinée avec la gymnastique de la pratique du calcul mental à l’envers est alors riche de sens et permet de dépasser cette vision du chemin unique. Autre atout fort dans la pratique du à l’envers : un ressort ludique quasi naturel lié à l’aspect défi, on veut trouver ce nombre-cible ! Cette fréquentation des nombres avec des allers-retours opératoires entre direct et à l’envers permet de cultiver plaisir et effort intellectuel. C’est aussi une façon de poser les fondations d’une relation amicale et apaisée avec les nombres. Le principe du calcul mental à l’envers se prête bien à un habillage ludique.
Trio et Mathador, exemples de deux jeux pour pratiquer le calcul mental à l’envers
Trio, un jeu de grille
Trio se compose de 49 jetons carrés avec des chiffes de 1 à 9. Il faut les disposer en sept lignes de sept jetons (voir photo ci-dessous). Un nombre-cible (entre 1 et 50) est tiré au hasard. Objectif : fabriquer ce nombre-cible avec trois nombres alignés et voisins dans la grille que l’on combine avec les quatre opérations. Les trois nombres choisis peuvent être alignés horizontalement, verticalement ou en diagonale. La règle de base exclut la division et impose une multiplication suivie d’une addition ou d’une soustraction. Mais on peut très bien jouer en laissant le choix total des opérations. On peut aussi imposer une opération. De nombreuses variantes sont possibles. Le premier qui trouve, marque un point et on totalise les points pour établir le gagnant. On peut aussi laisser un temps de jeu et tous ceux qui ont trouvé marque un point. C’est une règle conseillée pour la classe pour éviter de laisser la parole aux plus rapides.
Trio est un subtil mélange fait d’automatismes et de réflexion. La recherche du nombre-cible incite à tester, à tâtonner en utilisant ses connaissances en calcul mental direct et en tenant compte des ordres de grandeur. Le calcul pratiqué alterne automatisé et réfléchi. Le sens des opérations est omniprésent par les choix opératoires à effectuer que la mécanique de Trio impose. Ce jeu donne un véritable statut d’outils aux connaissances automatisées. Pratiqué régulièrement, il entretient et consolide les automatismes. Il améliore la fréquentation des nombres et enrichit la panoplie des décompositions. La notion de défi, très présente, apporte un piment supplémentaire au plaisir de jouer.
Il présente l’intérêt d’une mise en place rapide et peut se jouer quelques minutes avec toute une classe. La grille ou une photo peut être vidéoprojetée. Les fichiers Jeux 5 et 6 de l’APMEP permettent une construction du jeu.

Dans le cadre d’un fonctionnement de classe, il est intéressant d’annoncer au préalable le nombre-cible sans la grille et de demander aux élèves des exemples de fabrication de 41 avec trois nombres. Les réponses attendues sont nombreuses :
5x7+6 ; 5x8+1 ; 5x9-4 ; 6x6+5 ; 6x7-1 ; 6x8-7 ; 7x7-8.
Ces décompositions de 41 sont ensuite à rechercher dans la grille.
Pour annoncer une solution, il est pratique de demander à l’élève de préciser le chiffre et sa couleur de façon à rapidement identifier l’emplacement précis dans la grille où se situe le calcul. Ensuite, il peut annoncer son calcul. Par exemple, j’annonce le 5 jaune dans la 4ème colonne et horizontalement, j’effectue 5x8+1. Ou, le 6 bleu dans la 3ème colonne puis verticalement 6x8-7. Ou, le 6 jaune dans la 3ème colonne puis en diagonale 6x7-1.
Le professeur au tableau peut facilement montrer la ou les solutions annoncées à l’ensemble de la classe depuis son ordinateur en pointant les cases annoncées avec la souris ou directement sur l’écran avec une grande règle.
Possibilité de jouer en ligne à Trio.
Mathador, un jeu de dés
Mathador Flash est un jeu de calcul mental qui utilise sept dés multifaces. Un lancer des cinq dés blancs (les 5 solides de Platon) à 4 ; 6 ; 8 ; 12 et 20 faces donne cinq nombres. Ce sont les nombres avec lesquels les joueurs peuvent effectuer tous les calculs possibles de façon à fabriquer un nombre-cible. Ce dernier, entre 0 et 99, est déterminé par le lancer de deux dés rouges. Il y a deux formules de jeu. Dans la 1ère formule, la plus simple, le premier joueur qui trouve le nombre-cible marque un point. L’autre formule, appelée Expert, est plus pédagogique et particulièrement adaptée pour la classe. Il s’agit de fabriquer le nombre-cible mais en essayant d’obtenir le plus de points possibles sachant que chaque opération utilisée rapporte des points. L’addition rapporte un point de même que la multiplication. Ce sont les deux opérations à la base de notre système de numération. Le choix naturel d’opérations nous pousse vers ces deux opérations car elles sont plus simples. La soustraction et la division sont les deux opérations contraires. Mentalement, elles sont plus difficiles. Pour inciter le joueur à les pratiquer et donc à mieux les maîtriser, la soustraction rapporte deux points et la division trois points. Le coup Mathador consiste à fabriquer le nombre-cible en utilisant les cinq nombres et les quatre opérations chacune une fois. Il rapporte treize points. Chaque joueur totalise ses points au cours de la partie qui peut se composer de cinq lancers. Le gagnant est celui qui totalise le plus de points.
Comme Trio, Mathador Flash est un jeu dans le registre du calcul mental à l’envers. On retrouve dans la mécanique du jeu cette proximité entre calcul mental automatisé et réfléchi avec, dans la recherche du nombre-cible, des allers-retours entre calcul mental direct et à l’envers. Pratiqué régulièrement, il entretient et consolide les connaissances du joueur. Ce dernier est incité à tester en permanence et pratique donc une forme de démarche scientifique. La notion d’ordre de grandeur est toujours présente. Le système de points de la règle incite à complexifier son calcul et à utiliser les opérations contraires que sont la soustraction et la division de façon à obtenir le maximum de points. Cette pratique améliore la fréquentation des nombres tout en développant le sens des opérations. La notion de défi très présente apporte un piment supplémentaire au plaisir de jouer. Comme Trio, il présente l’intérêt d’une mise en place rapide. En classe, on peut faire lancer les dés par les élèves puis noter au tableau le tirage des sept nombres de façon à faire chercher toute la classe. Comme pour Trio, il est intéressant de trouver et de verbaliser des décompositions du nombre-cible avant de connaître les cinq nombres donnés par les dés blancs. Quelques minutes de recherche peuvent ensuite déboucher sur une analyse collective des différents chemins qui permettent de fabriquer le nombre-cible. Il est important de préciser qu’un support écrit est tout à fait possible. C’est l’occasion de bien distinguer les différentes opérations qui s’enchaînent. De façon à rester dans un cadre mental, il faut demander à l’élève d’écrire ses opérations en ligne mais de ne pas les poser. En effet, les techniques opératoires renvoient plus aux chiffres qui composent le nombre et peuvent éloigner du sens du nombre. Ensuite, il est très intéressant d’écrire au tableau les différentes solutions avec les totaux de points correspondants de façon à les hiérarchiser puis à institutionnaliser différentes procédures. Ce prolongement écrit, qui prend du temps, peut se faire de façon non systématique et notamment lorsque le tirage de dés s’y prête bien par la richesse et la diversité des différents chemins.

Une situation simple avec 28 à fabriquer avec : 4 ; 6 ; 8 ; 4 et 7
4x7 rapporte 1 point
4x6 + 4 rapporte 2 points
Deux solutions très simples accessibles aux élèves en difficulté.
L’élève plus à l’aise en calcul mental pourra ensuite rechercher des solutions avec plus de points comme :
4x8 – 4 (3 points)
(7 – 4)x8 + 4 (4 points)
(7x8) :(6 – 4) (6 points)
(4x6 + 4) :(8 – 7) (Coup Mathador 13 points)
(7x8) :(4 + 4 – 6) (Autre coup Mathador 13 points)

Autre exemple avec 38 à fabriquer avec 4 ; 1 ; 3 ; 10 et 5
4x10 – 3 + 1 (4 points)
4x10 – 5 + 3 (4 points)
3x10 + 5 + 4 – 1 (5 points)
5x10 – 3x4 (4 points)
5x(10 – 1) – 4 – 3 (7 points)
(5x10 – 3x4):1 (7 points)
(4x10 – 5 + 3):1 (Coup Mathador 13 points)
Dans l’idéal, les différentes solutions doivent être proposées par les élèves. C’est l’occasion d’échanger sur la pertinence de certains choix, de proposer des pistes qui pourront être réutilisées. L’enseignant pourra proposer d’autres solutions pour compléter. Par l’écoute des solutions, chacun peut enrichir ses connaissances et découvrir d’autres stratégies. Le passage par l’écrit permettra d’institutionnaliser certaines procédures.
L’intérêt d’une mise en action rapide permet à ces jeux d’être des variables d’ajustement de fin d’heure sachant qu’il est possible de jouer quelques minutes. Avec l’organisation horaire du collège, la mise en place de jeux n’est pas toujours facile. Paramètre important pour un réinvestissement des nouvelles connaissances et nouvelles stratégies, il faut installer ces pratiques ludiques et de calcul mental dans la régularité. C’est une condition indispensable pour permettre à chacun de construire sa relation aux nombres et aux opérations.
Canopé Besançon propose depuis 4 ans maintenant pour les classes de l’académie de Besançon du CE2 à la 3°, un concours annuel de calcul mental basé sur les règles de Mathador Flash avec le système des points par opération. Réparties dans quatre catégories selon leur niveau (cycle 3, 6°-5°, 4°-3° ou Segpa-Erea), les classes ont seize défis hebdomadaires répartis sur l’année scolaire entre novembre et avril avec une période d’entrainement en octobre. Les élèves disposent de trois minutes pour trouver une solution. Des dizaines ou des centaines de solutions sont possibles pour chaque défi avec pour chaque tirage, des solutions simples en quelques points ou des solutions complexes avec un coup Mathador pour chaque tirage. De cette façon, chaque élève, quelque soit son niveau en calcul mental, est susceptible d’atteindre ce nombre-cible et il dispose de plusieurs mois pour trouver des stratégies plus complexes. L’originalité du concours réside dans l’alchimie individu-collectif puisque chaque élève est acteur et propose sa solution et c’est la moyenne de la classe (somme de tous les points divisée par le nombre d’élèves) qui est retenue pour le classement final. Cette « note » de classe entre 0 et 13 est un indicateur de performance en calcul mental de la classe. C’est son évolution au cours de l’année qui est intéressante avec une double lecture par élève et globalement pour la classe. Ce principe de concours a été proposé au niveau national par Canopé Besançon pour la semaine des mathématiques 2015. Il sera très certainement prolongé en 2016. D’autre part, le concours annuel pour les classes devraient être étendu à la rentrée 2016 à l’ensemble de la France. A suivre…
Et le numérique ?
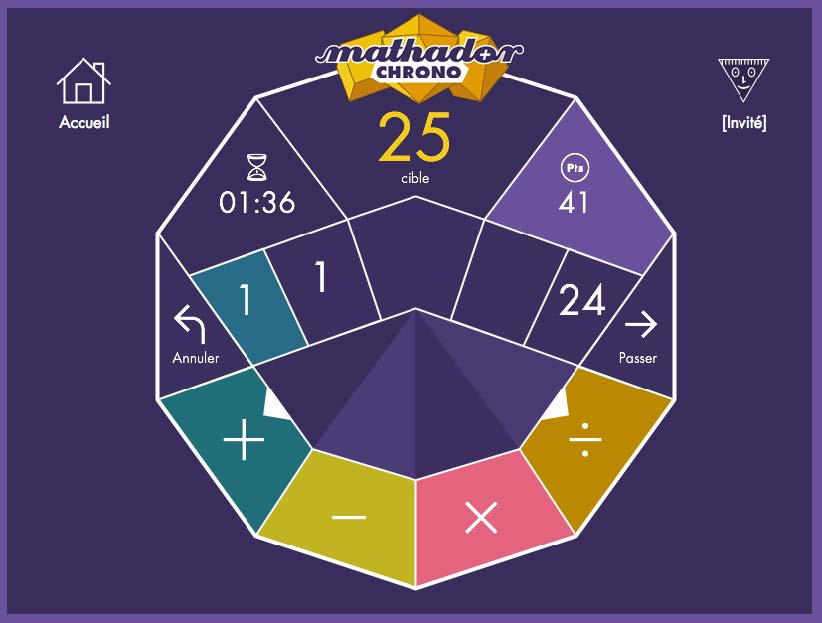
A l’image d’un travail de gammes en musique ou en sport, le jeu sur écran se prête bien à l’aspect répétitif du calcul mental direct. L’écran facilite le test et le tâtonnement. En effet, le caractère définitif et sacralisé de l’écrit s’efface derrière une démarche plus intuitive et plus instantanée que permettent l’écran et le clavier. Quelques sites sur le net sont de belles réussites et donnent la possibilité de pratiquer avec plaisir le calcul mental : Calculatice, développé par une équipe de l’académie de Lille, en est une parfaite illustration. Sur le site, toute une batterie de jeux en ligne, un rallye annuel pour les classes du CP à la 6ème, succès garanti dans les classes et à la maison aussi ! Evidemment, Mathenpoche dans ses parties de calcul mental combine bien travail sur les automatismes et dimension ludique. Mathador Flash peut aussi se pratiquer en ligne, une partie correspond à 10 lancers de dés. Les points se cumulent et donnent un indicateur calcul mental intéressant notamment avec son caractère évolutif sur la durée d’une année scolaire. Les sites « mathématiques magiques » et Matoumatheux sont d’autres exemples d’une alchimie réussie entre écran et calcul mental. Au même titre que l’ardoise, écran statique, l’écran de la tablette apporte de la dynamique à la pratique du calcul mental. C’est dans cet esprit qu’avec l’équipe de Canopé Besançon, nous avons prolongé les jeux Mathador dans l’univers du numérique. Les deux premières applications Mathador pour l’univers Apple sont sorties en 2014. Juin 2015 verra l’arrivée de Mathador Chrono qui présentera l’intérêt d’être disponible sur tous supports (ordinateur et tablette), de pouvoir faire des parties à plusieurs à distance et d’être gratuite. Son principe : accumuler le plus de points possibles sur le principe de Mathador Flash en un temps limite de 3 minutes avec autant de tirages que l’on veut. D’autres déclinaisons suivront à l’automne 2015 dont une spécifiquement pour la classe.

Où jouer ?
On peut jouer en classe avec la classe entière mais le jeu peut trouver sa place dans d’autres lieux de l’environnement scolaire de façon à construire des passerelles avec l’objectif de créer une véritable culture ludico-mathématique.
Lorsqu’il existe, le fonctionnement en petits groupes est idéal sachant que le jeu suscite envie et motivation. Une gestion en classe entière n’est pas toujours aisée. Avec la classe entière, la gestion en ateliers jeux est une possibilité supplémentaire sous réserve de disposer de l’espace nécessaire. L’aide personnalisée, l’accompagnement éducatif sont des moments privilégiés pour utiliser le support jeu et diversifier les approches.
Le professeur des écoles, qui vit avec sa classe, pourra si il dispose de la place nécessaire, créer un coin jeux dans sa classe. Cet espace, devenant un lieu clairement identifié jeu, est alors à la disposition permanente de l’enseignant et de sa classe et peut se gérer de façons diverses.
Le professeur du secondaire ne vit pas avec un groupe mais voit défiler des groupes, heure après heure. Ce fonctionnement en tranches horaires est un frein à la mise en place d’activités nécessitant du matériel comme le jeu. Les jeux de calcul mental, cités ci-dessus, ont l’avantage d’être utilisables sur de courtes séquences. Pour faire vivre d’autres jeux, le club jeux mathématiques est le fonctionnement idéal. Il suffit de disposer d’une armoire pour ranger les jeux et d’une salle disponible pour le club une ou deux fois par semaine. Le FSE de l’établissement peut aider financièrement le club de façon à équiper progressivement en jeux. C’est aussi l’occasion de pratiquer l’origami ou la préparation aux concours type Kangourou ou FFJM. Les pistes sont très nombreuses.
Ci-dessous, une liste non exhaustive de jeux qui ont leur place dans un club jeux logiques et mathématiques :
Nombres : Triolet, Mathable, Mathador, Multiplay, Shut the Box, Zatre, Algorix, Détective Mathéo, Lobo77, 6 Qui prend
Géométrie : Blokus, Katamino, Tangram
Logique : Mastermind, Puissance 4, Quarto, Abalone, Othello, Logix, Set
Les activités mentales et le jeu à l’école, un chantier encore en construction…
La place du mental et du jeu à l’école pose indirectement la question de l’équilibre avec l’écrit, particulièrement pour le calcul avec l’équilibre entre calcul écrit et calcul mental. Dans l’enseignement, la culture de la trace écrite est très forte. L’élève, qui demande dans une résolution de problème si il doit poser 28+9, en est l’illustration et la caricature.
Les techniques opératoires écrites utilisent du calcul mental mais sur des zones très localisées du nombre. Par exemple, si je pose 537+299, je commence avec les unités, puis je passe aux dizaines et aux centaines sans oublier les retenues. Ce travail technique demande attention et concentration et éloigne de la perception globale du sens de ces deux nombres 537 et 299. Alors qu’en calcul mental, j’ai intérêt à procéder différemment en intégrant la globalité de ces nombres en procédant, par exemple, par un ajout de 300 à 537 avant de soustraire 1. Le calcul mental nous met plus en relation avec la globalité du nombre alors que le calcul écrit et posé nous relie davantage avec les chiffres qui composent ce nombre. De ce fait, le mental, plus que l’écrit, nous rapproche du sens du nombre et permet certainement d’établir des liaisons plus fortes entre les différentes zones du cerveau qui traitent les nombres. Le sens se mentalise et l’écrit devrait toujours être le prolongement de la pensée, est-ce toujours le cas ?
Quant au jeu, sa place en tant qu’outil pédagogique à part entière, est encore en construction. Son installation se fait par capillarité, c’est la preuve par l’action. Le jeu est une porte d’entrée dans l’univers des mathématiques et une façon de lutter efficacement contre le développement de l’innumérisme. Il est certainement le meilleur antidote à l’effet anxiogène des mathématiques cité dans de nombreuses études.
Eric Trouillot, professeur au collège Victor-Hugo à Besançon