Note de l’auteur : Cet article fait suite à un atelier animé par Jean-Claude RENOULT et moi-même, lors des Journées Nationales de l’APMEP 2014 à Toulouse.
Note de l’auteur : Cet article fait suite à un atelier animé par Jean-Claude RENOULT et moi-même, lors des Journées Nationales de l’APMEP 2014 à Toulouse.
Cet article peut être librement diffusé et son contenu réutilisé pour une utilisation non commerciale (contacter l’auteur pour une utilisation commerciale) suivant la licence CC-by-nc-sa http://creativecommons.org/licenses/by-nc-sa/3.0/fr/legalcode.
NDLR :
Hervé Chastand est retraité, professeur de mathématiques au lycée Maine de Biran de Bergerac jusqu’à juin 2015. Il a assuré la responsabilité de la formation du Capes de Mathématiques de 2002 à 2004 et celle des PE/PLP de 2009 à 2011 à l’IUFM de Polynésie Française.
Pourquoi ce titre ?
JeuGebra est créé avec le logiciel GeoGebra.
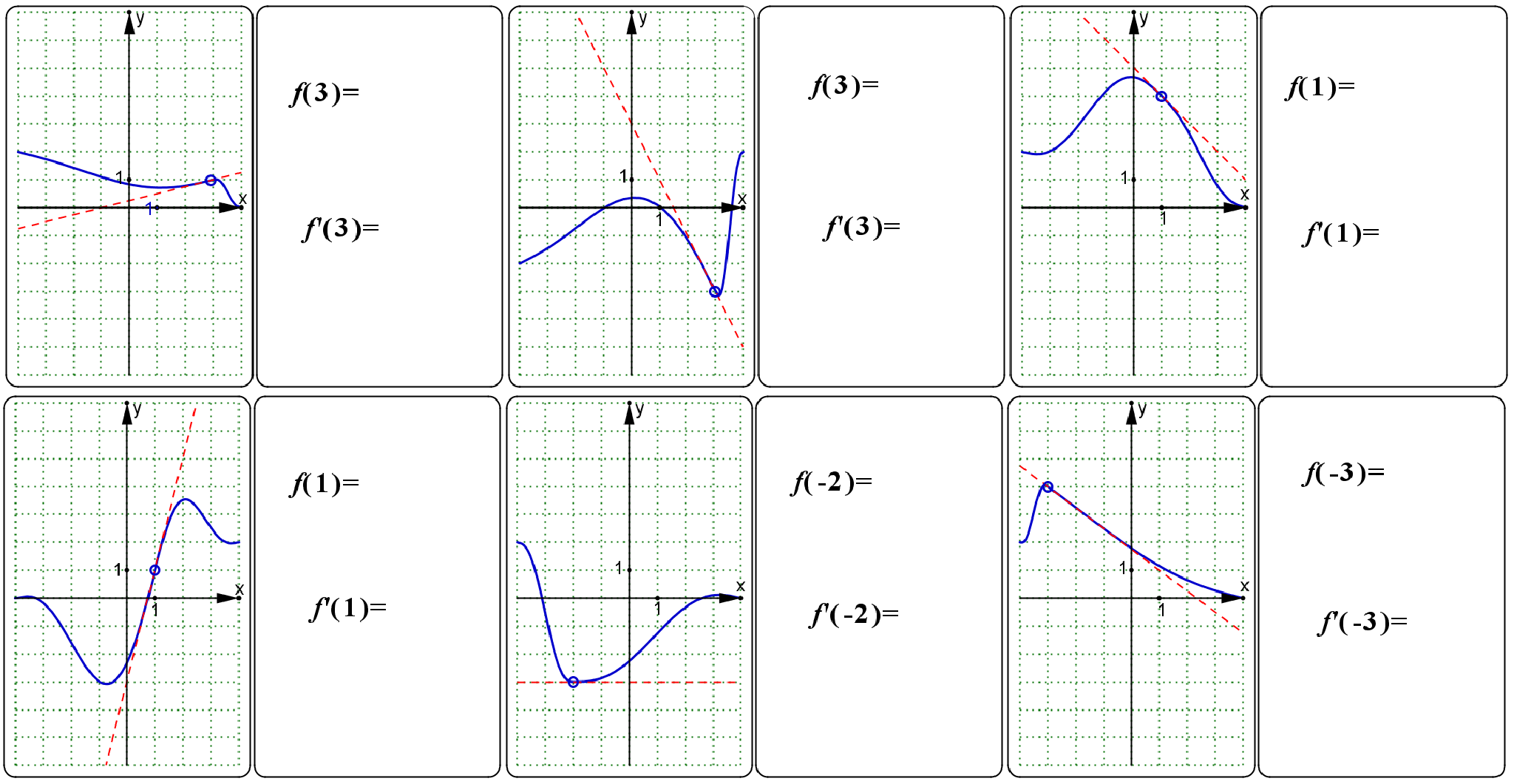
Il s’agit de jeux de dominos, de cartes, ainsi que d’une douzaine de casse-têtes (l’Âne Rouge) de type « taquin », s’adressant aux professeurs et élèves de premier et second degré.
L’idée de départ est de pouvoir utiliser un double support ludique, virtuel (informatique) et physique (papier ou carton), avec, la plupart du temps, création aléatoire des nombres utilisés, parfois paramétrables par curseurs.
L’ensemble des fichiers se présente sous forme de plus de 500 appliquettes GeoGebraWeb HTML5, stockées directement sur le site JeuGebra (non dépendantes du cloud GeoGebraTube de GeoGebra) : le format HTML5 permet d’exécuter ces appliquettes sur tout ordinateur, et aussi sur la plupart des tablettes et smartphones (contrairement aux appliquettes Java).
Exerciseur libre : licence Creative Commons non commerciale, avec modifications possibles (cc-by-nc-sa), ce qui signifie que tous les fichiers sont en libre accès, modifiables, imprimables et éditables sur d’autres sites, à condition de citer le nom de l’auteur, de ne pas en retirer un bénéfice commercial (publicité, etc.) et de diffuser les modifications suivant la même licence.
Il est possible d’utiliser JeuGebra en ligne ou en local (« Télécharger JeuGebra » sur la page d’accueil de l’application) : l’installation en local (30Mo) permet de s’affranchir des absences ou lenteurs de connexion, fréquentes dans certains établissements : tout enseignant utilisant régulièrement une salle informatique a vécu un jour l’angoisse (ou l’excitation !) d’improviser un plan B, faute de connexion Internet...
Chacune des deux catégories de fichiers (du type dominos ou cartes) est programmée avec un squelette analogue dans le tableur de GeoGebra : tout utilisateur de GeoGebra peut donc en théorie modifier ou créer des fichiers de type JeuGebra avec un peu de maîtrise du tableur de GeoGebra.
Apprentissages automatisés ou réfléchis : les exercices proposés (en général aléatoires sur un thème donné, correspondant à des savoir-faire identifiés nécessitant des automatismes et/ou de la compréhension) peuvent être répétés autant de fois qu’on le désire, par appui sur un bouton de réinitialisation.
OK, mais pourquoi créer un exerciseur pour les apprentissages automatisés ou réfléchis ?
Stanislas Dehaene, lors de sa remarquable conférence inaugurale du samedi 17 octobre au congrès 2014 de l’APMEP, a su expliciter certaines observations pédagogiques que ressentent beaucoup d’enseignants de mathématiques : il a, par exemple, développé l’idée que les apprentissages automatiques permettent de mettre en place des connaissances implicites, rapides et non-conscientes, libérant de la place pour les traitements explicites et conscients du cortex pré-frontal (là où on « réfléchit »). Lors d’une précédente conférence, il a illustré cela par une analogie avec la lecture en présentant le texte suivant :
Revenons en enfance...ll ni a peu tè tre pa de jour de notre an fan ce ke nou ai ion si plène man vé ku ke ce ke nou a voncru lè cé san lé vi vre, ceux quenous avons passés avec un livrepréféré.Marcel Proust, Sur la lecture
Constatation : on mobilise tellement notre cerveau pour déchiffrer la première partie que l’on n’en saisit pas le sens, alors que la dernière partie est limpide (les routines de lecture permettant de saisir immédiatement la signification de celle-ci).
Cela illustre bien la réflexion que fait souvent un professeur de mathématiques à propos d’un élève : « il a de bonnes idées, mais il ne peut pas les mettre en forme dans un algorithme structuré, car le moindre calcul lui demande un tel effort qu’il lui fait oublier l’essentiel : son raisonnement initial ».
Problème : il semble à beaucoup (?) d’entre nous que les apprentissages automatiques sont actuellement pour le moins dévalorisés dans l’enseignement des maths...
En effet, ils sont fastidieux (pour les professeurs comme pour les élèves), et les résultats obtenus actuellement paraissent peu efficaces avec les méthodes traditionnelles, du fait (entre autre), que les élèves veulent des résultats immédiats (problème de la relation au temps, qui « s’accélère »), avec récompense (ça doit être juste). Les élèves ayant des difficultés, on préconise de faire le moins possible de calculs répétitifs, les calculatrices servant de boîte noire « magique » : position démagogique qui n’aide pas l’élève à se structurer ! S’il est vrai que passer des heures à faire des exercices répétitifs ne constitue pas l’essence de l’apprentissage des mathématiques, ne plus en faire n’est pas une solution non plus...