Cet article résume un travail réalisé dans le cadre du laboratoire de mathématiques du Lycée de Vizille (38). Racine de deux est utilisé comme fil conducteur pour une dizaine d’exercices, posés dans différentes classes du lycée à la suite d’une réflexion sur l’utilisation de l’histoire dans l’enseignement des mathématiques. On aborde successivement les algorithmes d’approximation, l’irrationalité, les constructions géométriques et l’optimisation. Les thèmes vont de la géométrie à l’analyse, en passant par l’arithmétique et l’algèbre. L’environnement historique des notions abordées est développé dans le site Histoires de Mathématiques.

Voir aussi : Une figure pleine de ressources et Histoires de Grecs

Introduction

Depuis 3 ans déjà, nous sommes quelques professeurs de mathématiques à nous être associés pour faire vivre au lycée Portes de l’Oisans de Vizille, un laboratoire de mathématiques consacré à l’histoire de notre discipline. Le choix de ce sujet a notamment été impulsé par les nouveaux programmes du lycée, l’histoire des mathématiques y tenant une place beaucoup plus importante qu’auparavant.

Aucun membre du laboratoire n’étant spécialiste de cette discipline, nous avons demandé l’aide d’un universitaire, Bernard Ycart, qui a travaillé sur ce sujet. Nous avons tout de suite été conquis, mais surtout impressionnés par l’étendue de ses connaissances. Cela nous a permis de mesurer notre ignorance, ainsi que la pauvreté des manuels scolaires sur l’histoire des maths. En effet, dans la majorité d’entre eux, celle-ci n’est abordée que par le biais d’une date ou du nom d’un savant, et encore de façon très superficielle. Dans ces manuels, peu de référence aux sources et peu de réflexion sur l’histoire des concepts.

Conscients de ces carences, nous avons tenté de réfléchir, pour nos élèves, à des exercices ayant un cadre moins artificiel, ce qui n’a évidemment pas été chose facile.
D’une part, notre formation d’enseignants ne nous a pas permis d’avoir une vision d’ensemble de l’histoire des mathématiques, celle-ci étant étroitement liée à l’Histoire. Il nous a donc paru nécessaire de faire apparaître ce lien auprès de nos élèves, afin de rendre vivant notre discours en classe par des anecdotes.

D’autre part, comme tout historien qui se penche sur des textes, la compréhension de la langue, ou plutôt l’incompréhension de la langue, est un premier barrage. Mais c’est surtout la façon d’aborder les problèmes qui n’est plus la même. Par exemple, aujourd’hui, la puissance de notre algèbre littérale a totalement balayé la vision purement géométrique qu’avaient les Anciens.

Les objets d’étude étant inépuisables, nous avons dû faire un choix. Le thème retenu, « Promenade historique autour de √2 » peut paraître réducteur ; il n’en est rien, au contraire ! Il permet de visiter de nombreuses périodes historiques et d’aborder les principaux domaines des mathématiques : géométrie, algèbre, analyse, algorithmique,… Enfin, il pourrait être envisagé comme fil conducteur tout au long de la classe de seconde, pour illustrer le programme d’un point de vue historique.

Dans ce qui suit, nous proposons une liste d’exercices, le plus souvent adaptés au niveau seconde, pour illustrer ce qui pourrait être fait avec des élèves. Il n’est pas difficile de créer une séance cohérente sur l’histoire des maths en piochant quelques exercices dans cette liste. La plupart de ces exercices ont été testés en classe.

Nous avons essentiellement utilisé deux sources : la personne de Bernard, intarissable conteur qui vous fait voyager d’une période à une autre, et d’une contrée à l’autre, en un claquement de doigts ; et son site, hist-math.fr, qui a été pour nous une mine quasiment illimitée d’informations. Nous tenons à le remercier pour sa gentillesse, sa générosité, sa disponibilité, et son aide précieuse dans la contextualisation des exercices. Cette aventure n’aurait clairement pas été la même sans lui !

Les exercices proposés ont été classés par thème et par ancienneté, plutôt que par difficulté. Les quatre premiers portent sur des algorithmes d’approximation, de la méthode de Héron aux fractions continues. On trouve ensuite trois démonstrations de l’irrationalité, dont deux démonstrations arithmétiques, en commençant par la plus ancienne, déjà connue d’Aristote avant Euclide. Ensuite, on propose dans un cadre simplifié une version de la démonstration par anthyphérèse que l’on trouve chez Euclide.
Viennent après deux exercices de constructions géométriques, typiques de la géométrie grecque, qui utilisent les propriétés de la hauteur d’un triangle rectangle. Nous terminons par un exercice d’optimisation.

Exercice 1. Lecture d’une tablette babylonienne : la plus ancienne trace du nombre √2.
Cet exercice, pour les élèves de seconde, permet la lecture et la compréhension d’un document archéologique où apparaît le nombre √2 . La principale difficulté consiste à comprendre comment fonctionne la numération babylonienne.

La tablette YBC7289 ci-contre, issue des collections de l’université de Yale, fut écrite au début du 2e millénaire avant J.C. dans le sud de l’Irak actuel. C’est une tablette de « constantes » écrite en numération babylonienne. Dans cet exercice, on cherche à comprendre ce qui est écrit sur la tablette.

 

1. Sur le site hist-math.fr, écouter la diapositive 9 de l’histoire « Le scandale des irrationelles ».
2. Placer sur une frise chronologique et une carte les Mésopotamiens.
3. La tablette YBC7289 est écrite en numération mésopotamienne qui est un peu différente de notre numération actuelle : elle repose sur un système de base 60 !
    
   
   Exemple 1 : La suite de caractères représente le nombre 23.
    
   
   Exemple 2 : Pour écrire 11 473, on pouvait écrire :

   En effet, 3×60²+11×60+13=11473.

   Nombre de soixantaines de soixantaines	Nombre de soixantaines	Nombre d’unités
   602	60	1

    

   • a. Écouter la diapositive 22 de l’histoire « Où tout a commencé ».
   • b. Comment s’appellent les symboles sur lesquels repose la numération mésopotamienne ?
   • c. Que représente le nombre  ?
   • d. Écrire en numération babylonienne le nombre 20147.
   • e. De la même façon, les Mésopotamiens savaient noter des nombres à virgule. Il leur suffisait de donner le nombre de paquets de ¹⁄₆₀, de ¹⁄_60², « contenus » dans le nombre à écrire. Écrire en écriture décimale le nombre représenté dans le tableau ci-dessous.
      
     

     Nombre de soixantaines de soixantaines	Nombre de soixantaines	Nombre d’unités	Nombre de soixantièmes	Nombre de soixantièmes de soixantièmes	Nombre de soixantièmes de soixantièmes de soixantièmes
     602	60	1	1⁄60	1⁄602	1⁄603

    

4. Synthèse. Sur la tablette YBC7289, on peut lire trois nombres A, B et C donnés par le tableau ci-dessous.
    
   

   	Nombre d’unités	Nombre de soixantièmes	Nombre de soixantièmes de soixantièmes	Nombre de soixantièmes de soixantièmes de soixantièmes
   Nombre	1	1⁄60	1⁄602	1⁄603
   A
   B
   C

    

   • a. Écrire ces trois nombres en écriture décimale (donner les valeurs exactes, puis arrondies à 10⁻⁹ près).
   • b. Vérifier que A × C ≃ B. Que représentent ces trois nombres sur le carré ?
   • c. À quelle précision les Mésopotamiens connaissaient-ils le nombre √2 ?

Cet exercice donne une vision simplifiée de la numération mésopotamienne. En fait, ce système ne notait pas les nombres exactement, mais seulement à une puissance de 60 près. Ainsi, pouvait désigner aussi bien 30 que 30×60, 30×60², ou bien ³⁰⁄₆₀ = ¹⁄₂, comme ici.

Exercice 2. Des identités remarquables.
Cet exercice, adapté au niveau seconde, permet de découvrir une 4^e identité remarquable.

Partie A. Sur la figure ci-contre, a et b représentent des longueurs de côtés, avec a>b. En écrivant l’aire totale de la figure de deux façons différentes, établir une égalité reliant a et b. on donne a+b = 12 et ab = 20. Déterminer a−b, puis les valeurs de a et b.

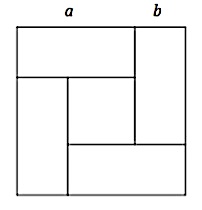Partie B.

1. « Le double du produit de deux nombres, ajouté à la somme de leurs carrés est égal au carré de leur somme. »
   Traduire cette phrase par une égalité algébrique.
2. Faire une figure permettant de retrouver cette égalité géométriquement.
3. Retrouver cette égalité en utilisant la double distributivité.

Exercice 3. Calcul d’une valeur approchée de √2 à l’aide de l’algorithme de Héron.
Tout comme l’exercice 4 ci-après, cet exercice, adapté au niveau seconde, permet le calcul à l’aide de Python d’une valeur approchée de √2 .

1. Placer Héron d’Alexandrie sur une frise chronologique et sur une carte.
2. À l’aide d’internet, compléter les deux définitions suivantes.
   • Quarrer : déterminer un ………… de même ………… qu’une figure délimitée par une courbe fermée.
   • Itérer : ………… plusieurs fois un même processus
3. On considère un premier rectangle de côtés ℓ=1 et L=2. On cherche à quarrer ce rectangle.
   • a. Quel serait le côté d’un carré de même aire que ce rectangle ?
   • b. Pour quarrer « petit à petit » ce rectangle, on considère le rectangle de même aire que le carré et dont la largeur ℓ’ mesure la moyenne de ℓ et de L. Quelle doit alors être la longueur L’ de ce 2^e rectangle ?

   

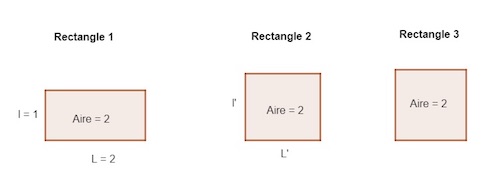
4. On considère maintenant le 2^e rectangle de côtés ℓ’ et L’.
   • a. Itérer le processus décrit dans la question 3b) et l’appliquant au 2^e rectangle.
   • b. Compléter le tableau ci-dessous avec les valeurs exactes puis arrondies à 10⁻⁹ près. Combien de décimales exactes du nombre √2 obtient-on ?
      

     	Largeur ℓ	Longueur L
     Rectangle 1	1	2
     Rectangle 2
     Rectangle 3

    

5. On considère l’algorithme de Héron ci-dessous écrit en version Python.

   L’algorithme permet de donner un encadrement du nombre √2. a. Implémenter ce programme sur EduPython. b. Pour combien d’itérations (pour quelle valeur de n) obtient-on : toutes les décimales de √2 de la calculatrice ? toutes les décimales de √2 connues par les Mésopotamiens ?

Exercice 4. Développement de √2 en fraction continue.
Cet exercice aborde un moyen efficace pour calculer une valeur approchée du nombre √2 . Il peut être vu en seconde, comme un exercice faisant le lien entre les maths et l’algorithmique. Mais il peut aussi tout à fait être envisagé en première lorsque la notion de suite est abordée.

Le but de cet exercice est de déterminer une approximation de racine de 2. On note x le réel défini par x = √2−1.

1. Démontrer que x est strictement compris entre 0 et 1.
2. En partant de √2 = 1+x, justifier chacune des étapes suivantes :
   • a. 2 = 1+2x+x²
   • b. 1 = x(2+x)
   • c.

     x =	1
     	2+x

3. En déduire chacune des étapes suivantes :
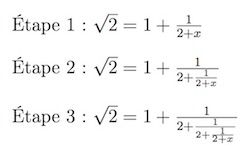
4. On considère la fonction suivante, écrite en langage Python :

   Programmer cet algorithme. Que renvoie approx(4) ?

5. Une calculatrice donne 1,414213562 pour valeur approchée de √2. À l’aide de la fonction précédente, déterminer la plus petite valeur de n qui permet d’obtenir les mêmes 9 premières décimales. Cette méthode d’approximation vous semble-t-elle efficace ?

Pistes d’histoire : À l’aide des découpages de surfaces évoqués dans l’exercice 2, les Mésopotamiens manipulaient couramment nos identités remarquables et ils savaient résoudre des équations du second degré, comme raconté dans « Les pères de l’algèbre ». Il est d’ailleurs probable que des découpages du type de ceux de l’exercice 2, soient à l’origine de l’algorithme de Héron (exercice 3), et de l’approximation notée sur la tablette YBC7289 (exercice 1). Ces hypothèses sont évoquées dans « De Babylone ou d’ailleurs ». La fin de cette même histoire porte sur les fractions continues, qui font l’objet de l’exercice 4. Il est question de YBC7289, également dans « La maison des tablettes ».

Exercice 5. Irrationalité de √2 par la parité.
Cet exercice propose la première démonstration arithmétique connue de l’irrationalité de √2 . Elle est plus sophistiquée que celle de l’exercice suivant, et pourrait être proposée aux élèves de terminale ayant choisi l’option Maths expertes.

Rappel préalable. Toute fraction admet une écriture irréductible. Autrement dit, toute fraction admet une écriture ^a⁄_b où a et b sont deux entiers premiers entre eux, c’est-à-dire qu’ils n’ont pas d’autres diviseurs communs que −1 et 1.

1. n désignant un entier relatif, démontrer l’implication : si n² est pair, alors n est pair.
   Indication  : Démontrer la contraposée de cette implication et conclure.
2. Démonstration de l’irrationalité de √2 à l’aide d’un raisonnement par l’absurde.
   Supposons donc que √2 soit un nombre rationnel. Cela signifie que √2 = ^a⁄_b, où a et b sont deux entiers relatifs premiers entre eux, b étant non nul.
   • a. Démontrer que a² est pair. Qu’en déduit-on sur a ?
   • b. Démontrer qu’alors b est pair.
   • c. Conclure.

Exercice 6. Autre démontration arithmétique de l’irrationalité de √2.
La démonstration qui suit de l’irrationalité de √2 (inscrite dans le programme de seconde) est tout à fait adaptée au niveau seconde.

Rappel préalable. Toute fraction admet une écriture irréductible. Autrement dit, toute fraction admet une écriture ^a⁄_b où a et b sont deux entiers premiers entre eux, c’est-à-dire qu’ils n’ont pas d’autres diviseurs communs que −1 et 1.

1. Démonstration de l’irrationalité de √2 à l’aide d’un raisonnement par l’absurde.
   Supposons donc que √2 soit un nombre rationnel. Cela signifie que √2 = ^a⁄_b, où a et b sont deux entiers relatifs premiers entre eux, b étant non nul.
   • a. Justifier alors que 2b² = a². Info : Si deux nombres sont égaux, alors leurs carrés sont égaux.
   • b. Compléter les tableaux suivants :
      

     Si le chiffre des unités de a est :	0	1	2	3	4	5	6	7	8	9
     alors le chiffre des unités de a2 est :					6

      

     Si le chiffre des unités de b est :	0	1	2	3	4	5	6	7	8	9
     alors le chiffre des unités de b2 est :					6
     donc le chiffre des unités de 2b2 est :					2

     
     

   • c. Déduire le(s) chiffre(s) des unités possible(s) de a et b quand 2b² = a².
   • d. Quelle contradiction obtient-on ? Qu’en déduit-on pour le nombre √2 ?

   Info : On peut démontrer de façon analogue que √3, √5, √6, √7, √8 … ne sont pas des nombres rationnels. Plus généralement, on peut retenir que si n est un entier naturel mais pas un carré parfait, alors √n n’est pas un nombre rationnel.

2. Pour aller plus loin : Piste rouge pour ceux qui se sentent à l’aise.
   • a. Démontrer, en raisonnant par l’absurde, que le nombre (3√2+7) ⁄ 5 n’est pas un rationnel.
   • b. Plus généralement, démontrer que, quels que soient les entiers relatifs p, q et r avec p≠0 et r≠0, le nombre (p√2+q) ⁄ r n’est pas un nombre rationnel.
   • c. Justifier que 3√2, √2−4, √2 ⁄ 5 et (−√2−3) ⁄ 2 ne sont pas rationnels.

Ou bien :

3. Pour aller plus loin : Piste bleue pour ceux qui se sentent moins à l’aise.
   Démontrer, en raisonnant par l’absurde, que les nombres 3√2, √2−4 et (3√2+7) ⁄ 5 ne sont pas rationnels.

Exercice 7. Irrationalité de √2 : démonstration géométrique.
Cet exercice a été construit à partir du document d’accompagnement du programme de seconde. Plus originale que les démonstrations arithmétiques, cette démonstration de l’irrationalité de √2 n’est pas « facile » mais elle aborde des choses de manière intéressante car géométrique.

Le but de cet exercice est de démontrer géométriquement que √2 n’est pas un nombre rationnel, en raisonnant par l’absurde.

1. Compléter les pointillés :
   Supposons que √2 est un nombre rationnel. Il existe donc deux entiers naturels p et q premiers entre eux, avec q<p, tels que √2 = … ⁄ …, ce qui équivaut à p = …
2. On construit un triangle ABC isocèle rectangle en B tel que AB = q .
   • a. Calculer la longueur AC en fonction de q puis l’exprimer en fonction de p.

     L’hypothèse faite dans la question 1 revient à supposer que le triangle ABC est le plus petit triangle rectangle isocèle dont les longueurs des côtés sont des nombres entiers naturels. Soit D le point tel que ABCD soit un carré. Soit B’ le point du segment [AC] qu’on obtient en repliant le côté [AD] sur le segment [AC]. Soit A’ le point du segment [CD] qu’on obtient par ce pliage. La droite (AA’) est alors axe de symétrie du quadrilatère AB’A’D.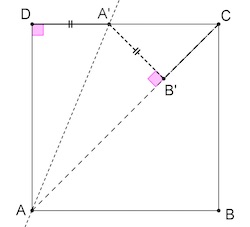

   • b. Construire et découper un carré puis effectuer le pliage ci-dessus.
   • c. En raisonnant sur les angles, démontrer que le triangle A’B’C est isocèle et rectangle en B’.
   • d. Exprimer la longueur CB’ en fonction de p et q.
   • e. Démontrer que A’C = 2q−p.
   • f. En déduire que √2 peut s’écrire sous la forme p’ ⁄ q’, où p’<p et conclure.

Pistes d’histoire : Le fait que la diagonale d’un carré n’est pas commensurable avec le côté de ce carré a été découvert très tôt par les Grecs : c’est ce que l’on appelle « Le scandale des irrationnelles », ou encore « scandale pythagoricien ». La démonstration arithmétique de l’exercice 5 est une des plus anciennes. Elle est citée plusieurs fois par Aristote. Euclide, lui, applique l’algorithme des différences : deux longueurs étant données, si on retranche la plus petite de la plus grande de façon itérée, l’algorithme se termine en un nombre fini d’étapes si et seulement si les deux grandeurs sont commensurables. Cette technique, baptisée anthyphérèse, est formalisée en une démonstration par l’absurde dans l’exercice 7. Voir aussi « Une figure pleine de ressources ».

Exercice 8. Quadrature d’un rectangle.
Cet exercice est adapté au niveau seconde et nécessite l’usage d’un ordinateur et du logiciel Geogebra. Sa réalisation complète demande plus d’une heure de cours.

Info : Réaliser la « quadrature d’une figure plane » consiste à construire, à la règle et au compas, un carré ayant la même aire que la figure donnée.

1. Exemples
   • a. Construire un carré de même aire qu’un rectangle de largeur 2cm et de longueur 8cm.
   • b. Construire un carré de même aire qu’un rectangle de largeur 2cm et de longueur 6cm. Quelle difficulté rencontre-t-on ?
2. Dans les Éléments, livre 2, proposition XIV, Euclide (vers 300 av. J.C.) propose un programme de construction pour réaliser, à la règle et au compas, la quadrature d’un rectangle.
   L’image ci-dessous montre la proposition dans une traduction de 1632.

   

   Voici la version moderne.

   ABCD est un rectangle tel que AB est supérieure à BC. Sur la demi-droite [AB) placer le point E tel que BE = BC. Construire le point I milieu de [AE], puis tracer un demi cercle de centre I passant par A. La droite (BC) coupe le demi-cercle tracé en un point F. Alors le carré BEFG a la même aire que le rectangle ABCD. Le but des questions suivantes est de contrôler la méthode d’Euclide.

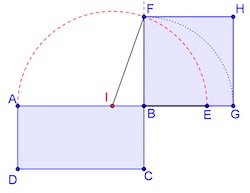
3. Appliquer le programme d’Euclide pour réaliser la quadrature du rectangle de la question 1b) et démontrer sa validité en justifiant que HB=√12 cm.
4. Réalisation de la figure à l’aide du logiciel Geogebra.
   • Afficher les axes d’un repère orthonormal.
   • Construire le point A(0 ;0).
   • Sur l’axe des abscisses, placer un point B d’abscisse positive.
   • Sur l’axe des ordonnées, placer un point D d’ordonnée négative.
   • Construire le point C de même abscisse que B et de même ordonnée que D (par C=(x(B),y(D))) dans la barre de saisie).
   • Sur la demi-droite [AB), construire le segment [BE] de longueur BC.
   • Construire le milieu I de [AE] (par I = MilieuCentre(A,E) dans la barre de saisie) puis le demi-cercle de diamètre [AE].
   • Construire la droite (CB) puis le point F intersection de (CB) avec le demi-cercle précédent.
   • Construire le carré de côté FB (en sélectionnant Polygone régulier) puis faire afficher son aire.
   • Déplacer B et/ou D et observer.
5. Une première démonstration, avec le théorème de Pythagore.
   Soient a et b deux réels non nuls tels que a>b, on considère le rectangle ABCD de longueur AB = a et de largeur BC = b.
   
   • Justifier que AI = IF.
   • Exprimer les distances IF et IB en fonction de a et b.
   • Justifier que le triangle IBF est rectangle en B puis déterminer la distance FB en fonction de a et b.
   • Conclure.
6. Une deuxième démonstration, avec des triangles semblables.
   
   • Quelle est la nature du triangle AEF ?
   • Justifier que les triangles ABF et FBE sont semblables.
   • En déduire que BF² = ab et conclure.

Exercice 9. Construction, à la règle et au compas, d’un segment de longueur √a.
Cet exercice, également destiné aux élèves de seconde, est en quelque sorte un cas particulier du précédent. Il propose aussi deux démonstrations du même résultat. La première permet notamment de travailler le calcul algébrique. La deuxième permet de travailler sur les triangles semblables.

1. Dans sa « Géométrie », René Descartes propose une construction à la règle et au compas, d’un segment de longueur √a, avec a réel strictement positif. Voici le passage dans l’édition originale de 1637.

   

   Voici la version moderne.

   Placer trois points A, B, C alignés dans cet ordre, tels que AB = a et BC = 1. Construire le point I milieu de [AC], puis tracer un demi-cercle de centre I passant par A. La perpendiculaire à [AC] passant par B coupe le demi-cercle tracé en un point D. Alors le segment [BD] a une longueur égale à √a. Le but des questions suivantes est de contrôler la méthode de Descartes.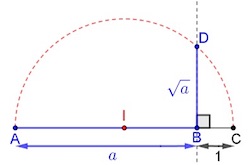

2. Appliquer le programme de Descartes pour construire un segment de longueur √2.
3. Une première démonstration, avec le théorème de Pythagore.
   • Justifier que AI = ID.
   • Exprimer les distances ID et IB en fonction de a.
   • En déduire que BD² = a et conclure.
4. Une deuxième démonstration, avec des triangles semblables.
   • Quelle est la nature du triangle ACD ?
   • Justifier que les triangles ABD et DBC sont semblables.
   • En déduire que BD² = a et conclure.

Pistes d’histoire : Les problèmes de quadrature comptent parmi les plus anciens raisonnements géométriques de l’histoire. L’acharnement sur la quadrature du cercle est à l’origine d’une bonne partie des mathématiques actuelles : voir « La fin du suspense » et chercher « quadrature » dans la barre de recherche de hist-math.fr. Le problème de quadrature le plus ancien est la duplication du carré, que Platon fait expliquer par Socrate dans le Ménon. C’est un cas particulier du théorème de Pythagore : voir « La chaise de la mariée ». Les deux exercices 8 et 9 utilisent le même outil de base : dans un triangle rectangle, la hauteur issue de l’angle droit partage le triangle en deux triangles semblables. De là on déduit que sa longueur est la moyenne géométrique des deux segments qu’elle découpe sur l’hypoténuse. Le théorème de Pythagore « généralisé » en découle. « Les lunules d’Hippocrate » lui sont liées et peuvent fournir aussi des exercices intéressants au niveau lycée. Les multiples ramifications historiques sont évoquées dans « Une figure pleine de ressources », article déjà cité. Bien que l’énoncé de l’exercice 9 soit tiré de la Géométrie de Descartes, il est un cas particulier de la quadrature du rectangle qui fait l’objet de l’exercice 8, et qui est bien connue depuis les Grecs.

Exercice 10. Le tonneau de Kepler.
Dans cet exercice, une fonction est étudiée à l’aide de sa dérivée. Il ne peut donc pas être traité avant la classe de première.

À l’occasion de son mariage, Kepler (1571—1630) observe que la contenance des tonneaux de vin qu’il a achetés est évaluée à l’aide d’un instrument appelé « verle » qui mesure la longueur AI (voir figure-ci-dessous). Kepler cherche alors à trouver les dimensions du tonneau qui permettent d’avoir un volume maximal pour une longueur AI donnée. Voici la figure de Kepler dans son livre de 1615, et la version simplifiée que nous utiliserons.

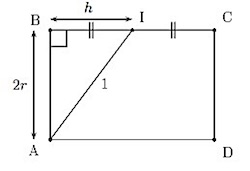On assimile le tonneau à un cylindre dont la base est un disque de rayon r et dont la demi-hauteur mesure h comme le montre la figure de droite, vue comme une coupe transversale du tonneau « couché ». On considère que la longueur AI est fixée et égale à 1, et on cherche alors les dimensions h et r du tonneau de plus grand volume, vérifiant 0 ≤ 2r ≤ 1 et 0 ≤ h ≤ 1.

Rappel : le volume d’un cylindre est le produit de l’aire de la base, multipliée par la hauteur.

Partie A : deux cas particuliers qui donnent des volumes différents.

1. 1^er cas : on choisit r = ¹⁄₄. Calculer h et en déduire le volume du tonneau.
2. 2^e cas : on choisit r = ¹⁄₃. Calculer le volume du tonneau dans ce deuxième cas.

Partie B : cas général.

1. Exprimer le volume du tonneau en fonction de h et de r.
2. En considérant le triangle ABI, exprimer r² en fonction de h².
3. Déduire des questions précédentes que le volume du tonneau est donné par la fonction V définie sur [0 ;1] par : V(h) = (^π⁄₄)(h−h³)
4. Déterminer V’(h). Quelle est la valeur de h qui permet d’obtenir un volume maximal ?
5. En utilisant l’égalité du 2., déterminer le rapport ^h⁄_r lorsque V atteint son maximum.

Pistes d’histoire : Le problème du tonneau a été le prétexte d’une de ces envolées aussi brillantes que révolutionnaires dont Kepler avait le secret. On peut considérer que « La stéréométrie des tonneaux de vin » a donné le coup d’envoi de l’analyse moderne au XVII^e siècle. La réussite de Kepler sur le problème d’optimisation qui fait l’objet de l’exercice 10, est d’autant plus remarquable que cela se passait vingt ans avant la méthode « De maximis et minimis » de Fermat, et un bon demi-siècle avant que Newton n’invente sa « Méthode des fluxions », c’est-à-dire nos dérivées.

Conclusion

Nous sommes loin d’avoir épuisé le sujet. En suivant le même fil conducteur de √2, de nombreuses autres pistes d’histoire auraient pu être explorées. Citons par exemple la forme des alvéoles d’abeilles, l’écartement des frettes sur un manche de guitare, la formule de Viète, entre autres.

Le bilan de notre expérience du laboratoire de mathématiques est mitigé. D’un côté il nous a permis d’échanger sur nos pratiques, de construire ensemble certains documents, de nous former un peu en histoire des mathématiques. À nos côtés dès le début, Bernard nous a été d’une aide précieuse et nous le remercions à nouveau. Nous remercions également les inspecteurs qui nous ont suivis lors de cette aventure.

Après trois ans d’existence du labo, nous ne cachons cependant pas une certaine déception. Tout comme n’importe quelle activité créatrice, elle nécessite du temps : du temps pour s’approprier des connaissances, du temps pour échanger, du temps pour entrevoir un début de structure, du temps pour élaborer les énoncés des exercices. Comme vous vous en doutez, durant ces trois ans, nous n’avons pas pour autant abandonné nos élèves. Nous avons continué, comme chaque enseignant, à préparer nos cours et à les dispenser, dans le cadre très lourd de la crise sanitaire, de l’enseignement hybride et de la réforme du lycée qui a encore accru notre charge de travail. Nous déplorons que la décharge hebdomadaire d’une demi-heure par semaine prévue initialement se soit finalement transformée, comme c’est souvent le cas, en quelques HSE. Cette décharge nous aurait permis de nous investir davantage dans cette activité ô combien enrichissante mais si peu prioritaire au regard de nos préoccupations quotidiennes.

Toutefois, nous sommes quelques-uns à envisager la poursuite de ce labo, toujours en histoire des maths car nous sommes passionnés par le sujet, et si Bernard reste à nos côtés bien entendu.