Cet article peut être librement diffusé à l’identique dans la limite d’une utilisation non commerciale suivant la licence CC-nc-nd
(http://creativecommons.org/licenses/by-nc-nd/3.0/fr/)
Dans cet article, je traite un exercice qui m’était proposé par un collègue. Cet exercice fait partie des problèmes de recherche de lieu dans l’espace.
Au début de mes recherches, je me suis interdit d’utiliser mon ordinateur et tout autre outil utilisant les T.I.C et en particulier les logiciels de géométrie dynamique, et bien, je reconnais que mes résultats n’étaient pas encourageants !
J’ai renoncé à ma décision et je me suis permis de me servir d’un logiciel de géométrie dynamique : GeoGebra5 qui m’a permis de :
- faire une figure
- énoncer une conjecture sur la nature et les éléments caractéristiques du lieu,
- infirmer ou confirmer certaines apparences remarquées sur la figure et qui peuvent représenter des éléments de base dans certaines étapes de mes démonstrations.
Énoncés
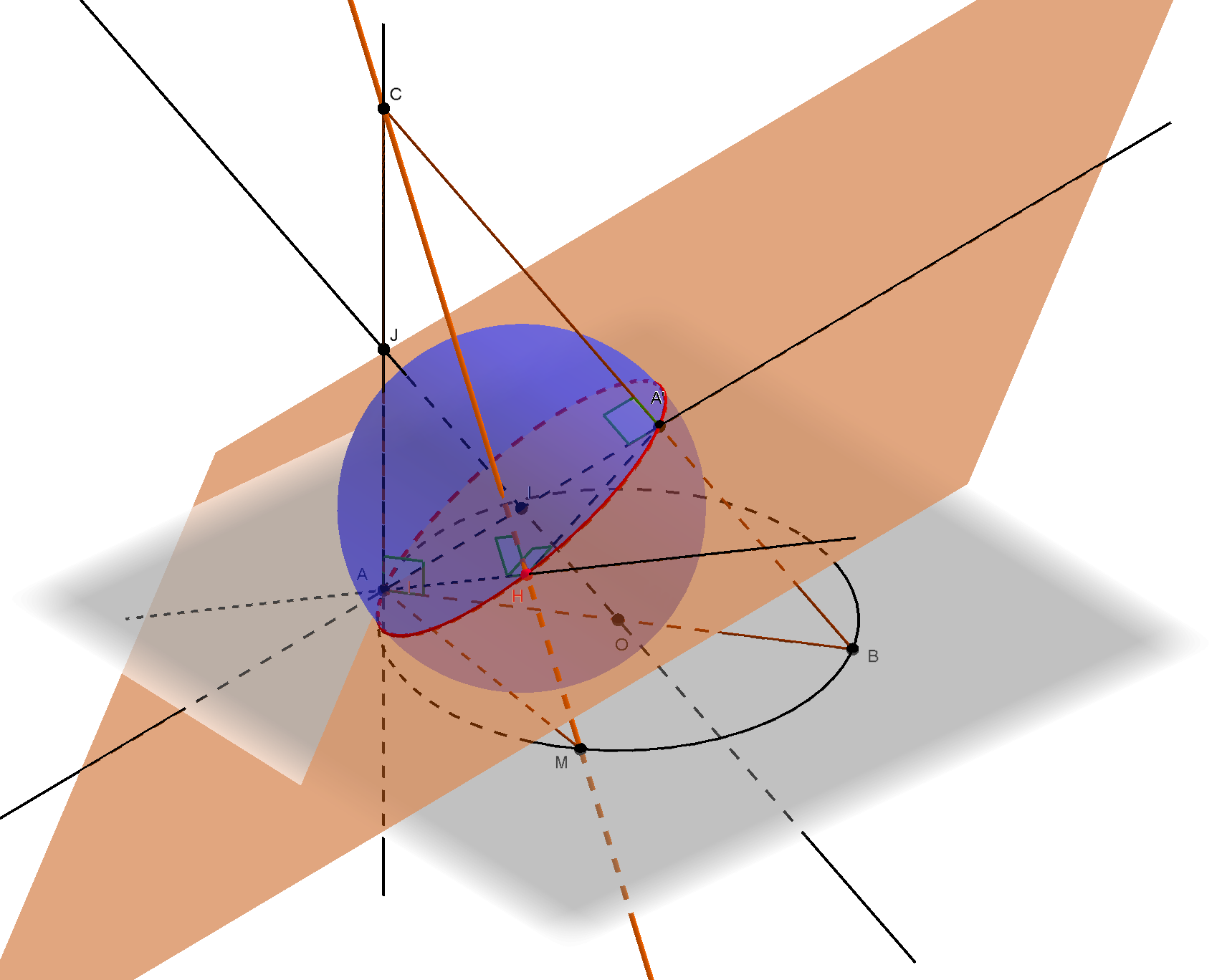
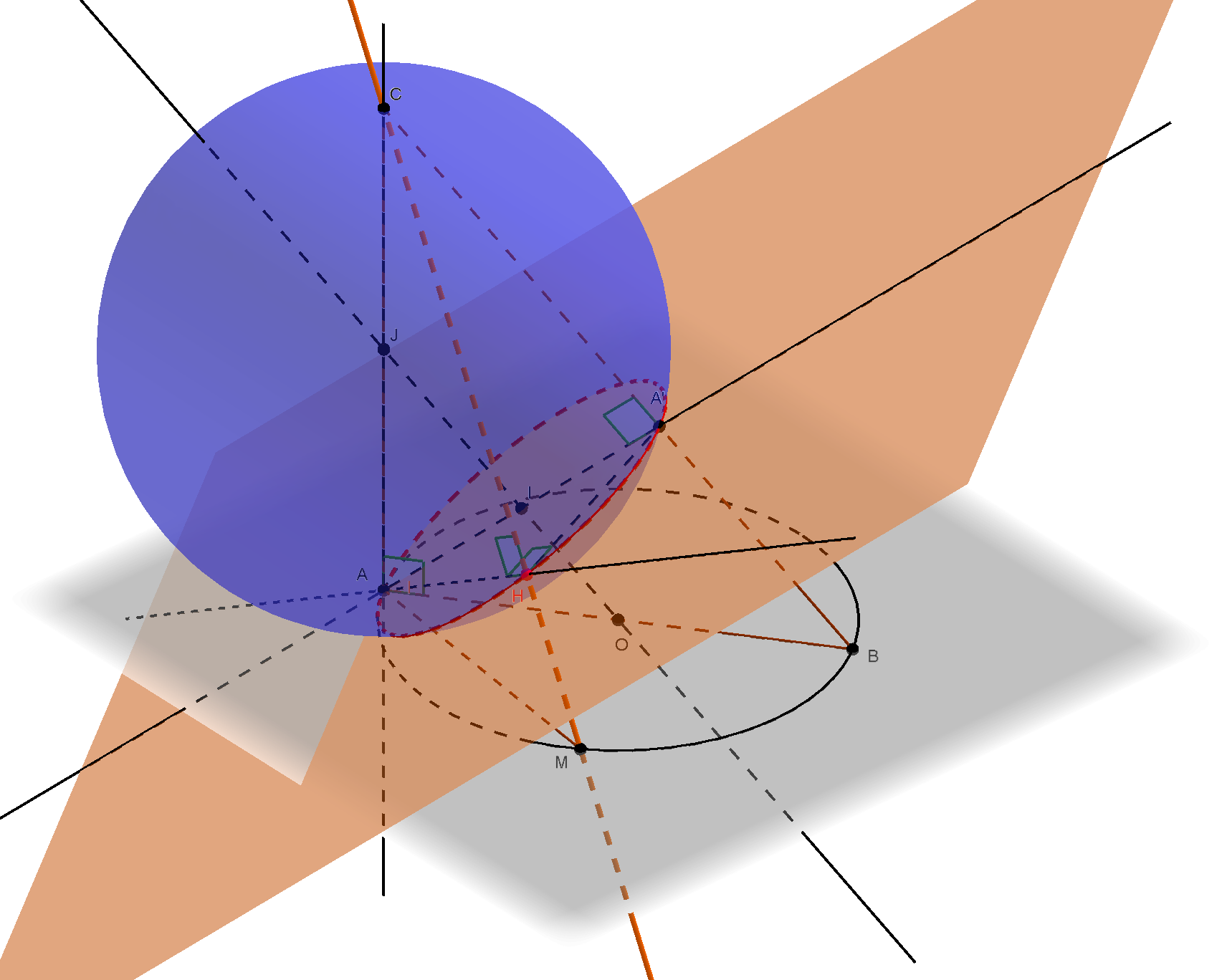
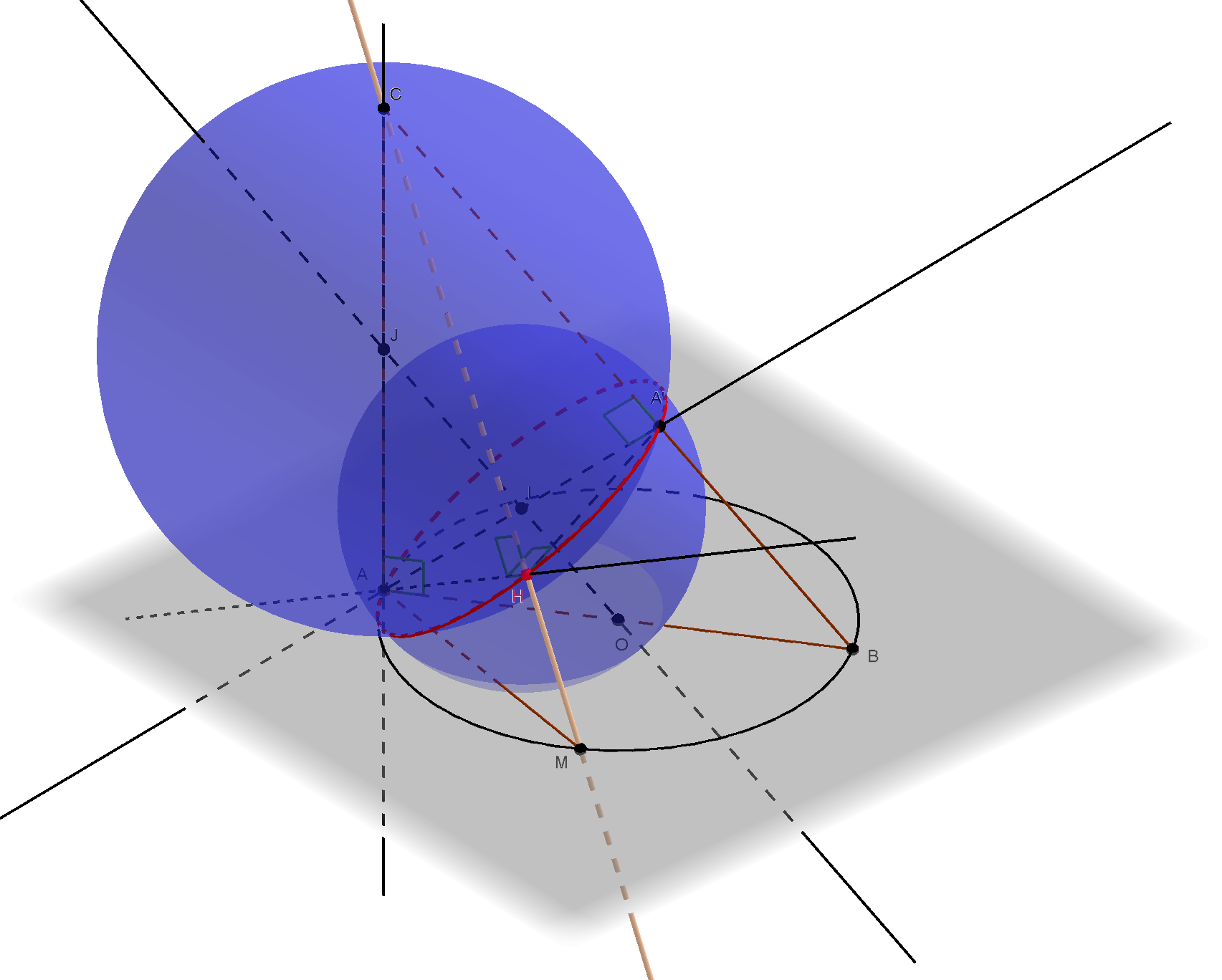
- $ABC$ un triangle rectangle en $A$,
- $(P)$ est le plan perpendiculaire à la droite $(AC)$ et passant par $A$,
- $\zeta$ est le cercle de diamètre $[AB]$ contenu dans $(P)$,
- $M$ est un point variable sur le cercle $\zeta$,
- $H$ est le projeté orthogonal de $A$ sur $(CM)$.
On se propose de trouver sur quelle ligne varie $H$ lorsque $M$ varie sur $\zeta$.
- En utilisant un logiciel de géométrie de l’espace :
- Réaliser une figure,
- Déplacer $M$ et observer la trajectoire du point $H$,
- Émettre une conjecture sur la nature du lieu de $H$,
- Démontrer la conjecture.
(Problème de lieu page 161 du Tome 2 du manuel Tunisien de la 2e Sciences)
Solution
- Figure : Voir vidéo Youtube
- Trajectoire du point $M$ : Voir vidéo Youtube
- Conjecture sur la nature du lieu de $H$ : le lieu de $H$ est le cercle de diamètre $[AA’]$ inclus dans le plan perpendiculaire à $(BC)$ en $A’$ ($A’$ : le projeté orthogonal de $A$ sur $(BC)$) :
- Voir vidéo Youtube
- Vérification de la conjecture : Voir vidéo Youtube
Dans toute la suite, on désignera par :
- $A’$ : le projeté orthogonal de $A$ sur $(BC)$
- $I$ : le milieu de $[AA’]$
- $(Q)$ : le plan $(BCM)$ (lorsque $M \neq B$)
Propositions
Cette partie est présentée sous forme de blocs ouvrables et refermables.
Proposition 2 : Intersection plan et sphère
1re étape
On reprend la 1re étape de la proposition 1.
On en retient que : Pour tout point $M$ du cercle $\zeta$, $H$ appartient au plan $(R)$ perpendiculaire à la droite $(BC)$ en $A’$
2e étape
D’après la 1re étape, $H$ est le projeté orthogonal de $A$ sur $(Q)$
$$\left. \begin{array}{c} \text{alors }(AH)\perp (Q) \\ \text{et on a }(A^{\prime }H)\subset (Q) \end{array} \right\} \Longrightarrow (AH)\perp (A^{\prime }H)\Longrightarrow \widehat{AHA^{\prime }}=90º$$
alors $H$ appartient à la sphère $S$ de diamètre $[AA’]$, soit $I$ son centre.
Résumé
Pour tout point $M$ du cercle $\zeta$, on a :
$$\left. \begin{array}{c} H \in (R)\text{ : plan fixe qui contient }A \text{ et }A^{\prime } \\ H \in \text{sphère }S \text{ de centre }I \text{ et de rayon }IA \end{array} \right\} \Longrightarrow (H \in S_{(I,IA)} \cap (R)$$
3e étape
Nature de : $S_{(I,IA)} \cap (R)$
$A$ et $A’$ sont deux points de $(R)$
alors le point $I$ = $A \ast A’$ est un point de $(R)$ ($d(I,(R)) = 0 < IA$)
donc la sphère $S_{(I,IA)}$ et le plan $(R)$ se coupent suivant le cercle de centre $I$ et de rayon $IA$ inclus dans ce plan
Conclusion
Quand $M$ varie sur $\zeta$, $H$ décrit le cercle de diamètre $[AA’]$ du plan $(R)$ perpendiculaire à $(BC)$ en $A’$.
- Lieu de H
- Quand $M$ varie sur $\zeta$, $H$ décrit le cercle de diamètre $[AA’]$ du plan $(R)$ perpendiculaire à $(BC)$ en $A’$.
Proposition 3 : Intersection plan et sphère
1re étape
On reprend la 1re étape de la proposition 1.
On en retient que : Pour tout point $M$ du cercle $\zeta$, $H$ appartient au plan $(R)$ perpendiculaire à la droite $(BC)$ en $A’$
2e étape
$H$ est le projeté orthogonal de $A$ sur $(CM)$
$\Longrightarrow (AH)\perp (CH)\Longrightarrow \widehat{AHC}=90º$
alors $H$ appartient à la sphère $S’$ de diamètre $[AC]$, soit $J$ son centre.
Résumé
Pour tout point $M$ du cercle $\zeta$, on a :
$\left.
\begin{array}{c}
H \in (R) \text{ : plan fixe qui contient }A \text{ et }A^{\prime} \\
H \in (R) \text{ sphère }S^{\prime} \text{ de centre }J \text{ et de rayon }JA
\end{array} \right\}$
3e étape
Nature de : $S^{\prime}_{(J,JA)} \cap (R)$
Sous-étape 3.1
On a : $\left.
\begin{array}{c}
H \text{est le projeté orthogonal de }A \text{ sur }(Q) \\
\Longrightarrow (AH) \perp (Q) \\
\text{et on a }(CA^{\prime})\subset(Q)
\end{array} \right\} \Longrightarrow (CA^{\prime}) \text{ est orthogonal à }(AH)$
et $A^{\prime}AC$ rectangle en $A^{\prime} \Longrightarrow (CA^{\prime}) \perp (AA^{\prime})$
et puisque $(AA’)$ et $(AH)$ sont deux droites sécantes du plan $(R)$, on aura $(CA’)$ perpendiculaire à $(R)$
$\left. \begin{array}{c} (CA^{\prime}) \perp (R) \\ (HI) \subset(R) \end{array} \right\} \Longrightarrow (CA^{\prime}) \text{ est orthogonal à }(IH)$
D’autre part, on a : $\left. \begin{array}{c} A^{\prime}AC \text{ triangle} \\ I=A \ast A^{\prime} \\ J=A \ast C \end{array} \right\} \Longrightarrow (IJ)//(CA^{\prime})$
ainsi : $\begin{equation} \left. \begin{array}{c} (CA^{\prime}) \text{ est orthogonale à }(IH) \\ (CA^{\prime})//(IJ) \end{array} \right\} \Longrightarrow (IJ) \perp (IH) \end{equation} \qquad :(1)$
on a aussi : $\begin{equation} \left.
\begin{array}{c}
A^{\prime}AC \text{ rectangle en }A^{\prime} \\
(CA^{\prime})//(IJ)
\end{array} \right\} \Longrightarrow (IJ) \perp (AA^{\prime}) \text{ en }I \end{equation} \qquad :(2)$
et $\begin{equation}(IJ) \text{ et }(AA^{\prime}) \text{ sont deux droites sécantes du plan }(R) \end{equation} \qquad :(3)$
de $(1)$,$(2)$ et $(3)$, on déduit que $I$ est le projeté orthogonal de $J$ sur $(R)$
alors la distance de $J$ à $(R)$ est $IJ$ : $d(J,(R))=IJ$
Sous-étape 3.2
Le triangle $A^{\prime}AC$ est rectangle en $A^{\prime}$
$\Longrightarrow CA^{\prime} < CA$
$\Longrightarrow \frac{CA^{\prime}}{2} < \frac{CA}{2}$
$\Longrightarrow JI < JA$
$\Longrightarrow d(J,(R)) < JA$
Conclusion
La sphère $S^{\prime}_(J,JA)$ et le plan $(R)$ se coupent suivant le cercle de centre $I$ : projeté orthogonal de $J$ sur $(R)$ et de rayon $IA$ : lieu des points $H$. ($A$ appartient à ce cercle car si $M = A$ on aura $M = A = H$)
Quand $M$ varie sur $\zeta$, $H$ décrit le cercle de diamètre $[AA’]$ du plan $(R)$ perpendiculaire à $(BC)$ en $A’$
- Intersection Plan/Sphère
- Intersection de la sphère $S_(J,JA)$ et du plan $(R)$
Proposition 4 : Intersection de deux sphères
1re étape
On reprend la 1re étape de la proposition 1.
On en retient que : Pour tout point $M$ du cercle $\zeta$, $H$ appartient au plan $(R)$ perpendiculaire à la droite $(BC)$ en $A’$
2e étape
D’après la 1re étape, $H$ est le projeté orthogonal de $A$ sur $(Q)$
$\left.
\begin{array}{c}
\text{alors }(AH)\perp (Q) \\
\text{et on a }(A^{\prime }H)\subset (Q)
\end{array}
\right\} \Longrightarrow (AH)\perp (A^{\prime }H)\Longrightarrow \widehat{AHA^{\prime }}=90º$
alors $H$ appartient à la sphère S de diamètre$[AA’]$, soit $I$ son centre.
3e étape
$H$ est le projeté orthogonal de $A$ sur $(CM)$
$\Longrightarrow (AH)\perp (CH)\Longrightarrow \widehat{AHC}=90º$
alors $H$ appartient à la sphère $S’$ de diamètre $[AC]$, soit $J$ son centre.
4e étape
Rappelons la règle :
Si deux sphères $S_{(O,r)}$ et $S^{\prime}_{(O^{\prime},r^{\prime})}$ sont telles que $\left \vert r-r^{\prime} \right \vert < OO^{\prime} < r+r^{\prime}$ alors elles se coupent suivant un cercle d’axe $(OO’)$ et dont le centre $K$ vérifie $2\overrightarrow{LK}\cdot \overrightarrow{OO^{\prime }} = r^{2}-r^{\prime 2}$(où $L = O \ast O^{\prime}$)
Dans notre situation :
$AIJ$ est un triangle dont la mesure du côté :
- $[IJ]$ est la distance entre les centres des sphères $S$ et de $S’$
- $[AI]$ est le rayon de $S$
- $[AJ]$ est le rayon de $S’$
On a : $\left\vert AI-AJ\right\vert < IJ < AI+AJ$ (AIJ triangle)
$\left\vert r-r^{\prime}\right\vert < IJ < r+r^{\prime}$
alors $S$ et $S’$ se coupent suivant un cercle d’axe $(IJ)$ et dont le centre $K$ vérifie :
$2\overrightarrow{LK}\cdot \overrightarrow{IJ}=r^{2}-r^{\prime 2}$ ($L=I \ast J$)
$\Longrightarrow 2\overrightarrow{LK}\cdot \overrightarrow{IJ}=\overrightarrow{AI}^{2}-\overrightarrow{AJ}^{2}$
$\Longrightarrow 2\overrightarrow{LK}\cdot \overrightarrow{IJ}=\left(\overrightarrow{AI}-\overrightarrow{AJ}\right)\left(\overrightarrow{AI}+\overrightarrow{AJ}\right)$
$\Longrightarrow 2\overrightarrow{LK}\cdot \overrightarrow{IJ}=2\overrightarrow{JI}\cdot \overrightarrow{AL}$
$\Longrightarrow 2\overrightarrow{LK}\cdot \overrightarrow{IJ}-2\overrightarrow{JI}\cdot \overrightarrow{AL}=0$
$\Longrightarrow 2\overrightarrow{AL}\cdot \overrightarrow{IJ}=0$
$\left.
\begin{array}{c}
\overrightarrow{AL}\cdot \overrightarrow{IJ}=0 \\
\overrightarrow{AL} \neq \overrightarrow{0} \text{ et } \overrightarrow{IJ} \neq \overrightarrow{0}
\end{array}
\right\} \Longrightarrow (AL)\perp (IJ) \qquad :(1)$
A ce niveau, rappelons que : $\left.
\begin{array}{c}
(IJ)//(BC)=(CA^{\prime}) \\
\text{et }(AA^{\prime}) \perp (CA^{\prime})
\end{array}
\right\} \Longrightarrow (AA^{\prime})\perp (IJ)$
$\Longrightarrow (AI) \perp (IJ)$ en $I$ ($I=A \ast A^{\prime}) \qquad :(2)$
D’après $(1)$ et $(2)$, on déduit que $L=I$
Conclusion
Le point $H$ décrit le cercle passant par $A$ et ayant pour centre $I$ et pour axe $(IJ)$
- Intersection Sphère/Sphère
- Le point $H$ décrit le cercle passant par $A$ et ayant pour centre $I$ et pour axe $(IJ)$
Conclusion
« La situation de blocage dans laquelle je m’étais trouvé avant de me servir du logiciel, ainsi que le collègue qui m’a proposé l’exercice (et qui est d’ailleurs de ma génération) reflète une défaillance dans notre formation en géométrie dans l’espace.
Mais la question reste pour moi :
- « Est-ce que cette défaillance est due à nous-mêmes ou aux programmes qu’on nous a enseignés durant notre cursus scolaire et universitaire ? »
- « Pourquoi nos prédécesseurs ne souffraient pas autant malgré la pauvreté de leur époque en T.I.C ? »
Peut-être la réponse à ma question servira d’outil pour fixer une stratégie adéquate qui conciliera les enseignants et leurs élèves avec l’enseignement de la géométrie dans l’espace. (Je ne parle pas de la géométrie analytique). »
Documents Annexes
Vidéos embarquées
- Vidéo nº1 : Réalisation de la figure
- Construction pas à pas de la figure à l’aide de Géogébra5 (Version 3D).
Durée 10min 32s.
- Vidéo nº2 : Trajectoire du point H.
- Mise en évidence de la trajectoire du point $H$ à l’aide de Géogébra 3D.
Durée 3min 01s.
- Vidéo nº3 : Construction du lieu de H
- Construction pas à pas du lieu de $H$ avec Géogébra5 3D.
Durée 5min 35s.
- Vidéo nº4 : Vérification du lieu de H
- Suite et fin de la construction 3D pas à pas avec Géogébra5
Durée 3min 52s.
Fichier Géogébra 5
- Fichier Géogébra5 de la figure en 3D
- Fichier 3D Géogébra5
Article original en pdf
- Article original
- Cet article en pdf dans sa version originale rédigée par l’auteur.
Hédi Abderrahim
Ndrl : Alexandre Brouillaud a ajouté à l’article d’Hédi Abderrahim des vidéos et une figure GeoGebra.