Autres contributions de Gilles Aldon dans MathémaTICE

TP Maple, π ou un voyage dans l’histoire des maths

L’article au format pdf.

Cet article reprend et rend compte d’un TP proposé dans le cadre d’un cours de première année de classes préparatoires dans un lycée lyonnais. Le logiciel utilisé était Maple, et le but de ce TP était de réfléchir aux algorithmes et aux justifications mathématiques de ces algorithmes tout en faisant un petit voyage à travers l’histoire des mathématiques.

Première époque, le règne de la géométrie : la méthode d’Archimède

Le nombre π apparaît à l’origine comme la longueur du cercle de diamètre 1. La méthode d’Archimède de détermination de π consiste ‡ encadrer le cercles par deux polygones, l’un inscrit et l’autre exinscrit dont les longueurs encadrent la longueur du cercle puis d’augmenter le nombre de côtés des polygones. Sur ce dessin, on part des carrés dont les périmètres sont un premier encadrement de π : On double alors le nombre de côtés du polygone : Déterminer la formule de récurrence donnant le périmètre du polygone inscrit à 2n côtés connaissant le périmètre du polygone inscrit à n côtés. Même question pour le polygone exinscrit. Programmer avec Maple cet encadrement de π.

L’intérêt de cet algorithme est double : d’une part, il donne une approximation de π en s’appuyant sur des considérations géométriques élémentaires, toujours intéressantes à réactiver et d’autre part, il débouche sur une réflexion mathématique sur le lien existant entre la convergence des courbes et la convergence des longueurs des courbes. Le contre-exemple célèbre étant le « paradoxe » proposé par la construction suivante :

Soit [AB] un segment de longueur 1 ; on construit un triangle rectangle et isocèle en C₁ : AC₁B

On construit alors les milieux respectifs des segments [AC₁], [AB], [C₁B] (respectivement C₂, C₃ et C₄)

On poursuit le processus, et on obtient la ligne brisée :

La longueur de chacune de ces lignes vaut . Et comme la ligne brisée « converge » vers le segment [AB], on en déduit que =1 !

Deuxième époque, le triomphe de l’algèbre : la méthode de Viète

La méthode de Viète est la première méthode débouchant sur un produit infini. Elle consiste à mesurer l’aire d’un polygone à 2ⁿ côtés inscrit dans le cercle de rayon 1.

1. En utilisant des considérations géométriques élémentaires, démontrer que le rapport des aires des polygones à 2ⁿ⁺¹ côtés et à 2ⁿ côtés vaut .
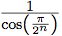2. En utilisant la formule 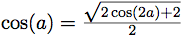en déduire que :

   

3. Programmez cette méthode avec Maple.

La suite récurrente permet une bonne illustration d’une procédure récursive.

Troisième époque, l’avènement de l’analyse :

la méthode de Wallis

Wallis publie en 1655 la formule de produit infini suivante :

Preuve :

On considère l’intégrale que l’on intègre en utilisant une intégration par parties :

et, en remplaçant sin² x par 1 - cos² x on trouve :

nW_n = (n - 1)W_{n - 2}

En exprimant W_2p en fonction de W₀ et W_2p+1 en fonction de W₁, on obtient :

Du fait que x appartient à l’intervalle et donc

On en déduit que tend vers 1 quand n tend vers +∞, puis la formule de Wallis.

1. Programmez la formule de Wallis
2. Comparez la vitesse de convergence avec les formules précédentes.

Un exemple classique de convergence dont la résolution passe par un calcul intégral et une double formule de récurrence suivant les indices pairs ou impairs est intéressante à étudier pour les techniques mises en place ; l’utilisation de la fonction « product » de Maple donne un résultat rapide ; il est possible ici encore de programmer récursivement la formule de Wallis.

La méthode de Newton

Il s’agit d’une généralisation de la formule du binôme en donnant à n des valeurs quelconques :

En remarquant, par ailleurs que la dérivée de arcsin est , on en déduit un développement de arcsin en somme infinie :

Et, en prenant , il vient :

1. Programmez la formule de Newton
2. Comparez la vitesse de convergence avec les formules précédentes

La encore, les techniques utilisées ont un caractère de modèle et pourront resservir à d’autres fins. Les commandes Maple permettent une programmation simple et une comparaison aisée avec les méthodes précédentes.

Quatrième époque, des statistiques aux probabilités

la méthode de Monte-Carlo

Algorithme :Choisir deux nombres au hasard entre 0 et 1.

Ces nombres sont les coordonnées d’un point du carré unité. La probabilité qu’il appartienne au quart de cercle est égal au rapport des aires du quart de disque et du carré unité soit .

1. Ecrire une procédure Maple simulant cette expérience aléatoire.
2. En déduire une valeur approchée de π.

L’aiguille de Buffon

Sur un parquet formé de planches de largeur 2a, séparées par des rainures droites, parallèles et équidistantes, on jette une aiguille de longueur 2l, avec l<a. Quelle est la probabilité que l’aiguille coupe l’une des rainures (événement A) ? Soit x la distance du milieu de l’aiguille à la rainure la plus proche. x prend une valeur aléatoire quelconque dans [0, a]. Soit θ l’angle des droites formées par cette rainure et l’aiguille. θ prend une valeur aléatoire quelconque dans [0,π]. Dans une représentation cartésienne du pavé Ω=[0, a]× [0,π], l’événement A est représenté par la partie hachurée délimitée par la courbe d’équation y = lsin(θ). Dans cette représentation, on prend pour modèle probabiliste la loi uniforme sur le rectangle Ω. La probabilité de A est donc le rapport de l’aire sous la courbe et du rectangle de longueur π et de hauteur a. On a donc

Ecrire une procédure Maple pour simuler l’expérience de l’aiguille de Buffon.

L’intrusion des probabilités dans ce paysage n’est certainement pas pour apporter une efficacité supplémentaire à la détermination des valeurs approchées de π, mais montre bien différentes approches d’un même problème. Par ailleurs, la méthode de Monte-Carlo pourra être réinvestie pour la résolution d’autres problèmes. L’aiguille de Buffon prend sa place dans cette étude du fait de son intérêt historique mais aussi des hypothèses probabilistes sous-jacentes qui pourront être reprises dans le problème plus paradoxal de Bertrand :

on choisit une corde au hasard dans un cercle. Quelle est la probabilité que la longueur de cette corde soit plus petite que le côté du triangle équilatéral inscrit ?

Dans ce problème, le choix du modèle probabiliste débouche sur des solutions différentes créant un « paradoxe ». La programmation de cette expérience montre bien la nécessité de choix qui se traduisent mathématiquement par des choix du modèle probabiliste utilisé ce qui permet de lever l’apparent paradoxe. Confère, par exemple http://sierra.univ-lyon1.fr/irem/an2000/web/paradoxe/paradoxe.html

Cinquième époque, la puissance des algorithmes au vingtième siècle

En 1973, Eugène Salamin et Richard Brent ont publié indépendamment un algorithmes fondé sur la moyenne arithmetico-géométrique dont la convergence est très rapide :

p_k est une approximation de π.

1. Programmez cet algorithme
2. Comparez la vitesse de convergence avec les formules précédentes.

Il était important dans ce TP de montrer en quoi la recherche d’approximations de π malgré son caractère désuet est encore d’actualité, notamment d’un point de vue algorithmique pour tester de nouveaux algorithmes dont l’usage peut s’avérer utile dans d’autres contextes.

Ce bref panorama ne prétend pas à l’exhaustivité mais montre bien le lien entre l’algorithmie, les mathématiques et l’histoire avec des étudiants ; l’usage de Maple a permis ce voyage rapide et les techniques utilisées peuvent sûrement être réinvesties dans d’autres contextes.