par Benjamin Clerc
Les auteurs de l’article : Benjamin Clerc, Hussein Sabra, Jacques Planes, Jacques Salles, Marie-Claire Combes, Marie-José Valéro, Nicolas Moreau, Patrick Imbert
1. Introduction et contexte général
Les TICE et leurs usages dans l’enseignement des mathématiques ont fait l’objet de recherches en didactique des mathématiques dès le début des années 90. Durant ces dernières années, les problématiques de recherche ont évolué, en parallèle avec l’évolution des technologies (Sabra et Trouche 2009). Nous sommes passés d’un questionnement sur la complexité d’intégration des TICE dans les classes de mathématiques à un questionnement sur les ressources mathématiques permettant de soutenir l’intégration de ces outils dans les classes. Les enjeux actuels de la recherche sont en rapport étroit avec le développement du numérique et des réseaux (le Web 2.0) offrant une opportunité d’articulations entre différentes applications.
L’ensemble de ces évolutions suscite en retour de nouveaux besoins et rend plus complexe le travail des enseignants. Un professeur dispose d’un ensemble de ressources variées : sites web, logiciels, mais aussi manuels papiers et productions d’élèves… Cet accès aux ressources, qui a lieu principalement en dehors de la classe, est central pour la préparation de son enseignement. Un simple recours à des ressources, pourtant abondantes sur de nombreux sites, ou un simple échange de ressources ne suffit bien sûr pas à prendre en charge cette complexité. L’ensemble de ces facteurs a favorisé, en s’appuyant sur le Web 2.0, l’émergence de nouvelles formes de travail collectif entre les enseignants de mathématiques. Le travail de sélection, d’adaptation, de modification, de combinaison et de création des différents scénarios didactiques pour la mise en œuvre en classe constitue ce que l’on appelle le travail documentaire des enseignants (Gueudet et Trouche 2010).
Les plateformes en ligne ayant des enjeux d’apprentissage didactique et mathématique sont de différents types :
- plateformes contenant des ressources à destination des élèves ;
- plateformes contenant des ressources à destination des enseignants, pour préparer leur enseignement (des ressources libres et gratuites, modifiables et adaptables, avec différents scénarios d’usages) ;
- plateformes contenant des ressources pour la formation des enseignants (en autonomie, ou accompagné à distance).
A l’instar de Artigue et Gueudet (2008), nous considérons les plateformes en ligne comme des méta-structures qui aident les enseignants à faire face au foisonnement des ressources en ligne, en ne laissant pas à leur seule charge la sélection des ressources de qualité, en donnant des moyens pour capitaliser les avancées et surmonter l’éclatement. De telles méta-structures sont certainement nécessaires. En revanche, il nous semble que l’articulation entre conception et usage reste une tâche à accomplir, notamment dans le cas ou les interactions entre concepteurs et usagers sont absentes. L’éventail de plateformes offertes nous pousse à nous poser des questions sur les rapports entre conception, usage et formation de façon productive. La formation ici est entendue dans le sens d’une piste potentielle pour assurer une certaine passerelle entre concepteurs et usagers. Une ressource en ligne doit pouvoir évoluer, pour intégrer les apports des utilisateurs et, en un sens, tout utilisateur doit également être considéré comme un concepteur potentiel. On passe ainsi d’une tradition de ressources conçues pour les enseignants à des ressources conçues avec ceux-ci, selon le principe de conception dans l’usage (Rabardel et Bourmaud 2005).
Adopter cette perspective signifie réfléchir à la question : Comment la considération des ressources en lignes constitue un support pour construire un rapport entre conception et usage ? Quels effets éventuels sur l’évolution de la ressource ? Nous allons traiter cette question à partir d’une étude de cas, en considérant pour la même ressource deux types d’usagers : enseignants de mathématiques et formateurs. Pour l’étude de ce questionnement, nous présentons une étude de cas : ressource mathématique développée dans le cadre d’un projet européen (§ 2). Après la présentation du processus de conception de la ressource, nous en présentons différents types d’usage : dans le cadre d’un parcours de formation continue (§ 3), comme dans le cadre d’enseignement en classes (§ 4). Nous terminons par une conclusion en rapport avec le questionnement (§ 5).
2. Le compas dans l’œil, ressource de la plateforme EdUmatics
2.1 EdUmatics
2.1 EdUmatics projet européen, conception d’une plateforme mathématique en ligne
Le projet EdUmatics (European development for the Use of mathematics technology in the classrooms, 2009-2012) s’est donné pour objectif de mettre à disposition des enseignants de mathématiques européens [1] du secondaire différents types de ressources permettant d’assister l’intégration des technologies dans leur enseignement des mathématiques. Les ressources proposées incitent à une réflexion sur des situations mathématiques et sur la pertinence de certains choix didactiques justifiant l’utilisation des logiciels mathématiques dans ces situations. Cinq modules sont offerts sur la plateforme en ligne (www.edumatics.eu) diversifiée du point de vue de l’usage des TICE :
- Commencer le travail avec les TICE ;
- Des représentations statiques aux représentations dynamiques, où sont présentées des pistes d’usages des représentations dynamiques qu’offrent les logiciels au profit de la compréhension de certains concepts mathématiques ;
- Modéliser avec des fonctions ;
- Utiliser les technologies en classe, où l’on incite à une réflexion sur les usages effectifs des TICE dans les classes de mathématiques à partir de certaines situations et extraits vidéos ;
- Usage inter-relié de logiciels mathématiques, où l’on apprend à évaluer la pertinence de l’utilisation de telle ou telle représentation pour la recherche d’un problème et leur apport respectif à cette recherche ; l’exploitation des inter-relations entre ces représentations (géométrique, numérique, graphique, et formelle) est bénéfique pour l’apprentissage des mathématiques. Le groupe IREM « Intégration des Outils Informatiques » à Montpellier a été amené à concevoir et expérimenter des ressources pour ce dernier module.
Le module 5 contient des ressources à destination des enseignants sous une présentation progressive. A un premier niveau se situent des ressources visant à familiariser les enseignants avec une seule représentation. L’objectif de ce premier niveau est de fournir aux enseignants des problèmes mathématiques à destination d’élèves conçus de telle sorte qu’une représentation particulière facilite de façon pertinente l’émergence de conjectures. Au deuxième niveau se situent des ressources qui ont pour but d’introduire progressivement deux représentations qui enrichissent sous plusieurs angles le traitement du problème mathématique posé. L’interaction entre plusieurs représentations, au cœur du module 5, est l’objectif essentiel du dernier niveau de ressources. « Le compas dans l’œil » est une de ces ressources.
2.2 Une situation mathématique
2.2 Une situation mathématique : le compas dans l’œil
La situation mathématique « le compas dans l’œil » (voir Encadré 1). Le problème proposé dans cette situation concerne la comparaison de séries statistiques et s’intéresse à la recherche de critères pertinents pour effectuer ce traitement. La richesse de cette situation provient du fait qu’il n’y a pas de solution a priori. La solution dégagée est étroitement liée aux critères fixés par les joueurs.
| la situation mathématique « compas dans l’œil » La situation proposée permet de tester votre capacité à placer au mieux un point qui finalise diverses configurations géométriques particulières telles que milieu d’un segment, parallélogramme, bissectrice, point de convergence de trois rayons lumineux ... Chaque jeu consiste à réaliser trois séries de sept configurations. Le tableau situé sur la partie droite de l’écran de jeu affiche pour chaque question de chaque série l’erreur (mesurée en pixels ou degrés suivant les différentes questions) entre votre choix et la réponse théorique ; il affiche aussi l’erreur moyenne et le temps total réalisé. a) Réalisez trois jeux (c’est-à-dire trois fois trois séries de sept configurations) et observez dans le diagramme en barres affiché votre positionnement par rapport aux 10000 derniers joueurs. b) Quel est le meilleur de vos trois jeux ? Explicitez les critères de choix de votre réponse. |
Encadré 1. La situation mathématique « compas dans l’œil »
La situation mathématique, telle qu’elle est proposée, amène les élèves à utiliser une application externe [2]. Un temps d’appropriation de cette application est donc nécessaire pour trois raisons :
- l’application étant conçue en langue anglaise, certains termes techniques peuvent ne pas être familiers aux élèves dont ce n’est pas la langue maternelle ;
- un apprentissage du logiciel est inévitable ; la stratégie naturelle d’essais et erreurs sera certainement privilégiée par les élèves ;
- les questions mathématiques posées se rapportent au domaine de la géométrie. La réponse à ces questions demande de la part des élèves une mobilisation de connaissances géométriques antérieures (niveau collège).
Dans leur choix de désignation du meilleur jeu, on peut s’attendre à voir les élèves privilégier l’un des trois critères :
- le meilleur jeu est celui qui a été réalisé dans le temps minimum ;
- le meilleur jeu est celui qui affiche une erreur moyenne minimale ; on notera que ce choix peut être influencé par l’apparition à l’écran des 500 meilleurs scores ;
- le meilleur jeu est celui qui a le « meilleur couple » (temps, erreur moyenne). Mais un tel choix nécessite une définition du terme « meilleur couple ». La définition de « meilleur couple » adoptée par les joueurs détermine la corrélation des deux variables (temps, erreur moyenne). Une harmonisation des propositions de définitions par les élèves est inévitable et ne peut avoir lieu que par la mise en place d’un débat dans la classe.
Le caractère ouvert du processus de résolution rend cruciale la question de scénarisation de la mise en œuvre.
2.3 Implémentation
2.3 Implémentation de « compas dans l’œil » dans la plateforme EdUmatics
La situation est susceptible d’être soumise à des élèves. Son expérimentation dans la classe constitue une étape incontournable du processus de son appropriation par un enseignant. L’expérimentation va pousser l’enseignant à mener une réflexion didactique sur la situation.

Figure 1. L’aperçu de la ressource « compas dans l’œil » dans la plateforme EdUmatics.
Le processus d’implémentation de la ressource dans la plateforme Edumatics passe, comme toutes les ressources, par une analyse a priori développée au sein de notre équipe IREM. Dans cette analyse a priori nous sommes amenés à nous interroger sur les stratégies susceptibles d’être utilisées par les élèves pour résoudre le problème et à réfléchir à l’environnement technologique adéquat en listant les avantages et inconvénients des différentes représentations proposées. A l’issue de ce travail, deux questions sont posées aux enseignants usagers de la ressource mise à disposition sur la plateforme (Annexe 2). Des éléments de réponse aux questions posées sont mis à la disposition des enseignants.
3. Compas dans l’œil, usage dans le cadre de la formation continue
La ressource a été utilisée en formation de professeurs de mathématiques dans le cadre du PAF [3] dans l’Académie de Montpellier, ce stage avait pour intitulé « Intégrer l’utilisation d’un ENT dans la classe de mathématiques », elle a été l’occasion de montrer comment intégrer une ressource dans l’ENT de l’Académie de Montpellier et dans labomep.
3.1 Intégration dans l’ENT académique
3.1 Intégration de la ressource dans l’ENT académique
Il y a plusieurs types d’intégration de la ressource dans l’ENT académique :
- déposer la ressource sous la forme d’un fichier texte mis à disposition des élèves ou des stagiaires au téléchargement depuis l’espace de stockage.
- envoyer la ressource aux élèves ou aux stagiaires concernés, sous la forme d’un fichier texte attaché via la messagerie interne de l’ENT.
- intégrer la ressource dans un cours.
Ce dernier choix a été retenu car il permet d’illustrer des potentialités de la plateforme et de faciliter l’appropriation d’une ressource mathématique. Dans l’ENT académique, il est possible de créer des cours en utilisant Moodle [4]], permettant non seulement la visualisation de la ressource mais également la collecte des travaux ou réponses des élèves ou des stagiaires.
Nous avons donc créé un cours portant le nom du stage, ce travail a été fait par deux des formateurs, il est en effet possible d’être plusieurs rédacteurs d’un même cours dans Moodle, intervenant sur des parties séparées ou communes du cours. Les co-rédacteurs peuvent être d’établissements différents, c’est notre cas.

Figure 2. La page d’accueil de Moodle
La ressource élève (Annexe 1) peut être intégrée au cours en plein texte ou proposée au téléchargement, il est possible de collecter les résultats dans l’ENT.
- à l’intérieur d’un cours Moodle via un sondage ;
- à l’intérieur d’un cours Moodle via un espace de dépôt de documents ;
- en utilisant la messagerie interne, charge au professeur de réaliser ensuite le fichier de collecte ;
- en utilisant un forum dédié à cela, les élèves peuvent alors être chargés de réaliser eux-mêmes ce fichier de collecte ;
- en utilisant l’espace de dépôt de fichiers, charge au professeur de réaliser ensuite le fichier de collecte.
Sur le site Edumatics les propositions de réponse à destination des professeurs sont cachées et peuvent apparaître dans le texte en cliquant sur un lien, cette fonctionnalité ne peut pas être proposée dans un cours Moodle, les propositions de réponse ont donc été créées dans le cours Moodle sous forme de pages html accessibles en suivant un lien.
3.2 Intégration dans Labomep
3.2 Intégration de la ressource dans Labomep
La ressource a également été intégrée dans Labomep. Labomep est une plateforme mathématique qui permet aux professeurs de donner du travail à leurs élèves en proposant des ressources mathématiques variées. Une fois inscrits, les élèves se connectent (à l’adresse www.labomep.net), font les exercices programmés par le professeur et leur travail est enregistré ; le professeur peut alors consulter les résultats de ses élèves. Chaque enseignant utilisateur de Labomep peut concevoir et déposer ses propres ressources.
La ressource créée à l’intention des élèves comporte une consigne qui contient la traduction du mode d’emploi du jeu, celui-ci étant en langue anglaise, et qui demande aux élèves d’utiliser la zone « Réponse » pour renseigner les résultats obtenus lors de leurs trois tentatives. Dans le bilan de la séance, le professeur a alors accès à l’ensemble des réponses données par ses élèves, il peut alors réaliser le fichier de collecte rapidement (voir figure 3).

Figure 3. L’aperçu, pour l’élève, de la ressource « le compas dans l’œil »
Dans Labomep il est possible de créer une classe dans laquelle tous les stagiaires sont inscrits ou encore d’utiliser une classe avec des comptes fictifs et donc de mettre les stagiaires dans la position d’un élève pour utiliser la ressource professeur. Le même problème ergonomique présent dans Moodle est rencontré dans Labomep (§ 3.1), il peut être contourné en créant trois ressources au lieu d’une : une ressource principale (voir figure 4) ; deux annexes (voir figure 5) ; et des liens entre ces annexes et la ressource principale.

Figure 4. La ressource professeur « le compas dans l’œil », implémentée dans Labomep

Figure 5. Les propositions de réponses aux questions posées à l’enseignant en formation
3.3 Scénario
3.3 Scénario pour la mise en place de la formation
Le stage avait lieu à l’IREM de Montpellier, il est à destination des professeurs de mathématiques en collège et lycée, le contenu de la formation était le suivant :
- Utiliser de manière pertinente des logiciels sur LoRdi (Ordinateur portable dont sont dotés tous les élèves de lycée de l’Académie de Montpellier) ;
- Communiquer avec les élèves via l’ENT de l’Académie de Montpellier ;
- Intégrer l’usage des TICE avec les élèves dans et en dehors de la classe.
En introduction, les différents types de plateformes utilisées dans la formation sont présentés :
- l’ENT de l’Académie de Montpellier et la possibilité de mettre en ligne du contenu via Moodle ;
- Labomep, l’ENT mathématiques, libre et gratuit, développé par Sésamath, et la possibilité de proposer des séances d’exercices incluant ses propres productions ;
- Edumatics, une plateforme d’e-learning européenne, permettant aux enseignants de s’auto-former à l’utilisation des TICE dans l’enseignement des mathématiques.
La ressource « compas dans l’œil » est présentée aux stagiaires dans la plateforme Edumatics, ce qui permet de mettre en évidence les différents cours, ressources pour les professeurs et ressources pour la classe qui se trouvent sur cette plateforme.
Une phase de manipulation et de recherche individuelle du problème est proposée aux stagiaires. Une discussion collective est engagée autour du meilleur score, il y a un choix qui a été fait sur le site (en fonction du nombre minimal des pixels), mais que faire du temps ? Si celui-ci est pris en compte, la question qui se pose est « Quel est le meilleur couple (erreurs, temps) ? ». Or on ne peut pas parler d’un meilleur couple dans ce cas, car il y a une superposition de deux espaces vectoriels et pas un seul espace vectoriel avec une base et une dimension.
Deux exemples d’implémentation de la ressource « compas dans l’œil » sur l’ENT et Labomep sont alors proposés aux stagiaires, ce qui suppose une adaptation de la ressource en fonction des potentialités offertes par les plateformes :
- interactions avec les élèves (en présence, à distance) ;
- modalités de recueil des données statistiques des élèves ;
- interface de la plateforme dont sa maîtrise est en rapport avec les compétences d’utilisation des outils informatiques de l’enseignant.
L’usage de la ressource dans le cadre de la formation est déterminé par la méta-structure (plateforme) qu’elle porte. Les potentialités de la plateforme déterminent la configuration de la mise en œuvre en classe de la ressource.
4. Compas dans l’œil, différentes adaptations possibles pour les classes de mathématiques
La ressource compas dans l’œil est expérimentée dans 5 classes de différents niveaux d’enseignement : collège (en troisième), lycée (seconde et première scientifique). L’analyse de ces expérimentations a fait émerger deux questions possibles : 1) quel est le meilleur jeu ? ; 2) Quel est le meilleur joueur ? En fonction de ces deux questions, trois configurations sont possibles engendrant chacun un ou plusieurs scénarios :
- une première configuration où on pose la question du meilleur jeu seulement ;
- une deuxième configuration où on pose la question du meilleur joueur seulement ;
- une troisième configuration où on pose la question du meilleur jeu et celle du meilleur joueur successivement.
Nous présentons dans ce qui suit chacun des cas en fonctions de (des) scénarios associé(s) qui ont eu lieu dans nos expérimentations.
4.1 Une première configuration
4.1 Une première configuration : la question du meilleur jeu
Dans cette première configuration, nous avons expérimenté deux scénarios :
a) Scénario avec débat ouvert
Nous avons expérimenté la ressource dans deux classes de niveaux différents (3e et 2nde ) en suivant le même scénario. Pour ces deux classes, les enseignants disposent d’une heure dédoublée, ce qui leur permet de faire des travaux en demi-classe et ont ainsi la possibilité de travailler en groupe. Cette configuration permet donc d’initier les élèves aux travaux de recherche en mathématiques.
Cette ressource a donc été expérimentée à deux reprises avec deux demi-classes d’une quinzaine d’élèves environ à chaque fois. Des groupes de 3 ou 4 élèves avaient constitué au préalable. L’expérimentation s’est déroulée en salle informatique où chaque élève avait un ordinateur à sa disposition. Cette séance faisait suite à la leçon « Statistiques » et « Notion de fonction » pour les 3e et les notions du programme de 2nde avaient été presque toutes vues à ce moment de l’année. En particulier les statistiques avaient été traitées au premier trimestre.
Les élèves avaient tous eu l’occasion de faire des activités en salle informatique où ils étaient amenés à utiliser le tableur.
Le scénario choisi avait pour objectif d’amener les élèves à réfléchir aux choix des critères permettant de définir le meilleur jeu sous forme de débat collectif. Lorsqu’un élève réalise seul ses trois jeux, le logiciel affiche un score comprenant deux données : le temps et l’erreur moyenne. Il peut également se positionner dans un classement établi par les utilisateurs précédent du jeu. A l’issue de chaque jeu, l’élève souhaitant améliorer sa performance doit faire un choix stratégique : aller plus vite au détriment de la précision ou être plus précis en prenant son temps ? Le choix est donc individuel. Mais est-ce la bonne solution ?
Afin d’apporter des éléments de réponses à leurs choix individuels, nous proposons aux élèves de travailler d’abord en petits groupes afin de réfléchir et d’échanger sur leur propre choix et de faire émerger des critères sur la meilleure façon de jouer. Ensuite, nous proposons aux élèves de présenter leurs idées et d’en débattre. L’objectif de cette phase collective de débat est d’apprendre à argumenter, communiquer et présenter une démarche scientifique oralement. L’utilisation d’un langage mathématique approprié nous paraît importante pour débattre efficacement en classe. Ce type d’activité conforte l’élève dans la nécessité d’un langage clair et précis lors de l’explication de son raisonnement.
Effectuant cette expérimentation en demi-classe, nous avons pensé qu’il était possible de réaliser ce scenario en une séance d’une heure. Mais cela nécessite une bonne gestion.
La séance s’est donc déroulée en trois étapes :
- la 1ère étape est individuelle : les élèves réalisent trois jeux à partir d’un site internet. Après une phase d’appropriation du jeu, les élèves ont vite compris les règles et se sont montrés désireux d’améliorer leur score. Différentes stratégies se sont mises en place afin d’améliorer leur jeu : rapidité, précision …. mais est-ce là bonne ?
- dans une 2ème étape, afin de réfléchir à cette problématique, nous proposons, aux élèves de se rassembler en petits groupes de 3 ou 4 afin de répondre à la question : « Quel est le meilleur de vos trois jeux ? Explicitez les critères de choix de votre réponse. ». Les élèves ont pour consigne de travailler ensemble dans chaque groupe afin de participer à l’argumentation de tous les choix. Ils ont ainsi l’occasion d’échanger sur leur propre stratégie. Le travail en petits groupes permet un premier débat où différents critères émergent. Les enseignants doivent exiger des traces écrites des élèves et animer les différentes discussions des groupes, tout en relançant la problématique. Chaque groupe arrive ainsi à faire émerger des critères prépondérants à ses ses yeux sur le meilleur jeu ;
- dans une 3ème étape, après avoir observé les différentes propositions de chaque groupe, les enseignants proposent alors à chacun de présenter ses idées et d’en débattre dans la classe. Cette phase permet ainsi de comparer les résultats tout en explicitant oralement les critères. Au cours du débat, les élèves ont la possibilité de vérifier de nouvelles hypothèses évoquées entre eux, en utilisant éventuellement les ordinateurs pour créer des tableaux, graphiques ou autre.
Certains groupes de 3ème jugent, tout d’abord, que le meilleur des trois jeux est le dernier. Mais suite aux débats, il apparaît que le choix de critères différents permet de conclure que le meilleur n’est pas forcément le dernier. (moyenne simple, moyenne pondérée, etc ….
En 2nde, des groupes ont choisi de traiter le problème à l’aide de graphique et en particulier les distances entre l’origine du repère et les points de coordonnées (score ;temps). Des élèves sont même allés plus loin dans leur raisonnement et ont abordé le changement d’échelles. (Voir partie 4.4 Analyse des productions des élèves)
Pour ces deux classes de niveaux différents (3e et 2nde), le scénario suit la même trame mais il peut être adapté en fonction des classes et des attentes de l’enseignant. Les outils utilisés par les élèves sont différents, l’enseignant dispose ainsi d’une certaine flexibilité en fonction des usages et des pratiques des élèves.
Ce scénario possède cependant quelques limites d’utilisation. Les propositions pour définir les critères du meilleur jeu apportées pas les élèves peuvent ne pas être toujours pertinentes, l’enseignant peut alors éprouver quelques difficultés à motiver les élèves dans une démarche de recherche plus approfondie (par exemple, « plus je m’entraine plus je m’améliore ! »). Une séance d’une heure est peut-être un peu courte pour arriver à développer exploiter les différentes traces de recherche des élèves. A la fin du débat, certains élèves de 3e ont proposé de nouvelles pistes de recherche, avec tracé de graphique et possibilité d’utiliser un tableur, mais le manque de temps n’a pas permis de finaliser cette idée. Les réponses des élèves et le débat qui s’ensuit peuvent être totalement différents d’un groupe à l’autre, et l’exploitation du résultat peut donc s’avérer assez délicat à l’issue de ces séances. L’enseignant devra alors rajouter une étape supplémentaire en classe entière afin de synthétiser l’ensemble et éventuellement approfondir le débat.
b) Scénario avec débat guidé par l’enseignant
Ce deuxième scénario s’est déroulé dans une classe de première scientifique constituée de 35 élèves d’un niveau considéré moyen. La séance s’est déroulée dans une classe où chaque élève dispose de son ordinateur. La salle est équipée d’un vidéo projecteur relié à un poste professeur. Le lien vers la ressource en ligne est inscrit dans l’espace réservé à la classe dans l’ENT académique. Un fichier tableur est aussi déposé au même endroit. L’expérimentation a eu lieu lors d’une séance de 2 heures au cours du deuxième trimestre et précision importante, après avoir fait le cours sur les statistiques.
Ce scénario et son expérimentation se sont déroulés en plusieurs étapes :
- première étape d’expérimentation individuelle : Les élèves doivent réaliser trois séries consécutives et noter les temps et scores obtenus. Ils ont ensuite à inscrire leurs résultats, via l’ENT, dans la feuille de calcul préparée à cet effet ;
- deuxième étape de débat collectif guidé et géré par l’enseignant. Durant cette étape, l’enseignant pose la question : « Quel est le meilleur de vos trois jeux ? » et demande aux élèves de réfléchir à la justification de la réponse qu’ils vont donner. Ensuite sur le tableau blanc, les élèves, à tour de rôle, vont inscrire leurs justifications si elles sont différentes de celles déjà écrites ou cocher celle qu’ils ont choisie.
- troisième étape, suite du débat guidé par l’enseignant et utilisation du vidéoprojecteur. L’enseignant pose la question : « Comment déterminer à partir du tableur le meilleur jeu réalisé ? » et demande aux élèves de réfléchir en groupe, puis de proposer une méthode.
Après un temps de recherche, mise en commun des résultats, deux écoles s’affronteraient : les calculateurs et les graphistes. Les premiers proposent toutes sortes de calculs allant de la somme pure et simple à la moyenne des temps et scores (statistiques faites un peu avant !). Les différentes solutions proposées et projetées sont rapidement mises en défaut. Les seconds (statistiques toujours) proposent de manière quasi unanime de faire un nuage de points (nuage assez conséquent : une centaine de points).
4.2 La deuxième configuration
4.2 La deuxième configuration : la question du meilleur joueur
Ce scénario se place dans le cadre du cours de mathématiques d’une classe de 2nde de niveau hétérogène. Les notions qui devraient être traitées en classe à ce stade de l’année étaient : statistiques descriptives, généralités sur les fonctions, coordonnées et distance entre deux points. Nous visons un scénario qui permet aux élèves de :
- être confrontés à une situation inattendue et originale, en espérant intéresser chacun d’entre eux, et en particulier ceux qui commencent à décrocher un peu à ce stade de l’année,
- être amené à établir une stratégie : comment procéder, quelle démarche suivre, quel raisonnement mener pour passer des valeurs affichées au tableau au choix du meilleur joueur ?
- être amené à choisir des critères : il y a le temps qui doit être le plus petit possible et le score donnant la précision qui doit être aussi le plus petit possible, mais le fait de réduire l’un provoque en général l’augmentation de l’autre. Comment combiner les deux ?
- s’exprimer dans un débat de type scientifique,
- mettre du sens dans les calculs : quand il faudra combiner les deux valeurs qui ne sont ni dans la même unité ni du même ordre de grandeur, par exemple dans une somme.
La séance dure 2h (mais en fait 1h30 effective) et se déroule classe entière. La salle, avec ses 18 ordinateurs au fond, permet de partager la classe en deux : ceux qui sont sur les ordinateurs et ceux qui travaillent « sur table ». Cette configuration est intéressante car les élèves ont toujours les ordinateurs à disposition et peuvent choisir ou pas de l’utiliser comme outil de travail. Ce n’est pas le cas quand un enseignant réserve une salle informatique : les élèves savent qu’il y a un travail à faire sur les ordinateurs, et n’ont pas le choix de l’outil. La salle est également équipée d’un vidéo projecteur.
Le travail s’organise en quatre parties. Une première partie de présentation au vidéo projecteur, en tout début de séance, de la procédure pratique pour aller sur le site du jeu, ainsi que du jeu lui-même avec sa particularité d’être en anglais. Une deuxième partie où les élèves, séparés en deux demi-classes, vont sur les ordinateurs du fond de la salle, à tour de rôle. Ils ont pour consigne :
i. faire un jeu d’essai, dans un objectif d’appropriation de l’interface et de la nature du jeu ;
ii. faire un jeu complet, avec ses trois séries ;
iii. ramener le temps et le score quand ils ont fini. Ces données sont inscrites au fur et à mesure dans un fichier de type tableur prévu à cet effet.
Pendant qu’un groupe passe sur les ordinateurs, nous faisons avec l’autre groupe le bilan d’une activité sur les trinômes faite la veille en TP. Ces deux premières parties prennent une heure.
Au cours de la 2ème heure de la séance, les élèves doivent désigner le meilleur joueur de la classe, au vu de tous les résultats affichés au tableau à l’aide du vidéo projecteur. Là encore le travail se fait en deux temps. La troisième partie où le travail se fait par groupes d’élèves, pendant 15 minutes. Ils doivent noter toutes les idées qu’ils ont pour pouvoir désigner le meilleur joueur. Nous avions prévu 10 minutes, mais les élèves de certains groupes ont demandé un peu plus de temps pour approfondir et préciser leur démarche. Le travail de l’enseignant à ce stade, est d’aider les élèves bloqués à démarrer. La quatrième partie est celle du retour au groupe « classe entière ». Chaque groupe dicte l’idée qu’il a eue (souvent une seule car ils ont fait des essais avec leur calculatrice pour tester leur idée). Cette idée est notée au tableau, parfois exécutée directement à l’aide du tableur, quand il s’agit de calcul. Les effets sont alors directement et immédiatement (c’est un aspect dynamisant) visibles par tous.
Le débat scientifique s’installe alors dans la classe et chaque idée proposée peut être explicitée, et soumise à une critique.
Par contre, nous avons étés confrontés encore à un rejet de la part de certains élèves, et pour cela, il a fallu prendre le temps de trouver des exemples, inspirés de la vie, où l’on est obligé de composer avec des quantités qui ne sont pas du même ordre (compétition de slalom à ski, parcours de saut d’obstacles à cheval…), et cela a permis de raccrocher une partie de ces élèves.
Nous n’avons, dans l’idée de laisser les élèves s’exprimer, les invitant souvent à expliciter leur idée, pas pris assez de temps pour le point 4 des objectifs : mettre du sens dans les calculs.
Nous pensons qu’un travail hors temps scolaire pourrait être donné à l’issue de cette séance pour permettre de prendre du recul et fixer certaines idées abordées, et, pourquoi pas, en explorer d’autres.
4.3 La troisième configuration
4.3 La troisième configuration : question du meilleur jeu et meilleur joueur successivement
Le scénario présenté a été proposée à une classe de 3ème d’un bon niveau scolaire ; la partie statistique du programme de 3ème venait d’être étudiée en classe.
La séance est de 2 heures et se déroule classe entière en salle informatique. En périphérie de la salle, on dispose de 15 postes informatiques dont un relié à un vidéo projecteur et des tables de travail au centre de la pièce, ce qui permet de rester au même endroit lors de la mise en commun des réflexions des élèves ou des groupes d’élèves. Les élèves travaillent régulièrement dans cette salle et n’ont donc pas à se familiariser avec le matériel informatique.
Une semaine avant le déroulement de l’activité, une présentation en a été faite en classe à l’aide d’une vidéo projection afin d’expliciter les situations proposées et le mode de déroulement du jeu. Il était nécessaire que le côté vocabulaire géométrique en anglais et manipulation des objets géométriques aient été travaillés à l’avance par les élèves afin d’éviter un démarrage trop chaotique. Un lien a été donné aux élèves via le cahier de textes en ligne afin qu’ils puissent, sans obligation de faire, se familiariser avec le jeu à la maison.
Le scénario prévu devait amener les élèves à essayer d’élaborer des critères pertinents pour déterminer le meilleur jeu à titre individuel puis le meilleur jeu au sein du groupe de travail ; dans un deuxième temps, il s’agissait d’envisager comment déterminer le meilleur joueur au sein du groupe. Il est bien entendu qu’une question sous jacente était bien présente : comment, à titre personnel, améliorer son résultat : agir sur la précision sans tenir compte du temps ou agir sur le temps au détriment de la précision ? Le scénario est construit de la façon suivante :
- dans un premier temps (environ 30 minutes) les élèves travaillent individuellement. Ils sont deux par poste informatique et chacun d’eux va réaliser 3 jeux consécutifs et noter pour chaque jeu l’erreur moyenne et le temps mis pour le réaliser. Ils vont aussi noter chaque fois leur position sur le graphique des 10 000 derniers résultats. Dès qu’un élève a réalisé ses 3 jeux, il va les enregistrer dans une feuille de calcul de tableur ouvert sur le poste professeur de la salle informatique.
- dans un deuxième temps (environ 1 heure), la classe est divisée en 6 groupes ; chaque groupe se retrouve autour d’une table pour mettre en commun les résultats et les réflexions de ses membres afin de tenter de définir des critères judicieux afin de répondre aux deux questions suivantes :
1) Pour chacun d’entre vous, quel est votre meilleur jeu ? ;
2) Dans le groupe, quel vous semble être le meilleur joueur ? - la dernière période de la séquence (environ 15 minutes) a été consacrée à une brève synthèse faite par un élève de chaque groupe pour exposer à la classe les propositions de son groupe.
Un prolongement a été proposé à l’ensemble de la classe : après avoir récupéré le fichier tableur mis à leur disposition dans leur répertoire personnel et complété en début d’heure, il a été demandé aux élèves d’essayer de concrétiser les diverses propositions au niveau de la classe entière et ce travail donnera lieu à une exploitation ultérieure en classe.
Pour la première question, la réponse a été unanime : les élèves considèrent que le meilleur jeu est celui qui correspond à l’erreur moyenne la plus faible, sans tenir compte du temps mis pour l’effectuer. Ceci est en accord avec la représentation graphique donnée sur le site en fin de partie. Pour la deuxième question, un véritable débat s’est instauré au sein de chaque groupe et les propositions ont été multiples et variées. Les propositions faites sont dans ce cas plus ou moins pertinentes mais tentent toutes de réaliser de façon plus ou moins maladroite un équilibre « quantitatif » entre les deux critères pris en compte : la précision et la durée du jeu. Un groupe a tenté une approche graphique mais n’a pas pu l’exploiter de façon satisfaisante par manque d’un bagage suffisant dans ce domaine en 3ème.
L’essentiel de la séance a été de créer un vrai débat au sein de la classe autour d’un problème ouvert pour lequel personne ne détenait « la » réponse et pour lequel il fallait « inventer » une « règle du jeu » consensuelle et argumentée.
4.4 Analyse
4.4 Analyse des productions des élèves
Nous listons les critères fixés par les élèves. Nous illustrons ces critères par des extraits des productions d’élèves.
Dans ce cadre, nous présentons trois types de critères.
1er type de critères : la meilleure précision
A la question posée : « Quel est votre meilleur jeu ? », les élèves ont répondu de manière différente en fonction de leur niveau. Les élèves de troisième ont presque unanimement donné comme critère prépondérant la précision, il est vrai fortement influencés par la représentation graphique produite par le site en fin de partie.

Les autres ont placé la précision comme critère numéro 1 de classement mais ont aussi constaté que le temps devait intervenir.
Le troisième essai semble réunir une majorité de suffrages, ce qui tendrait à prouver la prépondérance de la précision, mais comment classer alors les joueurs entre eux ?
2ème type de critères : la présence de deux minimums
Pour répondre à la deuxième question, il a été rapidement convenu par la plupart des élèves qu’il fallait tenir compte des trois essais, mais dans un nombre non négligeable de jeux, il s’est avéré que les deux minima coïncidaient lors du troisième jeu.

Lors d’une expérimentation ; un groupe s’est même trouvé composé d’élèves ayant tous meilleur temps et score lors du troisième essai. L’enseignant a donc dispatché ce groupe en associant ses participants avec d’autres groupes.

Dans une autre expérimentation, le temps a été exclu pour répondre à la première question.
L’enseignant est donc passé à la question du meilleur joueur et, le fait que l’on doive tenir compte des trois jeux étant acquis, différentes stratégies se sont mises en place : calcul des moyennes, formule de calcul faisant intervenir les deux paramètres, coefficient affecté à la précision pour ramener les nombres dans une même échelle.
3ème type de critères : un mixte des deux grandeurs (pixels et temps)
Ce type de critère se décline sous plusieurs critères :
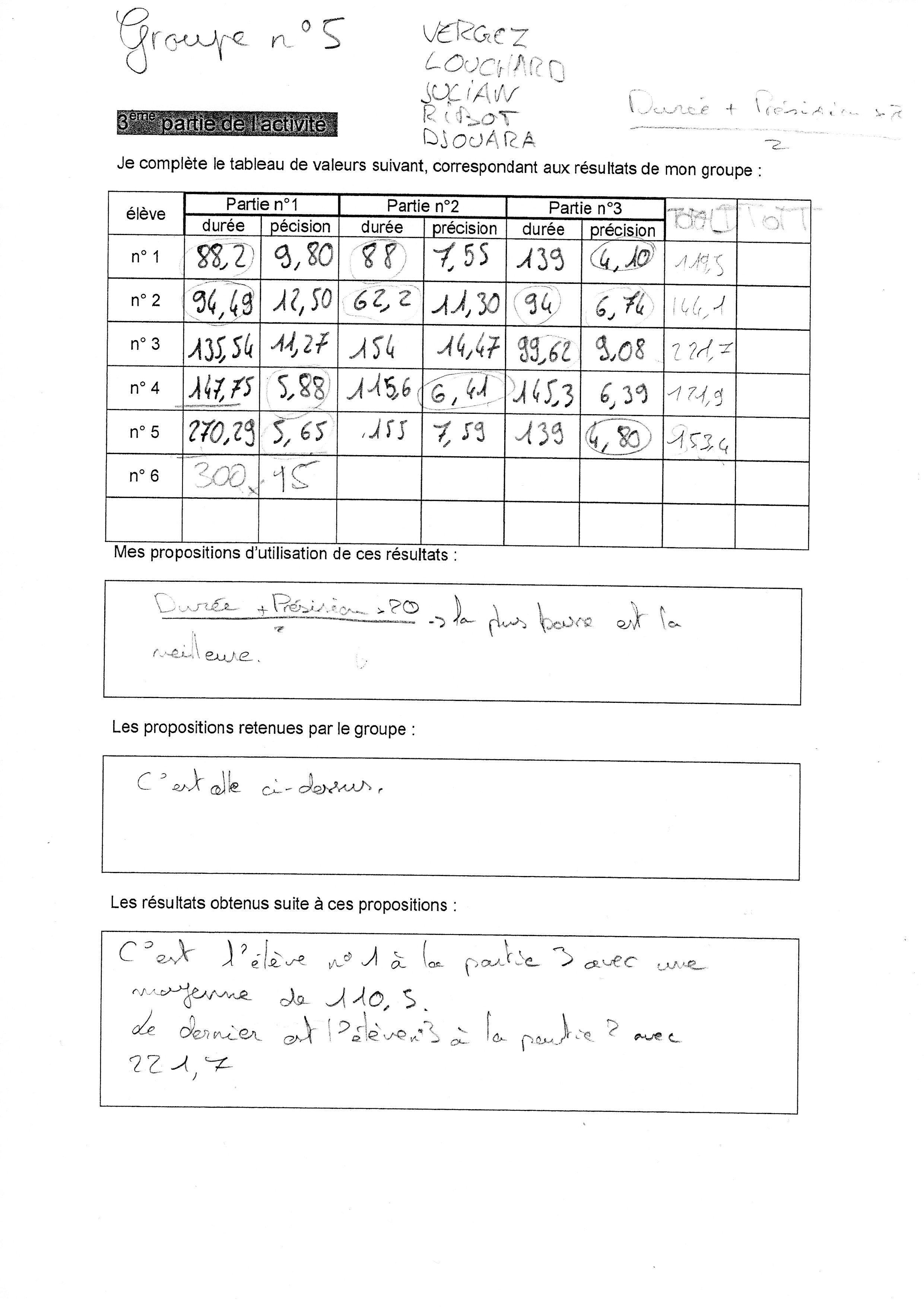
i) Le travail sur les moyennes du temps (T) et de la précision (P) suivant la formule : (T+P)/2
Lors de la 2ème étape, certains groupes ont proposé des calculs de « moyennes » avec le temps et la précision :
Voici quelques exemples de productions d’élèves :


Cependant, pour d’autres groupes, cette moyenne « simple » ne convient pas :

Ils proposent de pondérer cette moyenne :


Un autre groupe se pose la question quel élément prendre en compte en priorité : le temps ou la précision ?

De ce cas, certains élèves s’aperçoivent qu’il y a une différence entre la mesure des deux grandeurs en jeu, donc le choix de multiplier par un (des) coefficient(s), ce qui nous envoie au deuxième point.
ii) Multiplier la précision P par un coefficient : (a*P+T)/a+1
Au cours de leurs réflexions, les élèves ont eu la conviction que dans tous leurs essais avec les données brutes, le temps était très nettement avantagé et que la différence d’ordre de grandeur entre temps et précision devait être compensée d’une façon ou d’une autre.
Ils ont alors pensé à coefficienter chacune des grandeurs de façon à influer sur les deux valeurs pour rétablir un certain équilibre entre elles. En voici quelques exemples :
Classe de seconde :

Le faible écart entre les coefficients choisis n’a, semble-t-il pas permis aux élèves d’être satisfaits des résultats obtenus ; ils ont tenté de modifier les coefficients mais sont chaque fois restés sur des valeurs trop voisines.
Classe de troisième :
Un groupe a proposé de calculer pour chaque jeu effectué le calcul suivant :
![]()
et a ainsi tenté de classer les différents joueurs.
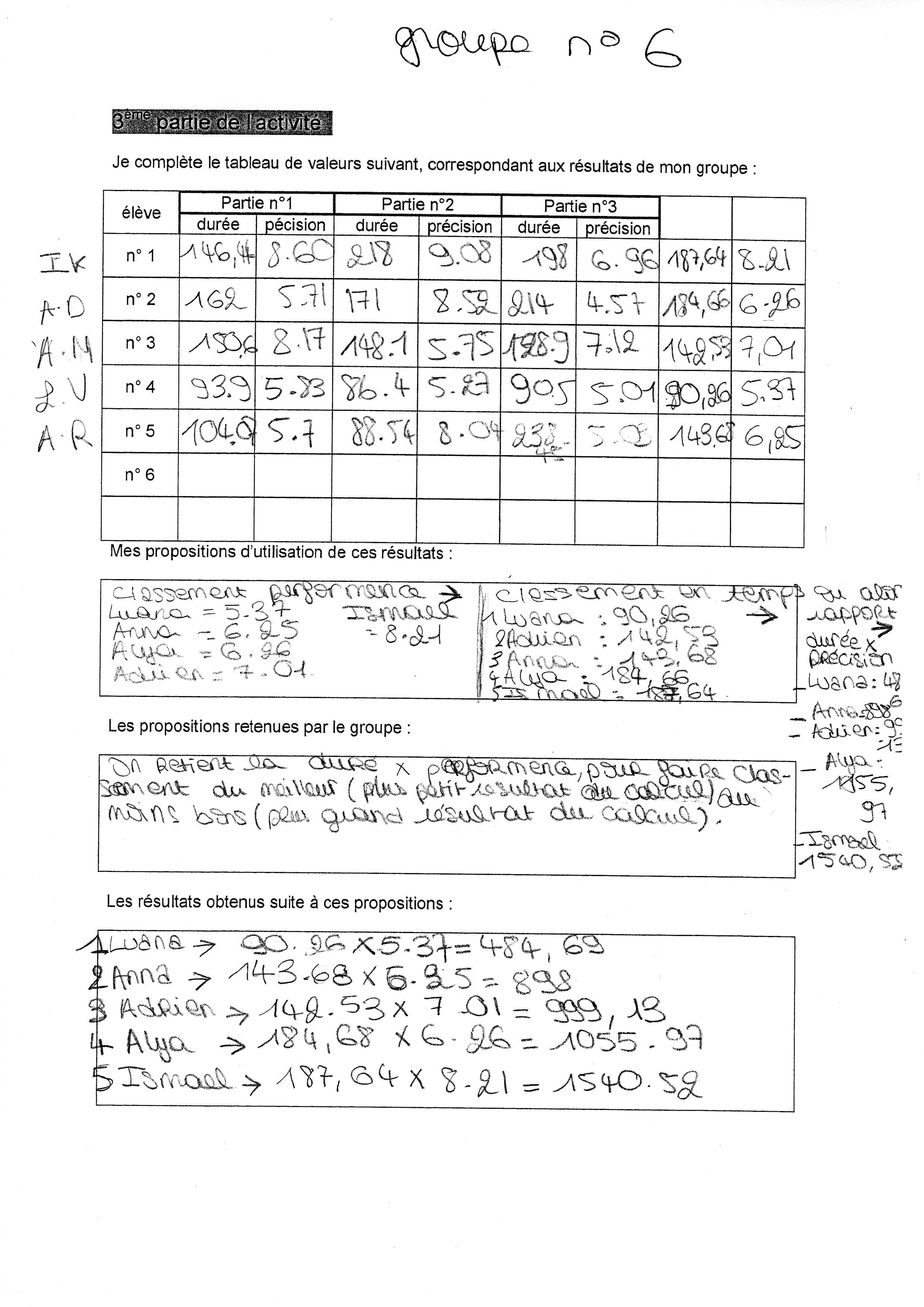
iii) Multiplication des deux grandeurs précision P et temps T, suivant la formule P*T
Plusieurs groupes ont mené en parallèle un même type de réflexion et ont abouti à des solutions similaires ; l’idée force était de comparer les produits « durée moyenne x erreur moyenne » ; leur conclusion était que plus le produit est petit, plus le joueur est performant. Ils ont ainsi réussi à classer les différents membres des groupes. Là encore le problème de la prépondérance de la durée sur la précision a été évoquée dans la discussion mais la recherche d’une solution pour inverser ce phénomène n’a pas été poussée à son terme, surtout en collège. Dans un groupe, le meilleur joueur est encore une fois le plus rapide et aussi le plus précis ; ce fait a conforté les élèves dans leur vision des choses.
Classe de seconde :


Classe de troisième :
4.4 Synthèse
4.4 Synthèse des expérimentations de la ressource
Nous avons mis en évidence, par l’expérimentation, que la mise en œuvre de cette ressource en classe est une partie intégrante du processus de son appropriation. La relation de dépendance entre la stratégie de résolution et les règles du jeu fixés par les joueurs, donne une certaine flexibilité à la ressource et donc à l’enseignant lors de son adaptation pour ses besoins.
Fixer les règles du jeu a priori (c.-à-d. avant de jouer et de récolter les données statistiques), par l’enseignant ou les joueurs, pourraient constituer une nouvelle piste d’expérimentation. L’intérêt de ce choix est qu’il permet de lancer un débat scientifique moins biaisé entre les joueurs.
5. Conclusion
Nous avons présenté dans les différentes parties de ce texte une large palette d’adaptations potentielles de la ressource associée à des activités de recherche d’élèves. Ce travail et le présent texte s’inscrivent dans le principe de la conception dans l’usage. Ils pourraient enrichir les prochaines adaptations et mise en œuvre des enseignants/lecteurs.
Nous soulignons le caractère vivant d’une ressource implémentée dans une plateforme en ligne. Elle subit un travail de construction et de reconstruction des mathématiques dans une ressource en fonction des potentialités de la plateforme, du niveau des élèves et des pratiques de l’enseignant. L’étude de cas présentée (ressource « compas dans l’œil »), illustre la nouvelle philosophie de conception de ressources comme un objet destiné à évoluer, dans une dynamique où le rôle de l’usager est central. Il s’agit donc moins de proposer d’emblée l’objet le plus abouti possible, et susceptible d’évoluer permettre des échanges fructueux et d’engager une dynamique évolutive.
Références bibliographiques
– Artigue, M., Gueudet, G. (2008). Ressources en ligne et enseignement des mathématiques. Conférence à l’Université d’été de mathématiques, Saint-Flour.
– Gueudet, G., & Trouche, L. (2010), Des ressources aux documents, travail du professeur et genèses documentaires, In Gueudet G. et Trouche L. (dir.) Ressources vives. Le travail documentaire des professeurs en mathématiques, pp. 57-74. Collection Paideia, Presses Universitaires de Rennes et INRP.
– Sabra H., Trouche L. (dir.) (2009), Enseignement des mathématiques et TICE, Revue de la littérature de recherche francophone (2002 – 2008), INRP, Lyon, 151 p. En ligne http://ife.ens-lyon.fr/editions/editions-electroniques/enseignement-des-mathematiques-et-tice
Annexe 1
| Annexe 1. Activité professeur - Le compas dans l’œil Que le meilleur gagne ! La situation proposée permet de tester votre capacité à placer au mieux un point qui finalise diverses configurations géométriques particulières telles que milieu d’un segment, parallélogramme, bissectrice, point de convergence de trois rayons lumineux ... Chaque jeu consiste à réaliser trois séries de sept configurations. Le tableau situé sur la partie droite de l’écran de jeu affiche pour chaque question de chaque série l’erreur (mesurée en pixels ou degrés suivant les différentes questions) entre votre choix et la réponse théorique ; il affiche aussi l’erreur moyenne et le temps total réalisé. |