Scratch ne permet pas de colorier directement l’intérieur d’un tracé. Il est par conséquent difficile de tracer des figures « remplies ».
Patrice Debrabant se propose ici d’examiner le cas particulier des figures présentant un caractère d’autosimilarité, figures que l’on peut tracer à l’aide du bloc Estampiller.
Scratch ne permet pas de colorier directement l’intérieur d’un tracé. Il est par conséquent difficile de tracer des figures « remplies ».
On se propose ici d’examiner le cas particulier des figures présentant un caractère d’autosimilarité, figures que l’on peut tracer à l’aide du bloc Estampiller.
L’idée est simple : créer un lutin qui correspondant au motif élémentaire, que l’on retrouve à différentes échelles dans la figure présentant un caractère d’autosimilarité.
Exemple 1 : fractal (napperon) pentagonal de Sierpinski

On commence par créer un image (au format png et sur fond transparent) du pentagone rempli (par exemple en utilisant GeoGebra ou CaRMetal).
Par commodité, on peut faire en sorte que le côté du pentagone soit de 100 px.

On utilise ensuite cette image comme costume d’un lutin.
On va imaginer ici que le pentagone est tracé « main gauche » à partir d’un sommet :

Par conséquent, dans Scratch, on fixe le centre de rotation de la figure à l’origine de la flèche rouge représentée ci-dessus.

Il n’y a plus qu’à créer le script associé à ce lutin.
On utilise une fonction récursive sans utiliser de variables locales à la fonction (pour la bonne raison qu’il n’y en a pas dans Scratch). Tout doit se dérouler dans le passage de paramètres.
Le schéma de la récursion est le suivant :

Les petits pentagones sont dans un rapport $\dfrac{1}{\phi^2} \approx 0,4$ par rapport au pentagone initial. $\phi$ est le nombre d’or, égal à $\dfrac{1+\sqrt{5}}{2}$
En effet, soit $k$ le rapport de réduction.
Pour obtenir un recollement sans chevauchement, on doit avoir :
$k+2.k.cos(72°)+k = 1$
$2k(1+cos(72°))=1$
D’où $k=\dfrac{1}{2(1+cos(72°))}=\dfrac{1}{4.cos^2(36°)}=\dfrac{1}{\phi^2}$ (car $cos(36°)=\dfrac{\phi}{2}$)
On pourra consulter cet article de l’auteur pour plus de précision.
Comme le polygone a un côté de 100 px, le tracer à la bonne dimension consiste à enchaîner :
- Mettre la taille à coteVoulu %
- Estampiller
Le script Scratch est le suivant :

La version avec des étoiles isotoxales est obtenu par un simple changement de costume du lutin.

Exemple 2 : les illusions d’optique d’Akiyoshi KITAOKA
Akiyoshi KITAOKA est un professeur de psychologie japonais auteur d’illusions d’optique comme on peut le voir sur ce site.
A) Un renflement (« A bulge »)

On peut recréer l’œuvre ci-dessus à l’aide de Scratch.
On va cette fois utiliser deux lutins : un lutin costume carré noir et un lutin costume carré blanc. Quand le carré noir noir a terminé sa contribution, il envoie un message au carré blanc qui applique une deuxième couche en superposition sur les carrés noirs. [1]
Pour le reste, c’est un peu « technique » (= faut un peu galérer) si on veut reproduire l’œuvre fidèlement. On pourra consulter le fichier pdf « Cours et exercices/ Bases de Python » (p 43-44) accessible sur cette page web.
On a choisi de travailler en géométrie repérée (avec le bloc Aller à (,) ) plutôt qu’en géométrie de la tortue.

B) Les rayons tournants (« Rotating rays »)

On choisit un lutin avec le costume suivant :
![]()
Enfin, plus exactement on devrait prendre ce costume... En pratique, l’auteur a été obligé de « ruser » et de prendre le costume suivant :

On crée le fond (disque bleu).
On modifie le centre de rotation du lutin.
Pour le script du lutin, on enchaîne six séquences de blocs du type suivant :


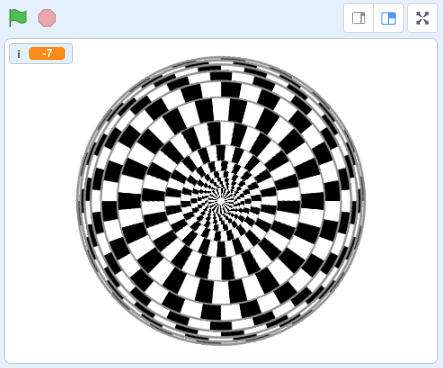
C) « Uzumaki ampan »

Pour cet exemple et le suivant, c’est un peu plus « tiré par les cheveux » car on va prendre un costume en forme de secteur angulaire, que l’on va faire tourner pour restituer un élément ayant une symétrie de rotation.
Le costume (créé avec CaRMetal) est le suivant :

On remarque que sur la figure originale la variation des rayons des cercles correspond (grosso modo) aux variations de la fonction arc tangente (déportée).

On utilise cette fonction pour économiser le code.
On a alors un script très court :

Le résultat est le suivant :

D) « « Rotating snakes » »
Il s’agit de la figure la plus célèbre d’Akiyoshi KITAOKA que l’on peut apprécier sur ce site déjà cité.
La méthode est très similaire à celle utilisée dans l’exemple précédent, à ceci près que l’on mobilise deux lutins.
Le résultat est plus ou moins convaincant...
