« Il y a plus de choses sur la terre et dans le ciel, Horatio,
qu’il n’en est rêvé dans votre philosophie. »
Shakespeare William, La Tragique Histoire d’Hamlet, prince de Danemark, 1601
Remerciement : Je tiens à exprimer toute ma gratitude à Benoît GUY qui s’est chargé d’apporter des améliorations à l’article afin que le lecteur puisse se l’approprier plus aisément.
TABLE DES MATIÈRES
INTRODUCTION
1) DÉTERMINATION DES TRIANGLES GÉODÉSIQUES DE LA CHAÎNE SPATIALE
2) RAPPELS D’ASTRONOMIE
3) LA DIGRESSION DE L’ÉTOILE POLAIRE
4) MESURES AZIMUTALES
5) UTILISATION DE L’ÉTOILE POLAIRE POUR DÉTERMINER L’ANGLE SPHÉRIQUE ENTRE LE MÉRIDIEN D’UN LIEU ET UN ARC DE GRAND CERCLE COUPANT CE MÉRIDIEN.
6) AUTRE APPROCHE N’UTILISANT PAS LE THÉORÈME DE RÉDUCTION À L’HORIZON D’APRÈS UNE IDÉE DE PASCAL QUINTON.
ANNEXES
RÉFÉRENCES
INTRODUCTION : LA TRIANGULATION
Nous nous proposons de montrer dans cet article les aspects mathématiques et astronomiques liés au traitement d’une chaîne spatiale de triangles permettant de mesurer un arc de méridien.
Cet article n’a pas la prétention de retracer l’appareil mathématique utilisé par
Delambre et Méchain au dix huitième siècle mais se veut prétexte à utiliser des
des mathématiques en faisant l’approximation que la terre est sphérique.
On sait que l’ellipsoïde est la manière la plus exacte d’approcher le géoïde
terrestre.
https://fr.wikipedia.org/wiki/G%C3%A9o%C3%AFde
Les géodésiens et astronomes ont mesuré des arcs de $1^\circ$ prés des pôles ou de l’équateur pour mettre en évidence le modèle d’ellipsoïde à retenir.
Newton a émis l’hypothèse d’un sphéroïde oblate dont le petit axe coïncide avec l’axe de rotation de la terre.

- schéma 2
Les différents types de latitude : la querelle des Newtoniens et des Cassiniens.

- schéma 2 BIS
On considère l’ellipse méridienne de $A$. La verticale astronomique de $A$ est la direction du fil à plomb en ce lieu.
L’angle de cette verticale avec le plan équatorial est appelé $\varphi$.
C’est l’angle de $(OA)$ avec le plan équatorial. On le note $\varphi’$.
C’est l’angle de la normale en $A$ à l’ellipsoïde avec le plan de l’équateur.
On le note $\varphi’’$
Nous admettrons que l’écart entre $\varphi’’$ et $\varphi$ n’excède pas $3’’$ et nous considérerons par la suite que $\varphi’’$ et $\varphi$ sont égaux.
On peut démontrer que la latitude géocentrique diffère de la latitude astronomique de moins de 12 secondes.
On peut montrer que si l’on a affaire à un ellipsoïde oblate, c’est-à-dire dont l’axe de rotation est celui du petit axe, alors :
- Si la différence est de $1^\circ$ en latitude astronomique alors l’arc de $1^\circ$ est plus grand au pôle qu’à l’équateur et donc que le sphéroïde est oblate (FIG.2 ter).
- Si la différence est de $1^\circ$ en latitude géocentrique alors l’arc de $1^\circ$ à l’équateur est plus grand qu’au Pôle dans le cas du sphéroïde prolate (FIG.2 ter).
C’est sur cette confusion liée aux latitudes que naquit une querelle entre Cassini et les Newtoniens.
Le modèle de Newton fût validé par les mesures des arcs à l’équateur et au pôle.
On comprend donc l’intérêt de touts ces missions scientifiques fondées sur la triangulation qui ont permis de confirmer les intuitions de Newton.
Nous allons admettre qu’en tout point d’un ellipsoïde, il existe une sphère locale (sphère de courbure moyenne) tangente à l’ellipsoïde en ce point et qui approche au mieux l’ellipsoïde.
Ce résultat est essentiel car localement les triangles géodésiques de l’ellipsoïde, projections des triangle spatiaux seront traités comme des triangles sphériques auxquels on pourra donc appliquer le théorème de Legendre qui permet de résoudre des triangles sphériques en les ramenant à des triangles plans et dont l’énoncé sera formulé plus loin.
Examinons la figure 3.
La sphère représentée est la sphère tangente en $E$ à l’ellipsoïde. Projeter les triangles sur l’ellipsoïde ou sur la sphère locale (résultat dû à Gauss) revient au même pour tout calcul sur ces triangles(admis).
La substitution à l’ellipsoïde de la sphère locale est acceptable en géodésie dans un rayon approximatif de 100 km autour du point de tangence entre l’ellipsoïde et la sphère.
La triangulation vise à établir une chaîne de triangles de part et d’autre du méridien de l’ellipsoïde en suivant le protocole développé ci-dessous.
Pour ce dossier, nous assimilerons la terre à une sphère, ce qui signifie que
nous ne ferons plus appel à la sphére locale.
Protocole de triangulation
Voici les principales étapes de la triangulation.
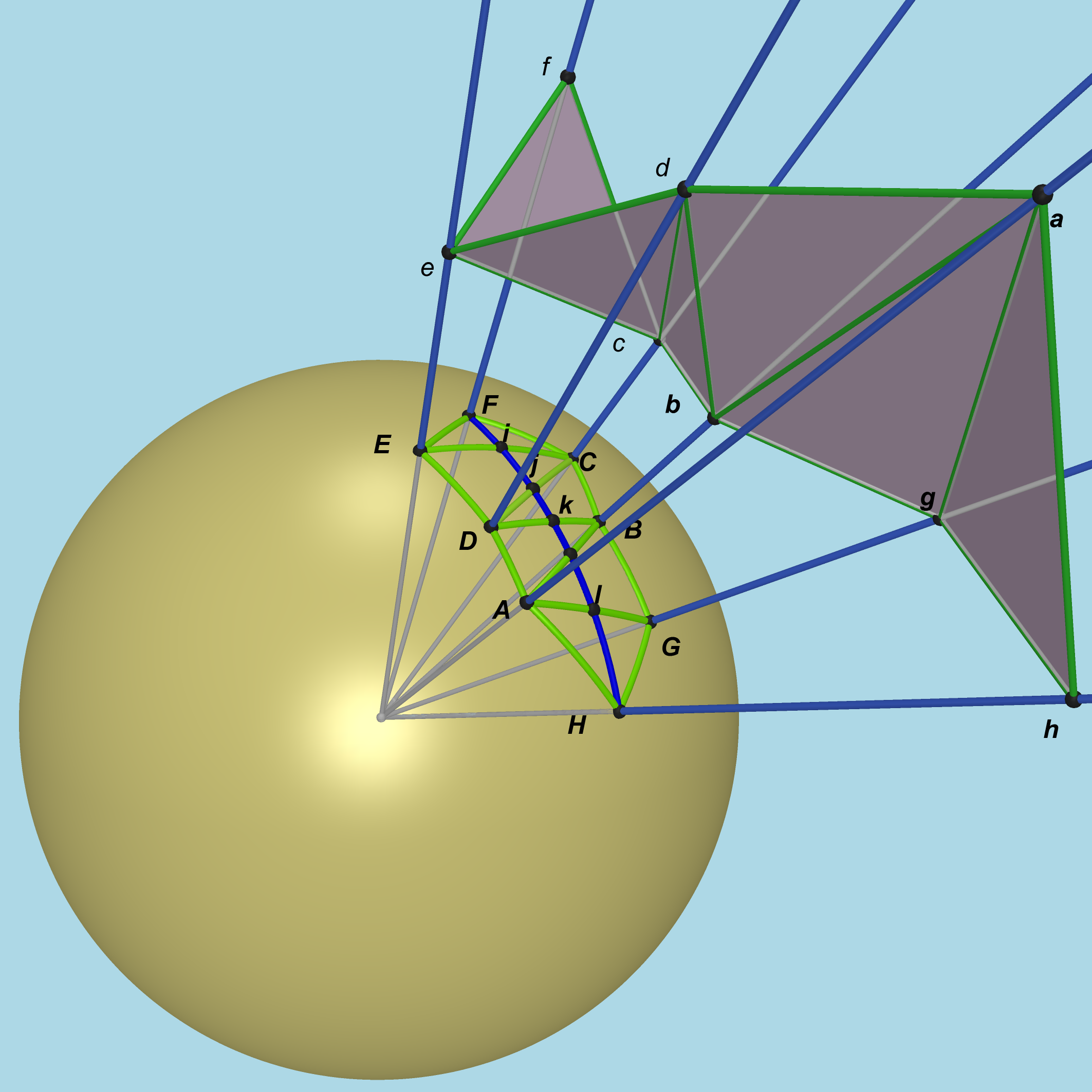
Choisir des points élevés de part et d’autre de l’arc de méridien, (tours, églises, châteaux…) de façon que de chacun de ces points on aperçoive les deux suivants.
C’est la liste de points $e$, $f$, $c$, $d$, $b$, $a$, $g$, $h$ qui ramenés à la sphère locale, fournit les points $E$, $F$, $C$, $D$, $B$, $A$, $G$, $H$.
– Mesurer les angles des triangles par des visées effectuées à l’aide du Cercle répétiteur
– Mesurer une base de l’un des triangles (arpentage).
c) Mesures astronomiques azimutales
– Procéder aux mesures astronomiques pour déterminer l’inclinaison des côtés par rapport à la méridienne.
Il s’agit de déterminer l’inclinaison des côtés des triangles par rapport à la verticale.
Nous expliquerons dans ce qui suit le détail de chacune des étapes précitées, en invoquant le théorème de Legendre ou encore ce que l’on appelle la réduction d’un angle à l’horizon ou encore ce bijou que constitue l’étude mathématique de la digression de l’étoile polaire en prenant les différentielles des formules de Gauss.
ce qui est vraiment merveilleux c’est que pour mesurer la terre, nous nous servirons du ciel.
Cette étude sera l’occasion de faire de la géométrie dans l’espace et de
manipuler les angles dièdres.
Au préalable voici le Cercle répétiteur qui permet de réaliser des mesures d’angle horizontalement et verticalement sur le terrain.
Cercle répétiteur de Jean-Charles de Borda fabriqué par Étienne Lenoir
DÉTERMINATION DES TRIANGLES SPHÉRIQUES
1) Détermination des angles des triangles sphériques de la chaîne géodésique
Nous allons voir que la détermination des angles de la chaîne spatiale permet de connaître les angles des triangles sphériques qui recouvrent la ligne bleue du méridien (figure 3).
Ensuite, il faudra résoudre chaque triangle sphérique ayant mesuré sur le terrain la base de l’un d’entre eux. Et c’est alors que l’on peut se ramener à des triangles plans grâce au merveilleux théorème de Legendre que nous aborderons par la suite.
Nous allons expliciter cette démarche :
Rappels de trigonométrie sphérique
Rappel 1 : Formulaire de trigonométrie sphérique
On se reportera au site suivant : http://media4.obspm.fr/public/AMC/pages_defrepere/formulaire-trigo.html
Rappel 2 : Résolution d’un triangle sphérique dans lequel on connaît les trois côtés
http://pycreach.free.fr/archives/Trigonometrie%20spherique.pdf
Connaissant $a$, $b$ et $c$, le problème admet une solution si et seulement si $|b-c| < a < b+c$ et $a+b+c < 2\pi$.
On a alors :
– $\alpha =\arccos \left( \dfrac{\cos a-\cos b\cos c}{\sin b\sin c}\right) $
– $\beta =\arccos \left( \dfrac{\cos b-\cos c\cos a}{\sin c\sin a}\right) $
– $\gamma =\arccos \left( \dfrac{\cos c-\cos a\cos b}{\sin a\sin b}\right) $
« La connaissance des angles d’un triangle spatial et des mesures zénithales relatives aux côtés de ce triangle permettent de connaître les angles du triangle sphérique correspondant de la sphère locale. »
Démonstration
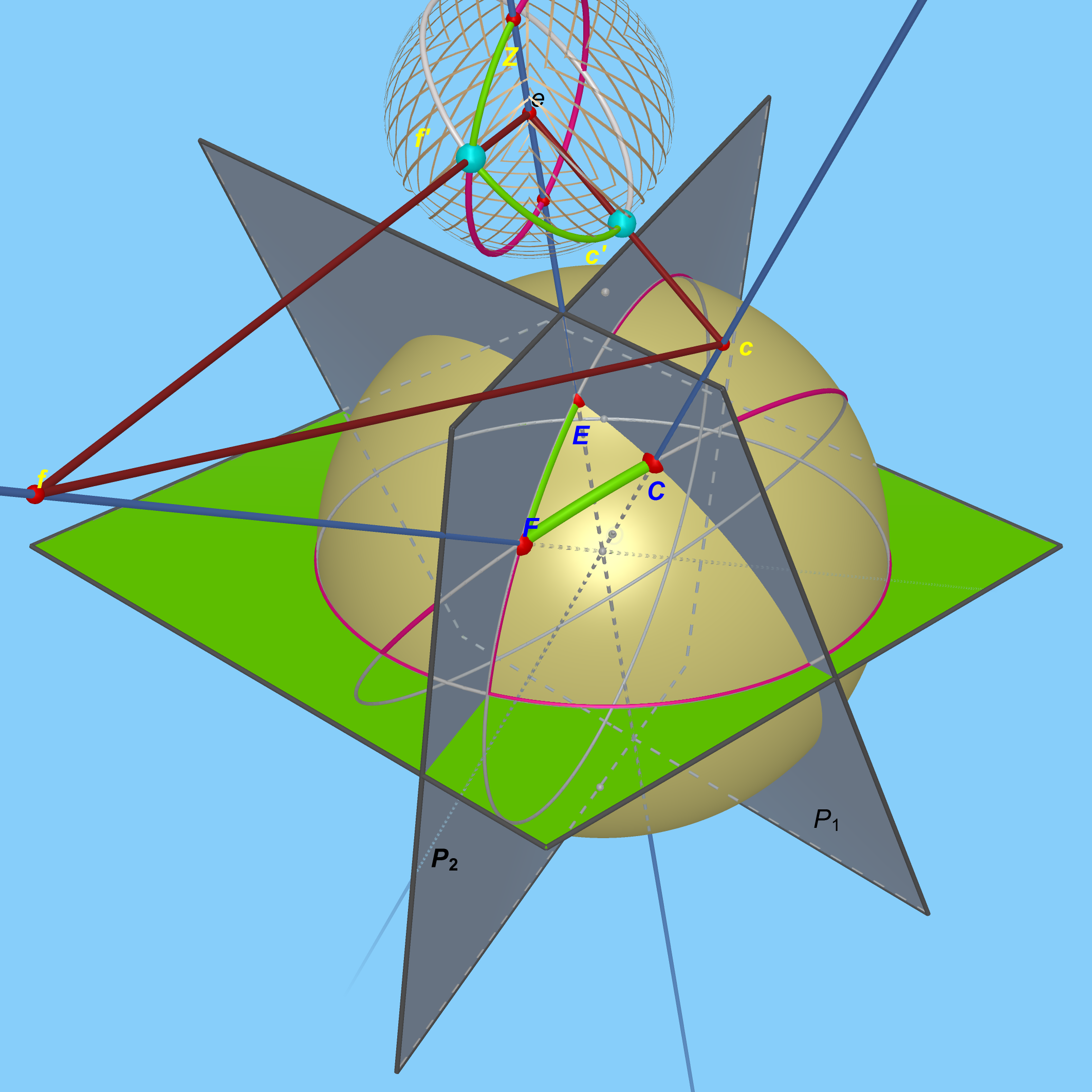
Soient $e$, $f$, $c$ les sommets à partir desquels on fabrique progressivement la chaîne des triangles spatiaux, la sphère en marron foncé est une sphère de rayon arbitraire de centre $e$ que l’on voit par transparence.
$Z$ l’un des points d’intersection de cette sphère avec $(OE)$, $O$ étant le centre de la sphère locale(en marron clair).
$f’$ l’intersection de la demi droite $[ef)$ avec cette sphère.
$c’$ l’intersection de la demi droite $[ce)$ avec cette sphère.
Il est clair que $\widehat{Z}$ du triangle sphérique $f’Zc’=\widehat{E}$ du triangle sphérique $FEC$.
Pour connaître $\widehat{Z}$ nous avons besoin de connaître $\widehat{f’c’}$ et les angles $\widehat{feZ}$ et $\widehat{ceZ}$.
$\widehat{feZ}$ et $\widehat{ceZ}$ relèvent de mesures dites zénithales car il suffit simplement de mesurer l’angle avec la verticale de $A$ des directions $(ef)$ et $(ec)$.
Ainsi grâce à $\widehat{feZ}$ nous connaissons $\widehat{Zf’}$ et grâce à $\widehat{ceZ’}$ nous connaissons $\widehat{Zc’}$.
L’angle $\widehat{fec}$ a été mesuré grâce au Cercle répétiteur et correspond à la mesure $\widehat{f’c’}$.
Nous appliquons alors le rappel 2 de trigonométrie sphérique du paragraphe 1 de trigonométrie sphérique au triangle sphérique $f’Zc’$, ce qui fournit $\widehat{Z}$.
On recommence cette opération pour connaître les 3 angles du triangle $EFC$.
On applique alors au triangle sphérique $EFC$ (
Le théorème de Legendre précise que le calcul d’un triangle sphérique peu étendu se ramène au calcul d’un triangle plan dont les côtés ont même longueur que ceux du triangle sphérique à condition de retrancher à chacun de ses angles $\dfrac{1}{3}$ de l’excès sphérique. Ce théorème est valable pour des triangles jusqu’à 200km de côté.
Excès sphérique$=\alpha+\beta+\gamma-\pi$
De sorte que si l’on connaît la base $EF$, on peut connaître toutes les dimensions du triangle plan $E’F’C’$ construit à partir du triangle sphérique $EFC$ via le théorème de Legendre et lui appliquer les formules de la trigonométrie rectiligne comme la relation des 3 sinus ou le théorème d’Al-Kashi.
N’oublions pas que nous cherchons la longueur $\overset{\frown}{Fi}$ (
Et c’est là que vont intervenir les mesures astronomiques azimutales (cf. c) du protocole de triangulation) qui vont nous permette de connaître l’angle sphérique $\widehat{iFC}$ puis de proche en proche $\widehat{jiC}$ etc.
Ces mesures azimutales relèvent de l’astronomie et plus particulièrement d’une propriété relative à l’étoile polaire appelée propriété de digression.
RAPPELS D’ASTRONOMIE
Les coordonnées horizontales
Crédit : Club d’Astronomie du Lycée Saint Exupéry, Lyon
Crédit : Club d’Astronomie du Lycée Saint Exupéry, Lyon
LA DIGRESSION DE L’ÉTOILE POLAIRE
Angle parallactique : c’est l’angle $S$ du triangle sphérique $PAZ$ avec $Z$ désignant le zénith.
Triangle parallactique ou triangle de position : c’est le triangle sphérique $PAZ$.
$\delta$ désigne la déclinaison de l’étoile, $\varphi$ la latitude, $h$ la hauteur de l’étoile et $a$ l’azimut.
Digression d’une étoile : On dit qu’une étoile est en digression si l’angle parallactique vaut $90º$.
Nous pouvons aussi observer la digression d’une étoile grâce à la simulation proposée sur le site de l’Unité de Formation-Enseignement de l’Observatoire de Paris
On fera varier l’heure TU pour observer le phénomène de digression.
L’azimut passe alors par deux extremums comme il sera démontré en annexe.
La première lettre en rouge est l’azimut a.
Une propriété importante est :
« À la digression de l’étoile polaire, la hauteur de l’étoile polaire est égale à la hauteur du pôle céleste nord autrement dit à la latitude du lieu. »
Cette propriété peut être admise compte tenu de ce que la démonstration proposée en annexe est laissée aux lecteurs aguerris. Cette démonstration est une démonstration classique que l’on trouve par exemple dans la bible qu’est le Danjon d’astronomie.
On pourra alors observer sur le site de l’Unité de Formation-Enseignement de l’Observatoire de Paris que si l’on choisit la latitude $\varphi$ et la déclinaison $\delta$ telle que $|\varphi| < |\delta|$ alors il se produit une digression orientale et une digression occidentale.
Nous aborderons en annexe l’étude mathématique de la digression grâce au calcul différentiel qui nous permettra d’établir l’expression de la dérivée de l’azimut en fonction de l’angle horaire.
LES MESURES AZIMUTALES
La méthode astronomique de détermination des angles entre la méridienne et les côtés de la chaîne de triangle sphériques.
Nous développerons deux démonstrations possibles utilisant l’une le théorème d’Al-Kashi, l’autre le théorème de la réduction d’un angle à l’horizon.
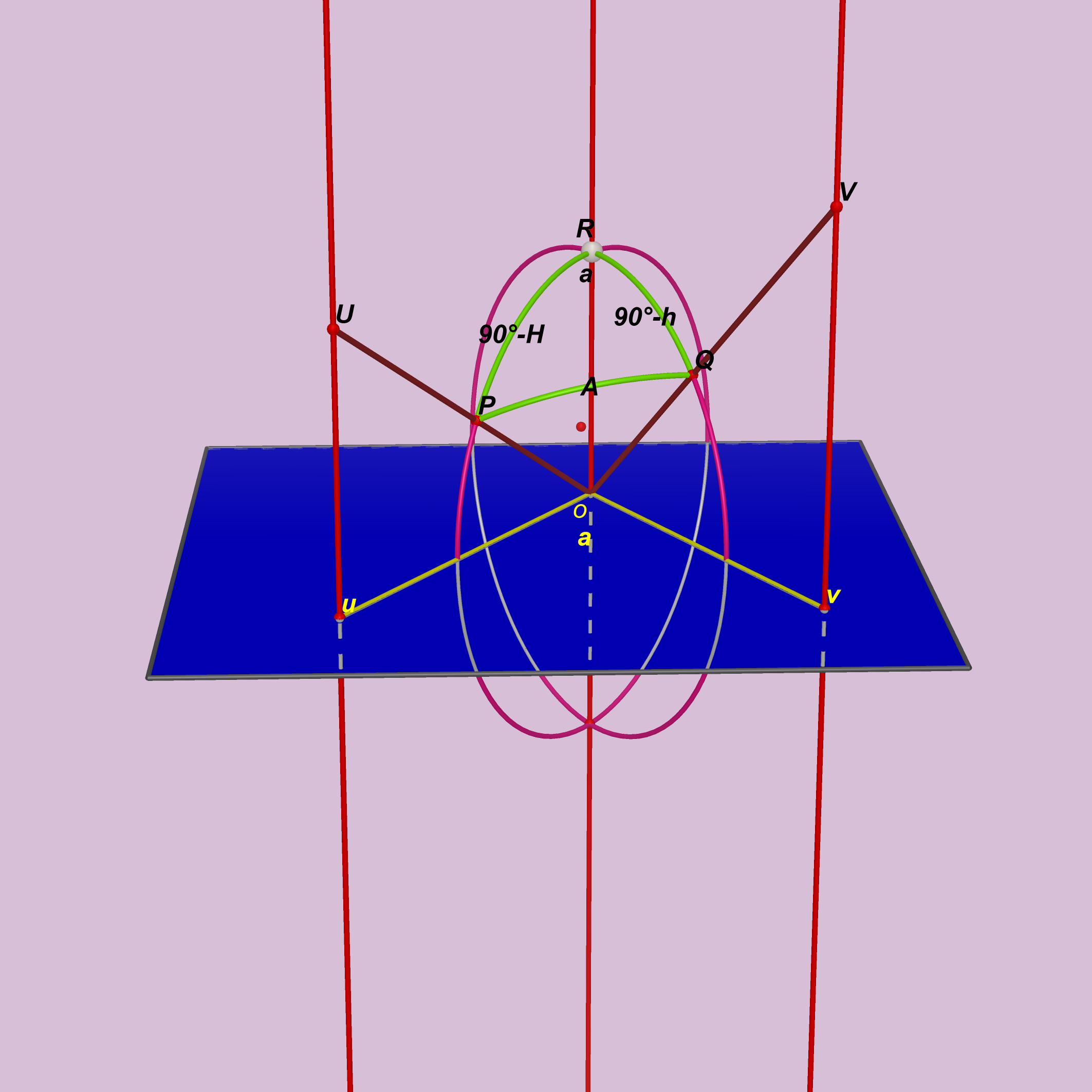
a)Théorème de la réduction à l’horizon
11 bis s’obtient en masquant la sphère de 11.
De quoi s’agit-il ?
Appelons $u$ et $v$ les projetés orthogonaux respectifs de $U$ et $V$ sur le plan bleu.
On pose $\widehat{Uou}=H$ et $\widehat{Vov}=h$
Dans ce cas : $\cos{a} =\dfrac{ \cos{A} − \sin{H} \times \sin{h}}{\cos{H} \times \cos{h}}$ (1)
On mesure grâce au Cercle répétiteur l’angle $\widehat{uov}$ et on effectue les mesures zénithales permettant de connaître les angles $\widehat{Uou}$ et $\widehat{Vov}$.
Démonstration :
Rappel : $\cos{a} = \cos{b} \cos{c} + \sin{b} \sin{c} \cos{\alpha}$
Considérons une sphère fictive (FIG.11 et FIG.11 bis) de centre $o$. Cette sphère coupe $(oU)$ en $P$ et $(oV)$ en $Q$.
Les formules de trigonométrie sphérique permettent alors d’écrire dans le triangle sphérique $PQR$ :
$\cos{A} = \cos {( 90^\circ − h )} \times \cos {( 90^\circ − H )} + \sin {( 90^\circ − h )} \times {\sin ( 90^\circ − H )} \times \cos{a}$
Soit $\cos{A} = \sin{h} \times \sin{(H)} + \cos{h} \times \cos{H} \times \cos{a}$
$\cos{a} =\dfrac{\cos{A} − \sin{H} × \sin{h}}{\cos{H} \times \cos{h}}$
Nous allons à présent sur un exemple montrer comment tirer parti de l’étoile polaire pour déterminer l’angle entre un côté d’un triangle et la méridienne, ce qui nous conduit à examiner le §d) du protocole intitulé mesures astronomiques azimutales.
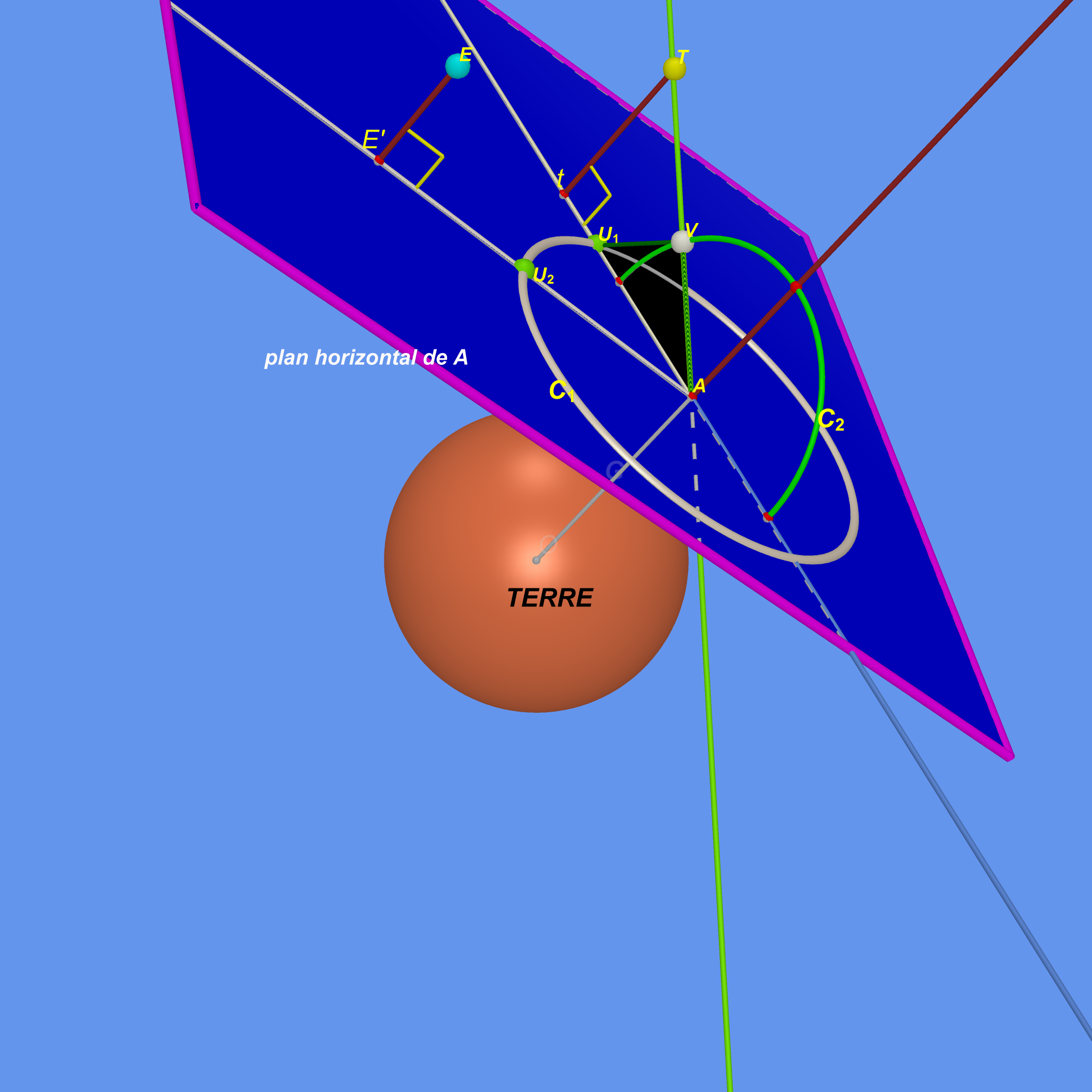
b) Mesure d’angle dans un plan horizontal
Cette mesure peut être effectuée à l’aide d’un théodolite ou du Cercle répétiteur de Jean-Charles de Borda selon le schéma suivant : il s’agit de connaître l’angle $\widehat{tAE’}$.
Le cercle $(C_{1})$ est dans le plan horizontal. Le triangle $U_{1}VA$ est perpendiculaire au plan du cercle $(C_{1})$.
$U_{1}$ est mobile sur le cercle $(C_{1})$. $[AV]$ désigne une lunette de visée. Le point $V$ est mobile sur le demi-cercle $(C_{2})$.
L’observateur vise le point $T$ et recommence en visant le point $E$.
Appelons T et T’ les projections orthogonales respectives de T et E sur le plan
horizontal de A.
On a alors $\widehat{tAE’}=\widehat{U_{1}U_{2}}$
Cette méthode nous permettra de mesurer un angle sur le plan horizontal obtenu comme réduction à l’horizon d’un angle spatial.
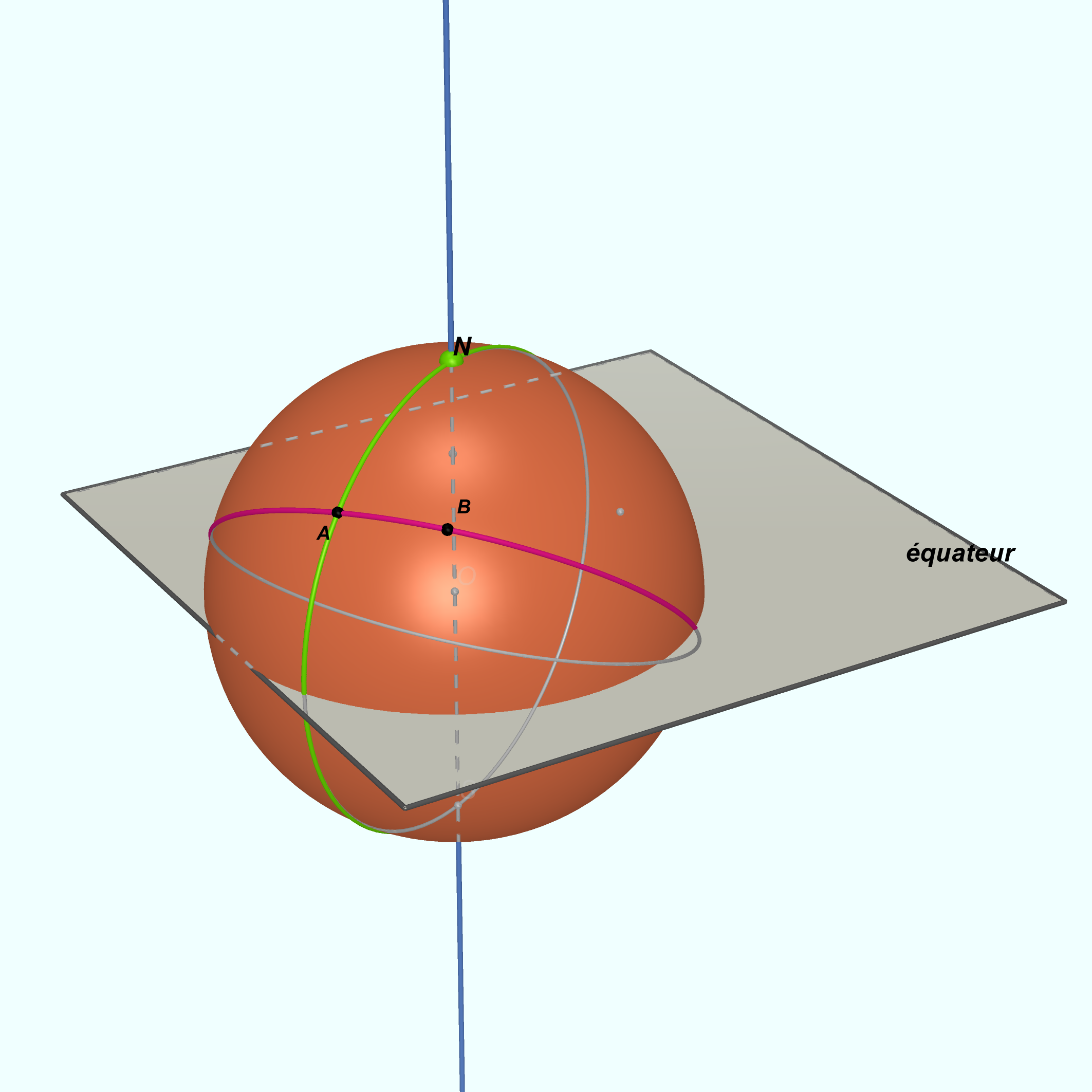
[brun clair]UTILISATION DE L’ÉTOILE POLAIRE POUR DÉTERMINER L’ANGLE SPHÉRIQUE ENTRE LE MÉRIDIEN D’UN LIEU ET UN ARC DE GRAND CERCLE COUPANT CE MÉRIDIEN.[/brun clair]
Je vais proposer une progression dans les schémas qui permettront de mieux comprendre la démonstration.
En vert le méridien de G, A et B deux points de la sphère terrestre. a et b deux points situés à la verticale de A et B.
N le pôle nord terrestre.
Le but de ce paragraphe est de déterminer l’angle $\widehat{A}$ du triangle sphérique $NAB$.
la sphère violette du schéma 15 est la sphère céleste locale de centre $A$. $(ZA)$ et $(ZB)$ sont les zéniths respectifs de $A$ et $B$.
$e$ est une étoile qui parcourt le cercle bleu au cours de la rotation diurne.
Il s’agit du mouvement apparent.
$a$ et $b$ deux points de la chaîne spatiale des triangles (
Les cercles blancs, rouge et vert sont des grands cercles de la sphère céleste.
Le cercle jaune est le cercle horizon de l’observateur $A$.
$n$ est le pôle nord céleste et $N$ le pôle nord terrestre.
Complétons le schéma précédent en masquant la sphère céleste.

- schéma 16
Dans le plan horizontal relatif au point $a$ de la chaîne spatiale, situé sur la demi-droite$[A, ZA]$, le théodolite ou le Cercle répétiteur de Jean-Charles de Borda permet la mesure de l’angle $\overset{\frown}{A’’B’’}$ (schéma 16).
Le point $b$ de la chaîne spatiale de triangles est situé sur la demi-droite$[B, ZB]$
(schéma 18).

- schéma 17
La hauteur du pôle $n$ est égale à la latitude du lieu soit $\varphi$. C’est l’angle $\widehat{nAn’}$.
La hauteur de l’étoile polaire en digression est égale aussi à la latitude $\varphi$ d’après la propriété (P2). C’est l’angle $\widehat{eAv}$.
$\widehat{nAe}$ est égale à $90^\circ -\delta$ avec $\delta$ déclinaison de l’étoile polaire (schéma 17).
En effet la mesure de $\overset{\frown}{ne’}$ est la déclinaison de l’étoile $e$.
L’angle $\widehat{P’’AA’’}$ est la réduction à l’horizon de l’angle $\widehat{nAe}$.
$\cos \widehat{P’’AA’’} = \dfrac{\cos (\delta) - \sin^2(\varphi)}{\cos^2(\varphi)}$
Appliquons la formule (1) plus haut $\cos{a} = \dfrac{ \cos{A} − \sin{H} \times \sin{h}}{\cos{H} \times \cos{h}}$, on a : $\cos{ \widehat{P’’AA’’}} = \dfrac{ \cos{ \delta } - \sin^2{ \varphi}}{\cos^2{\varphi}}$
$\delta$ est une donnée astronomique que l’on peut par exemple obtenir sur Stellarium en rentrant Polaris dans l’outil de recherche. (Voir annexe).
Ainsi nous connaissons l’arc $\overset{\frown}{P’’A’’}$.
D’où $\overset{\frown}{P’’B’’} = \overset{\frown}{P’’A’’} + \overset{\frown}{A’’B’’}$ or $\overset{\frown}{P’’B’’}$ n’est autre que la mesure de l’angle $\widehat{ZA}$ du triangle sphérique $P’’ ZA B’’$.
Or l’angle $\widehat{ZA}$ du triangle sphérique $P’’ ZA B’’$ sur la sphère céleste est aussi égal à l’angle $\widehat{A}$ du triangle sphérique terrestre $NAB$.
Conclusion : il est possible de connaître l’angle entre le méridien terrestre d’un point $A$ et un arc $\overset{\frown}{AB}$ de grand cercle de la sphère terrestre.
Ainsi on peut connaître de proche en proche tous les éléments de la chaîne sphérique et déterminer la longueur d’un tronçon de méridien de la
Le mathématicien Jean-Charles de Borda a calculé que la différence de latitude entre deux points d’un méridien doit être au moins égale à $10^\circ$ pour que le calcul soit représentatif dans le cadre du calcul de la longueur du quart du méridien terrestre nécessaire à la détermination du mètre sous la révolution.
AUTRE APPROCHE N’UTILISANT PAS LE THÉORÈME DE RÉDUCTION À L’HORIZON D’APRÈS UNE IDÉE DE PASCAL QUINTON.
Considérons le schéma 19 qui est une reprise du schéma 16.
À la digression de l’étoile polaire $e$, cette étoile a même hauteur que le pôle céleste $n$, autrement dit les angles $\widehat{eAv}$ et $\widehat{Nan’}$ sont égaux.
Il en résulte que $ev = nn’$
Le quadrilatère $e n P’ A’$ est alors un rectangle et donc $en = A’P’$.
Posons $b =A’’A P’’$, $c = \widehat{eAn}$, $a = \widehat{eAv} = \widehat{Nan’}$
$R$ = le rayon de la sphère céleste.
Le théorème d’Al-Kashi appliqué au triangle $eAn$ permet d’écrire :
$en^2 = 2 R^2 - 2 R^2 \cos c$
Dans les triangles rectangles $eAv$ et $nAn’$, on a : $Av= R \cos a$ et $An’ = R \cos a$
Le théorème d’Al-Kashi appliqué au triangle $Avn’$ permet d’écrire :
$vn’^2 = 2 R^2 \cos^2 a – 2 R^2 \cos^2 a \cos b$
De $en=vn’$, on tire :
$2 R^2 \cos^2a – 2 R^2 \cos^2 a \cos b = 2 R^2 - 2 R^2 \cos c$
D’où : $\cos b = \dfrac{\cos c − \sin^2 a}{cos^2 a}$
$c$ = déclinaison de l’étoile polaire
$a$ = latitude du lieu = hauteur de l’étoile polaire à sa digression.
ANNEXES
A) RAPPEL DE TRIGONOMÉTRIE SPHÉRIQUE
B) ÉTUDE MATHÉMATIQUE DE LA DIGRESSION D’UNE ÉTOILE
C) CALCULS DÉTAILLÉS DE LA TRIANGULATION MENÉE PAR PICARD VERS 1670
D) DONNÉES ASTRONOMIQUES SUR POLARIS
E) CALCUL D’UNE BASE
A) RAPPELS DE TRIGONOMÉTRIE SPHÉRIQUE
On se reportera au formulaire du site de l’Unité de Formation-Enseignement de l’Observatoire de Paris
B) ÉTUDE MATHÉMATIQUE DE LA DIGRESSION D’UNE ÉTOILE
L’angle $\widehat{S}$ est appelé angle parallactique ou angle à l’astre.
Les formules de la trigonométrie sphérique permettent d’écrire dans le triangle $PAZ$ :
-
- $\cos z = \sin \varphi \sin \delta + \cos \varphi \cos \delta \cos H$ (1)
- $\sin z \sin a = \cos \delta \sin H$ (2)
- $\sin z \cos a = -\cos \varphi \sin \delta + \sin \varphi \cos \delta \cos H$ (3)
Par différentiation des relations précédentes, on a en supposant que la déclinaison de l’étoile est constante et que la latitude est invariable :
-
- $dz \sin z = dH \cos \varphi \cos \delta \sin H$ (1bis)
- $da \sin z \cos a + dz \cos z \sin a = dH \cos \delta \cos H$ (2bis)
- $-da \sin z \sin a + dz \cos z \cos a = -dH \sin \varphi \cos \delta \sin H$ (3bis)
Multiplions les deux membres de (2bis) par $\cos a$ et les deux membres de (3bis) par $\sin a$.
On obtient par soustraction membre à membre :
$\sin z \dfrac{da}{dH} = \cos \delta (\cos a \cos H +\ \sin a \sin \varphi \sin H)$
On a par ailleurs $\cos S = \cos a \cos H + \sin a \sin H \sin \varphi$ (4)
$\sin z \cos S = \sin \varphi \cos \delta - \cos \varphi \sin \delta \cos H$ (5)
D’où $\dfrac{da}{dH} = \dfrac{(\cos \delta \cos S)}{\sin z}$ (6)
Remplaçons dans (6) $\cos S$ par son expression tirée de (5)
On obtient $\dfrac{da}{dH}=\dfrac{\cos^2 \delta}{\cos^2 h} \cos \varphi(\tan \varphi - \tan \delta \cos H)$
Nous venons ainsi d’obtenir l’expression de la dérivée de l’azimut par rapport à l’angle horaire $H$.
On a donc les deux cas suivants :
- $|\varphi|\gg|\delta|$, alors $\dfrac{da}{dH}$ garde un signe constant, celui de $\varphi$.
L’azimut croît avec le temps dans l’hémisphère nord et décroît avec le temps dans l’hémisphère sud. - $|\varphi|\ll|\delta|$, alors l’équation $\cos H = \dfrac{\tan \varphi}{\tan \delta}$ a deux racines $H_1$ et $H_2$ avec $H_1$ dans $[0^\circ ;360^\circ ]$ (voir les 2 types de tableau de variation).
D’après l’expression (6) de la dérivée de l’azimut par rapport à $H$
$\dfrac{da}{dH} = \dfrac{\cos \delta \cos S}{\sin z}$ la dérivée s’annulant pour $\cos S=0$.
C’est-à-dire quand le triangle sphérique $PZM$ est rectangle en $S$.
- $\cos c = \cos a \cos b$
- $\sin b = \sin c \sin \beta$
$\sin a = \sin c \sin \alpha \\ \\$ - $\cot c = \cot b \cos \alpha$
$\cot c = \cot a \cos \beta \\ \\$ - $\cot \beta = \sin a \cot b$
$\cot \alpha = \sin b \cot a$ - $\cos c = \cot \beta \cot \alpha$
- $\cos \beta = \cos b \sin \alpha$
$\cos \alpha = \cos a \sin \beta$
La relation (1) permet alors d’écrire en digression que la hauteur $h$ vérifie : $\sin h = \dfrac{\sin \varphi}{\sin \delta}$ (7)
Grâce à la relation du groupe 3 $\cot c = \cot b \cos \alpha$, on peut écrire :
$cos a = −\dfrac{\tan \varphi}{\tan h}$ les 2 azimuts $a_1$ et $a_2$ solutions vérifiant : $a_1 + a_2 = 360^\circ $
Or l’étoile polaire a une déclinaison proche de $90^\circ$.
On a donc $\sin \delta \approx 1$ et par conséquent : $\sin h \approx \sin \varphi$ d’après (7).
D’où $h \approx \varphi$
« La hauteur de l’étoile polaire est égale à la latitude lorsque l’étoile est en digression orientale ou occidentale. »
Les deux types de tableau de variation de l’azimut en fonction de la déclinaison.
Dans les 2 cas $H_1 + H_2 = 360^\circ $.
Premier cas, la déclinaison est positive : $\delta > 0$
Deuxième cas, la déclinaison est négative : $\delta < 0$
C) CALCULS DÉTAILLÉS DE LA TRIANGULATION MENÉE PAR PICARD VERS 1670
Picard a fait tous ses calculs en supposant tous les triangles dans un même plan horizontal, c’est à dire en négligeant la sphéricité de la terre.
La toise de Paris dite toise du grand Châtelet est égale à $1,949$m.
Cette approximation fait que tous les méridiens sont sensiblement parallèles et de plus latitude de $V$ = latitude de $V’$ et latitude de $E$ = latitude de $E’$.
En fait, les méridiens qui sont des cercles se confondent localement avec leurs tangentes.
Picard projette orthogonalement $EG$, $GK$, $KN$ et $VN$ sur le méridien.
Détermination de EG
EXERCICE
Étape 1
1) Triangle $ABC$
$\widehat{CAB}= 54^\circ 4’35’’$
$\widehat{ABC}= 95^\circ 6’55’’$
$\widehat{ACB}= 30^\circ 48’30’’$
$AB = 5633$ toises
Calculer $AC$ et $BC$
2) Triangle $ADC$
$\widehat{DAC}= 77^\circ 25’50’’$
$\widehat{ADC}= 55^\circ 0’10’’$
$\widehat{ACD}= 47^\circ 34’0’’$
Calculer $DC$ et $AD$
3) Triangle $DEC$
$\widehat{DEC}= 74^\circ 9’30’’$
$\widehat{DCE}= 40^\circ 34’0’’$
$\widehat{CDE}= 65^\circ 16’30’’$
Calculer $DE$ et $CE$
4) Triangle $DCF$
$\widehat{DCF}= 113^\circ 47’40’’$
$\widehat{DFC}= 33^\circ 40’0’’$
$\widehat{FDC}= 32^\circ 32’20’’$
Calculer $DF$
5) Triangle $DFG$
$\widehat{DFG}= 92^\circ 5’20’’$
$\widehat{DGF}= 57^\circ 34’0’’$
$\widehat{GDF}= 30^\circ 20’40’’$
Calculer $DG$ et $FG$.
6) Triangle $GDE$
$\widehat{GDE}= 128^\circ 9’30’’$
Calculer $DG$ et $DE$
En déduire $GE$.
Etape 2
Les points $E$, $G$, $K$, $N$ et $V$ constituent des points choisis par Picard pour effectuer sa triangulation.
La ligne rouge représente le méridien de $N$. La méthode du § c) permet à Picard de connaître (FIG.22) les angles AeG, aQkg, aK’NK et aVNV’. Ce sont des mesures azimutales.
La méthode de triangulation pour calculer $EG$ peut être recommencée avec $KG$, puis $NK$ et enfin $VN$.
On projette alors orthogonalement les points $E$, $G$, $K$, $V$ sur le méridien et l’on connaît ainsi $E’G’$, $G’K’$, $K’N$ et $NV’$ d’où la connaissance de longueur de méridien $E’V’$.
Picard trouve alors :
- $\widehat{VNV’}=18^\circ 55’$, $\widehat{KNK’}= 2^\circ 9’10’’$, $\widehat{Qkg}= 1^\circ 9’$, $\widehat{aEG}= 0^\circ 26’$,
- $GE= 31895$ toises, $NK= 17564$ toises, $KG= 17564$ toises et $NV= 18907$ toises.
EXERCICE
Calculer alors la longueur
EXERCICE
Les calculs précédents ne supposent pas la terre sphérique mais plane sur une
surface peu étendue.
Picard trouve ente Malvoisine ($V$) et Amiens ($E$) une différence de latitude de $1^\circ 22’ 55’’$ (Voir FIG.23).
Malvoisine est le point $E$ ; Amiens est le point $V$ (FIG.21).
Si l’on fait l’hypothèse d’une terre sphérique, déterminer dans ce cas la longueur de la circonférence terrestre.
Après diverses corrections, Picard retient la valeur de $78850$ toises pour la longueur du méridien entre Malvoisine et Amiens qui correspondent aux points $V’$ et $E’$.
D) DONNÉES ASTRONOMIQUES SUR L’ÉTOILE POLAIRE
E) CALCUL D’UNE BASE
Il arrive qu’il soit impossible de mesurer directement la distance entre deux extrémités d’une base. Dans ce cas il faut utiliser un triangle auxiliaire et lui appliquer le théorème d’Al-Kashi.
Soit un triangle $ABC$ dont on veut connaître la distance $d=BC$ connaissant $AB$, $AC$ et $dA$ , $A$ étant proche de $180^\circ $.
On a $d^2 = b^2 + c^2 - 2bc.\cos A$
$d^2 = (b+c)^2 - 2bc - 2bc.\cos A$
$d^2 = (b+c)^2 - 2bc\left(1+\cos A\right)$
$d^2 = (b+c)^2 - 4bc.\cos^2\left(\dfrac{A}{2}\right)$
$d^2 = (b+c)^2\left(1-\dfrac{4bc.\cos^2\left(\dfrac{A}{2}\right)}{\left(b+c\right)^2}\right)$
Posons $x=\dfrac{4bc.\cos^2\left(\dfrac{A}{2}\right)}{(b+c)^2}$ (1)
Comme $A$ est voisin de $180^\circ $, $\dfrac{A}{2}$ est voisin de $90^\circ $ et $x$ est alors voisin de $0$.
$d = (b+c) \times \sqrt{1 − x} \approx (b+c) \times \left(1−\dfrac{x}{2}\right)$
À l’époque de Delambre, on disposait de tables de logarithmes et (1) se prêtait bien au calcul avec logarithme.
RÉFÉRENCES
FILMOGRAPHIE
- le film documentaire de Axel Engstfeld sur l’expédition de Delambre et Mechain dont le but était par triangulation de rattacher le mètre au méridien terrestre. Il disponible sur Daily motion en deux parties :
- La vidéo sur le site de l’ENS de Lyon qui relate l’aventure géodésique ayant permis de mettre fin à la querelle entre les cartésiens et les newtoniens.
BIBLIOGRAPHIE
- Jean-Jacques Levallois, MESURER LA TERRE, 300 ans de géodésie française de la toise du Châtelet au satellite, Presses École Nationale des Ponts et Chaussées
- J. LEFORT, L’aventure cartographique, BELIN (pour la science).
- André DANJON, Astronomie générale, Librairie scientifique et technique Albert BLANCHARD
SUR LE WEB
- Levallois, J.-J., La Géodésie et ses problèmes fondamentaux, L’Astronomie, Vol. 75, p.465
- Jean Baptiste Joseph Delambre, Adrien Marie Legendre, Méthodes analytiques pour la détermination d’un arc du méridien
- « Un Homme à la Mesure du mètre »
- « GÉOMÉTRIE, MESURER LA TERRE, MESURER LA TERRE ? »
- M. Delambre, Histoire de l’astronomie au dix huitième siècle
Dans le même numéro
par Francine Athias
par Lisa Rougetet
par Jean-Pierre Archambault
par Hédi Abderrahim
par Groupe Rénovation de la voie professionnelle de l’IREM d’Aix-Marseille