Dans cet article, on revient sur un des exercices qui ont été posés lors de la première année d’expérimentation de la future épreuve pratique de mathématiques au Bac S. Le sujet choisi porte le numéro 3, et décrit un problème d’optimisation. L’énoncé demande expressément d’utiliser un logiciel de géométrie pour construire la figure et conjecturer la réponse au problème posé. Dans la deuxième partie, il est demandé de vérifier la validité de cette conjecture par des calculs exacts.
On propose ici un corrigé de l’exercice avec la calculatrice Classpad de Casio, dont les qualités en font un outil adapté à la préparation à la nouvelle épreuve. Le Classpad « embarque » en effet un certain nombre d’applications très générales (calcul formel, géométrie dynamique, tableur) ou dédiées à des situations plus spécifiques (études de suites, d’équations différentielles, statistiques, coniques, tracés de courbes ou de surfaces, etc.).
Toutes ces applications coopèrent très facilement. Le symbole même de cette intégration est l’environnement « eActivity », qui permet de lier entre eux des appels aux différentes applications, et de produire ainsi de véritables séquences pédagogiques.
L’intérêt d’un outil réunissant plusieurs aspects majeurs des « mathématices » est évident, notamment quand les environnements correspondants ont été pensés pour dialoguer entre eux, comme c’est le cas ici. À cela s’ajoute, dans le cas d’une calculatrice, le plaisir de pouvoir travailler où bon vous semble, avec un outil toujours disponible. Puisqu’on demande aux élèves un peu plus d’autonomie, qu’on souhaite cultiver en eux le goût de l’initiative, qu’on attend qu’ils fassent des conjectures et qu’ils « expérimentent » les mathématiques plutôt que de toujours les subir, une calculatrice performante comme le Classpad constitue une alternative séduisante.
Pour en revenir à la correction de l’exercice, on a indiqué les étapes (sans pour autant rentrer trop dans le détail) d’une construction géométrique qui ne prend que deux ou trois minutes avec la calculatrice. On propose ensuite deux méthodes pour conjecturer la réponse au problème posé :
– Animer la figure, avec mise à jour automatique des mesures qui permettent de deviner la solution de l’exercice. Cette partie est la plus visuelle ; elle est relativement classique et reproductible dans tout logiciel de géométrie dynamique.
– Exporter les données relatives à l’animation précédente dans l’application tableur, où on finalise les calculs ; un nuage de points donne alors une idée synthétique de la situation. L’intérêt pédagogique de cette approche tient dans la facilité avec laquelle on transmet les informations numériques de l’application « géométrie » à l’application « tableur ».
L’énoncé demande ensuite de prouver la validité de la conjecture par un calcul exact. On a donc effectué ces calculs « à la main », avant de les reproduire dans l’environnement de calcul formel (c’est d’ailleurs l’occasion de s’affranchir des hypothèses de longueur imposées par l’énoncé, et de constater que le résultat demandé est valable pour un rectangle plus général).
On termine par un prolongement de l’exercice. On voit à cette occasion que l’outil informatique, s’il facilite le raisonnement purement géométrique, ne s’y substitue pas.
Pour finir sur une note plus personnelle, je précise que j’ai récemment placé sur www.mathprepa.fr des « propositions de corrigés » (toujours avec le Classpad) pour 25 des 27 exercices de l’expérimentation 2006/2007, ainsi que des documents pour l’oral 2 du Capes de mathématiques.
ɉnoncé (sujet n°3 de l’expérimentation 2006/2007)
On décide de mettre en place un système de collecte des eaux de pluie sur la façade d’une maison.
Sur cette façade, de forme rectangulaire, deux tuyaux obliques doivent récupérer les eaux de
pluie pour les déverser dans un tuyau vertical aboutissant à un réservoir. On donne ci-dessous le plan de cette façade ainsi que quelques dimensions, exprimées en mètres.

Sur ce plan :
– $\textrm{[}AM\textrm{]}$ et $\textrm{[}BM\textrm{]}$ représentent les deux premiers tuyaux
– $\textrm{[}MH\textrm{]}$ représente le troisième tuyau
– $\left( MH\right) $ est la médiatrice de $[DC]$.
On souhaite trouver la position du point $M$ sur la façade de cette maison qui permet de minimiser la longueur des tuyaux à acheter et donc la dépense à effectuer.
On note $Q$ le projeté orthogonal de $M$ sur $\left( BC )\right) $ et on prend comme variable la mesure en radians de l’angle
$ \widehat{QMB}$ = $\theta$ (note de l’auteur : ou, ce qui revient au même, l’angle $ \widehat{ABM}$)
-
- Utiliser un logiciel de géométrie pour simuler la situation décrite précédemment.
- En déduire une valeur approchée au centième de la valeur de θ qui rend minimale la longueur des tuyaux. Déterminer, grâce au logiciel, une valeur approchée au centième de la longueur minimale totale des tuyaux.
Appeler l’examinateur pour une vérification de la construction et des réponses trouvées.
- On définit la fonction $g$ par $g(\theta) ={2}MA+MH$ sur l’intervalle $]0 ; \frac{\pi}{2}[$
- On note $g’$ la fonction dérivée de $g$. Démontrer que $g’(\theta)$ = 5 $\frac{2\sin(\theta) - 1} {\cos(\theta)^2}$.
- Déterminer la valeur exacte de $\theta$qui minimise la longueur des tuyaux ainsi que la dépense à prévoir.
Production demandée
– Les réponses attendues dans la question 1.
– Les démonstrations attendues dans la question 2.
Construction de la figure avec le Classpad
A partir de l’écran d’accueil du Classpad (fig1), on lance l’application « géométrie ».
On démarre une nouvelle figure avec « Fich/Nouveau ».
On a représenté ci-dessous (fig2a à fig2d) quelques-uns des menus de l’application (un contact du stylet suffit à sélectionner un outil). On devine à quoi correspondent chacune de ces icônes. Les menus « Fich », « Edit », « Aff » et « Tracé » complètent cet environnement.
 fig1 : l’écran d’accueil |
 fig2a : sélection, zoom |
 fig2c : insérer une figure |
 fig2b : tracé d’objets |
 fig2d : transformations |
On crée un rectangle (choisir l’outil idoine, puis toucher la surface de l’écran avec le stylet).
Les sommets de ce rectangle (qui occupe pour l’instant la totalité de l’écran) sont automatiquement nommés $A,B,C,D$ comme indiqué fig3 (pour se conformer aux notations de l’énoncé, nous les renommerons par la suite).
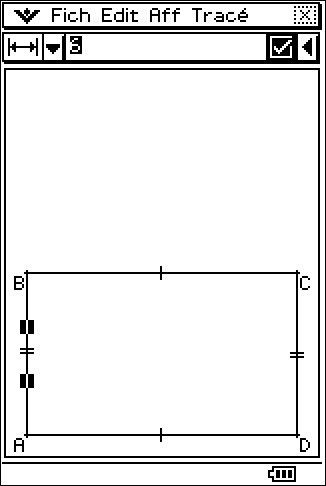
On sélectionne un coté horizontal et on impose la largeur ${10}$. On impose de même la hauteur 6 (fig4). On marque les milieux $E,F$ des cotés horizontaux, puis on trace $[EF]$ (fig5).
 |
 |
 |
| fig3 : le rectangle initial | fig4 :$ABCD$ dimensionné | fig5 : le segment $[EF]$ |
On trace un segment reliant $B$ à un point $G$ de $[EF]$, puis les segments $[CG]$ et $[EG]$ (fig6).
On crée les conditions d’une animation de $G$ sur $[EF]$ en sélectionnant ce point et ce segment puis en choisissant la fonction « Edit/Animer/Ajouter Animation » (fig7).
Par défaut, une animation s’effectue en 20 étapes (on conserve ce paramètre, qui pourrait être modifié au moyen de « Edit/Animer/ɉditer Animations »).
Pour rendre la figure plus conforme encore au modèle, on cache le point $F$ et le segment $[EF]$ (menu « Edit/Propriétés/Caché ») et on renomme les points pour respecter les notations de l’énoncé. Enfin, on marque l’angle $ \widehat{ABM}$ (fig8).
 |
 |
 |
| fig6 : $G$ sur $[EF]$ | fig7 : définir l’animation | fig8 : figure complète |
À ce stade, on peut tester l’animation, soit en utilisant « Edit/Animer/Lancer », soit en affichant le curseur d’animation avec « Aff/Animation UI » comme on l’a fait ici (voir fig9 à fig11, où on a représenté trois étapes).
 |
 |
 |
| fig9 : une étape... | fig10 : ...une autre... | fig11 : ...encore une |
Un peu de géométrie dynamique
Nous allons voir une méthode toute entière inscrite dans l’environnement « géométrie » et qui montre les possibilités de calcul du Classpad à l’intérieur d’une figure (sans exporter les données issues de l’animation, ce qui fera l’objet de la deuxième méthode).
Remarque : il n’a pas été nécessaire de construire $Q$ pour obtenir une mesure de $ \widehat{{BMQ}}$, puisque cet angle est égal à $ \widehat{ABM}$(qui est l’angle que nous avons marqué).
On crée un champ contenant la longueur $MA.$ C’est très simple : on sélectionne le segment $[AM]$, on passe à la deuxième barre d’icônes par un appui sur ’, et on touche l’icône représentant une longueur (ou alors on choisit la fonction « Tracé/Mesure/Longueur »). Il reste alors à renommer ce champ (« AM= » plutôt que « Longueur : ») et à le positionner. On crée ensuite le champ contenant la longueur $MH$ (fig12).
Il reste à calculer ${2}MA+MH.$ Pour cela, on sélectionne la fonction « Tracé/Expression ».
Les différentes expressions présentes sur la figure (ici l’angle $ \widehat{ABM}$ et les mesures $MA$ et $MH$) apparaissent alors numérotées, et l’utilisateur est invité à définir l’expression à calculer. On rentre ici 2@2+@3 qui désigne la quantité ${2}MA+MH$ (fig13).
 |
 |
 |
| fig12 : $MA$ et $MH$ | fig13 : expr. calculée | fig14 : ${2}MA+MH$ |
On renomme cette expression en « 2MA+MH » (fig14).
On affiche le menu d’animation (« Aff/Animation UI »), ce qui permet de dérouler l’animation en mode automatique ou manuel. A chaque étape, les données de la figure sont actualisées, ce qui donne une première approche de la façon dont la quantité ${2}MA+MH$ dépend de l’angle $\theta$(fig15,16,17).
En exécutant cette animation pas à pas, on constate que le minimum de la somme ${2}MA+MH$ vaut approximativement 14,66 et que cette valeur est obtenue au voisinage immédiat de $\theta$=30°.
 |
 |
 |
| fig15 : $MA$ et $MH$ | fig16 : expr. calculée | fig17 : ${2}MA+MH$ |
De la géométrie au tableur
Nous allons voir comment collecter les données issues de l’animation et les exporter (pour les explorer, les traiter ou les confronter éventuellement à un modèle) dans l’application « statistiques » ou dans l’application « tableur » (c’est elle que nous utiliserons ici). Nous revenons pour cela à la contruction telle qu’elle apparaît figure 8.
On sélectionne le segment $[MA]$. Dans la deuxième partie de la barre d’icônes, on visualise sa longueur, avant de toucher l’icône : : avec le stylet, ce qui a pour effet d’envoyer automatiquement (dans la première colonne d’une table apparaissant dans une demi-fenêtre en parallèle de la construction) les longueurs $MA$ correspondant aux différentes phases de l’animation (fig18). On fait ensuite de même avec le segment $[MH]$ : les longueurs correspondantes sont envoyées dans la deuxième colonne de la table (fig19).
On sélectionne les segments $[AB]$ et $[BM].$ on peut visualiser la mesure de l’angle $\theta$ = $\widehat{ABM}$ c’est-à-dire celle de l’angle $\widehat{QMB}$ (rappelons qu’il n’est pas nécessaire de construire le point $Q$). On touche l’icône : : avec le stylet, ce qui a pour effet d’exporter les différentes valeurs de l’angle $\theta$ (correspondant aux 20 étapes de l’animation) dans la troisième colonne (fig20).
 |
 |
 |
| fig18 : valeurs de $MA$ | fig19 : valeurs de $MH$ | fig20 : valeurs de $ \widehat{ABM}$ |
On active la fenêtre de la table et on choisit « Edit/Tout sélectionner », puis « Copier » (fig21).
On passe ensuite dans l’application « tableur », où on colle (« Edit/Coller ») le tableau des données.
À ce stade, la colonne C contient les valeurs de l’angle $\theta$, alors que les colonnes A et B contiennent respectivement les longueurs $MA$ et $MH$ correspondantes (fig22). On positionne le curseur sur la cellule D1, et on choisit la fonction « Edit/Remplir Echelle ». On renseigne la fenêtre de dialogue comme indiqué fig23. Cela signifie qu’on va placer les valeurs ${2}MA+MH$ dans la colonne D (rappelons que l’animation a produit une série de 20 triplets $MA,$$MH,$ $\theta$).
 |
 |
 |
| fig21 : copier la table | fig22 : coller dans tableur | fig23 : calcul${2}MA+MH$ |
On voit le résultat de ce calcul fig24. On sélectionne ensuite les colonnes C et D (qui rappelons-le contiennent les valeurs $\theta$ et ${2}MA+MH$). On choisit de visualiser ces données sous la forme d’un nuage de points (on voit fig25 qu’on a vraiment un choix important de représentations graphiques).
Le nuage de points est tracé immédiatement. On peut maximiser la fenêtre graphique et zoomer sur le nuage de points avec la fonction « Aff/Cadre de zoom ». On peut ensuite sélectionner les différents points du nuage, considérer leurs coordonnées, et constater à nouveau que c’est vers $\theta$=30° que la valeur de ${2}MA+MH$ est minimum, et que ce minimum vaut environ 14,66 (fig26).
 |
 |
 |
| fig24:les ($\theta$,${2}MA+MH$) | fig25 : choix du graphe | fig26 : nuage de points |
Utilisation du calcul formel
Les deux méthodes précédentes semblent indiquer que c’est pour $\theta$=30° (environ) que la quantité ${2}MA+MB$ est minimum, mais la précision est moyenne. Pour connaître cet angle avec une erreur relative de 1%, il suffirait d’augmenter le nombre d’étapes (100 au lieu de 20, par exemple).
En revanche, la valeur minimum de ${2}MA+MB$ semble bien égale à 14,66 au centième près.
Le calcul formel va nous permettre de nous en assurer.
Nous commençons par résoudre l’exercice « à la main ».
Comme le demande l’énoncé, on pose $g(\theta) =MA+MB+MH={2}MA+MH.$
Il est clair que $MA = MB = \frac{BI}{\cos(\theta)} = \frac{5} {\cos(\theta)}$.
De même $MH = IH - IM - BI \times \tan(\theta)$. On en déduit $HM =6 - 5\tan(\theta)$.
Ainsi $g(\theta) =\frac{10} {\cos(\theta)} + 6 - 5\tan(\theta) $.
Il en découle : $g’(\theta) =\frac{{10}\sin(\theta)}{\cos(\theta) ^2}-\frac{5}{\cos(\theta)^2} = {5}\frac{{2}\sin(\theta) - 1} {\cos(\theta)^2}$.
L’angle $\theta$ varie de 0 à l’angle $\theta_{0}$ de $]{0} ; \frac{\pi}{2}[$ défini par $\tan(\theta_{0}) =\frac{CB}{CH}=\frac{6} {5}$ donc $\theta_{0} \approx {50} ^\circ .$
Le signe de $g’(\theta)$ est celui de $\sin(\theta) - \frac{1}{2} = \sin(\theta) - sin(\frac{\pi}{6})$.
Ainsi $g$ est strictement décroissante sur $[{0 ; }\frac{\pi}{6}]$ et strictement croissante sur $[\frac{\pi}{6} ; \theta_{0}]$.
Le minimum de $g$ est atteint en $\theta= \frac{\pi}{6}$ et vaut $g(\frac{\pi}{6}) = \frac{20} {\sqrt{3}} + {6} - \frac{5}{\sqrt{3}} = {5}\sqrt{3} + {6} \approx {14,66}$.
Les calculs précédents peuvent être repris dans l’application « principale » du Classpad.
Mieux, nous allons vérifier que c’est toujours pour $\theta$=30° que la quantité ${2}MA+MH$ est minimum, indépendamment des dimensions (largeur $l$ et hauteur $h$) du rectangle $ABCD.$
En notant $I$ le milieu du segment $AB,$ on a $IC=\frac{l}{2}$ (c’est la demi-longueur).
Ensuite $MB$ est égal à $\frac{IB}{\cos(\theta)},$ puis $MI=IB \times \tan(\theta)$ et $MH=h - MI$.
Cela conduit à l’expression $g = {2}MB + MH$ = $h - \frac{l \times \tan(\theta)}{2} + \frac{l}{\cos(\theta)}$ (fig27).
On calcule la dérivée $g’(\theta)$ et on vérifie qu’elle s’annule pour $\theta= \frac{\pi}{6}$ (il est clair que cette dérivée est négative avant cette valeur, positive après).
On obtient la valeur du minimum de $g(\theta)$ : c’est $g(\frac{\pi}{6}) = h + l\frac{\sqrt{3}}{2}$.
Pour $h={6}$ et $l={10}$, on retrouve bien l’expression ${5}\sqrt{3} + {6}$ (fig28).
 |
 |
| fig27 : définition de $g$ | fig28 : le minimum de $g$ |
On peut adopter une autre approche, en utilisant cette fois la longueur $MI=x$ comme paramètre (rappelons que $I$ désigne ici le milieu du segment $AB$). Voir fig29 et fig30.
 |
 |
| fig29 : autre méthode... | fig30 : ...résultat identique |
Prolongement de l’exercice
On vient de voir qu’on pouvait s’affranchir de la condition (imposée par l’énoncé initial) sur la largeur et la hauteur du rectangle $ABCD$. On peut encore généraliser l’exercice initial dans les termes suivants.
| Soit $M$ un point intérieur au rectangle $ABCD$. Soit $H$ la projection orthogonale de $M$ sur le coté $CD$. Déterminer la position de $M$ qui minimise la somme $MA+MB+MH$. |
La réponse est donnée par la figure ci-après :
– Si on fixe la hauteur de $M$ au-dessus de $[DC],$ et si on note $A’$ le symétrique de $A$ par rapport à l’horizontale passant par $M,$ on voit que $MA+MB=A’M+MB \geq A’B$ (avec égalité seulement si $M$ est en $K$, sur la médiatrice $[IJ]$ de $[AB]$).
– Mais $A’B=KA’+KB=KA+KB={2}KB$ et $MH=KJ$.
– Ainsi $MA+MB+MH \geq {2}KB+KJ$.
– Si $N$ est le point de $[IJ]$ tel que $ \widehat{ABN}={30} ^\circ $, on sait que ${2}KB+KJ \geq {2}NB+NJ$ (avec égalité seulement si $K$ est en $N$).
– Conclusion : l’unique position de $M$ qui minimise $MA+MB+MH$ est en $N$ (cela suppose que $N$ soit intérieur au rectangle $ABCD$, c’est-à-dire que l’angle $ABJ$ soit au moins de mesure 30° ; dans le cas contraire, c’est $J$ qui réalise le minimum de la quantité étudiée).

fig31 : géométrie, le retour |
Remarque :
La figure précédente indique aussi quel $M$ maximise la quantité $g\left( M \right) =MA+MB+MH$
En effet, si on fixe la hauteur de $M$ au-dessus de $CD$, on a $MA+MB+MH=MA’+MB+ED$ et cette quantité est maximum quand $M=E$ (ou $M=F$, par symétrie par rapport à $[IJ]$).
Elle vaut alors $AE+ED+EB={6}+EB$.
Enfin cette dernière quantité est maximum quand $E=D$ (donc quand $M=D$ ou $M=C$).
Elle vaut alors ${6}+\sqrt{{6}^2+{10}^2}={6}+{2}\sqrt{34} \approx{17,662}$.
Une visualisation en 3D
Nous allons terminer cet article par un détour dans l’environnement « Graphe 3D » du Classpad.
On reprend la généralisation de l’exercice ($M$ est quelconque dans le rectangle $ABCD$) mais pour fixer les idées on pose (comme dans l’énoncé initial) $AB={10}$ et $AD={6}$.
Avec les notations de la figure précédente, la position du point $M$ dans le rectangle $ABCD$ est parfaitement déterminée par les quantités $x=AE$ et $y=DH$ (avec ${0} \leq x \leq {6}$ et ${0} \leq y \leq {10}$).
On a alors $MA=\sqrt{x^2+y^2}$, $MB=\sqrt{x^2 + ({10} - y)^2}$ et $MH = {6} - x$.
Ainsi la quantité à minimiser est $g(x,y) = MA + MB + MH = {6} - x + \sqrt{x^2 + y^2} + \sqrt{x^2 + ({10} - y)^2}$, avec les conditions ${0} \leq x \leq {6}$ et ${0} \leq y \leq {10}$).
Dans l’éditeur de « Graphe 3D », on crée $z_{1}(x,y) = {6} - x + \sqrt{x^2+y^2} + \sqrt{x^2+(y - {10})^2}$ (fig32).
On règle les intervalles de la fenêtre graphique : ${0} \leq x \leq {6}$, ${0} \leq y \leq {10}$, et ${14} \leq z \leq {18}$ (fig33).
On trace la surface par un simple contact du stylet sur l’icône « 3Dxyz » (fig34). On peut maximiser la fenêtre de tracé, et se déplacer sur la surface (fonction « Analyse/Tracé »). On peut changer le point de vue de l’observateur en « tirant » la surface avec stylet sur l’écran, ou en modifiant les angles $\theta$(longitude) et $\phi$ (colatitude) dans la fenêtre de choix des paramètres de tracé.
 |
 |
 |
| fig32 : définir $z_{1}\left( x,y \right) $ | fig33 : définir la fenêtre | fig34 : tracé de la surface |
 |
 |
| fig35 : deux autres... | fig36 : ...points de vue |
Bien sûr, le tracé n’est ici qu’une simple illustration de l’énoncé précédent, mais il permet de conjecturer l’existence et l’unicité d’un point $M$ réalisant le minimum de $MA+MB+MH$. En se déplaçant le long des points du réseau (les coordonnées apparaissent au bas de l’écran), on « ressent » presque physiquement comment la valeur de $MA+MB+MH$ dépend de la position de $M$ dans le rectangle $ABCD$.
On en vient à la fin de cet article, qui nous a permis de mobiliser plusieurs environnements de la calculatrice au service d’un même exercice, tant dans une phase de conjecture (géométrie dynamique, en collaboration éventuelle avec le tableur) que dans la validation de cette conjecture par le calcul formel, pour enfin utiliser une application de tracé de surface dans une généralisation de l’énoncé initial.
Vous trouverez sur le site de Jean-Michel Ferrard trois fichiers html contenant chacun un fichier swf. Ces swf sont des fichiers audio-vidéo reprenant les phases successives de la construction géométrique de l’article. Voici les trois pages en question :
– http://www.mathprepa.fr/sujet3/sujet3a.html
– http://www.mathprepa.fr/sujet3/sujet3b.html
– http://www.mathprepa.fr/sujet3/sujet3c.html