Dans cet article, Francine Athias met en évidence comment un logiciel de géométrie dynamique, tel que Tracenpoche, peut conduire dans certains cas l’élève (et le professeur) à distinguer le dessin et la figure. Elle s’appuie sur les spécificités de ce logiciel. Pour une expérimentation en cycle 3, cinq situations de géométrie ont été construites, incluant la géométrie dynamique, à l’aide des modes d’intégration (Assude, 2007). Deux situations sont présentées dans l’article. Puis, sur une de ces situations, l’auteur montre, à l’aide du modèle du jeu, que le jeu que jouent les élèves n’est pas forcément celui qui est attendu (Sensevy, 2011).
Le lecteur intéressé pourra consulter avec profit les ouvrages cités en référence, notamment Athias F. 2014, thèse téléchargeable ici.
Dans cet article, Francine Athias met en évidence comment un logiciel de géométrie dynamique, tel que Tracenpoche, peut conduire dans certains cas l’élève (et le professeur) à distinguer le dessin et la figure. Elle s’appuie sur les spécificités de ce logiciel. Pour une expérimentation en cycle 3, cinq situations de géométrie ont été construites, incluant la géométrie dynamique, à l’aide des modes d’intégration (Assude, 2007). Deux situations sont présentées dans l’article. Puis, sur une de ces situations, l’auteur montre, à l’aide du modèle du jeu, que le jeu que jouent les élèves n’est pas forcément celui qui est attendu (Sensevy, 2011).
Le lecteur intéressé pourra consulter avec profit les ouvrages cités en référence, notamment Athias F. 2014.
Présentation de l’auteur :
Formatrice à l’ESPE de Besançon, Francine Athias intervient essentiellement en Master MEEF pour les étudiants qui veulent devenir professeur des écoles. Par ailleurs elle a soutenu une thèse sur l’introduction de la géométrie dynamique au cycle 3, thèse téléchargeable ici.
NDLR.
Cet article peut être librement diffusé à l’identique dans la limite d’une utilisation non commerciale suivant la licence CC-by-nc-nd
http://creativecommons.org/licenses/by-nc-nd/3.0/fr/legalcode
1- Introduction
Mon expérience en ESPE dans la formation initiale et continue des professeurs des écoles m’a permis de me rendre compte des difficultés à enseigner la géométrie à l’école primaire. Différentes voies étaient possibles pour essayer d’y réfléchir. Le choix que j’ai fait est de m’intéresser à la géométrie dynamique, comme un autre moyen de donner à voir les relations géométriques pour les élèves de cycle 3, en parallèle à l’environnement papier-crayon. J’ai choisi d’utiliser le logiciel Tracenpoche pour mener une expérimentation. Dans une première partie, j’expliciterai le rôle des représentations graphiques en géométrie. Dans une deuxième partie, j’exposerai les raisons du choix de ce logiciel. Dans une troisième partie, je présenterai les éléments théoriques qui ont été le support de construction des situations : j’illustrerai par deux exemples de situations. Dans une quatrième partie, je proposerai les éléments théoriques qui ont permis de décrire et d’analyser les situations : à l’aide de cette modélisation, je montrerai le travail de deux élèves. Enfin, je conclurai.
2 - Dialectique dessin-figure

La pratique de la géométrie à l’école primaire s’appuie sur des représentations graphiques d’objets géométriques. Les propriétés géométriques sont présentées dans l’environnement papier-crayon à travers l’usage des instruments usuels, tels que la règle graduée ou non, l’équerre ou le compas. Dans les curriculums officiels, le terme de géométrie instrumentée est proposée. Cette manière de présenter les objets géométriques n’est pas toujours accessible aux élèves. À titre d’exemple, dans les classes, nous avons rencontré de nombreux élèves qui ont pour tâche le tracé de deux droites perpendiculaires. Le professeur attend une technique spécifique, celle d’utiliser l’équerre pour réaliser le tracé : l’équerre est le signe de la prise en compte de la perpendicularité par les élèves. Cette technique experte repose donc sur un discours mathématique implicite, porté par l’instrument. La représentation graphique obtenue sera nommée figure [1], en tant que représentation graphique prenant en compte les propriétés mathématiques à travers l’usage d’un instrument adéquat. Or, de nombreux élèves parviennent à faire le tracé uniquement avec la règle : ils ont « retenu » ce que sont deux droites perpendiculaires et sont capables de le faire perceptivement. Dans ce cas, la représentation graphique obtenue sera nommée dessin, en tant que représentation graphique qui n’est pas obtenue avec les instruments adéquats. La plupart des élèves prennent leur équerre après la construction et vérifient qu’ils ont effectivement tracé un angle droit. Mais comment la technique des élèves peut-elle évoluer dans ces conditions ? Notre hypothèse de travail consiste à introduire un logiciel de géométrie dynamique pour conduire l’élève à faire l’expérience de la nécessité des propriétés géométriques. Le contexte de la géométrie dynamique nous conduit à préciser les notions de dessins et de figures. Soit la construction à l’écran est définie à partir des propriétés géométriques, et dans ce cas, c’est une figure. Toutes les représentations graphiques à l’écran ont les mêmes propriétés. Soit la construction est faite sans déclarer les propriétés géométriques adéquates, et dans ce cas, c’est un dessin. De notre point de vue, cela signifie que l’ambiguïté de la représentation graphique obtenue à l’écran est levée. Le contrôle de cette différence de statut passe par le déplacement : le déplacement des points déplaçables donne à voir différentes représentations graphiques qui possèdent les mêmes propriétés dans le cas de la figure. A contrario, si la représentation graphique obtenue à l’écran au cours du déplacement des points ne conserve pas les propriétés attendues, il s’agit d’un dessin.
NDLR : Ci-dessus l’illustration du propos de l’auteur. La droite (d2) est perpendiculaire à la droite (d1) au sens de la figure Tracenpoche. En revanche la droite (d3) n’est pas perpendiculaire à la droite (d1) au sens de la figure Tracenpoche même si elle peut être perçue comme perpendiculaire du point de vue du dessin.
Si on bouge certains points (D ou E par exemple) le « dessin » ne résiste pas, et les droites (d1) et (d3) ne sont donc pas perpendiculaires.
3 - Le logiciel Tracenpoche
est retenu pour trois raisons essentielles. Comme dans de nombreux logiciels de géométrie dynamique, différents menus sont accessibles. La première raison du choix de ce logiciel concerne les boutons disponibles dans ces menus, qui sont d’abord présentés par une icône. Si un menu est déroulé, plusieurs boutons sont proposés. Par exemple, dans le menu des « droites particulières », différentes icônes sont proposées (cf illustration 1).

- illustration 1
Le perceptif est donc premier, en lien avec les habitudes des élèves. Reconnaître d’abord l’icône de la propriété avant de tracer. La seconde raison du choix de ce logiciel tient au bandeau jaune explicatif et évolutif. Lorsque le menu est déroulé, le déplacement du curseur sur une des icônes fait apparaître la relation géométrique correspondant à l’icône : par exemple, « construire une droite passant par un point et perpendiculaire à une droite ». Lorsque l’icône est sélectionnée, le message devient plus précis : « Droite passant par le point ? Perpendiculaire à ? Cliquer sur un point ou une direction ». Le point ou la droite peuvent être sélectionnés, sachant qu’un élément sélectionné devient rouge : il n’y a pas d’ambiguïté. Puis, si par exemple, le point A est sélectionné et validé, le bandeau jaune est modifié : « Droite passant par le point A et perpendiculaire à ? Cliquer sur une droite (ou segment ou demi-droite) ». Lorsque la direction a été sélectionnée avec le même codage de couleur, la droite ainsi définie (dans l’exemple, la droite perpendiculaire à (AB) et passant par le point A) apparaît à l’écran, avec le codage de l’angle droit (cf illustration 2).
La représentation graphique obtenue à l’écran est alors une figure : le déplacement des points déplaçables donne à voir toutes les représentations graphiques, avec la même propriété. Dans l’exemple développé, la droite obtenue reste perpendiculaire à la droite (AB) quelque soit le déplacement des points A ou B (vous pouvez faire l’expérience vous même en manipulant les points A et B sur la figure ci-dessus et créer les illustrations 3 et 4).
La troisième raison du choix de ce logiciel tient également à la facilité de prise en main du logiciel relativement aux actions de sélection. La sélection d’un objet géométrique passe par un code couleur : si le point A est sélectionné, il devient rouge (cf illustration 5). Il est validé par un simple clic, et il redevient bleu (cf illustration 6). Lorsqu’un bouton est activé, il ne l’est que pour une fois, c’est-à-dire si la perpendiculaire à (AB) est finalisée, le bouton perpendiculaire n’est plus actif (cf illustration 7). Si l’on souhaite tracer une deuxième perpendiculaire, il faut de nouveau sélectionner ce bouton.
4 - Éléments théoriques pour la construction des situations
4.1 - Modes d’intégration
Des recherches ont permis d’analyser des expérimentations, relatives à l’intégration d’un logiciel de géométrie dynamique en cycle 3. En particulier, la recherche de Assude (2007) a apporté des résultats en termes d’indicateurs a posteriori, qui permettent d’évaluer le degré d’intégration. Pour cela, elle définit les modes d’intégration comme « les différentes manières dont l’intégration se fait et qui exprime l’état ou l’action de cette intégration dans les pratiques des professeurs et des élèves » (Ibid.). Elle présente trois modes [2], le mode d’emploi, le mode d’action et le mode de relation. Nous avons choisi ces modes d’intégration en tant qu’indicateurs a priori pour concevoir les cinq situations.
Les modes d’emploi décrivent la manière dont l’intégration du logiciel est proposée. Assude présente trois modes d’emploi : initiation instrumentale, renforcement instrumental, symbiose instrumentale. Les moments d’initiation instrumentale correspondent au moment où les connaissances instrumentales sont peu nombreuses : l’attention des élèves est plutôt tournée vers la manière d’utiliser le logiciel. Les moments de renforcement instrumental représentent les moments où les connaissances instrumentales sont de mieux en mieux maîtrisées. Les moments de symbiose instrumentale sont les moments où les connaissances instrumentales sont suffisamment maîtrisées pour proposer des situations plus denses du point de vue mathématique. Les cinq situations que nous avons conçues tiennent compte de cette progression : la première et la troisième sont des moments d’initiation instrumentale. La deuxième est un moment de renforcement instrumental. Les deux dernières sont des moments de symbiose instrumentale. Les boutons « perpendiculaire » et « point sur » sont utilisés dans la première situation. Dans la deuxième s’ajoute le « point d’intersection ». Dans la troisième situation, la nouvelle connaissance instrumentale concerne le déplacement de points, sur une construction déjà faite. Les deux dernières n’utilisent pas de nouvelles connaissances instrumentales.
Les modes d’action décrivent la manière dont l’intégration du logiciel est combinée avec le travail mathématique. Assude présente deux modes d’action : un mode d’action dépendant ou un mode d’action d’entrelacement. Nous avons choisi d’organiser le travail mathématique dans l’environnement papier-crayon, puis dans l’environnement Tracenpoche et pour finir dans l’environnement papier-crayon. Autrement dit, dans les cinq situations, nous alternons les environnements.
Les modes de relation décrivent la manière dont l’intégration du logiciel est en lien avec ce qui se passe dans l’environnement Tracenpoche. Assude présente trois modes de relation : ancien, nouveau, juste distance. Nous avons retenu un mode de juste distance pour la plupart des situations. Seule la situation 3 est dans un mode nouveau : le déplacement pour voir des propriétés sur une construction faite par autrui n’a pas d’équivalent dans l’environnement papier-crayon.
4.2 - Exemple : la situation 1
Description
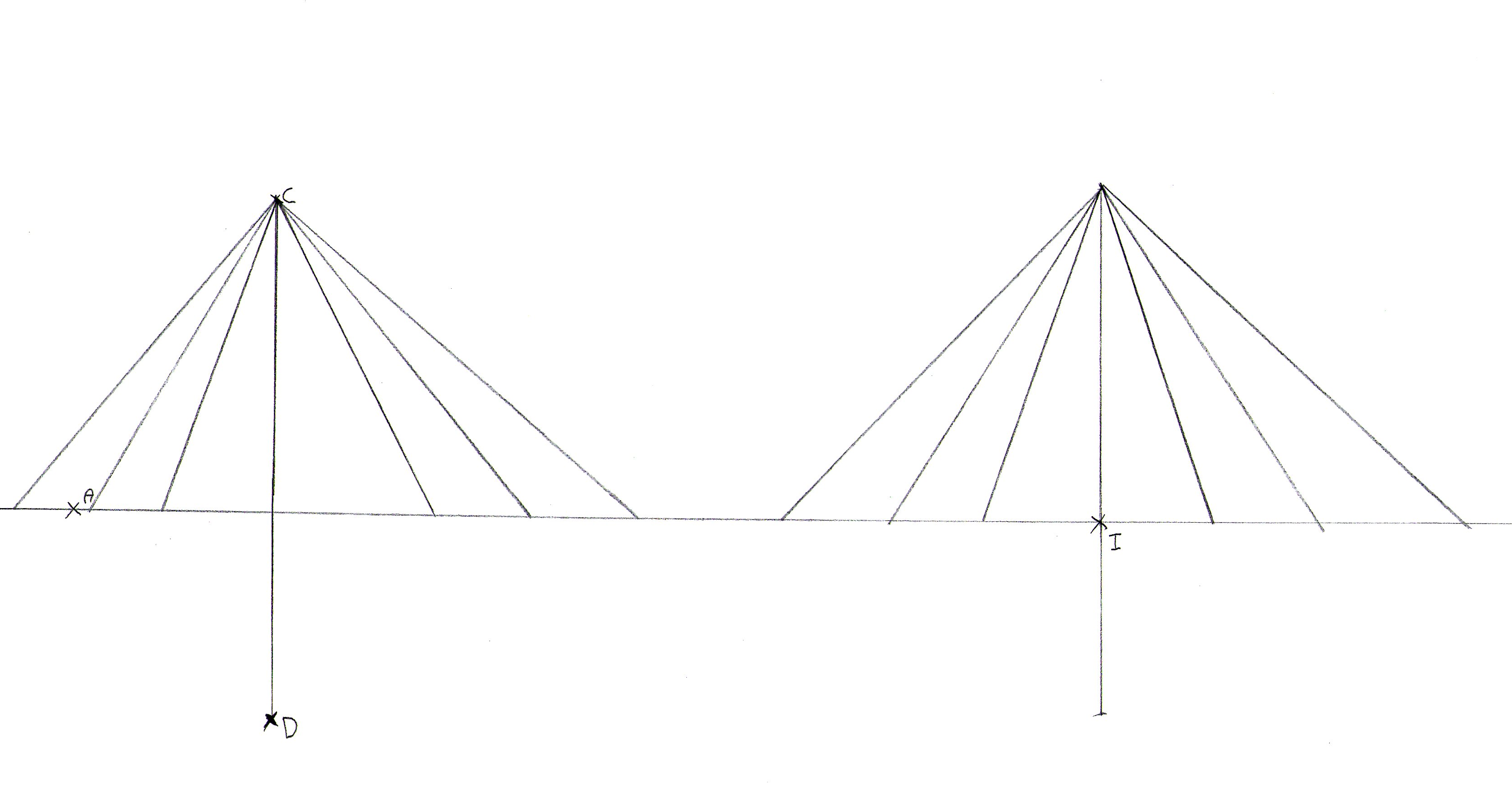
Dans un premier temps, à partir d’une photographie (cf illustration 8) représentant un pont à haubans, il s’agit de schématiser la situation (cf illustration 9), à savoir mettre en évidence les notions de segments, droites, points alignés et droites perpendiculaires. Dans un deuxième temps, la construction d’une figure géométrique est à faire dans l’environnement papier-crayon à partir du schéma, en utilisant les instruments usuels de tracé et de mesure. Enfin, dans un troisième temps, il convient de reproduire la même figure (cf illustration 10) dans l’environnement Tracenpoche.
Choix de conception
Il s’agit chronologiquement de la première situation parmi cinq. L’intégration du logiciel Tracenpoche est récente : les élèves ont découvert celui-ci avec le professeur au cours des séances d’initiation. Il n’était pas prévu que le chercheur soit présent. Dans cette situation 1, la tâche de reproduction proposée aux élèves est d’abord une tâche dans l’environnement papier-crayon puis dans l’environnement Tracenpoche. Comme nous l’avons évoqué précédemment, le mode d’action recherché est donc un mode d’entrelacement. Les connaissances visées sont d’abord des connaissances instrumentales en prenant appui sur des connaissances mathématiques issues de l’environnement papier-crayon. Par exemple, lorsque le pont est représenté par un segment, sur le schéma à main levée ou sur la figure dans l’environnement papier-crayon, l’élève doit tracer un segment avec le bouton « segment »
![]() . Autrement dit, la représentation du « pont » permet d’utiliser les boutons de dessin, c’est-à-dire un mode d’intégration d’initiation instrumentale. Par ailleurs, la connaissance instrumentale du déplacement est présentée : le déplacement de tous les points déplaçables permet de valider une construction. Il est présenté comme le vent contre lequel le pont doit résister. Cette image est provisoire et permet d’introduire ce nouveau mode de validation, propre à l’environnement Tracenpoche. Les connaissances mathématiques sont également en lien étroite avec les connaissances instrumentales. Le « point sur »
. Autrement dit, la représentation du « pont » permet d’utiliser les boutons de dessin, c’est-à-dire un mode d’intégration d’initiation instrumentale. Par ailleurs, la connaissance instrumentale du déplacement est présentée : le déplacement de tous les points déplaçables permet de valider une construction. Il est présenté comme le vent contre lequel le pont doit résister. Cette image est provisoire et permet d’introduire ce nouveau mode de validation, propre à l’environnement Tracenpoche. Les connaissances mathématiques sont également en lien étroite avec les connaissances instrumentales. Le « point sur »
![]() est lié à l’alignement des points. Le bouton « perpendiculaire »
est lié à l’alignement des points. Le bouton « perpendiculaire »
![]() permet d’expliciter la relation ternaire « perpendiculaire + à ? + passant par ? ». En cycle 3, cette notion est connue des élèves, mais elle est souvent implicite et l’équerre permet de tracer la perpendiculaire sans avoir à expliquer ce qui est fait. De ce point de vue, la situation du pont devrait permettre d’établir des conditions favorables pour un renforcement des compétences instrumentales, c’est-à-dire un mode de « renforcement instrumental » du logiciel. La notion de perpendiculaire est connue dans l’environnement papier-crayon, nous proposons une tâche de construction/reproduction dans l’environnement Tracenpoche qui soit problématique, établissant une imbrication des tâches anciennes et nouvelles de sorte à établir une relation de « juste distance ». Nous avons également choisi de faire tracer plusieurs segments pour familiariser les élèves sur des connaissances instrumentales, de type « sélectionner puis valider ».
permet d’expliciter la relation ternaire « perpendiculaire + à ? + passant par ? ». En cycle 3, cette notion est connue des élèves, mais elle est souvent implicite et l’équerre permet de tracer la perpendiculaire sans avoir à expliquer ce qui est fait. De ce point de vue, la situation du pont devrait permettre d’établir des conditions favorables pour un renforcement des compétences instrumentales, c’est-à-dire un mode de « renforcement instrumental » du logiciel. La notion de perpendiculaire est connue dans l’environnement papier-crayon, nous proposons une tâche de construction/reproduction dans l’environnement Tracenpoche qui soit problématique, établissant une imbrication des tâches anciennes et nouvelles de sorte à établir une relation de « juste distance ». Nous avons également choisi de faire tracer plusieurs segments pour familiariser les élèves sur des connaissances instrumentales, de type « sélectionner puis valider ».
4.3 - Exemple : la situation 2
Description
Dans un premier temps, deux rectangles différents sont à compléter, d’abord dans l’environnement papier-crayon puis dans l’environnement Tracenpoche (cf illustrations 11 et 12). Le choix des instruments de tracé est fixé par le professeur, seules la règle non graduée et l’équerre sont autorisées.
Dans un deuxième temps, à partir de deux photographies (cf illustrations 13 et 14), qui représentent le pont du Gard, il convient de schématiser une arche : le but est de mettre en évidence un demi-cercle et un rectangle, dont une longueur est le diamètre du demi-cercle. Enfin, dans un troisième temps, il convient de construire cette figure dans l’environnement Tracenpoche (cf illustration 15).
Choix de conception
Le rectangle est un quadrilatère plutôt connu des élèves : dès le CE2, ils ont construit, reconnu un rectangle avec la règle et l’équerre. Nous faisons le choix d’introduire de nouvelles connaissances instrumentales sur des connaissances mathématiques anciennes. Il s’agit d’établir une juste distance entre l’ancien et le nouveau. Par ailleurs, les techniques dans l’environnement papier-crayon consistent à prendre l’équerre pour tracer les angles droits, sans nécessairement nommer ce qui est fait. Notre intention est de faire construire les perpendiculaires dans l’environnement Tracenpoche de sorte que les élèves aient à choisir le bouton « perpendiculaire », puis à sélectionner et à valider la direction et un point. Dans la première situation, ils ont déjà travaillé cette connaissance instrumentale. Il s’agit donc d’un réinvestissement dans une situation mathématique nouvelle (un rectangle commencé). Pour donner à voir cette évolution, nous alternons l’environnement papier-crayon et l’environnement Tracenpoche (mode d’entrelacement). Comme précédemment, le choix de prendre une photographie, ici le pont du Gard, tient aux habitudes de travail dans les classes. Les élèves ont appris à modéliser la situation. Cependant, nous avons proposé une modélisation qui puisse être réalisée dans l’environnement Tracenpoche sans introduire de nouveau bouton tel que l’arc de cercle (mode juste distance). Ainsi, nous avons proposé une manière de faire aux enseignants, un rectangle et un cercle dont un diamètre est un côté du rectangle. Les boutons pour tracer un cercle sont nouveaux (initiation instrumentale). Les élèves tracent pour la première fois un rectangle, sans aide dans l’environnement Tracenpoche (nouveau), mais ils ont terminé deux rectangles commencés. Ils peuvent s’y référer (mode juste distance). Les élèves ont à utiliser le bouton « rendre invisible »
![]() (mode initiation instrumentale). Cette connaissance instrumentale n’a pas de lien avec des connaissances mathématiques.
(mode initiation instrumentale). Cette connaissance instrumentale n’a pas de lien avec des connaissances mathématiques.
5 - Éléments théoriques pour l’analyse des situations en classe
5.1 - Le modèle du jeu
Les situations étant construites, il ne restait qu’à les expérimenter en classe. Nous les avons proposées à trois professeurs de cycle 3. Pour analyser la mise en œuvre en classe, nous avons modélisé l’action sous forme de jeu (Sensevy, 2011). Le premier niveau de jeu, le jeu didactique, modélise l’action dans l’institution de la classe. Le professeur est soumis à un paradoxe : il sait, pourtant il doit faire preuve de réticence pour permettre à l’élève de faire sienne l’expérience du savoir. Cependant, le professeur agit de manière à accompagner l’élève. Ce « faire faire » est modélisé sous forme d’un deuxième niveau de jeu, le jeu d’apprentissage. Les éléments sur lesquels peuvent s’appuyer le professeur et les élèves font partie du contrat dans le modèle du jeu. Les éléments qui nourrissent l’action ou qui permettent de décrire le problème sont plutôt du côté du milieu didactique.
Dans la classe, l’introduction d’un logiciel de géométrie dynamique conduit le professeur et les élèves à s’appuyer sur ce nouvel outil. Les rétroactions du logiciel doivent être interprétées par l’élève pour produire des stratégies, qu’il soit entre pairs ou avec le professeur. La question qui nous intéresse est de voir comment ces stratégies conduisent l’élève à voir le dessin comme une figure.
C’est ce niveau de jeu d’apprentissage que nous allons développer dans la suite de l’article. Cette modélisation va nous permettre de décrire et d’analyser l’action conjointe du professeur et des élèves lorsqu’ils sont dans l’environnement dynamique.
5.2 - Un exemple :
Dans notre thèse (Athias, 2014), nous avons présenté de nombreux exemples. Ici, nous proposons un moment de la situation 2. Les élèves sont dans la salle informatique. Le professeur a tracé au tableau une figure, un rectangle dont un côté est diamètre d’un cercle. Nous nous intéressons à deux élèves.
L’enjeu est de faire reproduire dans l’environnement Tracenpoche une figure (cf illustration 15) tracée au tableau du point de vue de deux élèves Guillaume et Yann.
Les élèves savent qu’ils ont à reproduire cette figure. Ils ont l’habitude d’utiliser les informations données par le professeur. Ainsi, par exemple, ils ont collectivement mis en évidence les angles droits, le cercle. Ils savent maintenant utiliser les boutons du logiciel. Ils savent qu’ils doivent déplacer pour valider la construction. Du point de vue du modèle, ces éléments sont plutôt du contrat. Les élèves voient à l’écran les effets des sélections et validations successives. Les effets de leurs actions à l’écran permettent aux élèves de se rendre compte des choix qu’ils ont faits. Les effets du déplacement des points modifient la construction à l’écran et doivent permettre à l’élève de valider ou non la construction. Du point de vue du modèle, ces éléments sont plutôt du côté du milieu.
a Description
étape 1 : tracer le cercle de diamètre [AB]
Yann sélectionne le bouton « cercle de diamètre donné »
![]() , il place un point A puis un point B (cf illustration 16). Le cercle étant tracé, il trace le segment [AB]. Puis il déplace le cercle, le point A et il conclut que le cercle est fait (Y : « J’ai déjà fait ça. J’ai déjà fait le cercle avec le diamètre ») (cf illustration 17).
, il place un point A puis un point B (cf illustration 16). Le cercle étant tracé, il trace le segment [AB]. Puis il déplace le cercle, le point A et il conclut que le cercle est fait (Y : « J’ai déjà fait ça. J’ai déjà fait le cercle avec le diamètre ») (cf illustration 17).
étape 2 : tracer les droites perpendiculaires à (AB) passant respectivement par A et B
Yann explique qu’il veut faire un angle droit (Y : « Il faut que ça fasse un angle droit, mais faut trouver »). Par conséquent, il fait défiler tous les menus. Lorsqu’il déroule le deuxième menu (le menu dans lequel il y a les boutons « parallèle », « perpendiculaire », « médiatrice »...) et l’enlève, Guillaume lui demande d’ouvrir à nouveau ce menu (G : « Là, là »). Il lit les bandeaux jaunes et écarte le bouton « médiatrice » (Y : « Construire une médiatrice, c’est pas ça »). Puis, Yann sélectionne le bouton « perpendiculaire », sans être sûr du résultat (G : « Vas-y, vas-y, essaie »). Il sélectionne et valide successivement le point A, puis le segment [AB] [3]. Le résultat obtenu correspond à leurs attentes (G : « Ouais »). Il trace alors la deuxième perpendiculaire sans aucune hésitation [4].
étape 3 : les élèves tracent la perpendiculaire à (d1) passant par un point C
Yann propose alors de tracer un nouveau segment (Y : « Oui mais là comment on va tracer un segment là-dessus »). Il suit avec la souris le mouvement que nous avons représenté par un trait horizontal (cf illustration 18).
D’un côté, Guillaume propose de tracer un segment, qui sera nécessairement perpendiculaire (G : « Tu mets un segment comme ça. Il va être forcément perpendiculaire »). D’un autre côté, Yann montre qu’il faut choisir le bouton « perpendiculaire » et le fait (Y : « Non, c’est là-dedans »). Il trace ainsi la droite [5], perpendiculaire à (d1) passant par C, proposé par le logiciel par un simple clic [6]. Le clic impulsé par l’élève est validé au moment où le point semble être sur (d2) (cf illustration 19).
étape 4 : les élèves analysent l’erreur
NDLR : pour plus de facilité pour le lecteur, nous modifions les figures élèves dans ce qui suit en renommant (perpAsAB) en (d1), (perpBsAB) en (d2) et (perpCperpAsAB) en (d3).
Le professeur, qui se trouve là par hasard, intervient sur la nécessité de déplacer (P : « Il faut bouger pour voir si ça reste accroché »). Les élèves déplacent le point C, qui ne reste pas en tant que point d’intersection des droites (d2) et (d3) (cf illustration 20). Yann reconnaît que la construction est fausse (Y : « Ah non. Le C »). Le professeur confirme (P : « Ah non, le C, ça ne va pas »). Puis le professeur s’en va. Les deux élèves effacent alors la droite qu’ils viennent de tracer, ils déplacent le point B. La figure intermédiaire est juste. Ils en concluent que c’est le point C qui ne convient pas (cf illustration 21) (Y : « Par contre, là, ça reste bien accroché. Alors c’est le point C qui est faux »).
| Vous pouvez faire l’expérience élève et manipuler le point C. |
| Retour à l’étape précédente, validation de cette dernière. Vous pouvez faire l’expérience élève et manipuler le point A ou B. |
étape 5 : les élèves proposent une construction
Après quelques essais infructueux, les élèves recommencent de la même manière, le tracé de la perpendiculaire . Yann explique que c’est la construction fausse faite précédemment (Y : « Tu vois c’est comme tout à l’heure »). Puis ils déplacent le point C (cf illustration 22). Guillaume a alors l’idée de laisser la construction et de placer des points (G : « Je sais, vas-y, fais-là. Va dans les points »). Yann place les points D et E respectivement à l’intersection de (d1) et de (d3) et à l’intersection de (d2) et de (d3) (cf illustration 23).
| vous pouvez déplacer le segment [AB] pour obtenir l’illustration 24 |
Guillaume ne comprend pas ce qu’a fait Yann (G : « Qu’est-ce que tu as fait ? »), mais ce dernier ne sait pas expliquer (Y : « Je ne sais pas »). Puis il déplace le segment [AB] (cf illustration 24) et conclut qu’ils ont réussi. Ils appellent le professeur pour lui faire valider la construction, même s’ils ont un point inutile (Y : « Maître, là, ça marche mais on a un point qui ne sert à rien »).
étape 6 : le professeur valide la construction
Les élèves appellent le professeur puisqu’ils sont parvenus à tracer un rectangle, qui résiste au déplacement. Ils expliquent qu’ils ont un point C parasite (Y : « Maître, nous on a un point qui sert à rien. Le point C il se balade sur la ligne. Mais ceux-là, ça va »). Le professeur valide la construction, puisqu’il leur demande d’enlever les traits de construction.
b Analyse
Dans un premier temps, nous allons montrer l’usage d’un logiciel de géométrie dynamique concernant le bouton « perpendiculaire » par les deux élèves et les spécificités de ce logiciel. Ces derniers savent qu’il faut tracer un angle droit : la connaissance mathématique sous-jacente consiste à tracer trois angles droits pour obtenir un rectangle. Notons qu’à aucun moment, les élèves n’en parlent. Dans l’environnement papier-crayon, tracer un angle droit et tracer deux droites perpendiculaires sont synonymes et nécessitent l’usage de l’équerre (dans le modèle, ces éléments sont plutôt du côté du contrat). Dans l’environnement Tracenpoche, tracer deux droites perpendiculaires avec le bouton « perpendiculaire » est la seule manière de faire. Pourtant, à ce moment-là, pour les élèves, l’équivalence entre ces deux connaissances mathématiques n’est pas disponible, représentant ainsi un empêchement de poursuivre la construction. Les élèves cherchent donc comment tracer un angle droit dans l’environnement Tracenpoche. Ils ont donc un problème à résoudre (dans le modèle, ces éléments sont plutôt du côté du milieu). Pour tenter de le résoudre, les élèves vont dérouler tous les menus. En particulier, ils déroulent les menus du troisième bouton.

Les boutons « perpendiculaire » et « médiatrice » vont permettre aux élèves de faire le lien entre angle droit et droite perpendiculaire. Autrement dit, l’équivalence mathématique devient disponible, à partir des icônes proposées dans les menus du logiciel. Lorsque les élèves choisissent le bouton « perpendiculaire », ils lisent le bandeau jaune « construire une droite passant par un point et perpendiculaire à une droite », aide proposée par l’environnement Tracenpoche. Yann semble convaincu d’être sur le bouton attendu (« T’es sûr que c’est pas ça ? »), Guillaume est plutôt dans une autre stratégie d’essai-erreur (« Vas-y, vas-y, essaie »). Nous savons que la facilité de construction dans l’environnement Tracenpoche peut induire des stratégies d’essai-erreur jusqu’à l’obtention de la construction attendue. En suivant les indications du bandeau jaune, Yann sélectionne successivement le point A, puis le segment [AB]. Concernant la sélection du point A, Yann utilise probablement ses connaissances de l’environnement papier-crayon, pour tracer un angle droit en A, il aurait placé son équerre en A . Concernant le segment [AB], Yann a un moment d’hésitation. Il déplace la souris et le segment [AB] devient rouge, en tant que candidat possible à sélectionner. C’est le seul candidat possible, aucune autre direction n’est disponible. Nous pouvons dire que le logiciel produit un genre d’effet Topaze. Puis, la droite que les élèves obtiennent à l’écran est exactement ce qu’ils voulaient obtenir. Nous pouvons penser que les élèves valident leur construction dans la mesure où le logiciel construit la droite en codant la construction avec l’angle droit (cf illustration 25). Yann trace la deuxième perpendiculaire (d2) sans lire les bandeaux jaunes.
Dans un deuxième temps, nous allons établir un lien potentiel entre l’environnement papier-crayon et l’environnement Tracenpoche. Yann montre d’abord avec le curseur ce que sera la droite (d3) (cf illustration 18). Il anticipe le résultat. Il sait également qu’il doit tracer une perpendiculaire. Il sélectionne le bouton « perpendiculaire », la droite (d1). À l’écran, apparaît donc la droite orange, qui montre ce qu’avait anticipé Yann. Autrement dit, la représentation graphique à l’écran ne peut que valider la méthode de Yann.
Or, lorsque le point C, placé de manière perceptive sur la droite (d2), s’affiche à l’écran, aucun signe ne lui permet de se rendre compte que le point C est un point libre (cf illustration 27).
| Faites l’expérience de Yann. Manipulez la figure. |
Ce n’est qu’au moment du déplacement des points qu’ils peuvent le faire. Yann est capable de dire que la construction proposée ne correspond pas à ce qu’il attendait [7] (Y : « Ah, non, le C »). Notons alors comment ils élaborent une nouvelle stratégie. Ils repèrent que la construction est fausse lorsqu’ils ont tracé la droite (d3) et le point C (étape n). Ils effacent le point C et la droite (d3) et déplacent le point B. Ils notent alors que la construction est juste (étape n-1). Ils en concluent que c’est le point C qui est faux (passage entre l’étape n-1 et n). Autrement dit, ils mettent en œuvre le raisonnement suivant : si la construction est juste à l’étape n-1 et qu’elle est fausse à l’étape n, c’est que le passage de l’étape n-1 à n est faux. Les rétroactions du logiciel leur permettent de voir uniquement que le point C est « faux ». Les deux élèves ne comprennent pas en quoi ce point C est faux. Les élèves rencontrent donc un problème, mais ils l’interprètent de manière erronée. Du point de vue du modèle, le milieu est résistant et ne permet pas aux élèves de se rendre compte du problème réel.
Dans un troisième temps, nous allons montrer l’ingéniosité des élèves. La construction a été déclarée fausse par les élèves puis confirmée par le professeur. Cependant les élèves vont prendre appui sur cette même construction pour tracer un rectangle en tant que quadrilatère ayant trois angles droits. Les deux premiers sommets sont A et B, les élèves nomment les deux autres D et E. Le rectangle ABED est construit en tenant compte des propriétés mathématiques - trois angles droits - , il résiste donc au déplacement, la construction est donc validée par les élèves. Les différentes représentations graphiques donnent à voir des rectangles. Du point de vue du modèle, le milieu renvoie un signe, interprété comme une validation par les élèves. Or cette validation peut être discutée : une connaissance instrumentale masque une propriété géométrique. À notre niveau, c’est précisément cette absence d’explicitation qui nous interroge en géométrie au cycle 3.
Enfin, dans un quatrième temps, nous nous interrogeons sur le rôle du professeur. Les élèves demandent une validation par le professeur. Ce dernier ne prend pas appui sur ce point C « inutile ». Il ne saisit pas l’occasion de faire préciser aux élèves ce qu’ils ont construit. Il reste en retrait au moment de la validation. Est-ce qu’il est aisé pour lui d’interpréter la construction proposée ? Les élèves travaillent dans le même but, à savoir construire une figure, qui conserve ses propriétés au cours du déplacement. Ils y sont parvenus. Le professeur, absent aux moments des échanges, sera appelé uniquement pour validation. Il semblerait que la complexité de la démarche de l’élève n’ait pas été saisie par l’enseignant.
6 - Conclusion-discussion
Les éléments du cadre théorique nous ont permis de décrire et d’analyser le travail de deux élèves dans l’environnement Tracenpoche. À travers cet exemple, nous illustrons comment des propriétés mathématiques connues peuvent être retravaillées dans l’environnement dynamique, afin d’être approfondies. Nous avons montré comment les élèves prennent appui sur les fonctionnalités de ce logiciel, tels que les bandeaux jaunes. Ils se rendent capables de tracer une droite perpendiculaire, en précisant ses caractéristiques : pour cela, ils sélectionnent et valident un point et une direction. Ils établissent un lien entre angle droit et perpendiculaires. Dans le même temps, nous voyons également des limites du travail en autonomie avec le logiciel : une même assertion peut être jugée vraie ou fausse selon le moment. Notons que les élèves ont effectivement tracé un rectangle dans la mesure où il a trois angles droits. Mais le processus de construction ne semble pas compris par les élèves, ni par le professeur. À ce moment, nous pourrions envisager un travail sur ce que les élèves ont effectivement tracé et établir un lien entre ce que propose le logiciel (la droite orange et le point C —cf illustration 26—) et ce que l’on fait dans l’environnement papier-crayon (on place l’équerre sur la droite (d2) et c’est la position de l’équerre qui permet de déterminer le lieu de C et de D). Les fonctionnalités du logiciel deviennent alors le révélateur de propriétés implicites dans l’environnement papier-crayon. En ce sens, il est intéressant que le logiciel place un point C libre sans proposer de placer le point C sur la droite. Par contre, cette caractéristique empêche ici les élèves et le professeur de produire un rectangle ABCD, avec le point C convenu [8]. Faut-il le regretter ?
Bibliographie
- Assude, T., (2007), Modes et degré d’intégration de Cabri dans des classes du primaire. In F.Ruhal et F. Conne (Eds). Environnements informatiques, enjeux pour l’enseignement des mathématiques (pp. 119-134). Bruxelles : De Boeck.
- Athias, F. (2014). La géométrie dynamique comme moyen de changement curriculaire, thèse de doctorat, Université Aix-Marseille.
- Laborde, C. et Capponi, B., (1994), Cabri géomètre constituant d’un milieu pour l’apprentissage de la notion de figure géométrique, Recherches en Didactique des Mathématiques, 14-1/2, pp. 165-210.
- Sensevy, G. (2011). Le sens du savoir. Éléments pour une théorie de l’action conjointe en didactique. De Boeck.