Expériences, modèles, simulations
Dans cet article, je voudrais présenter deux expériences menées dans des contextes différents ; la première a été menée dans le cadre d’une classe européenne regroupant des élèves de seconde, première S et terminale S. La seconde a été réalisée dans une classe de terminale S et s’appuie sur une situation mathématique proposée par Trouche (1998). Je montre ici un aspect lié à l’investigation par des élèves d’une petite partie des mathématiques ayant pour déclencheur une situation problématisée.
Dans une première partie j’essaierais de montrer la différence entre la recherche d’un problème et une situation d’investigation en mathématiques. Dans un second temps nous décrirons le travail réalisé dans les classes et essaierons de dégager les éléments importants permettant de mener à bien de telles expériences.
Vous avez dit : investigation ?
Le terme « démarche d’investigation » est plutôt utilisé dans les enseignements des sciences expérimentales. Les expérimentations visant à rénover l’enseignement scientifique au lycée s’inscrivent dans un contexte international de désaffection des filières scientifiques (OCDE 2006) et visent à proposer une modification de l’enseignement des sciences en impliquant les élèves dans une réflexion à propos de problèmes scientifiques cruciaux. Les élèves sont ainsi conduits à mener leurs propres investigations de manière autonome. Une des difficultés importantes est la question de l’élaboration de situations, suffisamment riches pour permettre une réelle investigation, et suffisamment accessibles pour pouvoir être abordées par les élèves en autonomie. Il est clair que mettre les élèves en autonomie nécessite une mise en situation construite par l’enseignant, permettant de confier la responsabilité de tâches aux élèves. Dans ce contexte, les problèmes longs (Aldon et Tisseron, 1998, Arsac et Mante, 2007) articulent le programme de mathématiques d’une classe et la recherche d’un problème, les notions enseignées en classe étant autant d’outils nouveaux pour explorer, un peu plus le problème, explorer, investiguer une petite partie des mathématiques (Aldon, 1995, 2007, Trouche, 1998). La dimension expérimentale des mathématiques permet ainsi de faire entrer les élèves dans des démarches actives vis à vis de leurs apprentissages. Mais, tout comme dans les sciences expérimentales, l’expérience n’a de sens que lorsqu’elle débouche sur des questions sur les résultats observés :
« Ce qui caractérise la dimension expérimentale en mathématiques, c’est le va-et-vient entre un travail avec les objets que l’on essaye de définir et de délimiter et l’élaboration et/ou la mise à l’épreuve d’une théorie, le plus souvent locale, visant à rendre compte des propriétés de ces objets . »
(Durand-Guerrier in Aldon et al., 2010, à paraître)
L’organisation du « milieu » au sens de Brousseau (2004) par le professeur vise à faciliter des rétroactions permettant aux élèves de confronter les résultats obtenus par des actions sur les objets et le traitement mathématique général. Une hypothèse très importante de la théorie des situations didactiques est que le sujet apprend en s’adaptant à un milieu qui produit des contradictions. Les élèves agissent sur le milieu et le milieu renvoie des renseignements, des rétroactions qui doivent permettre aux élèves de construire les connaissances visées dans une situation construite. En ce sens, les calculatrices, les logiciels de représentation ou de géométrie sont des éléments importants du milieu des élèves et permettent de mettre en place des expériences qui nécessitent ensuite une réflexion sur les observations :
« Une science expérimentale ne commence pas avec l’observation mais avec l’interrogation sur l’observation » (Treiner, 2007)
Ce sont ces réflexions que je voudrais illustrer dans les paragraphes qui suivent en m’appuyant sur des travaux menés dans deux contextes bien différents : d’une part un travail en classe européenne et d’autre part dans une classe de Terminale S.
De la boule à la terre
Ce travail s’est déroulé dans une classe d’un lycée de la banlieue lyonnaise, à Vénissieux. Les élèves impliqués suivent les cours des classes européennes et viennent de Seconde, Première S et Terminale S. Une des difficultés d’enseignement était bien sûr la gestion de trois niveaux de classe bien différents les uns des autres. De façon à gérer cette hétérogénéité, le travail proposé reposait sur des concepts mathématiques qu’il était possible d’aborder dès la classe de seconde, mais suffisamment résistants pour pouvoir alimenter une réflexion en classe de première et de terminale.
Ainsi, dans cette classe européenne, un grand nombre des sujets abordés mettaient les élèves en action dans des démarches leur permettant de poser des problèmes puis d’explorer des petites parties des mathématiques donnant des clefs de compréhension du phénomène observé. Par exemple,
– Mesure des dimensions de la cour de récréation en restant à l’intérieur de la salle de classe.
– La planche de Galton : histoire, théorie et simulation.
– Comment multiplier deux nombres ?
– Résolution d’une équation du troisième degré : vers les nombres complexes, histoire, petites histoires, théorie.
– Etc.
Bien entendu, dans chacun de ces thèmes, les rôles des élèves des différentes classes variaient en fonction de leurs connaissances et des programmes de mathématiques, mais tous s’ancraient sur l’histoire des mathématiques et se prolongeaient par des simulations sur ordinateur ou des expériences concrètes. Nous nous intéresserons dans cet article à un travail spécifique réalisé dans cette classe et dont l’objet était la mesure du rayon de la Terre. Nous avons profité du fait que les élèves correspondaient avec des élèves polonais d’une école d’une petite ville de Haute Silésie (Łaziska [1]) pour poser la question de la distance entre les deux villes à la surface de la terre.
Petit à petit, les questions ont surgi du travail collectif des élèves : comment repérer les villes sur la terre, et en modélisant le questionnement, comment se repérer sur la sphère ? Connaissant les latitudes et longitudes des deux villes, comment calculer la distance entre les deux villes ? Quel est le plus court chemin entre deux points d’une sphère ? Quel est le lien avec l’expérience d’Eratosthène de la mesure du rayon de la terre connu des élèves ?
Le cours se déroulant en anglais, j’ai utilisé des enregistrements audio (http://www.uh.edu/engines/epi1457.htm) et des textes provenant du site « Engines of our ingenuity » (http://www.uh.edu/engines/) de l’Université de Houston en Californie. Ces documents expliquent brièvement la démarche et la méthode d’Eratosthène et le travail confié aux élèves de seconde fut alors de comprendre et de traduire
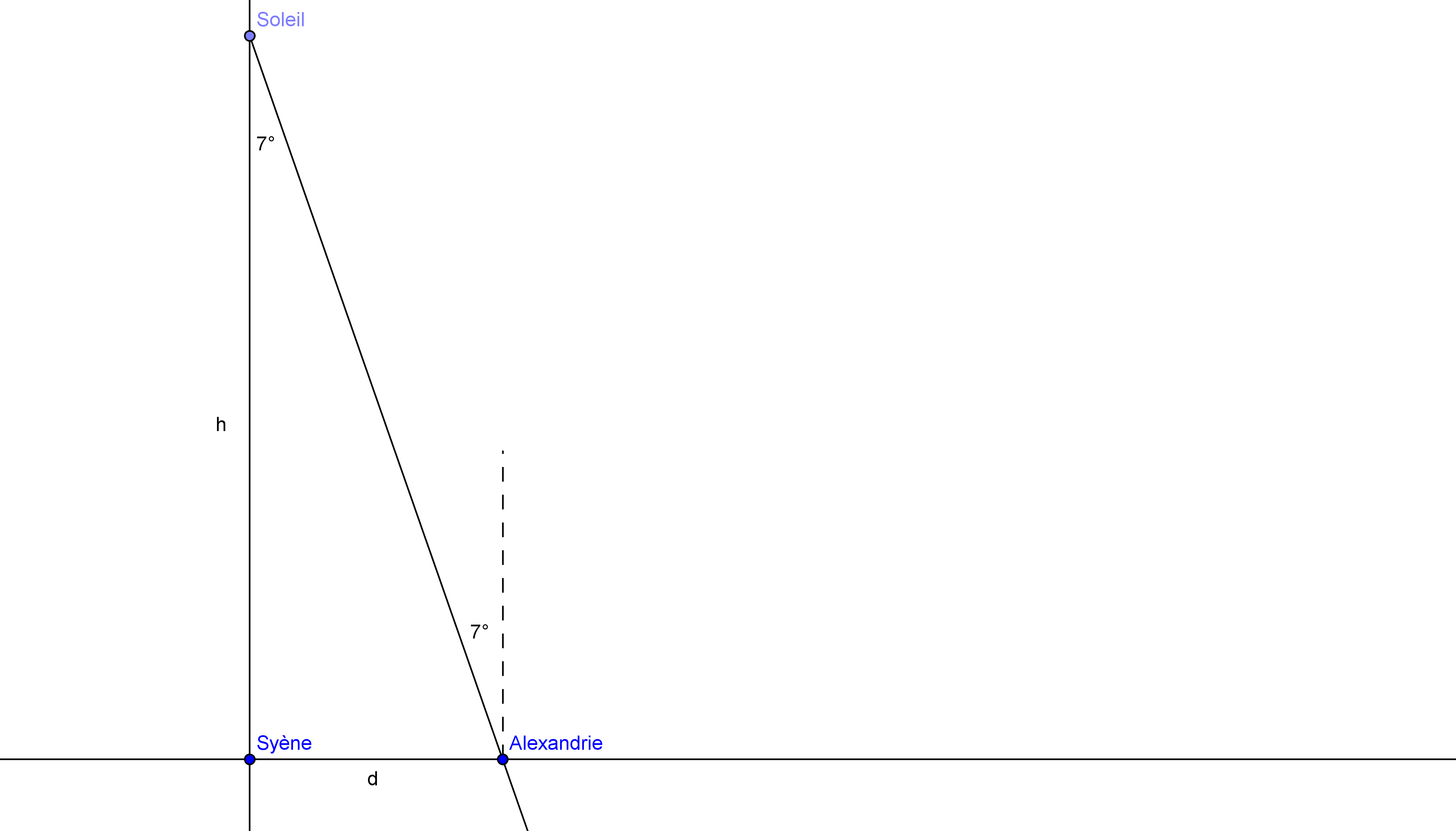
les textes dans un langage mathématique « opérationnel » en ce sens qu’il leurs permettent de mettre en place l’expérience. Un travail spécifique sur l’histoire des mathématiques, (replacer Alexandrie dans le contexte scientifique du troisième siècle avant Jésus-Christ), mais aussi des rappels sur les cartes et leur histoire, sur le repérage d’un point sur la terre dans un système de coordonnées cartésiennes ou géographiques et le passage de l’un à l’autre, furent des éléments importants de l’investigation que les élèves de seconde firent dans cette première partie ; en première, les élèves se sont penchés sur la question des hypothèses fondant cette méthode : le soleil est suffisamment loin de la Terre pour que l’on puisse considérer les rayons comme parallèles et la méthode d’Eratosthène permet le calcul du rayon de la Terre, ou bien, le soleil est proche de la Terre comme Anaxagore [2] le pensait et l’expérience montre que la hauteur du soleil se calcule comme le rapport de la distance entre les deux villes et la tangente de l’angle, soit :
$ {h= { \frac{d} {\textrm{tan} \left( α \right) } } = { \frac{\textrm{800}} {\textrm{tan} \left( 7° \right) } } \approx \textrm{6515} \textrm{km}} {}$ (Aldon, 2008)
Expérience en laboratoire
En s’appuyant sur ces documents et sur leurs connaissances (la méthode d’Eratosthène avait été vue de façon théorique en physique) les élèves de seconde ont mis au point une expérience pour « tester » la méthode en mesurant le rayon d’une boule (en fait, un abat-jour d’un des lampadaires du lycée resté en réserve dans les caves du lycée).
Le matériel : un rétroprojecteur, une boule dont il s’agit de déterminer le rayon
deux bâtonnets collés sur la sphère « verticalement »
Pour réaliser cette expérience, il a fallu un rétroprojecteur, une boule, deux bâtonnets, un peu de colle et une règle souple permettant donc de mesurer une distance sur la surface de la sphère.
Voir ci-dessous un film tourné par les élèves.
Par ailleurs, les élèves de première et terminale se sont attelés à une simulation des positions respectives des deux villes sur la sphère terrestre et de convertir les coordonnées sphériques et cartésiennes.
Voici une copie d’écran d’une figure créée par les élèves avec Geospace :

Pour récupérer la figure Geospace correspondante
Le travail avec Geospace m’a également permis de faire construire une carte par projection plane en partant des contours de la France repérée par ses coordonnées géographiques.
Voici une copie d’écran d’une figure créée par les élèves :

Pour récupérer la figure Geospace correspondante
Les élèves de Terminale ont eu, quant à eux à résoudre le problème de la détermination de l’heure à laquelle l’expérience si elle avait lieu entre les deux villes devrait être réalisée ; en effet, contrairement à Alexandrie et Syène situées sur un même méridien, Vénissieux et Laziska sont à des longitudes différentes. « A quelles heures le soleil est-il aligné avec le grand cercle passant par ces deux villes ? » a été la question que les élèves de terminale ont résolue.
Ce travail d’investigation avait par ailleurs un but pour les élèves puisqu’ils ont eu en charge d’expliquer à leurs homologues polonais les résultats auxquels ils étaient arrivés et par conséquent de synthétiser leurs recherches.
Do not just pay attention to the words ; Instead pay attention to meanings behind the words. But, do not just pay attention to meanings behind the words ; Instead pay attention to your deep experience of those meanings.
Tenzin Gyatso, The Fourteenth Dalai Lama
La trajectoire de l’avion
Le deuxième exemple pour illustrer un travail d’investigation en mathématiques est un travail effectué en classe de terminale S et ayant comme support le problème de la trajectoire de l’avion (Trouche, 1998, Aldon, 1999). Les élèves de cette classe avaient à leur disposition au moment de cette expérience une calculatrice TI-92.
| Enoncé du problème
Le dessin est une modélisation des contraintes s’exerçant sur la trajectoire d’un avion : Il décolle en O, origine du repère, doit passer au dessus d’un relief qui culmine en B, puis passer au dessus du plateau [DE], mais sous la masse nuageuse (IJKL), et enfin atterrir sur une piste qui commence en F, et de longueur infinie. Le contact avec la piste, pour qu’il soit le plus doux possible doit se faire « à l’infini ». |
| 1) Déterminer une fonction dérivable sur [0,$+\infty$[, dont la représentation graphique satisfasse à toutes ces contraintes. |
| 2) Dans un deuxième temps, on veut optimiser le trajet. L’idée est que l’avion « monte le moins possible ». Cela peut se comprendre d’au moins deux façons : l’avion transporte des passagers et le pilote s’arrange pour que, sur le trajet, la pente maximale de l’avion (en valeur absolue) soit la plus faible possible. Pour deux fonctions f et g, on considèrera sup(f ’) et sup(g ’). La fonction qui aura le plus petit sup sera réputée la meilleure. l’avion est un avion espion. Il devra donc voler au plus près des reliefs. |
 Les points ont les coordonnées suivantes : O(0,0), A(5,0), B(5,4), C(6,4), D(6,2), E(10,2), F(10,0), I(10,3), J(10,4), K(7,4), L(7,3) |
Il ne s’agit pas ici de relater l’ensemble du travail mené par les élèves de la classe de Terminale S dans le temps, mais plutôt de s’attarder sur le comportement d’un groupe de quatre élèves à un moment donné de leurs recherches. Alors que l’énoncé du problème avait été donné dès le début de l’année, dans le cours de mathématiques, j’ai abordé la fonction exponentielle et, en guise d’exercice, donné aux élèves l’étude de la fonction gaussienne : $x \rightarrow e^{-x^2}$.
Pour ce groupe d’élève, la représentation graphique de la fonction est apparue comme une solution potentielle au problème de la trajectoire de l’avion, et cet exercice, somme toute banal a été le déclencheur d’une étude approfondie des courbes des fonctions de la forme $e^{-kx^2}$ avec k un nombre réel positif. L’utilisation de la calculatrice graphique montre rapidement que plus k est petit et plus la courbe est « large » ; et c’est précisément cette notion que les élèves ont défini puis étudié (ci-dessous sont reproduites les définitions et propriétés exposées à la classe lors d’une mise en commun) :
« On appellera largeur de la courbe, la longueur du segment reliant les points de la courbe d’ordonnée 1/2 »
Pour ensuite arriver à la propriété :
« La largeur de la courbe de la fonction $x \rightarrow e^{-kx^2}$ vaut $2 \sqrt{ \frac{ln2}{k}} $ »
et enfin
« la largeur de la courbe est une fonction décroissante de k et est une bijection de [0, $+\infty$[ sur [0,$+\infty$[ »
Chacune des propriétés était accompagnée d’une démonstration et illustrée sur la calculatrice. Le problème initial n’est pas résolu, mais l’étude réalisée montre bien à la fois l’investissement des élèves et les pistes qui peuvent être encore explorées. C’est bien sûr vers ces pistes que les commentaires de cet exposé sont allés et les élèves sont repartis en ayant pour tâche d’explorer les fonctions du type $x \rightarrow e^{-kx^n}$ avec n>=2 et d’autre part, d’ajuster, en jouant avec des constantes additives et multiplicatives la courbe aux contraintes de l’énoncé. Les recherches sont alors relancées et les résultats des uns alimentent les recherches des autres.
Conclusion
Dans ces deux extraits et ces rapides survols du travail des élèves, je voudrais surtout souligner les conditions permettant cette exploration d’un petit bout de mathématiques. On voit bien que les résultats ici obtenus ne sont pas extraordinaires en regard des programmes des classes concernées, mais ce qui est remarquable c’est le fait que les problèmes ont été posés et résolus par des groupes d’élèves dans une démarche autonome. La « dévolution » du problème, c’est à dire les conditions mises en place dans la classe pour que le problème ne soit plus le problème du professeur mais le problème des élèves passe dans les deux cas par le partage d’une culture commune dans la classe de mathématiques dans laquelle la recherche de problèmes joue un rôle prépondérant. Mais aussi par la mise en place d’un milieu suffisamment riche et antagoniste pour que les expériences réalisées renvoient d’elles-mêmes des rétroactions permettant de saisir les objets mathématiques. Ainsi, l’expérience concrète de la mesure du rayon de la boule pouvait être vérifiée, contrôlée (et elle l’a été) par la mesure directe utilisant le périmètre de la boule. De la même façon, la calculatrice dans les études des fonctions gaussiennes apportent des confirmations des conjectures émises tout au long des recherches et permet, plus que d’obtenir des résultats, de mettre en confiance dans la justesse d’une piste suivie.
Les allers-retours entre les expériences, que ce soit sur des objets concrets (l’abat jour des lampadaires du lycée) ou abstraits (les courbes des fonctions gaussiennes), les notions mathématiques sous-jacentes, les simulations effectuées sur machine ou la mise en perspective des modèles mathématiques permettent de construire les connaissances des objets mathématiques en leur donnant successivement des statuts différents d’outils et d’objets.
Bibliographie
Aldon, G., Cahuet, P.-Y., Durand-Guerrier, V., Front, M., Krieger, D., Mizony, M. et Tardy, C. (2010). Expérimenter des problèmes de recherche innovants en mathématiques à l’école . Cédérom, INRP. à paraître.
Aldon, G. (2008) Modéliser, simuler en mathématiques. Cahiers de l’ingénierie éducative , 63-64:76–77.
Aldon, G. (2007) La place des TICE dans une démarche expérimentale en mathématiques , Actes de l’Université d’été de Saint Flour “Expérimentation et démarches d’investigation en Mathématiques”
Aldon, G. (1999) Démarche scientifique et calculatrices symboliques, in Guin, D. Trouche, L. (ed.), Calculatrices symboliques et géométriques dans l’enseignement des mathématiques. Actes du colloque francophone européen de La Grande-Motte. IREM de Montpellier
Aldon G., Tisseron C. (1998) Des situations pour mettre en œuvre une démarche scientifique au lycée , Colloque Recherche et Formation, Actes, IUFM de Grenoble
Aldon, G. (1995) Une voiture à la Derive , Repères IREM, num.21, p. 27-44
Arsac, G. Mante, M. (2007) Les pratiques du problème ouvert, IREM et CRDP de Lyon
Brousseau, G. (2004) Théorie des situations didactiques, La pensée sauvage éditions.
Dias T., Durand-Guerrier V. (2005) Expérimenter pour apprendre en mathématiques , Repères IREM, 60, pp. 61-78
OCDE (2006). Evolution of student interest in science and technology studies , OCDE.
Treiner, J. (2007), Expérimenter en Sciences Physiques : le point de vue d’un théoricien , Actes de l’Université d’été de Saint Flour “Expérimentation et démarches d’investigation en Mathématiques”
Trouche L. (1998), Expérimenter et prouver, faire des mathématiques avec des calculatrices symboliques, 38 variations sur un thème imposé . IREM de Montpellier