Un bon moyen de donner une note qui récompense le travail (et non les compétences ni les connaissances), est de demander en devoir maison, de tracer une courbe sur papier millimétré :

• Comme le soin est noté, il est difficile de copier le corrigé à la va-vite sur Internet en espérant remonter sa moyenne sans effort : le travail est personnel.
• Je dis que si moins de 20 points ont été utilisés pour tracer la courbe, il est peu probable que le soin et la précision soient satisfaisants [5] : le travail n’est pas bâclé par ceux qui ont écouté mon conseil (à moins de désirer une mauvaise note, ça existe).
• Sur ce genre de devoir, les élèves n’osent pas prétendre qu’ils n’ont pas fait le travail parce qu’ils n’ont rien compris.
• En cas de septaine (ça arrive) il reste possible de me faire parvenir le travail, en le scannant (ou le photographiant) puis en envoyant le résultat par Moodle ou autre.

Il a donc été demandé à des étudiants de BTS 1ère année de représenter graphiquement la fonction logarithme, le résultat, après évaluation, étant destiné à aboutir dans le cahier de cours.

Sur calculatrice (on prendra ici comme exemple la Numworks car elle est dotée d’un émulateur en ligne) il est très rapide d’obtenir la représentation graphique de la fonction logarithme :

• aller vers l’application des fonctions puis appuyer sur le bouton OK
• appuyer sur OK une deuxième fois sur « ajouter une fonction »
• ln puis x,n,t et OK pour entrer la fonction
• descendre avec la flèche vers le bas jusqu’à « tracer la fonction » puis OK

Et c’est tout, on a cette courbe en quelques secondes :

Mais ces quelques secondes suffisent-elles pour que l’élève qui a appuyé sur ces boutons, ait le temps de comprendre de ce que c’est qu’une fonction ?

Par contre, la calculatrice peut aider pour tracer une courbe sur papier millimétré, il suffit pour cela d’afficher, en lieu et place de la courbe, le tableau de valeur. Sur Numworks, à la fin de l’étape précédente, il suffit de remonter avec la flèche vers le haut puis aller sur « tableau » avec la flèche vers la droite, pour avoir le tableau de valeur qui raccourcit le placement des points sur le graphique :

Ceci dit, le réglage par défaut n’est pas optimal, comme le montrent certains des exemples ci-après. Mais en montant vers « régler l’intervalle » puis en appuyant sur OK on voit

En modifiant ces réglages, par exemple avec

on a un tableau plus utile :

En ne plaçant que des points à abscisse entière, on peine à obtenir les 20 points demandés :

Cela amène à établir une conjecture sur la limite en 0 :

On dirait (graphiquement) que ln(0)=-2

Après avoir placé une vingtaine de points sur le graphique, on est censé les relier par une courbe. Ce point a parfois été oublié :

En plus, il arrive qu’en essayant de faire passer la courbe par les points, on détecte des erreurs et cela amène à gommer les points erronés (vers la gauche) pour refaire la partie de la courbe concernée :

Mais parfois (par manque d’expérience, surprenant ici puisqu’il s’agit d’une bachelière pro) on essaye quand même de tracer la courbe, quitte à zigzaguer un peu :

Lorsque les unités sont complexes (comme 2cm sur l’axe des x et 4mm sur celui des y) il s’ajoute aux difficultés précédentes, celle d’avoir à résoudre plusieurs fois un problème de proportionnalité. Dans ce cas, on gagne à mettre dans la calculatrice une seconde fonction du type b×f(x/a) où a et b sont les échelles sur les axes, puis afficher la nouvelle table de valeurs obtenue.

Mais ici, les unités étaient 1cm sur chaque axe. Malgré cela, il y a des problèmes pour les garder affines :

Dans son livre la bosse des maths (ISBN 978-2738125248), Stanislas Dehaene évoque une expérience montrant une certaine tendance à placer la graduation 100 au milieu des graduations 10 et 1000, ce qui laisse penser à une perception logarithmique des nombres (grandeurs). Cela donne de l’importance au papier logarithmique (qui n’est pas millimétré) voire au doublement logarithmique.

Des TP sur les diagrammes de Bode ont déjà été donnés, sur papier doublement logarithmique.

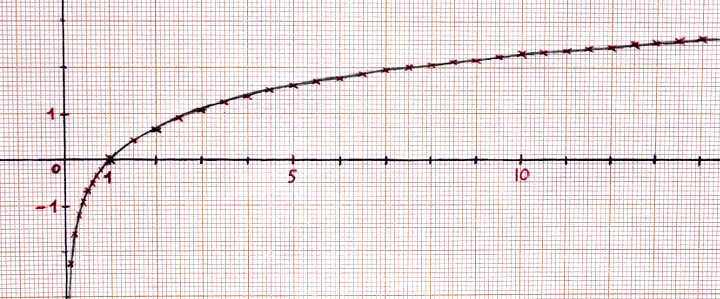
Voici des représentations graphiques conformes à ce qui était attendu :

On gagne en précision lorsque les abscisses sont plus proches dans les zones où la pente est importante. L’idée générale étant de maintenir dans une limite raisonnable la distance euclidienne entre deux points consécutifs sur la courbe. Cette compétence s’acquiert par l’expérience.

On devine presque l’asymptote :

Cependant, les élèves ayant passé le plus de temps sur cette activité sont ceux qui n’en ont pas besoin (ceux qui semblent bien savoir ce qu’est une fonction, ce qu’est une représentation graphique et qui maîtrisent bien les coordonnées et la proportionnalité). A contrario, ceux qui ont le plus besoin de ce genre d’activité ne la font pas du tout.

Le papier millimétré peut aussi servir à introduire la notion d’intégrale. Par exemple l’intégrale de ln(x) entre 1 et e est l’aire coloriée en vert ci-dessous :

Pour estimer l’intégrale en question, il suffit de compter les carrés d’un millimètre de côté qui sont majoritairement coloriés en vert. On en trouve 100.

Mais peut-être est-ce plus rapide de compter les petits carreaux par colonnes ? On trouve

1+2+2+3+4 + 4+5+6+7+7 + 7+8+8+8+9 + 9+10 = 12+29+40+19 = 100

Mais ça, c’est juste la méthode des rectangles : pour chaque rectangle de largeur dx=1mm, on obtient son aire en comptant les millimètres qui entrent dans la hauteur du rectangle, et cette hauteur est facile (et rapide) à lire avec les graduations.

Cela est emblématique du triptyque manipuler→verbaliser→apprendre : Compter des petits carreaux, c’est long, il peut alors être intéressant de s’arrêter un instant pour chercher une technique de comptage plus rapide, et cette technique est typiquement le regroupement des petits carreaux en rectangles verticaux.

Ceci dit, la chronologie serait plutôt manipuler→abstraire→verbaliser car l’idée de compter les carreaux par paquets verticaux se fait d’abord dans l’abstrait avant de pouver la verbaliser.

Aucune primitive de ln(x) n’étant au programme, on peut demander à un logiciel de calcul formel (par exemple KhiCAS sur la calculatrice) d’en calculer une, ou la donner en énoncé, en demandant de vérifier que la dérivée de x×ln(x)-x est égale à ln(x).

Une primitive étant connue, on peut calculer la valeur exacte de l’intégrale : c’est e×ln(e)-e-1×ln(1)+1=e×1-e-1×0+1=e-e-0+1=1.

L’intérêt de calculer les intégrales de cette manière est plus évident pour quelqu’un qui a passé du temps à compter des minuscules carrés en risquant de se tromper : une économie de temps et d’énergie, ça ne se refuse pas !

Les calculatrices (par exemple la Numworks présentée ici) permettent facilement de calculer une intégrale une fois qu’on a représenté graphiquement la fonction, avec coloriage à la clé. Sur Numworks, une fois la fonction représentée graphiquement,

• un appui sur OK fait apparaître ce menu :

• un second appui sur OK pui on défile vers le bas jusqu’à

• un appui sur EXE fait revenir à l’écran du graphique mais avec la demande d’entrer la borne inférieure :

• 1 puis EXE et la calculatrice attend la borne supérieure :

• Comme la Numworks ne dispose pas de touche donnant le nombre e, il faut appuyer sur e^x puis 1. Un dernier appui sur EXE donne l’intégrale et le coloriage :

Mais ça va vite, probablement trop vite pour le temps de l’apprentissage, et ne sollicite pas ce que Papert appelait « la mémoire des muscles »...

En 1903, dans notions de mathématiques (Delagrave), Tannery (voir plus bas la partie sur l’histoire) proposait déjà ce genre d’activité en lycée :

En Seconde, à l’intersection des thèmes données structurées et objets connectés (ici, la robotique) a été proposée l’activité « débranchée [6] » suivante [7] :

Il s’agit là de préparer les élèves à la compréhension de la manière dont un robot perçoit les obstacles (mesure de distance par ultrasons), de rappeler qu’il faut deux coordonnées pour repérer un point et que l’une au moins de ces coordonnées peut être un angle, d’initier à la syntaxe Python et surtout de rappeler la présentation des données en table, ici avec deux colonnes dont la première est créée par le programme Python (rotations imposées au robot pour obtenir les angles) et la seconde obtenue par des mesures (à l’aide du télémètre à ultrasons, similaire à celui des vrais robots que les élèves manipuleront plus tard).

Avec

en créant une liste X pour les angles et une autre liste Y pour les distances, il suffit de faire

pour obtenir le corrigé suivant :

Mais ça c’est pour le prof, pas pour les élèves. Noter qu’avec 36 points à tracer chaque élève disposait de plus d’une minute par point.

Lenteur ou mauvaise volonté, certains semblent avoir plutôt fait semblant de travailler, que travailler vraiment, en une demi-heure ils n’ont produit que ce genre de tentative :

Ces élèves posent problème car ils ralentissent toute la classe. Ce phénomène montre l’intérêt qu’il y a à réduire les effectifs en SNT, même sur des activités débranchées.

Beaucoup d’élèves ont trouvé plus pratique de représenter d’abord tous les angles et seulement après, les longueurs.

Cela révèle en passant la forme du rapporteur :

Mais cette technique ne protège pas des erreurs sur les longueurs :

D’autres élèves, plus méthodiques, ont effectué la construction point par point :

Leurs voisins ont eu, en général, du mal à copier correctement le dessin :

Mais ce qui est bien avec les activités mobilisant le canal kinesthésique, c’est que même copier sur le voisin, est déjà un travail, nécessitant souvent plus d’énergie que le travail attendu !

Si les traits reliant l’origine aux points des murs mesurés, n’étaient pas aussi épais (ou n’étaient pas tracés du tout) le dessin serait parfait :

La meilleure production, où les points construits avec une relativement bonne précision sont reliés :

Ici, la courbe ne passe pas exactement par les points construits, parce que l’hypothèse a été faite qu’il s’agit d’une pièce rectangulaire et a été tracé le profil le plus vraisemblable possible passant près des points :

Et ici, le constat a été fait qu’il y a une certaine symétrie dans les résultats numériques, et cette symétrie a été exploitée pour raccourcir le travail :

On voit là un apport inattendu des tâches répétitives proposées : ce que j’appelle paresse constructive incite à chercher des astuces pour rendre le travail moins répétitif que prévu, ce qui passe par le processus suivant :

• émettre des hypothèses (ici,la symétrie des données)
• les vérifier sur l’ensemble des données pour les confirmer ou infirmer (ici l’hypothèse est confirmée)
• utiliser ce savoir nouvellement acquis pour accélérer l’expérimentation (ou émettre de nouvelles hypothèses etc).

Ne s’agit-il pas là de l’essence d’une activité scientifique ? Il est à remarquer que l’élève qui a produit le dessin ci-dessus n’a aucune vocation scientifique [8]...

Le nomogramme circulaire de Clark a déjà été utilisé pour le cours sur les limites. Cela a révélé que les nomogrammes permettent d’effectuer des opérations de manière kinesthésique [9].

En général, un nomogramme sert à effectuer des calculs portant sur plusieurs variables. Comment peut-on se servir de nomogrammes pour calculer des fonctions (à une seule variable ici) ?

Maurice d’Ocagne, inventeur du concept de nomographie, dessinait ainsi les fonctions, avec deux échelles sur un seul segment :

Comme les rôles des échelles sont interchangeables, on peut utiliser le même nomogramme pour calculer des exponentielles.

Toute fonction monotone sur un intervalle peut être représentée ainsi et ce genre de nomogramme permet donc de calculer des fonctions de répartition comme par exemple celle de la loi normale...

Le segment à double graduation style d’Ocagne de l’onglet précédent, prend peu de place et il est possible d’en placer plusieurs (pour plusieurs fonctions) dans une même annexe à un sujet d’examen (ce qui permettrait alors d’interdire la calculatrice). On mettrait plusieurs segments doublement gradués parallèlement l’un à l’autre, avec le nom de la fonction à côté de chaque segment.

Mais dans les règles à calcul, la graduation des x n’est donnée qu’une seule fois et chaque axe n’est gradué que d’un côté (x ou f(x) selon le cas). Cela revient à séparer les deux graduations du segment précédent :

Comme les segments gradués sont parallèles, une équerre est nécessaire pour utiliser ce nomogramme. Sur les règles à calcul, ce sont des guides transparents avec un trait fin gravé dessus pour guider le regard.

Le nomogramme précédent, vu en perspective, a l’air plus classique avec ses trois courbes cotées, sauf qu’une des courbes est réduite à un point (en haut au centre) :

En graduant doublement l’un des segments, on dispose d’une méthode graphique pour calculer la composée de deux fonctions par manipulation débranchée.

Une fois qu’on a nomographié la fonction F de répartition d’une loi normale centrée réduite, on peut la placer sur deux axes gradués parallèles, l’axe entre les deux axes portant la différence entre F(b) et F(a), qui est la probabilité qu’une variable normale centrée réduite soit entre a et b :

Il suffit alors de centrer et réduire (ce qui est faisable avec une calculatrice 4 opérations) une variable aléatoire normale, pour pouvoir utiliser ce nomogramme et « calculer » des probabilités la concernant. Avec ce nomogramme, la calculatrice graphique n’est plus nécessaire en examen...

Le dessin d’une grille fine pour guider le regard est déjà présent chez Louis Ézéchiel Pouchet au XVIIIe siècle. Mais il s’agit d’un abaque tout fait et sur lequel on n’est pas censé ajouter de construction.

À la fin du XIXe siècle, d’Ocagne propose comme on l’a vu ci-dessus, la méthode nomographique pour simplifier les manipulations et alléger le graphique : la grille n’est pas nécessaire pour utiliser un nomogramme.

Mais peu après, John Perry (ingénieur) publie (en 1899) le livre Practical Mathematics dans lequel il conseille l’usage du papier grillagé (l’unité étant le pouce et non le centimètre) pour enseigner les fonctions en école d’ingénieur :

Selon Perry, l’exercice (présenté comme une remédiation : relief work) consistant à placer beaucoup de points sur le papier quadrillé pour tracer la courbe, permet aux élèves de se poser spontanément la question des valeurs de x qui annulent la fonction...

En France, peu après, Jules Tannery propose ce genre d’activités au bac dit « de philo » (équivalent du bac L).

Plutôt que calculer une intégrale en comptant les petits carreaux, Perry propose de la mesurer, à l’aide d’un planimètre :

L’expérience vaut la peine encore aujourd’hui, d’être tentée. Pour cela il faut se procurer ou fabriquer un planimètre, qui n’est pas nécessairment d’Amsler. Par exemple un planimètre à cône peut faire l’affaire. L’article cité juste avant se termine par

En observant le planimètre, en comprenant son fonctionnement si simple, il nous semble qu’on peut mieux appréhender le concept d’aire et qu’on pourra par la suite comprendre des choses plus compliquées et plus « modernes ».

(Étienne Ghys et Jos Leys)

Pour en savoir plus sur les planimètres :

• cet article de Pour la Science
• la fin de cet article de Repères IREM
• écrit par Amsler lui-même

Pas besoin de papier millimétré pour cette activité : on peut distribuer aux élèves des feuilles d’énoncé ( « polycopié » ) portant un carré et quelques représentations graphiques de fonctions, avec des segments verticaux pour montrer les bornes de l’intégrale. Puis on fait mesurer à l’aide du planimètre, l’aire du carré (entraînement mais aussi calibration) et celles des domaines délimités par les représentations graphiques. En faisant effectuer de multiples fois ces mesures, on fait apparaître expérimentalement le fait que le quotient de chaque aire par celle du carré ne dépend ni du planimètre, ni de l’échelle : notion d’unité d’aire...

Une fois qu’on sait représenter graphiquement les fonctions trigonométriques (par exemple en lisant les coordonnées de points sur le cercle unité), on peut les étendre tout aussi graphiquement :

En effet cela met en œuvre les constructions de symétriques de points et permet de se (re)familiariser avec les symétries, par la manipulation.

Perry recommande de faire tracer vraiment (et pas seulement regarder) les représentations graphiques de fonctions puissances et exponentielles :

Il recommande d’en faire un travail collaboratif (une courbe par élève) avec mise en commun des résultats obtenus :

Certes il suffit de regarder le résultat ci-dessus pour constater que 1^{n’importe quoi}=1, mais regarder ne suffit pas forcément pour retenir.

Une fois que les élèves sont familiarisés avec la représentation graphique de fonctions, et alors seulement, Perry leur fait constater que la représentation graphique d’une fonction affine est une droite :

En effet, si l’on enseigne trop tôt aux élèves que représenter graphiquement une fonction affine nécessite moins de placements de points parce qu’il suffit de deux points pour déterminer une droite, on risque de développer chez eux une confusion entre fonctions affines et fonctions en général. J’ai fréquemment constaté ce genre de confusion en 2nde.

Perry propose d’introduire la notion de pente uniquement après avoir représenté graphiquement plusieurs droites parallèles, en nombre suffisant pour avoir créé soi-même la compétence tracé d’une droite connaissant les coordonnées de deux points.

En France au début du XXe siècle, Tannery conseillait, pour se familiariser avec la fonction x², de « construire avec soin [...] un grand nombre de points » :

Ce conseil n’a guère vieilli...