En hommage à mon père, Monsieur Biya.
Dans un récent courrier, l’auteur de l’article écrivait : au lieu du tableau de Biya, il faudrait plutôt parler de tableau de Venn-Hekdjara. Ce nom paraît plus adapté pour son introduction dans les manuels scolaires. En effet, le nom Venn renvoie au logicien anglais John Venn qui établit le diagramme de Venn en 1881 et Hekdjara renvoie à Hekeu Djambou Raoul, du nom de l’auteur du principe qui s’inscrit à la suite de John Venn.
NDRL : Cet article sort du cadre habituel de MathémaTICE : il ne parle pas de TICE et traite une question mathématique un peu marginale dans les programmes français. Nous le publions cependant, comme salut amical à nos collègues africains, et pour confirmer notre ouverture à leurs éventuelles contributions. Et aussi parce qu’il propose une intéressante série d’exercices.
Le Cameroun est un pays qui a deux systèmes éducatifs : le système anglophone et le système francophone. L’objet de cet article, l’enseignement de la notion d’intersection d’ensembles, correspond aux classes de seconde (form five) dans le système anglophone et pour le système francophone aux classes de première de toutes les spécialités. En fonction de la spécialité, les exigences sont différentes, mais cette notion reste à acquérir dans toutes les classes de première, L (littérature) ou S (scientifique). Cette notion d’intersection s’inscrit dans le cadre de la théorie des ensembles élaborée pour la première fois en 1880 par Cantor [1]. Ce dernier jeta les bases de la notion d’intersection qui s’énonce comme suit :
Soit A et B deux ensembles. L’intersection de A et de B se note A∩B et désigne l’ensemble des éléments qui sont à la fois dans A et dans B.
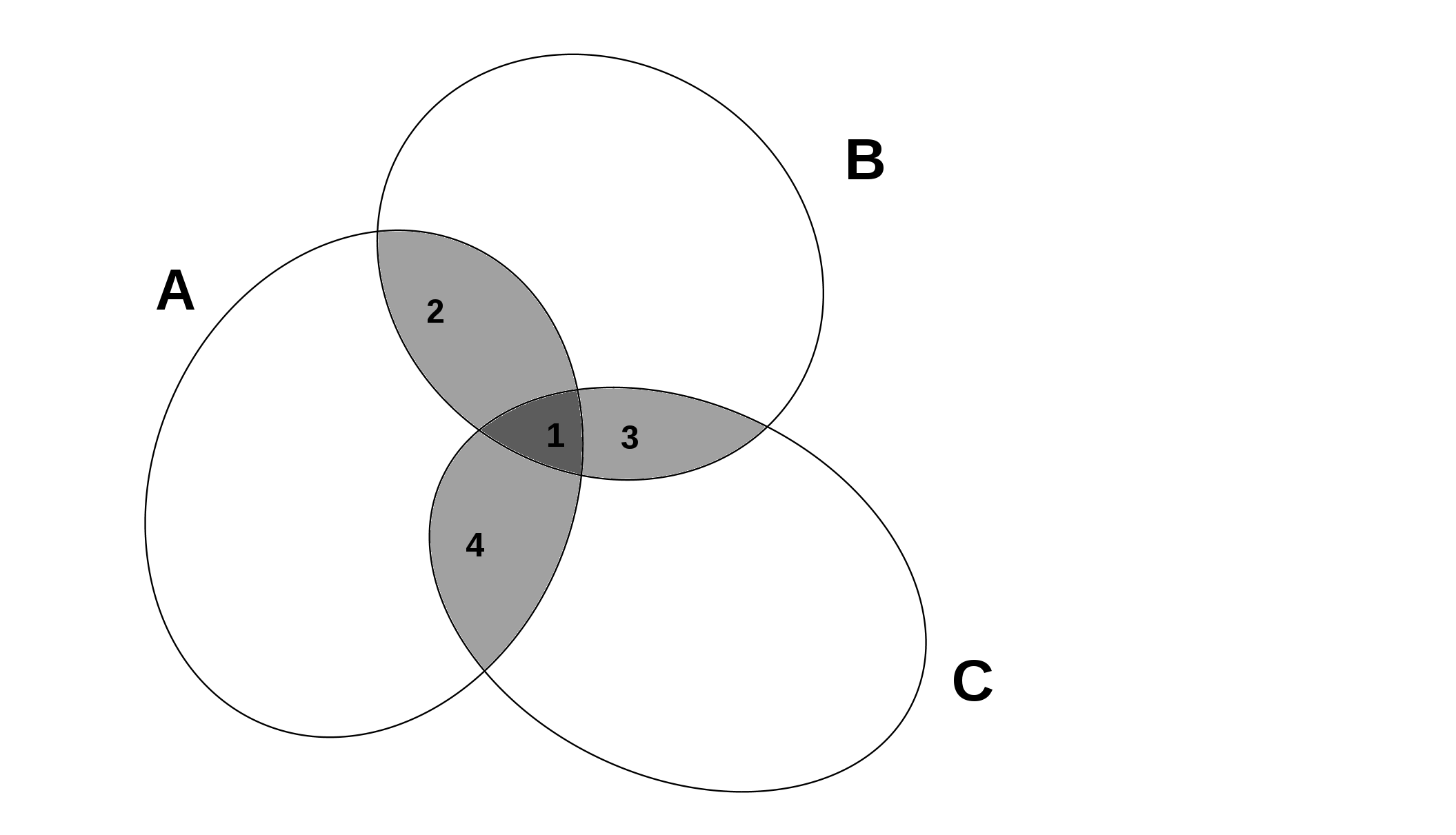
Même si la notion d’intersection n’est qu’une petite partie d’une théorie très importante, elle est utile dans tous les domaines des mathématiques : analyse, probabilités, algèbre, géométrie. De nombreux autres mathématiciens et logiciens ont contribué à sa compréhension et son extension. Le cas du logicien John Venn [2], avec son célèbre diagramme de Venn élaboré en 1881 est d’un intérêt tout particulier, puisqu’il tente d’illustrer et de représenter la notion d’intersection en utilisant des diagrammes. Ces représentations, très utiles pour deux ou trois ensembles se révèlent bien complexes, pour plus de trois ensembles, comme il le confesse avec regret ; Venn dans Symbolic logic propose des schématisations utilisant des ellipses pour illustrer les intersections d’un plus grand nombre d’ensembles, cependant ces représentations restent délicates à manipuler. Notre objet est de généraliser le raisonnement du diagramme de VENN de manière simple et claire. Pour ce faire, il s’agit de définir tout d’abord les « Tableaux de Biya », d’en montrer leur construction et de donner quelques applications en analyse combinatoire.
Limite du diagramme de Venn
Sur le diagramme de Venn de la figure 1, la zone notée 1 est l’intersection des trois ensembles A, B et C, 2 correspond à zone des éléments qui sont à la fois dans A et dans B mais qui ne sont pas dans C, 3, la zone des éléments qui sont à la fois dans B et dans C mais qui ne sont pas dans A et enfin, 4, la zone des éléments qui sont à la fois dans A et dans C mais qui ne sont pas dans B.
Pour quatre ensembles, même si Venn propose des représentations utilisant des ellipses (Figure 2) il n’en demeure pas moins que cette représentation est vite limitée et peu évidente à reproduire.
A titre de rappel, près d’un siècle après les travaux de John VENN, un généticien, statisticien et évolutionniste britannique A.W.F. Edwards [3] publia dans son livre intitulé Cogwheels of the Mind une représentation acceptable de toutes les intersections au delà du cadre habituel de 3 ensembles. Cette représentation n’est cependant pas enseignée dans les programmes scolaires de mathématiques au lycée du fait de la complexité des dessins.
Définition du Tableau de Biya
Le Tableau de Biya est la représentation de toutes les intersections d’un nombre fini d’ensembles.
Prenons l’exemple de l’intersection de trois ensembles A, B et C :
Le nombre de ligne d’un tableau de Biya concernant n ensembles est bien sûr de n. Le nombre de colonne est 2n −n −1 ; en effet, il s’agit de dénombrer les combinaisons de n, n-1,..., 2 éléments parmi n, c’est à dire de calculer :
Ainsi pour quatre ensembles, le tableau comptera 16-4-1 = 11 colonnes :
On peut le construire en séparant les intersections de deux et trois ensembles :
Pour cinq ensembles, le tableau comptera 26 colonnes que l’on peut construire progressivement :
Application du Tableau de Biya en analyse combinatoire
Application 1
En ayant montré la construction d’un tableau de Biya à trois éléments, on peut demander aux élèves de construire un même tableau à 4 ensembles A, B, C et D. Il peut être intéressant de demander aux élèves de prévoir le nombre de colonnes des tableaux intermédiaires puis du tableau complet puis enfin, de faire compléter le tableau de Biya pour les intersections des ensembles pris deux à deux :
Puis pris trois à trois :
Et enfin de faire construire le tableau complet.
Application 2
Pour un tableau à cinq ensembles, prévoir à l’avance le nombre de colonnes des tableaux intermédiaires est bien sûr important pour ne pas oublier de cas. On pourra alors relier le nombre de colonne avec les combinaisons de k parmi n :
Le travail demandé pourrait donc être la construction de ce tableau avec une réflexion sur la généralisation à n ensembles.
Application 3
Une discussion débute au sein de l’équipe nationale de football du Cameroun sur le choix d’un capitaine et de deux vices capitaines. Hamidou Souleymanou, Benoit Assou-Ekotto, Samuel Eto’o, Geremi Njitap, Eyong Takang Enoh sont les prétendants au titre.
A votre avis quels sont tous les trios possibles ?
Solution
Il s’agit ici de dénombrer et d’exprimer les combinaisons de trois parmi cinq,
il ne reste plus qu’à les écrire explicitement
Trio 1 : HAMIDOU, ASSOU, ETO’O.
Trio 2 : ASSOU, ETO’O, NJITAP.
Trio 3 : ETO’O, NJITAP, ENOH.
Trio 4 : HAMIDOU, ASSOU, NJITAP.
Trio 5 : HAMIDOU, ASSOU, ENOH.
Trio 6 : HAMIDOU, ETO’O, NJITAP.
Trio 7 : HAMIDOU, ETO’O, ENOH.
Trio 8 : HAMIDOU, NJITAP, ENOH.
Trio 9 : ASSOU, ETO’O, ENOH.
Trio 10 : ASSOU, NJITAP, ENOH.
Application 4
Dans un lycée comportant 2400 élèves, on effectue une enquête où l’on dénombre :
1260 élèves qui étudient l’anglais
500 élèves qui étudient l’italien
353 élèves qui étudient l’espagnol.
Par ailleurs, on sait que :
210 élèves étudient à la fois l’anglais et l’italien.
164 élèves étudient à la fois l’anglais et l’espagnol.
139 élèves étudient à la fois l’italien et l’espagnol.
25 élèves étudient à la fois l’anglais, l’italien et l’espagnol.
- Représenter un diagramme de la situation précédente.
- Déterminer le nombre d’élèves qui étudient uniquement chaque langue.
- Déterminer le nombre d’élèves qui n’étudient aucune des trois langues.
Solution
La première résolution utilise la représentation de Venn, comme le montre la figure 3.
Le nombre d’élèves qui n’étudient aucune langue :
2400- 25- 139- 114- 185- 911- 176- 75= 775
Utilisons alors le tableau de Biya pour résoudre ce problème :
Construisons le pas à pas :
Une fois les quatre colonnes remplies, on applique les données ; la première colonne correspond aux élèves apprenant les trois langues, il y en a 25.
Les trois colonnes suivantes correspondent aux intersections deux à deux :
la deuxième colonne correspond aux élèves faisant de l’anglais et de l’espagnol ; il y en a au total 164 dont 25 apprennent les trois langues. Donc, il y a 164-25 élèves apprenant exclusivement l’anglais et l’espagnol. De la même façon, on trouve 114 élèves qui apprennent l’italien et l’espagnol et 185 qui apprennent l’anglais et l’italien.
Si on considère la première ligne, on a compté : 25+139+185= 326 élèves qui apprennent l’anglais et au moins une autre langue. Comme on sait que 1260 élèves étudient l’anglais, il y en a 1260-326=911 qui étudient l’anglais seul.
Les autres lignes se remplissent de la même façon.
Pour répondre alors à la dernière question, il suffit alors de soustraire à 2400 le nombre d’élèves qui pratiquent au moins une langue :
2400-25-139-114-185-911-176-75=775.
Application 4
Lors d’une enquête dans une salle de classe on dénombre :
60 élèves qui étudient l’anglais.
38 élèves qui étudient l’italien.
40 élèves qui étudient l’espagnol.
26 élèves qui étudient le français.
Par ailleurs, on sait que :
10 élèves étudient à la fois toutes les quatre langues.
16 élèves étudient à la fois l’anglais, l’italien et l’espagnol.
Aucun autre élève n’étudie seulement trois langues.
20 élèves étudient à la fois l’anglais et l’italien.
21 élèves étudient à la fois l’italien et l’espagnol.
24 élèves étudient à la fois l’anglais et l’espagnol.
Aucun élève n’étudie l’anglais et le français, ni l’italien et le français, ni l’espagnol et le français.
- Représenter un tableau de Biya de la situation précédente.
- Déterminer le nombre d’élèves qui étudient uniquement chaque langue.
- Déterminer le nombre d’élèves interrogés lors de cette enquête.
Solution
La résolution par un diagramme de Venn devient ici délicate ! Voyons comment utiliser les tableaux de Biya :
En lisant par ligne,
60 élèves étudient l’anglais, mais 10 étudient aussi les trois autres langues, 6 l’étudie avec l’italien et l’espagnol, 4 avec l’italien tout seul et 8 avec l’espagnol : 32 élèves étudient donc l’anglais seul.
On pourra de la même façon calculer le nombre d’élèves qui n’étudie qu’une langue. On obtient :
Italien : 13
Espagnol : 11
Français : 16
Le nombre d’élèves interrogés est donc, le nombre d’élèves qui étudient une seule langue plus le nombre d’élèves qui étudient seulement deux langues, plus le nombre d’élèves qui étudient seulement trois langues et enfin le nombre d’élèves qui étudient les quatre langues :
(32+13+11+16)+(4+8+5)+(6)+(10)=105 ; il y a donc 105 élèves qui ont participé à ce sondage.