David Crespil, l’auteur de l’article qui suit, nous écrit :
"Aymeric Picaud a une fois de plus réalisé une belle mise en page qui, je l’espère donnera l’envie au lecteur de prendre contact avec ce sujet aux connaissances mathématiques très abordables. Peut être ce lecteur ne regardera-t-il plus la Lune de la même façon en découvrant la performance de Galilée il y a 400 ans.
Je tiens donc exprimer mes plus vifs remerciement à Aymeric Picaud dont la collaboration s’est exercée sur l’ensemble de mes sujets avec un dévouement qui ne s’est jamais démenti."
N.D.L.R : David Crespil a récrit une nouvelle version de l’article qui lui donne pleinement satisfaction. À sa demande, nous substituons la nouvelle version à la forme initiale. Cela a été aussi l’occasion d’actualiser certains liens.
Nous tenons à remercier David pour l’ensemble de ses articles accessibles depuis cette page dont beaucoup peuvent servir d’inspiration pour des activités en classe à différents niveaux.
- Avant de commencer
- Notions mathématiques utilisées
- Notions d’astronomie utilisées
- Logiciels utilisés
- Situations
- Méthodes
- D) Méthode approchée des différences de longitudes (…)
- 1) Les coordonnées sélénographiques
- 2) Projection orthogonale d’un segment
- 3) La colongitude
- 4) Le logiciel SalsaJ et le logiciel Atlas virtuel de la (…)
- E) Une nouvelle situation : mesurer la hauteur minimale (…)
- 1) Méthode de Galilée
- 2) Régions non éclairées de la Lune et proches du (…)
- F) Méthode de l’angle de phase qui ne tient pas compte (…)
- G) Influence de la sphéricité du sol lunaire
- 1) Qu’entraîne la non prise en compte de la sphéricité (…)
- 2) Méthode tenant compte de la sphéricité de la Lune

- Vue de la montagne au centre du cratère Tycho
- https://www.nasa.gov/images/content/576883main_062911b.jpg
Avant de commencer
Notions mathématiques utilisées
- le théorème de Pythagore
- la trigonométrie sphérique
- la trigonométrie plane
- angles alternes internes
- les équations du second degré
- projection orthogonale d’un segment sur un plan
- distance de deux points en repère orthonormé de l’espace
Notions d’astronomie utilisées
- le terminateur de la Lune
- longitude et latitude sélénographique
- angle de phase
Logiciels utilisés
- MoonShad [1] disponible sur cette page du site de Philippe Boeuf http://robert-space.fr/logiciels.htm [2]
- SalsaJ disponible sur le site http://www.fr.euhou.net/
- Atlas virtuel de la Lune disponible sur le site https://www.ap-i.net/avl/fr/start
- Coelix disponible sur le site https://www.ngc7000.com/fr/coelix/
Introduction
J’ai tenu dans cet article à présenter quelques méthodes permettant de mesurer la hauteur d’une montagne lunaire ou la profondeur d’un cratère lunaire.
La rigueur mathématique déployée pour tenir compte de la sphéricité lunaire dans la méthode de calcul de la hauteur d’une montagne lunaire par B. Morando est des plus instructives. Différents logiciels seront mis à contribution tels le logiciel MoonShad, le logiciel SalsaJ, l’Atlas virtuel de la Lune, le logiciel Coelix qui fourniront toutes sortes d’indications utiles sur le plan astronomique.
Bien sûr, nous n’avons pas oublié Galilée qui il y a 400 ans environ déterminait la hauteur minimale d’une montagne lunaire en procédant lors d’un quartier de lune.
A) Comment les rayons du Soleil arrivent-ils sur la Lune ?


Quelques précisions :
- Soit (P) le plan passant par le centre de la Lune et orthogonal à la droite(TL).
- Soit T le centre de la Terre et L le centre de la Lune.
- De la terre , on voit à peu près la moitié de la Lune.
- Le soleil éclaire environ la moitié de la Lune
- Tout point M de la Lune qui est observé est vu en perspective qui produit le point M’ projeté orthogonal de M sur le plan (P). Ceci sera développé en abordant D/4
Situations
B) Mesure du diamètre d’un cratère de la Lune
D’après un article de Philippe Boeuf reproduit avec l’aimable autorisation de l’auteur.
Il s’agit obtenir la taille d’un cratère lunaire à partir d’une photo dont on ne voit qu’un morceau du limbe (son pourtour).

- document 1
L’astuce sera de déterminer dans un premier temps la taille de la Lune sur l’image, à partir de la forme de son limbe. Ensuite, on comparera la taille d’un cratère mesurée sur l’image avec celle de la Lune obtenue précédemment. Le rapport des deux tailles sur l’image est le même que celui existant en réalité, le diamètre lunaire étant de 3475 km, on aura celui du cratère.
Comment trouver le diamètre d’un cercle connaissant la forme de son limbe ?
Voici notre situation : seule la portion de cercle supérieure est visible.
On peut y mesurer « h » et « L » sans problème, après avoir tracé une corde quelconque sur l’image.
Si on applique le théorème de Pythagore dans le schéma ci-dessous, on trouve :
$$R=\dfrac{h^{2}+L^{2}}{2h}$$

- Schéma 2
Par exemple, sur l’image du document 3, on mesure :
L = 292 pixels, h = 36 pixels
Donc R = 1202 pixels.

- document 3
Quel est le diamètre d’un cratère maintenant ?
Le plus gros situé sur l’image est Aristote. Sur la première image, on estime son diamètre (le grand axe, car à cause de son inclinaison par rapport à nous, il semble elliptique) à 62 pixels.
Une simple proportionnalité nous dit que le cratère lunaire fait en réalité :
$$\dfrac{62 \times 3475}{2404} \approx 90 \text{km}$$
alors qu’un coup d’œil dans un atlas lunaire nous indique qu’il est estimé à 88 km.

- document 4
Voici une image du cratère Archimède (83 km de diamètre d’après les atlas, ce qui peut servir d’échelle). On peut s’en servir pour trouver la hauteur du pic, à condition de connaître la hauteur angulaire du Soleil à cet endroit lors de la prise de vue.
Utilisons le logiciel SalsaJ pour mesurer la longueur de l’ombre.


- document 5
Spécifions l’échelle dans la rubrique analyse (document 6) en exprimant que ce trait a pour longueur environ 84 km.

- document 6

- document 6 bis
Le trait jaune entre le sommet de la montagne et l’extrémité de l’ombre mesure 10 km.
Déterminons à présent la hauteur approximative de la montagne.

- Schéma 7
$$h = \text{SO} \times \sin\left(\widehat{\text{SOB}}\right)$$
Mais comment donc déterminer la hauteur du Soleil ?
On prend en même temps une image « grand champ » de la Lune, où elle sera
visible en entier. Cela donnera :

- document 8
Le logiciel MoonShad produit par Philippe Boeuf (avec l’aimable autorisation de l’auteur) va nous fournir la hauteur du Soleil.
En voici une copie d’écran concernant la situation qui nous occupe :

- document 9
Ce logiciel, très simple d’utilisation, vous permet, après avoir positionné les deux « pôles du croissant » lunaire, de placer le terminateur (en rouge), et le cercle d’égale hauteur du Soleil : celui en bleu qui passe par le cratère Archimède en jaune donne une hauteur de 10° environ.
Dans ce cas :
$$ \text{hauteur (en km)} = 10 \times \sin (10°) \approx 1{,}75$$
On l’aura compris, il n’est pas facile de mesurer les ombres avec une grande précision mais on obtient tout de même une approximation honorable.
Important :
On veillera en allant sur propriétés à renseigner les rubriques de compatibilité : ainsi avec Windows 8 (et supérieurs), il faut avoir le panneau suivant :

- Réglage de compatibilité (MoonShad)
Méthodes
D) Méthode approchée des différences de longitudes sélénographiques
Les paragraphes 1, 2 et 3 sont destinés à préparer le paragraphe 4.
1) Les coordonnées sélénographiques

- Schéma 10
- Le cercle (C) est l’équateur lunaire
- A origine des longitudes
Les coordonnées sélénographiques sont à la Lune ce que sont les coordonnées géographiques à la Terre.
Il existe un méridien origine en vert par rapport auquel on mesure la longitude de m qui en valeur arithmétique est égale à la mesure de l’arc Am
La longitude est affecté du signe + à l’Est et - à l’Ouest d’après les conventions
de l’UAI (union astronomique internationale).
La latitude est en valeur arithmétique la mesure de l’arc Mm et se trouve affectée du signe + dans l’hémisphère Nord et - dans l’hémisphère Sud.
Les expériences de télémétrie laser ont permis de bien définir ce système de coordonnées.
2) Projection orthogonale d’un segment

- Schéma 11
Théorème : $ab=AB \cos \alpha$
$\alpha$ désigne l’angle que fait $(\text{AB})$ avec le plan de projection.
À insérer
3) La colongitude

- Schéma 12
Le terminateur est la ligne de séparation entre la partie sombre et la partie éclairée de la Lune (Voir Schéma 12).
En rouge la partie de la Lune éclairée par le Soleil.
En vert la partie de la Lune visible de la Terre.
Entre les deux la partie de la Lune visible de la Terre et éclairée par le Soleil.
Tous les points du terminateur ont même longitude.
Les tables de l’atlas lunaire fournissent une donnée que l’on appelle la colongitude c reliée à la longitude L du terminateur par :
- De la nouvelle lune au premier quartier : $\textL = 360°-\textc\text Est (1)$
- Du premier quartier à la pleine lune : $\textL = \textc\text Ouest (2)$
- De la pleine lune au dernier quartier : $\textL = 180°-\textc\text Est (3)$
- Du dernier quartier à la nouvelle lune : $\textL = \textc-180°\text Ouest (4)$
Exemple : Allons sur les éphémérides de l’atlas lunaire.
Le 7 juin 2012, on est entre la pleine lune et le dernier quartier comme l’indique le premier tableau ci-dessous. C’est donc la formule (3) qui s’applique.
La colongitude vaut $121,5°$. Donc la longitude du terminateur vaut
$$180°-121,5°= 58,5°$$
|
|
Cliquons sur un point du terminateur, on obtient le cratère Webb et par l’onglet information nous obtenons que sa longitude est $59,99°$ Est. Ce qui est normal puisque le cratère n’est pas exactement sur le terminateur.

- Illustration
4) Le logiciel SalsaJ et le logiciel Atlas virtuel de la Lune
Utiliser le logiciel Atlas virtuel de la Lune

- document 13
- Le point rouge désigne le cratère TYCHO.
Données et photos extraites de : http://www.sciencesalecole.org/
Utiliser le logiciel SalsaJ, ouvrir cette image de la lune obtenue sur l’atlas virtuel de la lune le 10 janvier 2014 à 12 h 49 min 58 s UT.
Prendre l’outil sélection rectiligne et tracer sur l’image un diamètre de la Lune.

- document 14
- La ligne jaune correspond au diamètre de la Lune
Entrez dans « Analyse » puis « indiquer l’échelle ».
Dans la fenêtre qui va s’ouvrir, entrer la distance réelle de la Lune (3476 km) et l’unité de mesure en km et faire « Oui ». Vous pouvez désormais mesurer la longueur de l’ombre d’un cratère en km.

- Schéma 15
- réglage de l’échelle
Après agrandissement de la zone du cratère, on trouve 25,23 km environ pour la longueur de l’ombre.
Avec le logiciel Atlas virtuel de la Lune, nous notons :
- Longitude du cratère TYCHO = 11,2° Ouest
- Colongitude du terminateur = 21,7°
Le 10 janvier 2014 on est entre le premier quartier et la pleine lune.
C’est donc la formule (2) de D/3 qui s’applique : la longitude ouest du terminateur est égale à sa colongitude et vaut 21,7°.

- Schéma 16
Notations :
- S centre du soleil
- t centre de la terre
- O le centre de la lune
- (P) plan du terminateur : (P) est le plan perpendiculaire en O à la droite(OS)
- (Q) le plan qui détermine la visibilité depuis la terre : (Q) est le plan perpendiculaire en O à la droite (Ot)
- P sommet d’une montagne ou sommet d’un cratère
- B la base de la montagne ou du cratère ici le cratère Tycho
- c = la longitude sélénographique du terminateur, c’est à dire la longitude du
point U - b = longitude sélénographique de B
- L = longitude sélénographique de la terre , c’est-à-dire du point W donnée par les éphémérides
- Le cercle en noir est l méridien du point T
- Le cercle en marron est l’intersection de la sphère lune avec le plan Q
- En jaune le demi-cercle du terminateur
- K l’intersection du rayon solaire passant par P avec le plan horizontal du point B
- Z intersection de (PK) avec le plan (Q)
- T l’intersection de ce rayon avec le plan (P) plan du terminateur
- R projection orthogonale de T sur le plan (Q)
Calculs
Les flèches indiquent les passages ou nous consentons à des approximations.
L’ombre est le segment [BK].
Alors si B n’est pas trop éloigné de l’équateur lunaire, on a schéma 16 :
$\widehat{\text{BOT}} \approx \widehat{\text{DOE}} = \widehat{\text{UOE}} = |b − c|$ et donc $\widehat{\text{BOT}} \approx |b − c| = 10,5°$ ←
Les angles $\widehat{\text{BKP}}$ et $\widehat{\text{BOT}}$ sont des angles à côtés perpendiculaires donc égaux.
Or dans le triangle rectangle KBP, l’angle $\widehat{\text{BKP}}$ représente l’angle que fait le Soleil avec l’horizon et l’on a : $\tan \widehat{\text{BKP}} = \dfrac{\text{BP}}{\text{PS}}$ donc $\tan \widehat{\text{BOT}} = \dfrac{\text{BP}}{\text{PS}}$
BP est la hauteur cherchée : $\text{BP} = \tan \text{PS}\times \widehat{\text{BOT}}$
PK est la longueur réelle. La longueur apparente (lue sur la photo) est de 23,5 km.
Le jour de l’observation, la longitude sélénographique de la terre vaut environ 5° [3], celle du terminateur 21,7°
Alors $\widehat{\text{RZT}} = \widehat{\text{UOW}}\text{ (angles à côtés perpendiculaires ) }= 21,7°- 5° =16,8°$
Si en première approximation, on considère que W est l’origine des longitudes alors :
$\widehat{\text{RZT}} \approx |c|$ avec $c$ longitude du terminateur.←
Appliquons alors le résultat du paragraphe D/2. Vous pouvez consulter le document ci dessous pour plus d’explications.
- Explication sur la distance réelle et la distance apparente
- Voir ce document pour plus d’explications
$d_{\text{apparente}} = d_{\text{réelle}} \times \cos \widehat{\text{RZT}} \approx d_{\text{réelle}} \times \cos(21,7°)$
$\text{PK} = d_{\text{réelle}} = \dfrac{25,23\text{ km}}{\cos(21,7°)}$ soit environ 27,15 km
La hauteur cherchée est donc en km : $\tan(10,5°) \times 27,15 \approx 5$
Cette valeur est proche de celle indiquée par l’Atlas qui indique 4 800 m.
Si on recherche une plus grande précision $\text{PK}=d_{\text{réelle}}=\dfrac{25,23\text{ km}}{\cos(16,8°)}=26,35\text{ km}$
La hauteur cherchée est donc en kilomètres : $26,35 \times \tan(10,5°)\approx 4,84$
La méthode proposée depuis le début du paragraphe est d’autant meilleure que la montagne dont on mesure la hauteur est près de l’équateur.
Que donne le logiciel MoonShad ?
Le mode de fonctionnement est donné dans le logiciel.
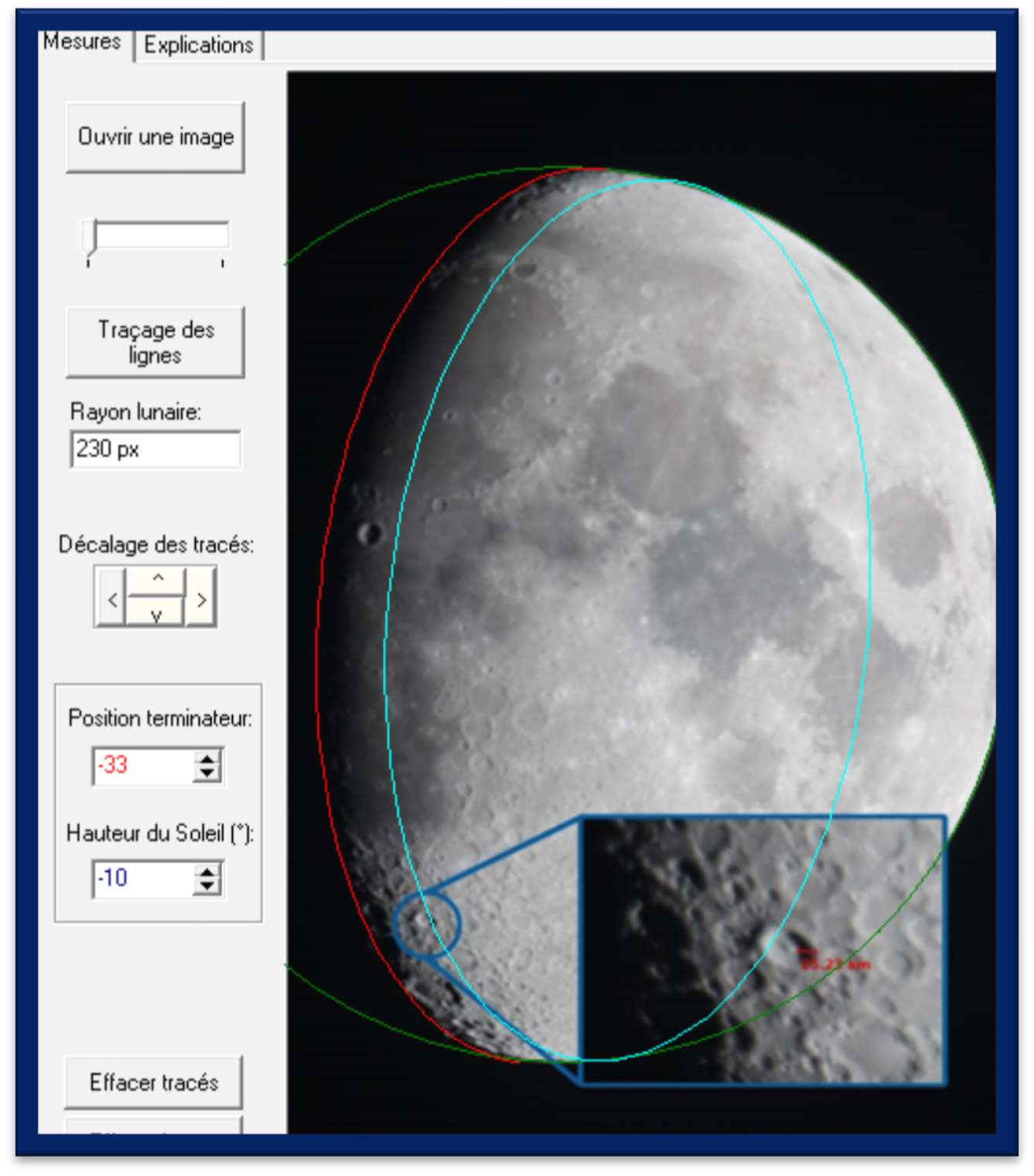
- document 17
- utilisation de MoonShad
La hauteur cherchée vaut : $25,23\times \tan(10°) \approx 4,44\text{ km}$ soit 4450 m.
La différence avec le résultat exact vient de ce que l’on essaye de positionner au mieux le terminateur.
Cependant cette méthode avec le logiciel MoonShad donne un ordre de grandeur satisfaisant.
Ne pas tenir compte du signe $-$ pour les hauteurs et partir du terminateur avec l’arc bleu pour rejoindre le cratère. (Le logiciel présente quelques bugs non rédhibitoires ).
E) Une nouvelle situation : mesurer la hauteur minimale d’un sommet éclairé
1) Méthode de Galilée
La méthode est simple. Elle permet de calculer la hauteur d’une montagne dont le sommet est éclairé dans la zone sombre située le long du terminateur.

- document 18
Dans le document suivant :
Le terminateur est celui du premier quartier.
Les flèches désignent des points lumineux.

- document 19
- lien : http://images.math.cnrs.fr/Il-y-a-quatre-cents-ans-Sidereus.html
source : images des mathématiques
Ce qui suit est un développement et une justification mathématique de l’idée de Galilée qui conduit à l’évaluation de la hauteur minimale de la montagne.

- Schéma 20
- n et s désignent respectivement les pôles nord et sud de la lune.
- O centre de la lune, A la base de la montagne, D le sommet de la montagne.
C le point de rencontre du terminateur avec le rayon lumineux éclairant le point D de la montagne qui n’est peut être pas son sommet. Les points E, A, D sont donc alignés.
Appelons K le sommet.
La hauteur de la montagne est donc supérieure ou égale à AD.
N et M les projections respectives de C et D sur le plan (Q) en marron, limite de visibilité depuis la Terre. Le terminateur coïncide avec l’axe Nord-Sud de la Lune puisque nous sommes à l’un des deux quartiers de la Lune.
Au premier quartier, le terminateur en projection orthogonale est un segment de droite perpendiculaire à l’équateur lunaire.
Par conséquent MN mesuré sur une photo sera égale à CD, M et N étant les projections orthogonales respectives de D et C sur le terminateur.
On a : $\left(R+AD\right)^{2}=DC^{2}+R^{2}$
avec $R\approx 1734\text{ km}$ le rayon de la Lune.
Galilée observe des montagnes telles que MN = 1/10 rayon lunaire = 173,4 km
Par exemple la montagne correspondant à la première flèche à partir du haut.
Or MN = DC donc AD ≈ 8,6 km.
Donc la hauteur de la montagne est supérieur ou égale à 8,6 km
Cependant juste avant la disparition dans la nuit lunaire du sommet, on est sûr que K=D et le calcul précédent fournit alors exactement la hauteur de la montagne.
Supposons la montagne répertoriée. On procède alors aux étapes suivantes :
- étape 1 : on prend la photo de la lune au moment de l’extinction du sommet.
- étape 2 : on se reporte à l’atlas virtuel de la Lune et l’on met le calendrier à la date et à l’heure de la prise de photo de la montagne, c’est-à-dire au moment de l’extinction du sommet.
- étape 3 : on mesure la distance de la montagne au terminateur et l’on recommence le calcul qui vient d’être fait.
À l’époque de Galilée, le rayon de la lune était estimé au double de ce qu’il vaut réellement et de fait les hauteurs fournies par Galilée étaient fausses mais la méthode était très astucieuse.
2) Régions non éclairées de la Lune et proches du terminateur, l’angle phase étant quelconque

- Schéma 21
- T centre de la terre non figuré ici.
- (P) plan perpendiculaire à la droite (OT)
- C le terminateur
- C’ sa projection sur P (une ellipse)
- k la base de la montagne M son sommet
- O centre de la lune
- n et h les projections orthogonales de N et H sur le plan P.
- $R$ est le rayon de la Lune
Par h, on mène la perpendiculaire à l’axe de la lune (droite en bleu). Elle rencontre le terminateur précisément au point n.
La distance nh sera lue sur la photo et de plus $\text{nh} = \text{NH} \sin \vartheta $.
Appelons $a$ l’altitude de H $a=\text{HK}$ posons $\omega=\widehat{\text{HON}}$ et $d=\text{NH}$
$\tan\omega=\dfrac{d}{R}$
$(R+a)\cos \omega = R$
$a=R\dfrac{1-\cos\omega}{\cos\omega}=2R\dfrac{\left(\sin\dfrac{\omega}{2}\right)^{2}}{\cos\omega}$
$a\approx R\dfrac{\omega^{2}}{2}\approx \dfrac{d^{2}}{2R}$
L’altitude de M est supérieure à $a$, mais égale à $a$ lorsque M disparaît dans le nuit lunaire.
La distance $d’$ mesurée sur le cliché est $d’=d\sin\vartheta$ où $\vartheta$ est l’angle de phase.
Donc : $\boxed{a\approx\dfrac{d’^{2}}{2R\left(\sin\vartheta\right)^{2}}}$
On pourra vérifier que c’est un cas particulier de la formule (1) du paragraphe G.
F) Méthode de l’angle de phase qui ne tient pas compte de la sphéricité du sol lunaire

- Schéma 22
En jaune le rayon solaire passant par le sommet de la montagne.
Soit I la base de la montagne, J le sommet de la montagne : deux options vont se présenter selon que les calculs tiendront ou non compte de la sphéricité de la Lune.
Nous allons nous servir dans ce paragraphe du point K intersection du rayon solaire avec le plan horizontal en I.
En réalité, le rayon solaire perce la lune au point J’.
Tenir compte de la sphéricité lunaire signifie que nous n’utiliserons pas le point K mais le point J’.
Le calcul de la hauteur de la montagne sera fonction du point K ou J’ que l’on aura choisi.
Si c’est du point K, le calcul sera plus simple mais moins précis comme nous allons le voir.
Selon la convention adoptée par l’UAI, les longitudes Est sont positives, les Ouest sont négatives.
Considérons à présent le schéma 23
Notations
- N et S les pôles Nord et Sud respectivement
- I base de la montagne lunaire
- J sommet de la montagne
- K intersection du rayon lumineux passant par le sommet J avec le plan horizontal du lieu I
- Appeleons T le centre de la Terre et O le centre de la Lune
- En noir le méridien du lieu I qui coupe l’équateur lunaire en D
- (Q) le plan perpendiculaire en O à la droite (TO)
- Le cercle en marron est l’intersection de la sphère lune avec le plan (Q)
- F étant la projection orthogonale de K sur (Q) et B étant la projection orthogonale de J sur (Q)
- L’angle $\widehat{\text{JKI}}$ est l’angle que fait le rayon solaire avec le plan horizontal. Appelons cet angle $\alpha$
- $\vartheta$ désigne l’angle de phase $(\overrightarrow{OW},\overrightarrow{OE})$
- A origine des longitudes
- Le repère (OX, OY,OZ) est orthonormé

- Schéma 23
Le point W est très proche de A origine des longitudes.
Calculs
Le triangle JKI est rectangle en I.
On a $\widehat{\text{KJI}}=\widehat{\text{JOE}}$ angles alternes-internes
On a $\widehat{\text{KJI}}=\widehat{\text{IOE}}=\dfrac{\pi}{2}-\alpha$
Dans un triangle ABC sphérique rectangle en C on a :
Considérons alors le triangle sphérique IFE rectangle en F :
On a :
- $\overset{\frown}{\text{FE}}=\vartheta-\delta$ avec $\delta$ longitude du lieu qui peut être positive ou négative
- $\overset{\frown}{\text{IF}}=\varphi$ avec $\varphi$ latitude du lieu
- $\overset{\frown}{\text{IE}}=\dfrac{\pi}{2}-\alpha$ avec $\alpha $ l’angle que fait le rayon solaire avec le plan horizontal
- On note également $\rho=\text{KJ}$, $d=\text{FB}$
On a alors : $\cos\left(\dfrac{\pi}{2}-\alpha\right) = \cos \varphi \cos(\vartheta-\delta)$ d’après (1)
D’où $\sin \alpha= \cos \varphi \cos(\vartheta-\delta)$ (2)
Par ailleurs l’angle que fait la droite (KJ) avec le plan (P) vaut $\dfrac{\pi}{2}-\vartheta$
Appliquons la propriété sur la projection orthogonale d’un segment sur le plan (Q) :
$d=\text{FB}=\text{KJ}\cos\left(\dfrac{\pi}{2}-\vartheta\right)=\text{KJ}\sin\vartheta=\rho\sin\vartheta$ (3)
Dans le triangle plan KJI rectangle en I on a :
$\cos\left(\dfrac{\pi}{2-\alpha}\right)=\dfrac{\text{IJ}}{\text{KJ}}=\dfrac{a}{\text{KJ}}$ avec $a$ hauteur de la montagne.
$\sin\alpha=\dfrac{a}{KJ}$
Si bien que :
$a=d\dfrac{\sin \alpha}{\sin \vartheta}$ (4)
$a=\dfrac{d\cos\varphi\cos(\vartheta-\delta)}{\sin \vartheta}$(6)
Examinons le cas particulier où l’on est sur l’équateur lunaire.
Dans ce cas $\varphi=0$.
La relation (2) $\sin \alpha= \cos \varphi \cos(\vartheta-\delta)$ devient :
$\sin \alpha= \cos(\vartheta-\delta)$ soit $\cos\left(\dfrac{\pi}{2-\alpha}\right)= \cos(\vartheta-\delta)$
$\dfrac{\pi}{2-\alpha} = \vartheta-\delta$
D’où $\alpha=\dfrac{\pi}{2}-(\vartheta-\delta)$ (7)
Selon la convention adoptée par l’UAI, les longitudes Est sont positives, les longitudes Ouest sont négatives.
Examinez les cas particuliers :
$\vartheta = 0°$ ou $\vartheta = 180°$
$\varphi = 90°$ ou $\varphi = -90°$
Résumé
K intersection du rayon lumineux passant par le sommet J avec le plan horizontal du lieu I
Posons : $\vartheta = \text{angle de phase}$, $\varphi =\text{latitude du lieu I}$
$\rho =\text{KJ}$
$d = \text{AB}$ (schéma 23)
$L_{\text{S}}$ et $L_{\text{I}}$ désignant les longitudes sélénographiques du lieu I et du Soleil S.
$\delta=|L_{\text{I}}|$
Si l’on ne tient pas compte de la sphéricité du sol lunaire alors :
$\boxed{a=d\dfrac{\sin \alpha}{\sin \vartheta}}$ (4)
$\boxed{a=\rho \sin\alpha}$ (5)
$\boxed{a=\dfrac{d\cos\varphi\cos(\vartheta+\varepsilon\delta)}{\sin \vartheta}}$ (6)
avec $\varepsilon=\pm 1$
Si $L_{\text{S}}$ et $L_{\text{I}}$ sont de même signe, alors $\varepsilon= -1$
Si $L_{\text{S}}$ et $L_{\text{I}}$ sont de signes contraires, alors $\varepsilon= +1$
G) Influence de la sphéricité du sol lunaire
1) Qu’entraîne la non prise en compte de la sphéricité lunaire ?

- Schéma 25
Supposons que J soit le sommet le plus haut de la Lune (10 km) et que le rayon passant par le sommet J de la montagne coupe le terminateur en J’ (cercle en jaune) et le plan horizontal de I en K . L’angle $\widehat{\text{JKI}}$ est l’angle que fait le rayon solaire avec le plan horizontal. Appelons cet angle $\alpha$.
Les angles $\widehat{\text{DKA}}$ et $\widehat{\text{J’OD}}$ sont des angles à côtés perpendiculaires et donc :
$\widehat{\text{DKA}}=\widehat{\text{J’OD}}$
On a alors : $\cos \alpha= \dfrac{R}{R+a}$ où $R$ rayon de la Lune et $a$ hauteur de la montagne.
Comme $R=1738 \text{km}$ on en déduit $\alpha\approx 6°$.
Calculons DJ’ : $\text{OD}^{2} = \text{J’O}^{2}+ \text{J’D}^{2}$ d’après le théorème de Pythagore.
$\text{J’D} \approx 187 \text{km}$
Si l’on ne tient pas compte de la sphéricité du sol lunaire alors :
$a=\rho \sin \alpha \approx 187 \times \sin(6°) \approx 19,5$
donc $a\approx 19,5\text{ km}$.
La non prise en compte de la sphéricité lunaire peut donc entraîner une erreur
considérable ( 19,5 km au lieu de 10 km) !
Fort de cet exemple, donnons la formule qui permet de connaître de manière précise la hauteur d’un montagne lunaire en tenant compte de la sphéricité de la Lune.
2) Méthode tenant compte de la sphéricité de la Lune
Rappel

- Schéma 26
- Coordonnées sphériques. Les notations sont adaptées aux notations utilisées dans cet article pour les latitudes et longitudes sélénographiques.
- $R$ désigne la distance du point M au centre du repère (centre de la Lune)
- $\delta$ désigne la longitude mesurée depuis l’axe des $x$ généralement entre −180° (Ouest) et 180° (Est)
- $\varphi$ désigne la latitude comprise entre −90° (Sud) et 90° (Nord)
Les formules de changement de variables (coordonnées sphériques M($R,\varphi,\delta$) vers coordonnées cartésiennes M($x,y,z$) ) :
$$ \left\lbrace\begin{array}{l} x=R\cos\varphi\cos\delta\\ y=R\cos\varphi\sin\delta\\ z=R\sin\varphi\\ \end{array}\right. $$
Nous allons à présent évaluer la hauteur de la montagne en tenant compte de la sphéricité de la Lune.
Le rayon provenant du Soleil coupe la Lune en un point J’.

- Schéma 27
A est l’origine des longitudes qui n’est pas rigoureusement l’intersection de (OT) avec la Lune
Le plan de l’écliptique est pratiquement confondu avec celui de l’équateur lunaire.
Notations
- $\delta$ désigne la longitude sélénographique
- $\varphi$ désigne la latitude sélénographique
Posons par ailleurs :
- T le centre de la Terre
- S le centre du Soleil
- A le point origine des longitudes
- O le centre de la Lune
- I la base de la montagne
- J le sommet de la montagne
- K point où le rayon solaire coupe le plan horizontal
- J’ point où le rayon solaire coupe la Lune
- $\vartheta$ désigne l’angle de phase $\left(\overrightarrow{OT},\overrightarrow{OS}\right)$
- $\alpha$ désigne l’angle que font les rayons solaires avec le plan horizontal égale à $\widehat{\text{JKI}}$
- N pôle nord de la Lune
Le cercle bleu est l’équateur lunaire.
Le repère est orthonormé.
Début du calcul de Bruno Morando (1931-1995)
On pose $\text{J}(x,y,z)$ et $\text{J}’(X,Y,Z)$ ainsi que que $\rho$ le module du vecteur $\overrightarrow{\text{JJ’}}$.
Soient $\varphi$ et $\delta$ les coordonnées sélénographiques de I.
On a :
$X=x-\rho\cos\vartheta$, $Y=y-\rho\sin\vartheta$, $Z=z$, $\vartheta=\left(\overrightarrow{OT},\overrightarrow{OS}\right)$.
Exprimons que le point J’ est sur la Lune :
$X^{2}+Y^{2}+Z^{2}=R^{2}$, ce qui donne en posant $a=\text{IJ}$ :
$\rho^{2}-2\rho(a+R)\cos\varphi\cos(\vartheta-\delta)+(a+R)^{2}-R^{2}=0$
En effet, si on utilise le passage des cordonnées sphériques aux coordonnées cartésiennes on a :
$$ \left\lbrace\begin{array}{l} x=(a+R)\cos\varphi\cos\delta\\ y=(a+R)\cos\varphi\sin\delta\\ z=(a+R)\sin\varphi\\ \end{array}\right. $$
D’après la relation (2) du paragraphe F : $\boxed{\cos\varphi\cos(\vartheta-\delta)=\sin\alpha}$
Or ce que nous observons n’est pas la distance J’J mais la projection de cette distance sur le plan perpendiculaire à la ligne de visée.
Cette projection vaut $\boxed{d=\rho\sin\vartheta}$
On a donc l’équation :
$$(a+R)^{2} (\sin \vartheta)^{2} - 2d (a+R) \sin \vartheta \sin \alpha + d^{2} - R^{2} (\sin \vartheta)^{2} = 0$$
C’est une équation du second degré en a+R dont le discriminant est :
$\Delta = (\sin \vartheta)^{2} (R^{2} (\sin \vartheta)^{2} - d^{2} (\cos \alpha)^{2})$ qui est positif si $R^{2} (\sin \vartheta)^{2} - d^{2} (\cos \alpha)^{2}\geqslant 0$
Nous ne devons retenir que la racine ci-dessous :
$$a=\dfrac{d\sin\alpha}{\sin\vartheta}+\dfrac{1}{\sin\vartheta}\sqrt{R^{2}(\sin \vartheta)^{2}-d^{2}(\cos \alpha)^{2}}-R$$
(1)En effet : si $a=0$, $d$ doit être égal à 0.
Fin du calcul de Bruno Morando.
Le calcul de Bruno Morando appelle une remarque :
Il est possible de montrer que le discriminant est toujours positif.
Considérons en effet le triangle OJJ’. Posons $\omega = \widehat{\text{J’OJ}}$.
La règle des trois sinus permet d’écrire : $\text{J’J}=\dfrac{R\sin\omega}{\cos\alpha}$
Les points J et J’ sont projetés en une distance $d=\text{JJ’}\sin\vartheta$
Donc $\sin\omega=\dfrac{d\cos\alpha}{R\sin\vartheta}$ donc $(\sin\omega)^{2}=\left(\dfrac{d\cos\alpha}{R\sin\vartheta}\right)^{2}$
$(\cos\omega)^{2}=1-\left(\dfrac{d\cos\alpha}{R\sin\vartheta}\right)^{2}=\dfrac{\Delta}{R^{2}(\sin\vartheta)^{2}}$ et donc $\Delta\geqslant 0$
À présent si $\rho$ désigne la distance réelle du sommet de la montagne à l’extrémité de l’ombre et $d$ la distance apparente on a :
$\boxed{d=\rho\sin\vartheta}$
Dans ce cas la hauteur de la montagne $a$ s’exprime en fonction de la distance réelle $\rho$ et de l’angle d’incidence du Soleil $\alpha$ par la formule :
$$ \boxed{ a=\rho\sin\alpha+\sqrt{R^{2}-\rho^{2}(\cos \alpha)^{2}}-R } $$
Exemple
Au moment du premier quartier ($\vartheta = 90°$) on trouve que la longueur apparente de l’ombre est 64,22 km et que l’angle $\alpha = 10°$.
La formule (1) de ce paragraphe donne $a = 10 \text{km}$
La formule (4) du paragraphe F : $d = a\dfrac{\sin\vartheta}{\sin\alpha}$ donne $a=11,5 \text{km}$
Résumé
[blue]Avec la courbure :[/blue]
$$ \boxed{ \begin{array}{l} a=\dfrac{d\sin\alpha}{\sin\vartheta}+\dfrac{1}{\sin\vartheta}\sqrt{R^{2}(\sin \vartheta)^{2}-d^{2}(\cos \alpha)^{2}}-R \\ a=\rho\sin\alpha+\sqrt{R^{2}-\rho^{2}(\cos \alpha)^{2}}-R \end{array} } $$
[blue]Sans la courbure :[/blue]
$$ \boxed{ \begin{array}{l} a=\dfrac{d\sin\alpha}{\sin\vartheta} \\ a=\rho\sin\alpha \end{array} } $$
Montrons comment obtenir $\vartheta$ et $\alpha$
Appelons :
- $L_{\text{S}}$ et $l_{\text{S}}$ la longitude et la latitude sélénographique du Soleil
- $L_{\text{T}}$ et $l_{\text{T}}$ la longitude et la latitude sélénographique de la Terre
- $L_{\text{I}}$ et $l_{\text{I}}$ la longitude et la latitude sélénographique du lieu étudié
On trouve par exemple ces données dans la tables des éphémérides physiques de la lune du logiciel Coelix pour ce qui concerne le Soleil et la Terre et les coordonnées sélénographiques du lieu dans le logiciel Atlas virtuel de la Lune.
a) Montrons que $\cos\vartheta=\sin(l_{\text{T}})\sin(l_{\text{S}})+\cos(l_{\text{T}})\cos(l_{\text{S}})\cos(L_{\text{T}}-L_{\text{S}})$

- Schéma 28
Utilisons les formules de Gauss de la trigonométrie sphérique :
On a :
$$ \boxed{ \cos c = \cos a \cos b +\sin a \sin b \cos \gamma } $$
Appliquons cette relation au triangle sphérique TNS du schéma 28.
$$ \cos \vartheta = \cos \left(\frac{\pi}{2}-l_{\text{T}}\right) \cos \left(\frac{\pi}{2}-l_{\text{S}}\right) +\sin \left(\frac{\pi}{2}-l_{\text{T}}\right) \sin \left(\frac{\pi}{2}-l_{\text{S}}\right) \cos \left(L_{\text{T}}-L_{\text{S}}\right) $$
D’où :
$$ \boxed{ \cos \vartheta = \sin \left(l_{\text{T}}\right) \sin \left(l_{\text{T}}\right) +\cos \left(l_{\text{T}}\right) \cos \left(l_{\text{S}}\right) \cos \left(L_{\text{T}}-L_{\text{S}}\right) } $$
On peut aussi obtenir l’angle de phase par les éphémérides de la Lune de l’IMCCE http://vo.imcce.fr/webservices/miriade/?forms
b) Montrons que $\sin\alpha=\sin(l_{\text{I}})\sin(l_{\text{S}})+\cos(l_{\text{I}})\cos(l_{\text{S}})\cos(L_{\text{I}}-L_{\text{S}})$
On peut supposer le plan de l’écliptique non confondu avec le plan de l’équateur lunaire et suivre les explications avec le schéma 28.
Nous allons considérer le triangle sphérique NSI.
$\widehat{\text{J’JI}}=\widehat{\text{JOS}}$ comme angles alternes-internes
Comme le triangle plan J’JI est rectangle en I, l’angle $\widehat{\text{J’JI}}$ a pour mesure $\frac{\pi}{2}-\alpha$ donc pour les mesures d’arcs :
- $\overset{\frown}{IS}=\dfrac{\pi}{2}-\alpha$
- $\overset{\frown}{NI}=\dfrac{\pi}{2}-l_{\text{I}}$
- $\overset{\frown}{NS}=\dfrac{\pi}{2}-l_{\text{S}}$
pour l’angle sphérique INS : $\widehat{\text{INS}}=|L_{\text{I}}-L_{\text{S}}|$
Appliquons : $\cos c = \cos a \cos b +\sin a \sin b \cos \gamma$
Nous obtenons :
$\sin\alpha=\sin(l_{\text{I}})\sin(l_{\text{S}})+\cos(l_{\text{I}})\cos(l_{\text{S}})\cos(L_{\text{I}}-L_{\text{S}})$



