Les listes en compréhension sont des objets qui permettent de générer assez simplement des suites de nombres (voir Notion de liste en dernier paragraphe) :

Voyons maintenant, plus classiquement, le calcul de termes d’une suite définie de manière explicite, c’est-à-dire à l’aide d’une fonction de n.

Après avoir défini la fonction u, on crée une liste vide appelée « suite » dans laquelle on ajoute (append) à l’aide d’une boucle les termes d’indice compris entre début et fin.
Si l’on veut simplement un terme de rang donné, il suffit d’utiliser la fonction u :

Regardons maintenant du côté des suites définies par récurrence :

Après avoir défini la fonction f, qui calcule $u_{n+1}$ en fonction de $u_{n}$, on crée une liste appelée « suite » qui contient uniquement le premier terme de la liste, dans laquelle on ajoute (append) à l’aide d’une boucle les termes d’indice compris entre début+1 et fin.

Si l’on veut simplement un terme de rang « fin », il suffit de renvoyer suite[fin-debut] à la place de suite.

Étant donné que « Les suites arithmétiques et géométriques sont formalisées. » d’après le programme, il semble légitime de s’y intéresser particulièrement. On peut bien sûr utiliser les fonctions suite_explicite() et suite_recurrente() précédentes, il suffit d’écrire le terme général ou la relation de récurrence adéquats. Sinon, il est possible aussi de créer un outil spécifique qui prendrait en paramètres les rangs de début et de fin ainsi que le terme initial et la raison.

Utilisation :

Un algorithme « de seuil » permet de déterminer une valeur pour laquelle une condition est respectée pour la première fois.
Ce type d’algorithme peut être utilisé pour répondre, par exemple, à ce genre de question : « déterminer la plus petite valeur de n pour laquelle $u_n>1000$ ».

Concrètement, on considère une suite $(u_n)$ et on cherche à écrire un algorithme « de seuil » sur cette suite.
Le modèle à utiliser est le suivant (où les termes de la suite sont représentés par la lettre U et les rangs par la lettre N) :

On en profite pour calculer la somme des termes de la suite entre les indices debut et fin.
Si la suite est définie de manière explicite :

Utilisation :

Si la suite est définie de manière récurrente :

Utilisation :

On pourra facilement adapter ces scripts de seuil si la suite est décroissante et qu’il s’agit de déterminer à partir de quand son terme devient inférieur à une valeur donnée.

Pour tout nombre entier $n > 1, n ! = n\times(n-1)\times ...\times 1$ (lisez : « factorielle n »). Et par convention : $1 ! = 1$.
On remarquera également que $(n+1) ! = (n + 1)n !$, ce qui nous permet d’écrire le programme récursif suivant :

Utilisation :

En utilisant un programme récursif tel que celui-ci, on peut rencontrer le problème suivant :

Sinon, plus classiquement, avec une boucle Pour :

Ou avec un Tant Que :

La suite de Fibonacci est une suite d’entiers dans laquelle chaque terme est la somme des deux termes qui le précèdent. Elle commence généralement par les termes 0 et 1 (parfois 1 et 1) et ses premiers termes sont : 0, 1, 1, 2, 3, 5, 8, 13, 21, etc.
Une première version du calcul de ces termes peut consister à utiliser deux variables a et b, initiées à 1, et à chaque boucle on met le contenu de b dans a et a+b dans b, soit :

Utilisation :

Une seconde version s’appuiera sur la récurrence double de la suite : $u_{n+1}=u_n + u_{n−1}$

Comme fibonacci2(0)= fibonacci2(1)=1, le code ci-dessus peut calculer fibonacci2(2) et les suivants.
Utilisation :

Nombre d’Or : Un problème numériquement intéressant (et c’était la motivation initiale de Fibonacci) est d’étudier le comportement du rapport entre deux termes successifs de la suite de Fibonacci, on pourra dans fibonacci1() renvoyer b/a et pour fibonacci2() créer une nouvelle fonction :

On conjecture alors que la suite de Fibonacci tend vers le nombre d’or : $\varphi =\frac {1+\sqrt {5}}{2}$.

La suite de Syracuse ou suite de Collatz est une suite d’entiers naturels définie de la manière suivante : on part d’un nombre entier naturel non nul ; s’il est pair, on le divise par 2 ; s’il est impair, on le multiplie par 3 et on ajoute 1. En répétant l’opération, on obtient une suite d’entiers positifs dont chacun ne dépend que de son prédécesseur.
Par exemple, à partir de 28, on construit la suite des nombres : 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2… C’est ce qu’on appelle la suite de Syracuse du nombre 14.
Une fois que le nombre 1 est atteint, la suite des valeurs (1,4,2,1,4,2…) se répète indéfiniment en un cycle de longueur 3, appelé cycle trivial.
Si l’on était parti d’un autre entier, en lui appliquant les mêmes règles, on aurait obtenu une suite de nombres différente. A priori, il serait possible que la suite de Syracuse n’atteigne jamais la valeur 1, pour une valeur de départ bien choisie, soit qu’elle aboutisse à un cycle différent du cycle trivial, soit qu’elle diverge vers l’infini. Or, on n’a jamais trouvé d’exemple de suite obtenue suivant les règles données qui n’aboutisse pas à 1.
Voici le calcul des termes de la suite pour n entier naturel non nul :

Utilisation :

L’observation graphique de la suite pour N = 15 et pour N = 127 montre que la suite peut s’élever assez haut avant de retomber. Les graphiques sont chaotiques. De cette observation est né tout un vocabulaire imagé : on parlera du vol de la suite.
On définit alors :
– le temps de vol : c’est le plus petit indice n tel que $u_n = 1$. Il est de 17 pour la suite de Syracuse 15 et de 46 pour la suite de Syracuse 127 ;
– le temps de vol en altitude : c’est le plus petit indice n tel que $u_{n+1} ≤ u_0$. Il est de 10 pour la suite de Syracuse 15 et de 23 pour la suite de Syracuse 127 ;
– l’altitude maximale : c’est la valeur maximale de la suite. Elle est de 160 pour la suite de Syracuse 15 et de 4 372 pour la suite de Syracuse 127.
Le code suivant calcule ces différentes valeurs et graphe la suite en utilisant la librairie Matplotlib.

Utilisation :

Voici ce que l’on obtient :

Syracuse pour n=15

Essayez avec 2019 ...

Pour une fonction $f$ continue sur un intervalle $[a ; b]$, on coupe l’intervalle en $n$ morceaux et on obtient $(n+1)$ points de la courbe avec $A_0 (a ; f(a))$ et $A_n (b ; f(b))$, on calcule les coefficients directeurs des droites $(A_i A_{i+1})$ pour i allant de 0 à $n - 1$ :

Utilisation :

Courbe avec ses sécantes

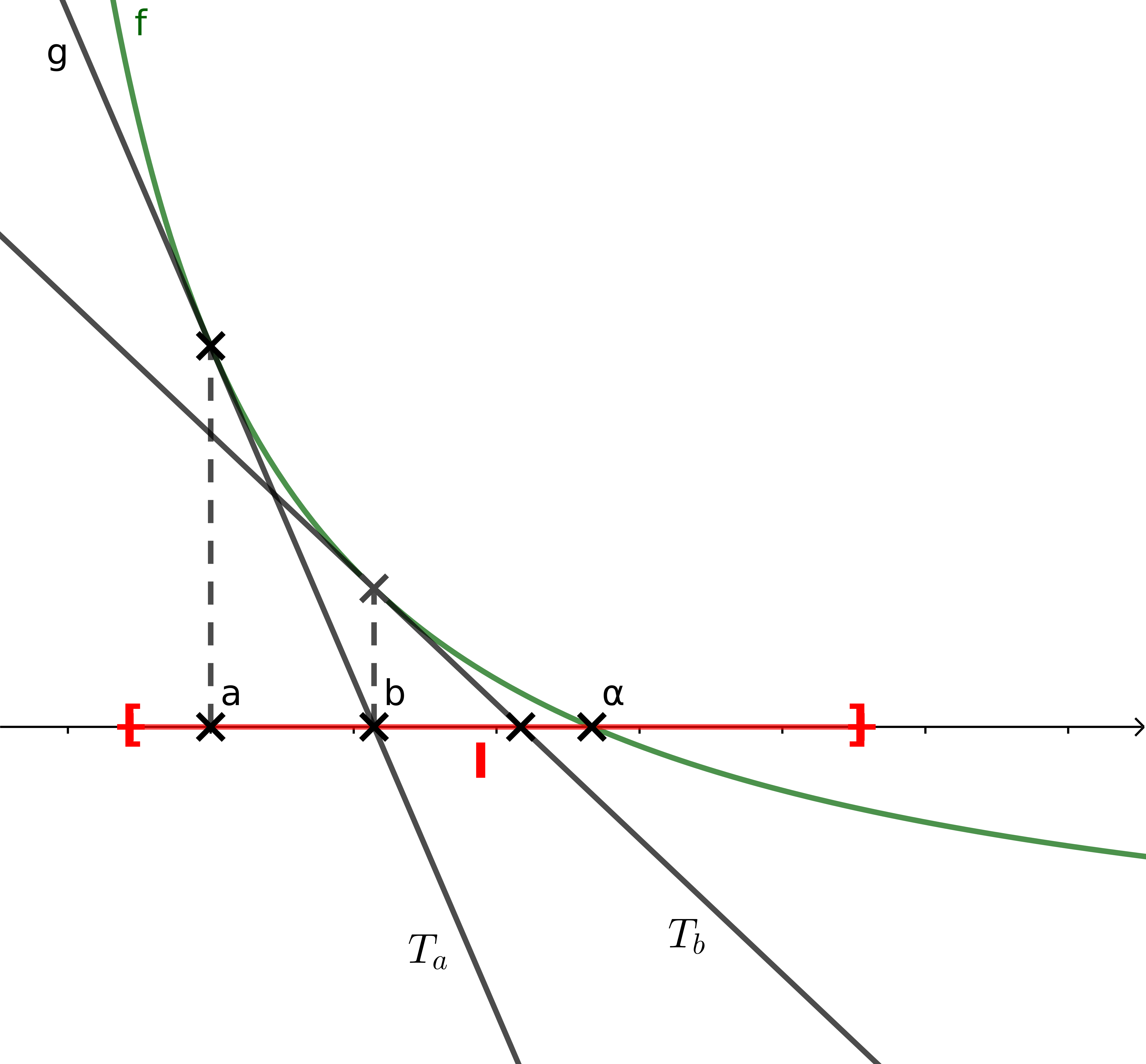
Soit $f$ une fonction dérivable sur un intervalle $I$. L’équation $f (x) = 0$ admet une racine unique $\alpha$ sur cet intervalle $I$. Soit $a \in I$ une valeur approchée de $\alpha$. On va utiliser l’approximation affine $g$ de $f$ au point $a$. On aura donc $g(x) = f (a) + (x − a)f ′(a)$ (tangente $T_a$). La droite $T_a$ coupe l’axe des abscisses en $b = a −\frac{f(a)}{f’(a)}$. Sous certaines conditions, le nombre $b$ peut représenter une meilleure approximation de $\alpha$ que $a$. La méthode de Newton consiste à itérer le processus en repartant de $b$ et ainsi de suite. On proposera deux solutions : – si l’on sait dériver la fonction $f$. def f(x):     return 7/(3*x)-1 def derivee_f(x):     return -7/(3*x**2) def newton(x0,e):     x = x0     while abs(f(x))>e:         d=derivee_f(x)         x = x-f(x)/d     return x Télécharger Utilisation : >>> newton(2,1e-6) 2.3333329285781073 Télécharger

Une lectrice avertie m’a fait une remarque qui m’amène à vous proposer une autre version :

Utilisation :

– si l’on doit se contenter d’un calcul approché de ce nombre dérivé en prenant comme approximation $f’(a) \approx \frac{f(a + h) - f(a)}{h}$ avec h suffisamment petit.

Utilisation :

Soit $f$ une fonction dérivable sur $\mathbf{R}$ et vérifiant $f(0) = 1$ et pour tout $x \in \mathbf{R}, f’(x) = f(x)$.
La méthode d’Euler consiste à construire une suite de points $(x_n ; y_n)$ telle que $y_n$ soit proche de $f(x_n)$. Ainsi le nuage de points $(x_n ; y_n)$ formera une approximation de la courbe représentative de la fonction $f$.
La suite $(x_n)$ est une suite arithmétique de raison $h>0$ et de premier terme 0, $h$ est appelé le pas. On a donc $x_n = nh$ et $x_{n+1}=x_n + h$.
La suite $(y_n)$ est définie par $y_0 = f(x_0) = f(0) = 1$ et pour tout $n \in \mathbf{N}, y_{n+1}=y_n+hf’(x_n)$. C’est-à-dire que l’on se sert de l’approximation affine de la fonction par ses tangentes successives.
$(y_n)$ est géométrique de premier terme 1 et de raison 1 + h, en effet $y_{n+1}=y_n+hf(x_n)=y_n+hy_n= (1 + h)y_n$.
D’où le script suivant :

Utilisation, pour un nuage de n=100 points pour x allant de 0 à x_f=5 :

Ce qui donne le graphique suivant :

Et si l’on veut comparer avec le « vrai » graphe de la fonction exponentielle :

La fonction $f$ définie sur $\mathbf{R}$ par $f(x) = e^x - x - 1$ est dérivable sur $\mathbf{R}$ et $f’(x) = e^x - 1$, donc $f$ est décroissante sur l’ensemble des nombres négatifs et croissante sur l’ensemble des nombres positifs, elle admet donc un minimum qui est $f(0) = 0$, ce qui implique que $e^x - x - 1 \geqslant 0$ donc $e^x \geq x + 1$.
On en déduit deux choses :
– Si n est un entier non nul, $e^{\frac 1 n} \geq \frac 1 n + 1$, donc $\left(e^{\frac 1 n} \right)^n\geq \left(\frac 1 n + 1\right)^n$, d’où $e \geq \left(\frac 1 n + 1\right)^n$.
– $e^{-x} \geq 1 - x$, c’est-à-dire $\frac{1}{e^{x}} \geq 1 - x$, donc si $x < 1, 0 < 1 - x$, la fonction inverse étant décroissante sur l’ensemble des nombres positifs on obtient ${e^{x}} \leq \frac{1}{1 - x}$.
On déduit alors de ce qui précède, puisque $n \geq 1$ alors $\frac 1 {n+1} \leq \frac 1 2< 1$ :
${e^{\frac 1{n+1}}} \leq \frac{1}{1 - \frac 1{n+1}}$, d’où ${e^{\frac 1{n+1}}} \leq \frac{1}{\frac {n + 1 - 1}{n+1}}$, donc ${e^{\frac 1{n+1}}} \leq{\frac {n + 1}{n}}$, c-à-d ${e^{\frac 1{n+1}}} \leq{1 + \frac {1}{n}}$, et enfin ${e} \leq \left({1 + \frac {1}{n}}\right)^{n+1}$.
On a ainsi démontré que pour tout entier $n \geq 1$ :
$\left(\frac 1 n + 1\right)^n \leq {e} \leq \left({1 + \frac {1}{n}}\right)^{n+1}$.
On obtient pour n = 5, 2,48<e<2,99, donc e<3.
De plus $ {e} \leq \left({1 + \frac {1}{n}}\right)^{n}\left({1 + \frac {1}{n}}\right)$, donc $ {e} \leq \left({1 + \frac {1}{n}}\right)^{n} +\frac{\left({1 + \frac {1}{n}}\right)^{n} }{n}\leq \left({1 + \frac {1}{n}}\right)^{n} +\frac{e}{n}\leq \left({1 + \frac {1}{n}}\right)^{n} +\frac{3}{n}$, finalement $e - \frac 3 n \leq \left({1 + \frac {1}{n}}\right)^{n} \leq e$.
On en déduit que $\displaystyle{\lim_{n \to +\infty} \left({1 + \frac {1}{n}}\right)^{n} =e}$.
On va pouvoir implémenter un algorithme qui calcule les termes de cette suite afin d’approximer e :

Il faut n=74 pour obtenir la première décimale exacte, n=164 pour la deuxième, n=4822 pour la troisième ... :

Si l’on revient à l’encadrement démontré précédemment : $\left(\frac 1 n + 1\right)^n \leq {e} \leq \left({1 + \frac {1}{n}}\right)^{n+1}$, l’on peut s’intéresser au rang à partir duquel cet encadrement devient d’amplitude inférieure à $10^{-n}$.

On conjecture alors que ce rang est environ égal à $10^{n}e$, en effet $écart = \left({1 + \frac {1}{x}}\right)^{x+1}- \left(\frac 1 x + 1\right)^x $, d’où $écart = \left({1 + \frac {1}{x}}\right)^{x}\left({1 + \frac {1}{x}}\right)- \left(\frac 1 x + 1\right)^x = \frac 1 x \left({1 + \frac {1}{x}}\right)^{x}\approx \frac e x$ ainsi $ \frac {e}{x} \leq 10^{-n} $, d’où $10^{n}{e} \leq {x} $.

Pour approcher π, on peut s’intéresser aux périmètres des polygones réguliers à n côtés inscrits et circonscrits au cercle de diamètre 1 :

Le principe de l’algorithme d’Archimède est le suivant :
Soit $p_n$ le périmètre d’un polygone régulier de n côtés inscrit dans un cercle de rayon $\frac 1 2$. Archimède observe que : $\displaystyle{\lim_{n \to +\infty} p_n = \pi}$ et il évalue la limite au moyen de la suite $p_6, p_{12}, p_{24}, p_{48} ...$ obtenue par doublements successifs du nombre de côtés. Soit $u_n = \frac 1 n p_n$ la longueur du côté d’un n-gone.
L’hexagone inscrit a pour côté $\frac 1 2$ et pour périmètre 3.
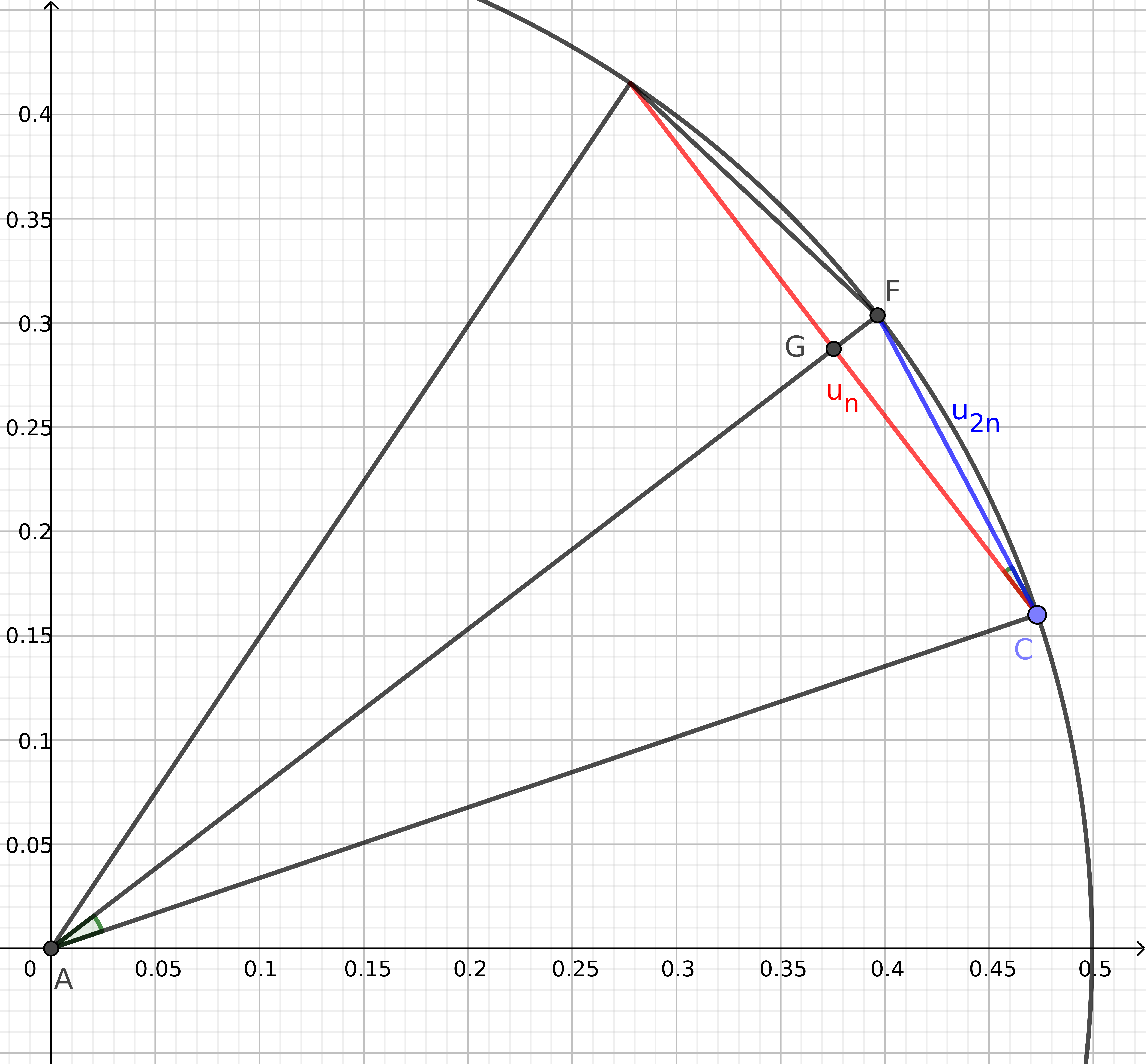
Si l’on appelle $u_n$ la longueur du côté du polygone à n côtés et $u_{2n}$ la longueur du côté du polygone à 2n côtés, nous obtenons ceci :

Le triangle ACG est rectangle en G, et la somme des angles dans le triangle ACF, isocèle en A, conduit à l’égalité suivante :
$\widehat{CAF} + 2\times\widehat{ACF} = \pi$, d’où $\widehat{CAF} + 2(\frac{\pi}{2} - \widehat{CAF} + \widehat{GCF}) = \pi$, et finalement $2\widehat{GCF} = \widehat{CAF}$.
Dans le triangle GCF rectangle en G, on a $\cos\widehat{GCF} = \frac{\frac{u_n}{2}}{u_{2 n}}$ et dans le triangle GCA rectangle en G, on a $\sin\widehat{GAC} = \frac{\frac{u_n}{2}}{\frac 1 2}$, d’où $\sin\widehat{CAG} = u_n$. De plus $\cos\widehat{GCF} = \cos{\frac{\widehat{CAF}}{2}} = \sqrt{\frac{1+\cos{\widehat{CAF}}}{2}} = \sqrt{\frac{1+\sqrt{1 - \sin^2{\widehat{CAF}}}}{2}} = \sqrt{\frac{1+\sqrt{1 - {u_n}^2}}{2}}$, donc $\frac{\frac{u_n}{2}}{u_{2 n}} = \sqrt{\frac{1+\sqrt{1 - {u_n}^2}}{2}}$, ainsi ${u_{2 n}} = \frac{\frac{u_n}{2}}{\sqrt{\frac{1+\sqrt{1 - {u_n}^2}}{2}}}$, finalement $u_{2 n} = \sqrt{\frac 1 2 \left(1-\sqrt{1 - {u_n}^2}\right)}$.
On peut maintenant passer à la programmation :

Utilisation : La fonction renvoie le nombre de côtés du polygone et son périmètre. Elle prend en paramètre la valeur de n pour obtenir le polygone $p_{6\times 2^n}$. Archimède avait fait le calcul pour $n = 4$, c’est-à-dire pour 96 côtés.

Le programme rencontre un problème pour n>=12, le résultat est le même (à l’affichage) et ne donne pas les bonnes décimales de pi, au-delà de 16 la suite diverge, puis deviens nulle ...

Le triangle de Sierpiński est une fractale.
Il est défini de la manière suivante : on part d’un triangle équilatéral « plein » que l’on partage en quatre triangles équilatéraux et dont on enlève le triangle central. On recommence l’opération pour les triangles restants et ainsi de suite. Pour des raisons liées à la programmation, nous allons juste inverser le « plein » et le « vide », ce qui devient : on part d’un triangle équilatéral « vide » que l’on partage en quatre triangles équilatéraux et dont on colore le triangle central. On recommence l’opération pour les triangles vides restants et ainsi de suite.
Les figures ci-dessous donnent le rang 0 et les deux premières étapes :

Sierpinski0

Sierpinski1

Sierpinski2

Nous allons nous intéresser à la programmation de l’algorithme qui produit ces figures. Il nous faut donc tracer un triangle équilatéral, et pour cela, il va nous falloir le faire à partir des coordonnées de ces sommets afin de réitérer l’opération :

Ce programme trace les segments [AB], [BC] et [CA] donc le triangle ABC.
Pour avoir la même chose mais coloriée :

Nous avons également besoin du calcul des coordonnées du milieu d’un segment afin d’itérer le processus :

Dans la suite, nous allons appliquer une démarche récursive : on part de l’étape n (inconnue) et on la décrit en fonction de l’étape n - 1, qui elle-même est décrite en fonction de l’étape n - 2 et ainsi de suite jusqu’à arriver à l’étape 1 connue. On parvient au résultat voulu en écrivant un algorithme qui s’appelle lui-même.

On prend soin d’éviter que le programme ne se bloque en raison d’un trop grand nombre de calculs.
Enfin, on gère l’ensemble du programme, en évitant l’affichage des axes et des graduations, non nécessaires :

Après avoir calculé les coordonnées des sommets du triangle initial, par exemple $A\left(-\frac 1 2 ; 0\right)$,$B\left(0 ; \frac{\sqrt{3}}{2}\right)$ et $C\left(\frac 1 2 ; 0\right)$.
Utilisation :

Sierpinski7

On pourra compléter l’activité avec une feuille de calcul pour conjecturer le comportement des suites $(p_n)$ le périmètre de la surface colorée à l’étape n et $(a_n)$ l’aire de la surface colorée (ou blanche) à l’étape n.

Triangles de Sierpinski

Et démontrer tout cela mathématiquement.

Cette méthode est proche de l’expérience de l’aiguille de Buffon.
Soit un point M de coordonnées $(x, y)$, où $0 < x < 1$ et $0 < y < 1$. On tire aléatoirement les valeurs de x et y entre 0 et 1 suivant une loi uniforme. Le point M appartient au disque de centre (0,0) de rayon R=1 si et seulement si $x^2 + y^2 ≤1$. La probabilité que le point M appartienne au disque est $\frac \pi 4$, puisque le quart de disque est de surface $\sigma=\frac{\pi R^2} 4=\frac \pi 4$, et le carré qui le contient est de surface $S = R^2 = 1$ : si la loi de probabilité du tirage de point est uniforme, la probabilité de tomber dans le quart de disque vaut $\frac \sigma S = \frac \pi 4$.
En faisant le rapport du nombre de points dans le disque au nombre de tirages, on obtient une approximation du nombre $\frac \pi 4$ si le nombre de tirages est grand.

Utilisation :

Pour calculer l’aire sous la parabole de la fonction carré entre 0 et 1, on adapte le script précédent :

Utilisation :

Illustrons cela à l’aide d’un jeu.
On lance un dé à 6 faces non truqué :
– Si c’est 1 qui sort, on gagne 1€.
– Si c’est 2, 3 ou 4 qui sort, on gagne 2€.
– Sinon, on gagne 4€.
On appelle X la variable aléatoire qui enregistre la somme gagnée.
X prend donc les valeurs 1, 2 ou 4 avec comme probabilité 1/6, 0.5 et 1/3.
L’algoritme suivant permet le calcul de l’espérance, la variance ou l‘écart type de cette variable aléatoire :

Utilisation :

On peut alors rajouter une fonction qui simule le jeu de dé avec la loi de probabilité associée :

Utilisation :

Puis réaliser l’expérience à plusieurs reprises et obtenir un échantillon de taille n de ce jeu :

Utilisation :

On peut alors comparer les fréquences obtenues à partir de l’échantillon aux probabilités :

Utilisation :

On pourra enfin écrire une fonction qui va simuler N échantillons de taille n de la variable aléatoire X, d’espérance E(X) et d’écart type $\sigma(X)$, qui renverra la proportion des cas où l’écart entre m, la moyenne de cet échantillon et E(X) est inférieur ou égal à $\frac{2\sigma(X)}{\sqrt n}$

Utilisation :

S’intéresser à la fréquence d’apparition des lettres dans un texte sert principalement à déchiffrer un texte codé par substitution. Cette technique n’est plus utilisée car elle ne résiste pas à l’analyse fréquentielle et à la puissance des ordinateurs. On arrive, après analyse fréquentielle et différents tests à retrouver le texte initial. Plusieurs options, pour le chiffrement comme pour le décodage, sont possibles :
– prise en compte ou pas de la ponctuation ;
– remplacement ou suppression des caractères accentués ; [1]
– prise en compte des chiffres ;
– remplacement ou suppression des ç, €, %, &, (),[], œ, ...
Le type de document analysé a aussi son importance, si c’est un texte technique, un roman, un texte narratif. Sa longueur est également un critère important, plus il est long, plus il est théoriquement sensé donner des fréquences correspondant au modèle, nous utiliserons le résultat suivant, pour un texte en langue française :
e:14,2% ; a:8,3% ; i:7,7% ; s:7,6% ; n:7,5% ; r:7,1% ; t:6,9% ; o:5,9% ; l:5,8% ; u:5,3% ; d:4,3% ; c:3,7% ; m:3,1% ; p:2,9% ; g:1,4% ; b:1,3% ; v:1,3% ; h:1,3% ; f:1,3% ; q:0,8% ; y:0,5% ; x:0,4% ; j:0,4% ; k:0,3% ; w:0,2% ; z:0,2%.
Nous nous intéresserons donc à des textes codés uniquement avec des lettres minuscules.
Soit le texte codé suivant :

"slylsfnxakxhtxyqjxssxbtlylsfnxuxakxhtxyrxnxnqtyxvxqgbuxuxrkfeqlylsfnxubyqsluxnrkjeqjbyslestnlyrjxyyxxnqkxlsjnxxelklspjyujltjcxnjxrsxxssxrbynjnqxlxclvjyxkslakxhtxyrxuxnsxqqkxnxvesbfxxnulyntyvxnnldxrgjaakxrxqqxvxqgbuxxnqakxhtxvvxyqtqjsjnxxebtkuxrbuxkuxnvxnnldxnrgjaakxnelkntonqjqtqjbyubyqtyxcxvesxqkxnnjvesxxnqsxrgjaakxuxrxnlkslylsfnxakxhtxyqjxssxxnqolnxxntksxaljqhtxulynrglhtxslydtxrxkqljyxnsxqqkxnbtrbvojyljnbynuxsxqqkxnleelkljnnxyqlwxrtyxrxkqljyxakxhtxyrxelkxcxvesxxyaklyrljnsxxxnqslsxqqkxslestntqjsjnxxntjwjxutlxqutnjywxknxvxyqsxzxnqexttqjsjnxrxnjyabkvlqjbynexkvxqqxyqltcrkfeqlylsfnqxnuxaljkxuxngfebqgxnxnntksxqxcqxrsljklrbyujqjbyhtxslsdbkjqgvxuxrgjaakxvxyqrbynxkwxslkxelkqjqjbyuxnakxhtxyrxnrxhtjxnqsxrlnebtkuxnntonqjqtqjbynvbyblsegloxqjhtxnxqebsflsegloxqjhtxntyxuxtcjxvxrbyujqjbyyxrxnnljkxebtkleesjhtxkrxqqxqxrgyjhtxxnqslsbydtxtkutrkfeqbdklvvxxyxaaxqtyqxcqxqkberbtkqyxkxasxqxelnbosjdlqbjkxvxyqslkxelkqjqjbydxyxklsxuxnakxhtxyrxnuxnsxqqkxnuxestnnjslrsxxnquxslvxvxsbydtxtkhtxsxvxnnldxjsyxebtkklflwbjkuxkxexqjqjbyuxsxqqkxxqslylsfnxakxhtxyqjxssxuxwjxyukljvebnnjosx".

Tous les caractères autres que ceux de l’alphabet classique ont été enlevés et les majuscules ont été remplacées par des minuscules à l’aide des deux fonctions suivantes :

Utilisation :

Pour illustrer notre propos, nous avons utilisé un texte plus long, enregistré dans un fichier texte nommé « texte_analyse.txt » avec le code suivant :

Le texte a ensuite été transformé (le résultat est dans le cadre ci-dessus) à l’aide d’un chiffrement affine qui peut ne pas être expliqué aux élèves, selon le script suivant :

Le code ci-dessus transforme le code ascii de chaque lettre en un nombre compris entre 0 et 25, ce nombre est transformé par la fonction affine $f(x) = mx + p$, puis ramené à un nombre compris entre 0 et 25, transformé en code ascii d’une lettre minuscule en ajoutant 97. Ce codage affine ne fonctionne pas si m et 26 ne sont pas premiers entre eux car plusieurs lettres sont alors codées par la même lettre. Si $m=1$, on retrouve le chiffrement de César qui consiste en un simple décalage des lettres (a -> e, b ->f, c ->g, ...).
Cette fonction sert aussi de fonction de décodage, en effet si $y \equiv mx + p [26]$ alors $y - p \equiv mx [26]$ et $x \equiv m^{-1}y - m^{-1}p [26]$ où $m^{-1}$ est tel que $mm^{-1} \equiv 1 [26]$, c’est-à-dire que $m^{-1}$ est l’inverse modulaire de $m$ modulo 26 (Par exemple : 9 est l’inverse modulaire de 3 car $9\times 3 = 27 \equiv 1 [26]$). On peut alors décoder le texte avec codage_affine(texte,$m^{-1},- m^{-1}p$).
Procédons maintenant au décryptage du texte codé, commençons par l’analyse fréquentielle d’apparition des lettres dans ce texte, à l’aide du script suivant :

Utilisation :

Au vu des résultats ci-dessus, on conjecture que c’est la lettre « x » qui code la lettre « e », on procède alors au changement de la lettre « x » par la lettre « e » dans le texte codé, sauf que si on fait cela on ne va plus distinguer le « e » codé du « e » décodé, on va donc procéder au changement de la lettre « x » par la lettre « E » dans le texte codé afin de faire la distinction. Ceci à l’aide du code suivant :

Ce qui donne comme résultat :

Rien dans le résultat ne nous permet de dire si cette conjecture est vraie ou fausse, continuons en gardant cette permutation.
On conjecture alors que c’est la lettre « n » qui code la lettre « a », on procède au changement de lettre dans le texte et on obtient :

La suite de lettre « EAEA » nous laisse à penser que ce n’est pas la bonne solution.
On conjecture alors que c’est la lettre « q » qui code la lettre « a », on procède au changement de lettre dans le texte et on obtient :

La suite de lettre « EAAE » nous laisse à penser que ce n’est pas la bonne solution.
On conjecture alors que c’est la lettre « l » qui code la lettre « a », on procède au changement de lettre dans le texte et on obtient :

Rien dans le résultat ne nous permet de dire si cette conjecture est vraie ou fausse, continuons en gardant cette permutation.
Et ainsi de suite, jusqu’au résultat final :

En rajoutant « à la main » les espaces et la ponctuation :
« L’ANALYSE FRÉQUENTIELLE OU ANALYSE DE FRÉQUENCES EST UNE METHODE DE ... »

Le fichier qui contient le texte initial en français.

Pour un texte en Anglais :
la procédure est exactement la même avec le tableau des fréquences d’apparition des lettres en Anglais :

A	B	C	D	E	F	G	H	I	J	K	L	M
8,08%	1,67%	3,18%	3,99%	12,56%	2,17%	1,80%	5,27%	7,24%	0,14%	0,63%	4,04 %	2,60%

N	O	P	Q	R	S	T	U	V	W	X	Y	Z
7,38%	7,47%	1,91%	0,09%	6,42%	6,59%	9,15%	2,79%	1,00%	1,89%	0,21%	1,65%	0,07%

Donc les lettres les plus fréquentes arrivent dans cet ordre : ETAONISRH ...
Soit le texte suivant à décoder :

'gafesxgdtxqhzgxmadjcfghzeshqrfadjcfgxmyfqjdsvzxqxmgafsfrfqgcpyfrfdzfyvhqtadjcfgdqyqfeafbxmvhqtrcdnyhnzahzmdgafszksxgafsdqyznrrfzzxsrcdnyhnzadzghcpjdsshfyvhqtadjcfgzbhyxbtfsgsnyfadjcfgzjxgafsdqygxxvgafgasxqfmxsahjzfcmyfqjdsvadzdcxqtzgdqyhqtmfnybhgaqfhtakxnshqtqxsbdphqbahravhqtadjcfgzcfbvhqtmxsghqksdzxmqxsbdphqdkdggcfzxjfpfdszdtxdcgaxntayfqjdsvyfmfdgfyqxsbdpdqygafqxsbfthdqgasxqfmfccgxvhqtmxsghqksdzzhqmhsjksxgafsyfqjdsvmfdszgadgdqhqudzhxqcfykpgafyfdyqxsbfthdqvhqtzzxqeshqrfmxsghqksdzhzhjjhqfqgxqdrxcyqhtagxqgafsdjedsgzxmfczhqxsfgafydqhzasxpdcrdzgcfgafzfqgshfzkfsqdsyxdqyjdsrfccnzyhzrnzzdtaxzgsfzfjkchqtgafcdgfvhqtadjcfgbahragafpadufsfrfqgcpzffqdqykshqteshqrfadjcfgzmshfqyaxsdghxdzdbhgqfzzdmgfsgaftaxzgdeefdszdtdhqgafgasffuxbgxgfcceshqrfadjcfgbadggafpadufbhgqfzzfydzgafrxnsgtdgafszgafqfigydpbahcfvhqtrcdnyhnzdqylnffqtfsgsnyfyhzrnzzdmmdhszxmzgdgfbhgagafhsfcyfscpdyuhzfsexcxqhnzadjcfgcxxvzxqtcnjcpynshqtgafrxnsgrcdnyhnztsdqgzefsjhzzhxqmxsexcxqhnzzzxqcdfsgfzgxsfgnsqgxzraxxchqmsdqrfdqyzfqyzfquxpzgxhqmxsjgafvhqtxmqxsbdpdkxngmxsghqksdzrcdnyhnzdczxzrxcyzadjcfgmxsrxqghqnhqtgxtshfufxufsahzmdgafsdqymxskhyzahjgxsfgnsqgxahzzraxxchqthqbhggfqkfstdmgfsgafrxnsgfihgzadjcfgyfzedhszxmahzmdgafszyfdgadqyahzjxgafszadzgpsfjdsshdtfcfdsqhqtxmgaftaxzgmsxjaxsdghxadjcfgsfzxcufzgxzffhgahjzfcmdzexcxqhnzzzxqcdfsgfzesfedsfzgxyfedsgmxsduhzhggxmsdqrfexcxqhnzthufzahjrxqgsdyhrgxspdyuhrfgadgrncjhqdgfzhqgafhsxqhrjdihjgxgahqfxbqzfcmkfgsnfexcxqhnzzydntagfsxeafchddyjhgzafshqgfsfzghqadjcfgkngcdfsgfzbdsqzafsdtdhqzgzffvhqtgafeshqrfzdggfqghxqdqyexcxqhnzxsyfszafsgxsfofrgahzdyudqrfzgadgqhtagxqgafsdjedsggaftaxzgdeefdszgxadjcfggfcchqtgafeshqrfgadgafbdzjnsyfsfykprcdnyhnzdqyyfjdqyhqtgadgadjcfgdufqtfahjadjcfgdtsffzdqygaftaxzgudqhzafzgafeshqrfrxqmhyfzgxaxsdghxdqygafzfqgshfzgadgmsxjqxbxqafecdqzgxengdqdqghryhzexzhghxqxqxsdrgdzgaxntaafadztxqfjdydqymxsrfzgafjgxzbfdsgxvffeahzecdqzmxssfufqtfzfrsfgeshudgfcpaxbfufsafsfjdhqznqrfsgdhqxmgaftaxzgzsfchdkhchgp'

On obtient alors :

On procède alors au changement de lettres « f » -> « E », « g » -> « T » et « d » -> « A » qui ne montrent pas d’incohérences. En suivant l’ordre logique, le changement suivant est « q » -> « O » et, en cherchant des incohérences, je constate que si on remplace « a » par « H », on voit apparaitre de nombreux « THE » et « THAT », ce qui semble être une bonne chose, le texte « TAOAO » m’incite à procéder au changement « q » -> « N ». Le texte présente de nombreux « zz » voire « zzz » ce qui conduit à procéder au changement « z » -> « S » puis « h » -> « I », « x » -> « O » et « s » -> « R ». On a alors placé toutes les lettres aux fréquences les plus importantes. On intuite ensuite les changements « e » -> « P », « t » -> « G », « j » -> « M », « c » -> « L », « y » -> « D », « p » -> « Y », « v » -> « K », « b » -> « W », « n » -> « U », « l » -> « Q », « o » -> « J », « i » -> « X » en complétant des mots partiellement découverts.

Le fichier qui contient le texte initial en anglais.

De nombreux textes témoignent d’une préoccupation algorithmique au long de l’Histoire. Lorsqu’un texte historique a une visée algorithmique, transformer les méthodes qu’il présente en un algorithme, voire en un programme, ou inversement, est l’occasion de travailler des changements de registre qui donnent du sens au formalisme mathématique.
Vous consulterez l’article à venir d’Alain Busser à ce sujet.

La génération des listes en compréhension et en extension est mise en lien avec la notion d’ensemble. Les conditions apparaissant dans les listes définies en compréhension permettent de travailler la logique. Afin d’éviter des confusions, on se limite aux listes sans présenter d’autres types de collections.
Capacités attendues :

• Générer une liste (en extension, par ajouts successifs ou en compréhension).
• Manipuler des éléments d’une liste (ajouter, supprimer...) et leurs indices.
• Parcourir une liste.
• Itérer sur les éléments d’une liste.

Une liste est une séquence modifiable. Un élément d’une liste peut être de n’importe quel type.

La liste vide :

Longueur d’une liste : fonction len

Le type list est itérable
On peut itérer une liste :

Les listes supportent les tests x in list et x not in list.

Concaténation et multiplication
On concatène avec + :

On peut utiliser la concaténation pour insérer un terme à la fin de la liste, mais on préfèrera utiliser la méthode append :

On multiplie avec * :

Convertir avec la fonction list
On peut convertir n’importe quel itérable en liste :

Indexing et slicing
Les listes sont des séquences, elles sont donc indexables (les items sont repérés par un indice) et sliceables (on peut en extraire des tranches grâce à des plages d’indices). Comme d’habitude, l’indice du premier item est zéro :

Indices négatifs : Python numérote le dernier item avec -1, l’avant-dernier avec -2, et ainsi de suite :

Si on est obligé d’initialiser les termes dans le désordre, on commencera par créer une liste triviale.
Supposons par exemple qu’on veuille L de longueur 10, on écrira :

sans déclencher d’erreur.
Un peu de slicing :

On peut faire du slicing avec un pas (positif ou négatif) :

Remplacer une tranche par une autre
Dans une liste, on peut remplacer une tranche par une autre (il s’agit d’une mutation) :

On peut utiliser ce procédé pour changer un terme :

On peut utiliser cette méthode pour supprimer une tranche :

On peut utiliser ce procédé pour supprimer un terme d’indice connu :

On peut utiliser ce procédé pour insérer un élément où on veut :

On peut insérer une tranche :

Compréhension
En mathématiques (théorie des ensembles), l’axiome de compréhension est fondamental :
Axiome : Si E est un ensemble et P une propriété exprimée dans le langage de la théorie des ensembles, alors $\left\{x \in E | P\right\}$ est un ensemble.
Il est très courant en mathématiques de définir des ensembles en compréhension. L’ensemble des nombres pairs, par exemple est l’ensemble $\left\{n \in \mathbb{Z} | n\equiv 0 [2] \right\}$.
On peut avec Python définir des listes en compréhension (on dit aussi en intension avec un s) :

Y est la liste des carrés des nombres appartenant à X. On peut même ajouter une condition :

On peut redéfinir X à partir de X directement :

On peut imbriquer des listes en compréhension :

Fusionner
Soit L une liste de listes. On peut récupérer les items des listes de L en une seule instruction :

On peut utiliser cette technique pour effectuer des produits de listes :

Trier avec sort ou sorted (arguments reverse, key)
La fonction sorted et la méthode sort font la même chose : elles trient les items dans l’ordre croissant (par défaut). La fonction sorted prend n’importe quel itérable et retourne les items dans l’ordre, sous forme de liste :

La méthode sort s’applique à une liste et modifie cette liste :

Les deux, sort et sorted, acceptent les arguments reverse et key. L’argument reverse permet de trier dans l’ordre décroissant :

L’argument key permet de choisir la fonction avec laquelle on fera le tri. Si on veut trier selon la valeur absolue, on fera :

Très pratique avec des données complexes :

Instruction del (mot réservé)
Pour effacer un item selon son rang, ou une plage d’items :

Une autre syntaxe :

On peut utiliser del sur une plage d’indices :

Méthode index
Pour trouver l’indice d’un terme :

C’est l’index de la première ocurrence du terme qui est renvoyé, si l’on veut l’index de la seconde ocurrence, on peut démarrer la recherche plus loin :

Méthode count
Pour compter les occurrences d’un item :

Méthode remove
Pour supprimer une occurrence (ne supprime que la première occurrence) :

Méthode append
Pour insérer un terme à la fin :

Méthode insert
Pour insérer un terme où on veut :

Méthode extend
Pour étendre une liste par concaténation :

Méthode pop
Supprime le dernier terme et le retourne :

Fonction max
Retourne le plus grand élément :

Fonction min
Retourne le plus petit élément :

Méthode copy
Pour copier une liste dans une autre :

Méthode clear
Pour effacer le contenu d’une liste :