On considère la fonction f telle que

• f(x)=2-x² si x<1 ;
• f(x)=x²-3 sinon.

Le problème est de la représenter graphiquement...

L’intérêt de ce genre de fonction, en Seconde, est algorithmique, ou ici, algébrique : La notion de test y est ici mise en œuvre, et en plus c’est un test simple : Comparaison entre x et 1. Avec CaRMetal cela s’écrit

La représentation graphique de cette fonction pose problème :

Une solution à ce problème est de représenter graphiquement non une fonction, mais deux : Deux morceaux de parabole. Ici f1 (en bleu) est la fonction 2-x*x avec Xmax=1, et f2 (en vert) est la fonction x*x-3 avec Xmin=1 :

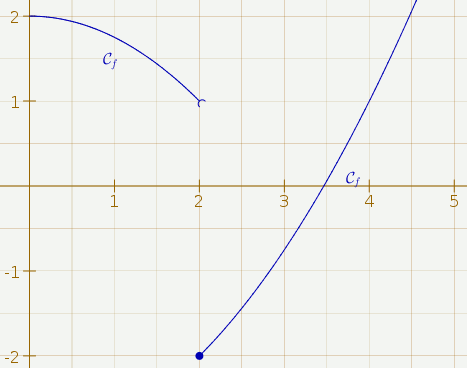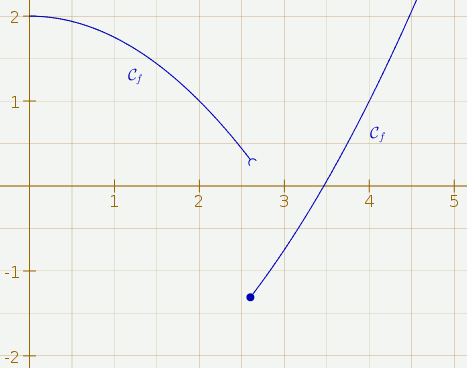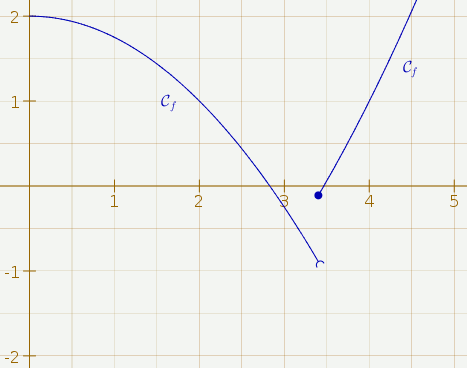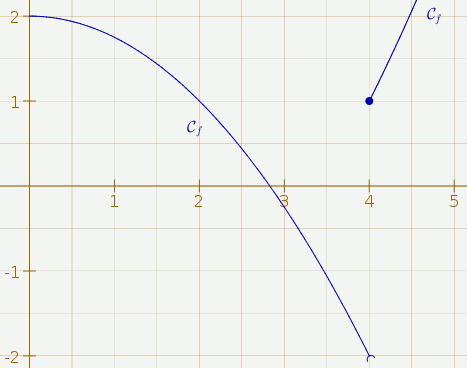
Il subsiste encore un problème : On ne voit pas sur la figure l’image de 1 lui-même. Or depuis la version 3.7.8, CaRMetal permet de coder le caractère ouvert ou fermé de la courbe. Pour fermer f2 à gauche, on clique sur l’icône représentant un point :

L’aspect du bouton change légèrement pour signaler que maintenant, la fonction est « fermée » à gauche :

De même, l’autre fonction doit être ouverte en son maximum 1, ce qui se fait en cliquant sur l’outil d’ouverture du côté droit (puisque c’est le maximum de x) :

On a alors la représentation graphique souhaitée :

Par défaut, une fonction n’est ni ouverte, ni fermée ; et en cliquant à nouveau sur un bouton « enfoncé », on peut remettre la fonction dans cet état initial. De même, en fermant une fonction qui était ouverte, le bouton d’ouverture est désactivé.

Les composantes connexes du graphe doivent être (re)définies une par une, et le codage doit être fait (ou non, on n’est pas obligé...) pour chacune d’entre elles. Mais le résultat, exporté à un format graphique vectoriel puis inséré dans un document (traitement de texte ou LaTeX), sort sur une imprimante laser avec une haute qualité, et sans trop d’effort il est plus facile de cliquer sur des icônes que de programmer en LaTeX...).

La fonction qui, à x réel, associe sa partie entière [1], se note floor dans CaRMetal :

Sa représentation graphique montre pourquoi on appelle ce genre de fonction, une fonction en escalier :

Pour coder sur le graphique le fait que la partie entière de 3 est 3 et non 2, il faut représenter plusieurs fonctions sur des intervalles de la forme [n ;n+1], et pour cela, on utilise une boucle en JavaScript. Le script commence ainsi :

Pour se rappeler la syntaxe d’une représentation graphique en CaRScript, on clique sur l’icône correspondante :

Ce qui rappelle que l’on doit entrer les bornes de l’intervalle (ici n et n+1) et la valeur de la fonction (n à nouveau) :

Ce script produit la même figure que floor(x) ci-dessus, mais on peut coder aussi en JavaScript les ouvertures et fermetures de segments sur le graphique :

• SetMinOpen pour un demi-cercle à gauche ;
• SetMinClosed pour un point à gauche ;
• SetMaxOpen pour un demi-cercle à droite ;
• SetMaxClosed pour un point à droite.

Dans chaque cas, le booléen correspondant doit être positionné à true :

Ce script construit la représentation graphique « correcte » de la fonction partie entière :

En soustrayant à un nombre x sa partie entière floor(x), on obtient sa partie fractionnaire [2]. Cette fonction présente l’intérêt d’être périodique, et en plus, d’avoir une période plus simple que les fonctions trigonométriques : 1...

Pour la représenter avec le codage des discontinuités, on peut faire comme dans l’onglet précédent, avec ce CaRScript :

On obtient alors cette frise (ce qui montre bien qu’elle est 1-périodique) :

Si elle est 1-périodique, elle a une série de Fourier. Or il se trouve que celle-ci est relativement simple : Outre le terme constant qui est 1/2, les autres termes sont de la forme sin(2πnx)/(πn) ; ce qui permet de dire, en notant E(x) la partie entière de x :

La vidéo des sommes partielles de Fourier, de l’ordre 1 à l’ordre 16, montre que la vitesse de convergence est plus rapide au centre des segments qu’à leurs bords :

Le fichier au format CaRMetal, avec son curseur, est téléchargeable en bas d’article. Le fait que les approximations par sommes de Fourier se laissent emporter par leur élan à chaque saut, et dépassent la valeur à atteindre, est le phénomène de Gibbs, qu’on va illustrer sur un autre exemple dans les onglets suivants.

La fonction que voici a une série de Fourier plus simple (que des sinus) parce qu’elle est impaire :

La fonction sign de CaRMetal associe à un nombre réel, le nombre 1 s’il est positif et le nombre -1 s’il est négatif ; la fonction sign(rsin(pi*x)) est donc périodique de période 2 (rsin désigne le sinus en radians sous CaRMetal). Mais elle se dessine sous forme de segments :

D’après un théorème_de_Dirichlet_(séries_de_Fourier), la série de Fourier d’une fonction réglée tend vers la moyenne entre les limites à gauche et à droite de f(x). Si f est continue en x, cette moyenne vaut f(x) et la série converge. Donc si f est discontinue en 0, on a intérêt à poser que f(0)=(fg(0)+fd(0))/2 (fg(0) et fd(0) désignant les limites à gauche et à droite de f en 0).

La fonction f ci-dessus est discontinue en les nombres entiers. La moyenne de 1 et -1 valant 0, on pose f(n)=0 si n est entier. Pour le coder sur la représentation graphique, il faut donc rajouter des points de coordonnées (n ;0) pour tout n, et ouvrir tous les segments. Pour ce qui est de l’ouverture des segments, l’algorithme ci-dessous devrait convenir :

Le rendu est effectivement correct dans les nombres négatifs, mais pas dans les nombres positifs :

(aux coordonnées (2 ;-1) par exemple, on voit qu’il y a un problème).

Pour voir ce qui ne va pas, on peut changer de couleur la représentation graphique d’un des morceaux (ici, la fonction f12 qui vaut 1 pour x entre 2 et 3) :

Sur ce coup-là, CaRMetal a considéré que le signe de 0 était -1 et non 0 (une petite erreur d’approximation, amplifiée par la discontinuité). Ce qui suggère la remédiation suivante : Remplacer 2 par 2,001. Avec les points, créés et mis en gras à la volée, le script complet devient

Il produit l’effet suivant :

Pour illustrer le phénomène de Gibbs, on ajoute à cette représentation graphique, une somme partielle de la série de Fourier de f. Par exemple à l’ordre 7 :

La voici, en bleu, superposée à la représentation graphique de l’onglet précédent :

Pas terrible : L’algorithme de tracé de CaRMetal est rapide mais au prix d’une approximation polygonale un peu grossière. Pour y remédier, il suffit d’imposer un pas assez petit, par exemple 0,001 (trouvé empiriquement) :

L’affichage est nettement meilleur :

Pour avoir une somme de Fourier à un ordre plus grand, le mieux est de construire son expression algébrique avec un CaRScript ; l’algorithme peut se décrire ainsi :

• initialiser une chaîne de caractères avec le début de l’expression : 4/pi*(0
• faire une boucle sur l’indice n, allant de 1 à 7 par pas de 2 (par exemple), dans laquelle, pour chaque valeur de n, on ajoute un terme de la somme de Fourier : +rsin(_n*pi*x)
• après la boucle, refermer la parenthèse en ajoutant à la chaîne de caractères, ladite parenthèse : )

L’algorithme, en JavaScript et avec affichage de la chaîne pour vérification, s’écrit ainsi :

Puisque la chaîne de caractères obtenue a l’air correcte, on peut tranquillement remplacer le 7 par un 33 et créer une fonction ayant cette expression algébrique pour valeur :

pour avoir la somme d’ordre 33 :

sur laquelle le phénomène de Gibbs se constate mieux :

En production de documents, CaRMetal devient donc irremplaçable sur ce sujet. Mais c’est quand même avant tout un logiciel de géométrie dynamique, et dans l’exemple présent, il serait intéressant de pouvoir changer l’ordre de la série de Fourier par un curseur.

L’astuce [3] consiste à multiplier chaque terme par un booléen (en fait converti en entier), égal à 0 ou 1 selon que le terme doive être affiché ou non. Or c’est précisément le cas de N>5 qui est égal à 1 si le curseur N est suffisamment grand, et à 0 sinon. Donc, comme les termes à afficher sont de toute manière impairs, on multiplie le terme d’odre n par 2*N+1>n pour que sa visibilité soit dépendante du curseur comme souhaité :

L’allure de la courbe va alors de la simple sinusoïde à la figure précédente selon la valeur du curseur N. Le résultat est téléchargeable ci-dessous, mais si on l’ouvre avec une ancienne version de CaRMetal, l’affichage des fonctions en vert sera moins bien codé.

En actionnant le curseur, on voit l’évolution des oscillations, comme le montre cette vidéo :