Le jeu de l’ourson
Le jeu se joue sur ce graphe :
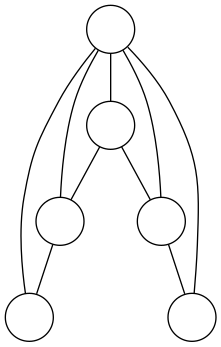
L’un des joueurs appelé Ourson dispose d’un pion de couleur rouge (par exemple) et l’autre dispose de deux pions bleus (les chiots) indiscernables l’un de l’autre. Au début du jeu, les pions sont disposés ainsi :
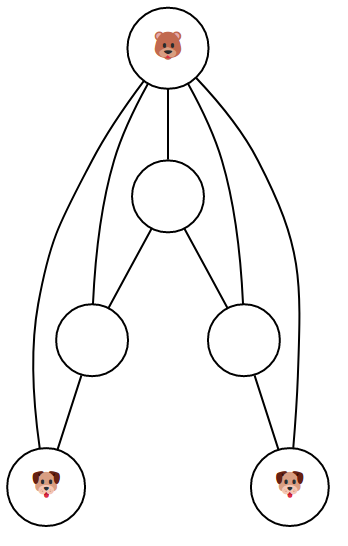
Quand c’est au tour des chiots de jouer, ils bougent un seul des pions bleus selon une arête du graphe, vers un sommet libre (ne comportant aucun pion). Quand c’est à l’ourson de jouer, il bouge son unique pion selon une arête du graphe, vers un sommet libre ... s’il le peut ! En effet le but du jeu pour les chiots est de bloquer l’ourson dans un coin, comme ici :
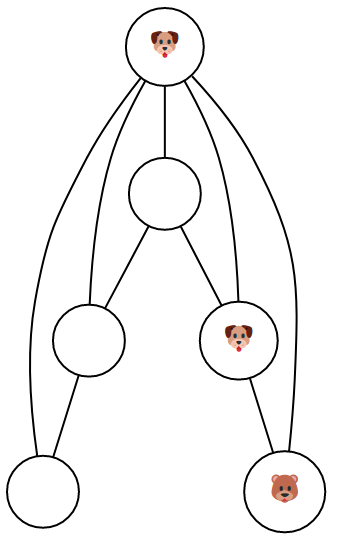
Dès que l’ourson est bloqué, les chiots ont gagné. Si au bout de 16 mouvements l’ourson n’est toujours pas bloqué, il a gagné. C’est l’ourson qui commence (joue en premier).
Des jeux où un joueur (« proie » ou « voleur ») n’a qu’un pion, et où l’autre joueur (« chasseurs » ou « chiens » ou « gendarmes ») doit essayer de bloquer l’unique pion de l’adversaire sur un graphe, existent depuis l’antiquité sous le nom de jeux de l’ours. Ce nom viendrait de ce que chez les vikings, la proie à bloquer par les chasseurs s’appellerait l’ours. Le jeu était connu des latins et plusieurs graphes sont connus aujourd’hui, sur lesquels on jouait en général à 3 chasseurs contre un seul ours. Les graphes reproduits aux pages 75 et 76 du livre comportent tous plus de 20 sommets (et parfois plus de 40). Et le degré minimal étant 3, il faut 3 pions pour les chasseurs.
Le graphe ci-dessus ne comportant que 6 sommets, dont deux sont de degré 2, il est envisageable de n’utiliser que deux chasseurs, et la petitesse du graphe, ainsi que la jeunesse du créateur du jeu, incitent à remplacer l’ours par un ourson.
Le graphe a été créé par une enfant de 7 ans (pour le simple plaisir de dessiner un graphe [1]) et le jeu a été créé sur ce graphe par son petit frère à l’âge de 4 ans.
La position initiale et la règle des 16 coups sont de moi par contre. J’ai d’ailleurs utilisé pour cela les résultats énoncés dans l’article (profondeur du graphe du jeu par exemple).
Malgré sa simplicité, le jeu bénéficie d’un certain succès, et en y jouant, on sent vite que les chiots ont un avantage certain sur l’ourson. L’idée de projet en NSI, est de formaliser cela, en cherchant une stratégie gagnante. Pour cela, la théorie des graphes, déjà présente de par le fait que le jeu se joue sur un graphe, va servir, comme pour chaque jeu combinatoire connu. Avec, ici, un graphe du jeu qui se montre de taille raisonnable.
Modélisation
Pour représenter les positions du jeu, on commence par numéroter les sommets du graphe, ainsi :
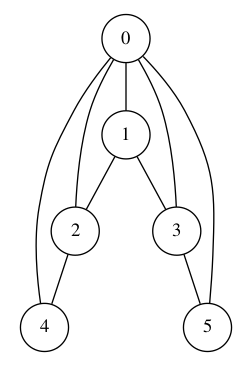
Une position sera représentée par une liste de sommets. On convient de mettre en premier le sommet où se trouve l’ourson, et ensuite, dans l’ordre croissant, les sommets où se trouvent les deux chiots. Enfin, la liste se termine par un 0 si c’est au joueur ourson de jouer, et par un 1 si c’est au joueur chiots de jouer.
Ainsi, la position initiale est représentée par la liste 0450 . Et la position bloquante vue ci-dessus est notée 5030 (5031 n’est pas bloquante puisque le 1 final signifie que l’un des chiots doit bouger et ainsi libérer provisoirement l’ourson).
Le graphe comprend 6 sommets, il y a donc 6 manières de placer l’ourson sur le graphe. Pour chacune de ces positions de l’ourson, il reste 5 sommets où placer deux chiots (indiscernables l’un de l’autre) et cela fait donc 5×4/2=10 manières de placer ces deux chiots sur les 5 sommets restants. Il y a donc en tout 60 positions possibles, et le graphe à construire comportera donc 60 sommets.
Et bien non : Il y a en fait 2 fois plus de positions. Pourquoi ?
Comme on l’a vu ci-dessus, la position codée 5030 est perdante (l’ourson en 5 est bloqué par les chiots en 0 et en 3) alors que la position 5031 ne l’est pas puisque l’un des chiots doit bouger (le 1 final signifiant que c’est aux chiots de jouer).
Il y a donc 60×2=120 sommets sur le graphe. On va les construire en Python. Pour cela on utilise deux variables, une liste de sommets et un dictionnaire associant à chaque sommet ceux vers lesquels on peut aller :
On fait prendre aux variables v (position du « voleur » ou ourson), g1 (gendarme numéro 1) et g2 (gendarme numéro 2) toutes les valeurs possibles allant de 0 à 5, et on ne garde que les cas où les trois variables prennent des valeurs différentes (un seul pion par sommet) et où les variables g1 et g2 sont classées dans l’ordre croissant :
for v in range(6):
for g1 in range(6):
for g2 in range(6):
if g1<g2 and g1!=v!=g2:
liste.append(str(v)+str(g1)+str(g2)+'0')
jeu[str(v)+str(g1)+str(g2)+'0']=[]
liste.append(str(v)+str(g1)+str(g2)+'1')
jeu[str(v)+str(g1)+str(g2)+'1']=[]
Télécharger
Après cela on peut afficher len(liste) et len(jeu) pour vérifier qu’il y a bien 120 sommets dans ce graphe.
On relie deux sommets s’il y a une règle du jeu qui permet d’aller du premier vers le second. Pour calculer l’existence de ce mouvement, on peut prendre une fonction Python, utilisant le graphe G du plateau de jeu :
G = [[1,2,3,4,5],[0,2,3],[0,1,4],[0,1,5],[0,2],[0,3]]
L’existence d’un mouvement est définie par cette fonction :
def mouvement(a,b):
if a[-1]==b[-1]:
return False
if a[-1]=='0':
if a[1]==b[1] and a[2]==b[2]:
return int(b[0]) in G[int(a[0])]
return False
else:
if a[0]==b[0]:
if a[1]==b[1]:
return int(b[2]) in G[int(a[2])]
if a[2]==b[2]:
return int(b[1]) in G[int(a[1])]
if a[1]==b[2]:
return int(b[1]) in G[int(a[2])]
if a[2]==b[1]:
return int(b[2]) in G[int(a[1])]
Télécharger
Le premier test porte sur l’identité du joueur, et rappelle qu’un même joueur ne doit pas jouer deux fois de suite. Le second test sépare le cas où
- c’est à l’ourson de jouer (a[-1]==’0’) : dans ce cas aucun chiot ne doit avoir bougé, et il doit y avoir une arête du graphe G allant de l’ancienne position de l’ourson, à la nouvelle ;
- c’est aux chiots de jouer : dans ce cas il ne faut pas que l’ourson ait bougé, et il faut qu’un seul chiot ait bougé. On est obligé de considérer 4 cas parce que si g2 (qui est à une position de numéro élevé) va vers un numéro inférieur à g1, la condition selon laquelle v1 est inférieur à v2 amène à intervertir leurs deux positions.
Pour finir de construire le graphe, on ajoute une arête entre deux sommets chaque fois qu’il existe un mouvement possible du jeu, allant de la première position vers la seconde :
for a in liste:
for b in liste:
if mouvement(a,b):
jeu[a].append(b)
Télécharger
C’est ici que la variable liste trouve son utilité : elle permet de parcourir tous les sommets.
Voici le graphe de toutes les positions du jeu :
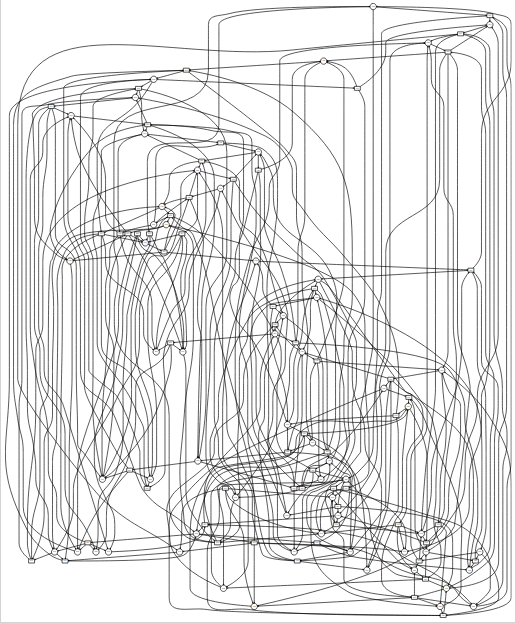
Pas facile de s’y retrouver ! Mais il y a une technique qui permet de trouver une éventuelle stratégie gagnante, en coloriant le graphe ci-dessus. La coloration est décrite dans cet article et se fait en partant de la fin (positions gagnantes) puis en remontant récursivement. Voici un exemple, appliqué à un jeu de type Nim (ces jeux sont décrits dans le chapitre 6 du livre) :
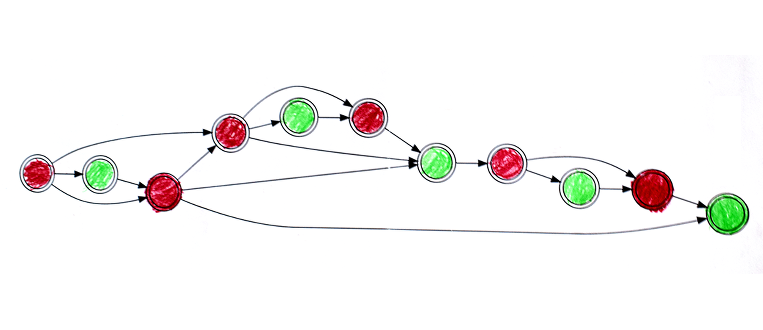
L’ennui avec le gros graphe ci-dessus, c’est qu’on a du mal à y voir s’il y a des cycles. Si c’est le cas, l’existence même d’une stratégie gagnante est compromise !
Ou pas...
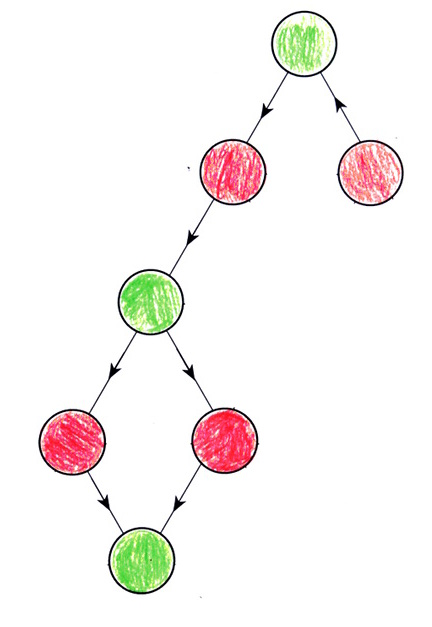
Voici un exemple de graphe orienté (type Nim) comportant des cycles :

Les cycles sont en bas à droite. Ce graphe a été colorié selon l’algorithme évoqué ci-dessus (rouge si ça peut aller vers du vert, vert si ça ne va que vers du rouge), par des collégiens, lors de la semaine des mathématiques 2019. Les collégiens ont vite vu que l’algorithme ne permet pas de colorier les sommets inclus dans des cycles, ils s’arrêtent donc là :
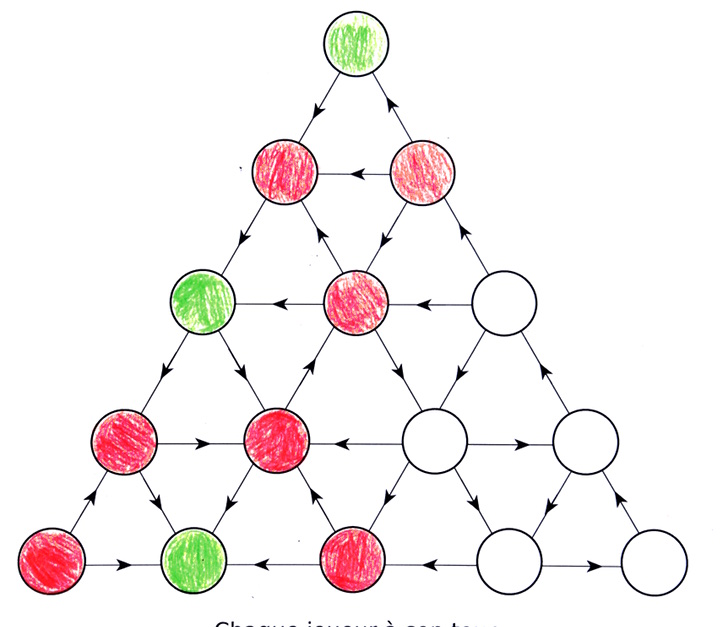
En supposant que le sommet rouge en haut à droite est le départ (on ne peut y arriver que depuis un cycle), on peut se demander s’il existe quand même une stratégie gagnante depuis ce sommet. La réponse est oui, car le sommet tout en haut, qui peut être atteint depuis le départ, est vert. On peut donc essayer d’enlever les cycles, puisqu’ils ne font évidemment pas partie de la stratégie gagnante :
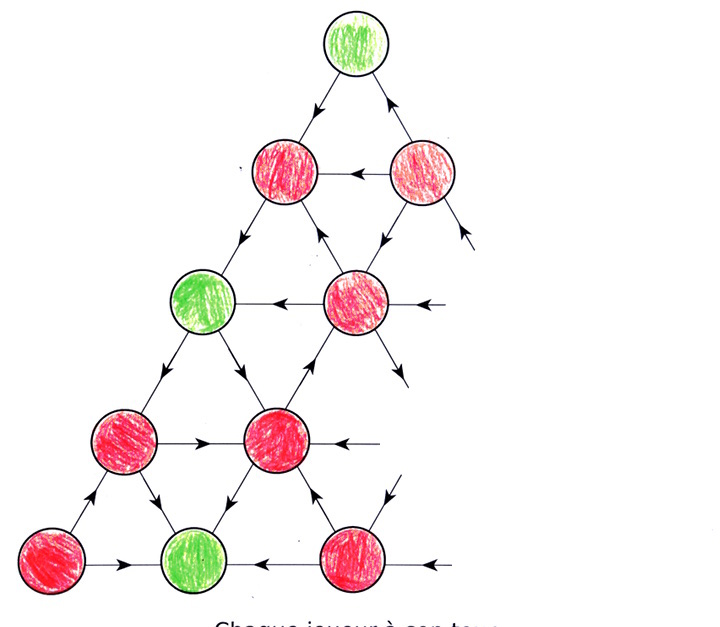
Le problème qui se pose éventuellement est celui des arcs allant vers un des sommets qu’on veut enlever :
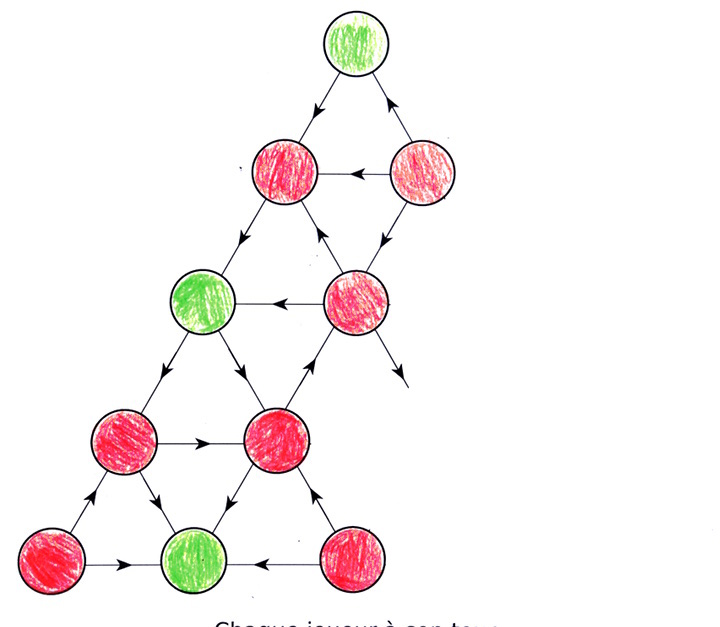
Mais comme cet arc ne fait pas partie de la stratégie gagnante (si on peut aller vers du vert, on n’a pas intérêt à faire un autre choix), on peut l’enlever sans problème. En fait on peut même enlever le sommet dont cet arc est issu, puisque le joueur qui pourrait aller vers ce sommet n’a pas intérêt à le faire :
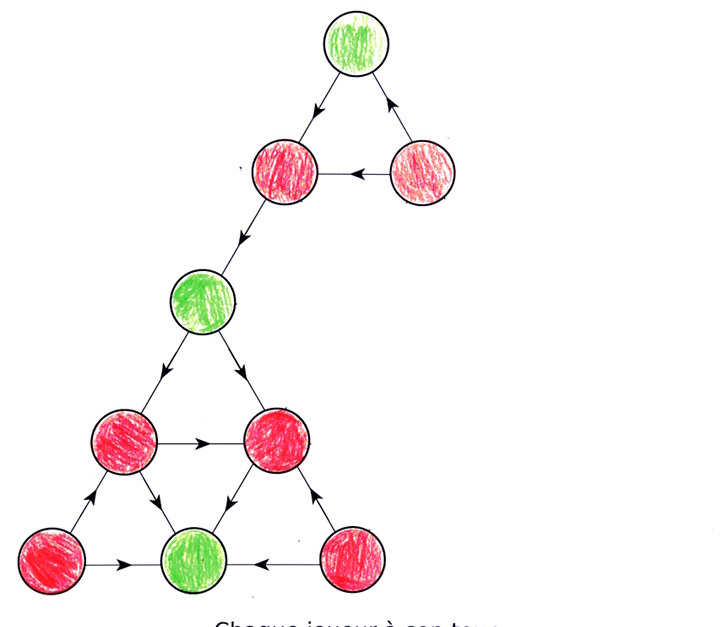
Il y a deux sommets, en bas, qui ne peuvent pas être atteints, et de ce fait ne font pas partie non plus de la stratégie gagnante. On peut donc les enlever sans problème :
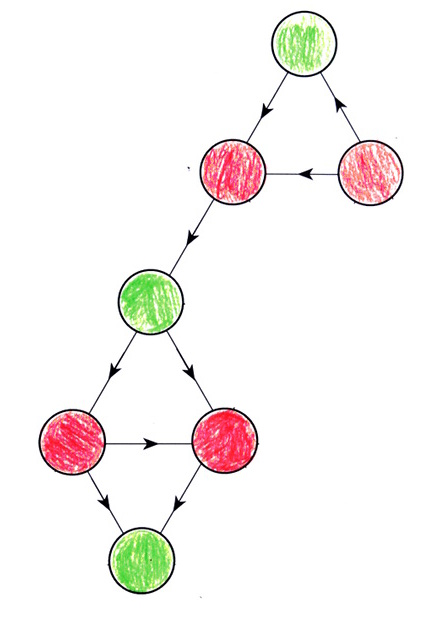
La simplification de graphes est le sujet du chapitre 9 du livre. On y voit d’autres applications de cette notion (ainsi que des jeux basés sur cette notion). Dans le cas présent, on n’a pas fini : il y a un arc vers le haut, que le joueur qui commence n’a pas intérêt à utiliser (puisqu’il mène à un sommet rouge, alors qu’il existe un sommet vert nettement préférable à celui-ci). On l’enlève donc aussi puisqu’il ne fait pas partie de la stratégie gagnante :
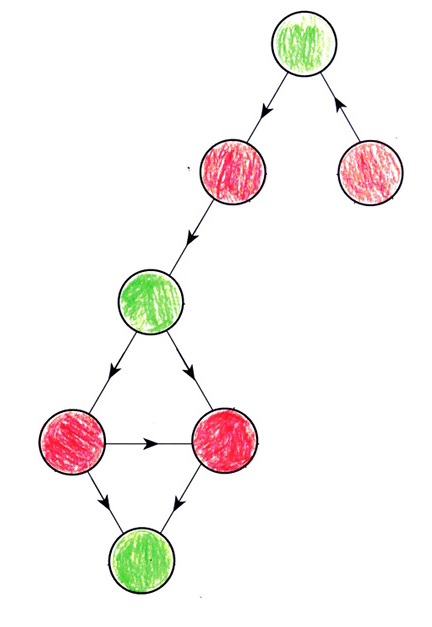
Une situation similaire apparaît en bas, on peut donc allègrement aussi enlever cette arête superflue :
Cela aboutit à deux choses qui sont intéressantes pour le jeu de l’ourson :
- l’existence de cycles n’interdit pas nécessairement celle d’une stratégie gagnante (il suffit de voir si on peut « les enlever »)
- s’il y a une stratégie gagnante, on peut la voir mieux en simplifiant le graphe.
Il y a plusieurs manières de donner à un sommet du graphe, une couleur. Par exemple on peut considérer le sommet comme un objet possédant un attribut couleur et calculer cet attribut pour les sommets l’un après l’autre. Ici on propose de créer trois listes :
- blancs est la liste des sommets non encore coloriés. Elle est donc initialisée à la liste de tous les sommets du graphe.
- rouges est la liste des sommets coloriés en rouge. Elle est donc initialisée à la liste vide, puisqu’au début on n’a encore rien colorié, a fortiori pas en rouge.
- verts est la liste des sommets coloriés en vert. Elle aussi est initialisée à la liste vide, ou plutôt à la liste des sommets gagnants (4020 et 5030) :
blancs = []
rouges = []
verts = []
for a in jeu:
if len(jeu[a])==0:
verts.append(a)
else:
blancs.append(a)
Télécharger
Pour colorier un sommet, on applique donc la règle suivante :
- si depuis le sommet a, il existe (any) un sommet b accessible et déjà colorié en vert, alors a est rouge,
- si tous les sommets accessibles depuis a sont rouges alors a est vert.
En Python l’algorithme s’écrit ainsi :
for a in blancs:
t = [b in verts for b in jeu[a]]
if any(t):
rouges.append(a)
blancs.remove(a)
u = [b in rouges for b in jeu[a]]
if len(u) and all(u):
verts.append(a)
blancs.remove(a)
Télécharger
Par contre le coloriage ci-dessus doit être effectué répétitivement, jusqu’à ce que plus aucun sommet ne soit encore coloriable. Une fois que c’est fait, la liste des sommets encore blancs révèle l’existence de cycles et de parties nulles. Pour le jeu de l’ourson, tous les sommets sont coloriés à la fin (60 sommets en rouge et 60, en vert). Il existe donc une stratégie gagnante au jeu de l’ourson.
L’algorithme de coloriage, appliqué au gros graphe ci-dessus, donne ce nouveau graphe :

Pas facile de s’y retrouver, en effet il y a des arêtes superflues : si un sommet est rouge, cela signifie qu’un de ses successeurs est vert, les autres successeurs sont donc inutiles puisque jouer au mieux, signifie ne pas y aller.
Cependant on constate que le sommet 0450 a été colorié en vert, ce qui signifie qu’il y a une stratégie gagnante pour les chiots. Le moins qu’on puise dire est qu’elle n’est pas très visible sur le graphe ci-dessus !
Une simplification possible du graphe passe par ce filtre : depuis un sommet rouge, n’aller que vers des sommets verts. Pour cela on crée un nouveau graphe appelé str1 (comme stratégie numéro 1) et on y copie le graphe configs mais en omettant les arêtes allant d’un sommet rouge à un autre sommet rouge :
str1 = {}
for a in configs:
if a in rouges:
str1[a] = [b for b in configs[a] if b in verts]
else:
str1[a]=list(set(configs[a]))
Télécharger
On obtient alors ce graphe :

Pas encore une vraie stratégie gagnante : il y a des cycles comme ici
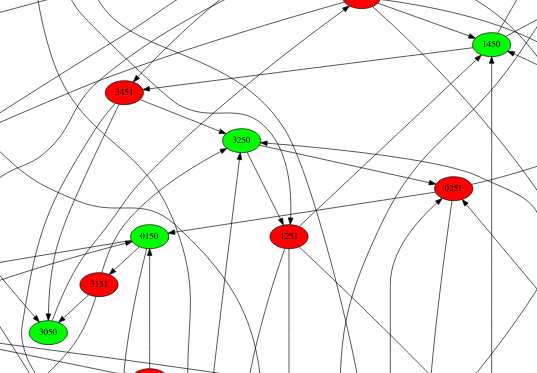
Pas facile de le voir hein ? Voici le même extrait du graphe, avec le cycle en exergue :
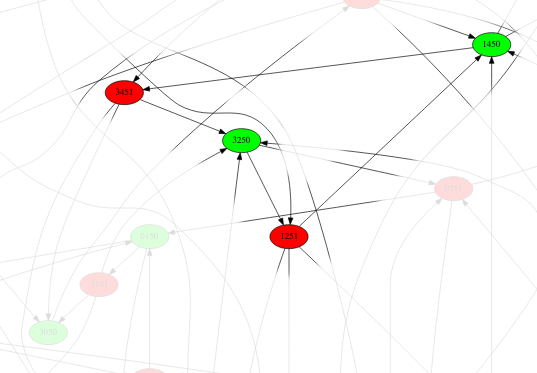
La position 1450 est marquée gagnante pour les chiots (coloriée en vert) car quel que soit le mouvement effectué par l’ourson depuis cette position, il perd (sommet colorié en rouge). C’est le cas notamment si l’ourson décide d’aller en 3 pour aboutir à la position 3451 qui est coloriée en rouge : les chiots peuvent depuis cette position, aller vers une position gagnante pour eux, par exemple la 3250. Mais dans ce cas l’ourson peut aller en 1251 qui permet aux chiots de revenir en 1450. Et ça boucle à nouveau. Voici le film de ce cycle sur le plateau de jeu :
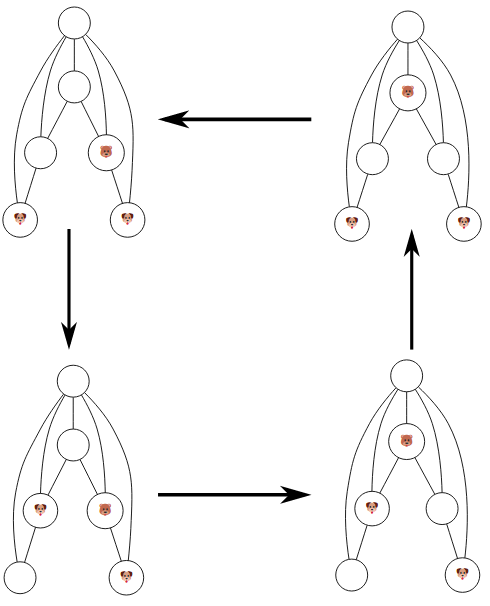
Depuis la position 3451, les chiots ne doivent donc pas aller en 3250 (3050 est mieux, ils ont gagné !). Ou alors, depuis la 1251, ils doivent éviter d’aller à nouveau en 1450. Dans les deux cas (enlever les arcs qui ferment un cycle d’ordre 4 ou ceux qui les ouvrent) il subsiste des cycles comme 4120 →0121→0230→4231→4120.
Et si on enlève tous les cycles d’ordre 4 le graphe obtenu n’est plus connexe et ne donne pas non plus une stratégie gagnante.
La présence de cycles dans le graphe des graphes, implique qu’il n’est pas possible d’y définir un ordre topologique [2], lequel aurait été bien pratique pour trouver une stratégie gagnante : il aurait suffi d’aller à chaque coup, le plus loin possible dans le graphe, c’est-à-dire se rapprocher le plus vite possible de l’arrivée. La même situation était apparue à propos de ce jeu, décrit dans le livre comme un jeu de blocage (qu’il n’est pas vraiment) [3].
Comment optimiser le choix à faire par les chiots, à chaque étape ? Autrement dit, comment faire pour sortir d’un cycle chaque fois qu’on le peut ? On va essayer ici une approche métrique, avec la notion de rang d’un sommet, le rang étant la longueur minimale d’un trajet allant du sommet, à une arrivée. On définit la fonction rang de façon récursive :
- le rang d’une arrivée est 0
- si un des descendants d’un sommet est de rang k et aucun descendant n’est de rang plus petit que k, alors ce sommet est de rang k+1.
Cette fonction récursive est modélisée par un dictionnaire Python :
rang = {}
for a in configs:
if len(configs[a])==0:
rang[a] = 0
for rg in range(1,8):
for a in configs:
if a not in rang and any([b in rang and rang[b]==rg-1 for b in configs[a]]):
rang[a]=rg
Télécharger
En évaluant
len(rang)
on trouve alors 120, ce qui veut dire que tous les sommets possèdent un rang. En évaluant
set(rang.values())
on a l’ensemble d’arrivée de la fonction rang :
{0, 1, 2, 3, 4, 5, 6}
Le rang maximal est donc 6, et c’est notamment le rang de 0450, ce qui montre que la position initiale a été bien choisie, du point de vue de la complexité.
Une stratégie pourrait donc consister, pour les chiots, à aller systématiquement vers un sommet vert de rang inférieur :
str1 = {}
for a in configs:
if a in rouges:
str1[a] = [b for b in configs[a] if rang[b]<rang[a]]
else:
str1[a]=configs[a]
Télécharger
Cela produit ce graphe :
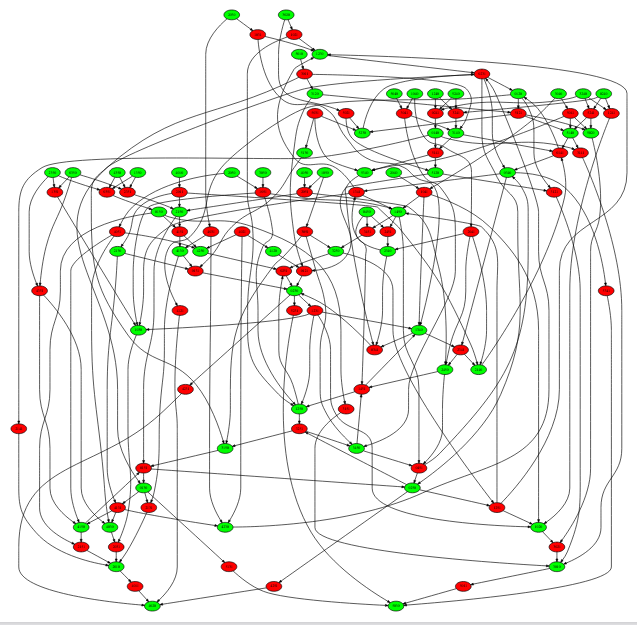
Et, en ne gardant que les sommets atteignables depuis le départ 0450, on n’a plus que 58 sommets sur le graphe :
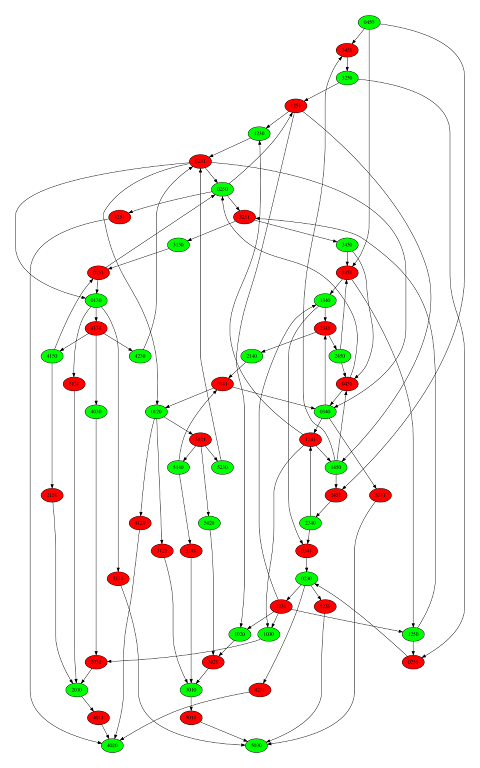
Mais hélas, il reste des cycles, comme celui-ci :
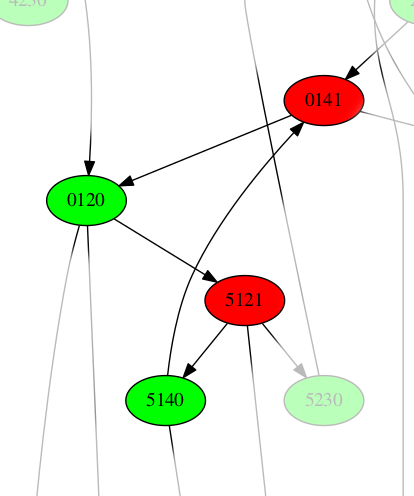
En affichant les rangs à côté des positions, on comprend mieux l’origine du problème :
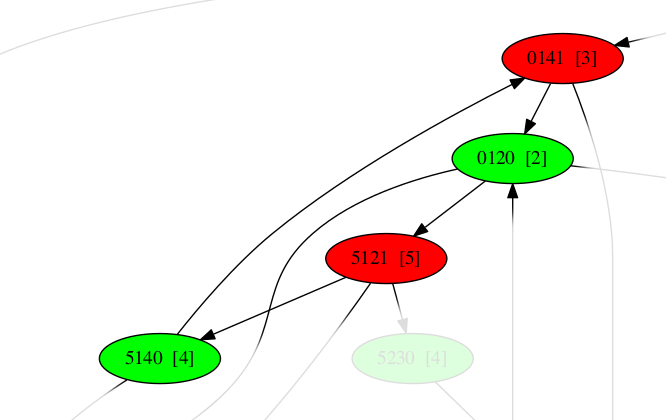
En allant du rang 3 au rang 2, puis du rang 5 au rang 4, les chiots jouent dans leur intérêt qui est de faire baisser le rang. Mais l’ourson, lui, n’a pas le même but : au contraire il cherche à faire augmenter le rang. Ce qu’il fait en allant du rang 2 au rang 5 (de la position 0120 à la position 5121).
Depuis la 0141 qui est de rang 3, les chiots, en ayant choisi la 0120 qui est de rang 2, ont bien joué, mais n’ont pas joué au mieux. Ils auraient pu jouer aussi la 0340 qui est aussi de rang 2, mais qui est aussi dans un cycle.
Depuis la position 5121, en jouant 5140, les chiots ont là encore bien joué (en passant du rang 5 au rang 4) mais cela permet à l’ourson de rester dans le cycle. À la place ils peuvent jouer
- 5230 qui est aussi de rang 4 mais qui permet à l’ourson de cycler sur 0231 (puis retour en 0120)
- ou 5020 qui est aussi de rang 4, mais permet de gagner à coup sûr (5020→3021→3010→5011→5030 ourson bloqué)
Le rang n’est donc pas une bonne métrique pour calculer ne serait-ce qu’une heuristique gagnante. Y en a-t-il une autre (métrique) ?
L’idée exposée dans cet article et celui-là revient, dans le cas présent, à pondérer le graphe des 120 sommets, puis à modifier la pondération au cours du jeu.
Le graphe (construit à partir de la liste des sommets) devient alors
for a in liste:
configs[a] = {}
for a in liste:
for b in liste:
if mouvement(a,b):
configs[a][b] = 1
Télécharger
À chaque sommet a n’est plus associé une liste (d’adjacence) des sommets b adjacents à a, mais un dictionnaire qui, à chaque sommet b, associe un poids initialisé à 1.
Pour choisir un sommet au hasard selon son poids, on peut utiliser l’algorithme vu dans cet article (variables aléatoires en terminale). Par exemple, en ayant importé le module random :
def choix(stats):
r = random() * sum(stats.values())
s = 0
n = 0
for k in stats:
s += stats[k]
if s>=r:
return k
Télécharger
En simulant 1000 parties au hasard on peut voir quels sont les choix gagnants au dernier coup :
for exper in range(1000):
S = '0450'
while len(configs[S]):
h = S
S = choix(configs[S])
configs[h][S] += 1
Télécharger
On a quelque chose comme ceci pour la fin du graphe :
4121 {'4230': 1, '4020': 57, '4010': 1}
4251 {'4150': 1, '4230': 1, '4050': 1, '4020': 97}
5231 {'5020': 1, '5120': 1, '5030': 137, '5130': 1, '5340': 1}
5341 {'5230': 1, '5030': 127, '5040': 1, '5140': 1}
4011 {'4150': 1, '4130': 1, '4030': 1, '4120': 1, '4020': 190}
5131 {'5010': 1, '5030': 67, '5230': 1}
4231 {'4250': 1, '4130': 1, '4030': 1, '4120': 1, '4020': 136}
5011 {'5020': 1, '5120': 1, '5030': 197, '5130': 1, '5140': 1}
On voit par exemple qu’il est statistiquement intéressant, depuis la position 5011, de jouer 5030, plutôt que n’importe lequel des 4 autres choix.
À ce stade, rien ne vaut l’expérimentation personnelle : peut-on trouver à l’aide des statistiques sur le jeu, un graphe donnant toute la stratégie gagnante, y compris l’évitement des cycles ?
Le logiciel ludii est programmé en [Java (langage)] et possède lui-même un langage de description des jeux, qui ressemble beaucoup à du Lisp. Mais ce n’est pas tout : ce logiciel est assorti d’une base de données assez complète sur les jeux dits « abstraits ». Dans ludii, les plateaux (pour les jeux à plateau, ce que ne sont pas par exemple les dominos, les jeux de cartes etc) sont tous des graphes, et il y a des constructeurs de graphes classiques.
Pour le jeu de l’ourson, on constate que son graphe comprend 2 quadrilatères coupés chacun par une de ses diagonales :
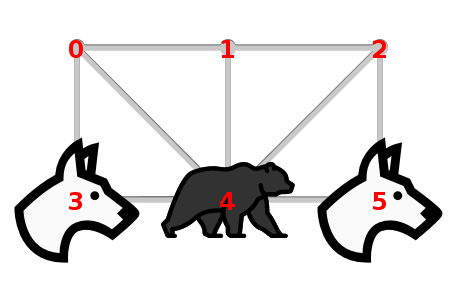
De plus, ludii permet d’afficher les coordonnées ou les indices (choix effectué ci-dessus) ce qui permet de savoir où placer les pièces du jeu au début :
(game "ourson"
(players 2)
(equipment
{
(board
(graph
vertices:{
{-1 1} {0 1} {1 1} {-1 0} {0 0} {1 0}
}
edges:{
{4 0} {4 1} {4 2} {4 3} {4 5} {3 0} {0 1} {1 2} {2 5}
}
)
use:Vertex
)
(piece "Bear" P2 (move Step (to if: (is Empty (to)))))
(piece "Dog" P1 (move Step (to if: (is Empty (to)))))
}
)
(rules
(start
{ (place "Bear2" (sites {"B1"})) (place "Dog1" (sites { "A1" "C1" })) }
)
(play (forEach Piece))
(end (if (no Moves Next) (result Mover Win)))
)
)
Télécharger
Mais du coup, ce graphe ressemble beaucoup à la moitié d’un plateau de marelle à 6 pions (plateau utilisé pour l’ancêtre du jeu de dames, appelé alquerque. On peut donc simplifier la création du graphe :
(game "ourson"
(players 2)
(equipment
{
("AlquerqueBoard" 2 3)
(piece "Bear" P2 (move Step (to if: (is Empty (to)))))
(piece "Dog" P1 (move Step (to if: (is Empty (to)))))
}
)
(rules
(start
{ (place "Bear2" (sites {"B2"})) (place "Dog1" (sites { "A2" "C2" })) }
)
(play (forEach Piece))
(end (if (no Moves Next) (result Mover Win)))
)
)
Télécharger
La seule différence avec la version précédente est que le sommet de degré 5 est en haut. On dispose donc les pièces sur la ligne du haut (ordonnée 2) au lieu de celle du bas (ordonnée 1).
Chacune des pièces du jeu (le Bear2 et les deux Dog1) ne peut bouger qu’en faisant un pas (Step) vers une destination (to) qui soit vide (is Empty). Et le jeu finit lorsque le prochain qui va jouer (Next) ne peut plus bouger (no Moves) auquel cas c’est le joueur qui vient de jouer (Mover) qui a gagné (Win).
Mais ce n’est pas tout : ludii permet aussi de construire un graphe où les sommets se touchent, ce sont alors des cellules adjacentes (ou non). Cette structure de graphe est classique dans bien des jeux (Senet, jeu de l’oie, dames, échecs etc) et on y trouve entre autres une structure en nid d’abeilles telle qu’utilisée dans le jeu de Hex. De fait, avec hex 2 on a un hexagone de côté deux cellules, soit 7 cellules en tout. En affichant les indices, on voit que la cellule 1 est en bas à droite, et on choisit de l’enlever avec (board ( remove (hex 2) cells:{1} )).
Le jeu est à peine plus compliqué qu’avant :
(game "ourson"
(players 2)
(equipment
{
(board ( remove (hex 2) cells:{1} ))
(piece "Bear" P2 (move Step (to if:(is Empty (to)))))
(piece "Dog" P1 (move Step (to if:(is Empty (to)))))
}
)
(rules
(start
{
(place "Bear2" (sites {"B2"}))
(place "Dog1" (sites {0 3}))
}
)
(play (forEach Piece))
(end (if (no Moves Next) (result Mover Win)))
)
)
Télécharger
Note : chacun des scripts précédents peut être téléchargé puis ouvert avec ludii.
Voici la position de départ du jeu :
La situation a maintenant une symétrie de rotation mieux visible, ce qui aidera à trouver une stratégie gagnante. En faisant jouer au mieux chacun des joueurs (avec comme IA, l’élagage alpha-bêta), on découvre que les chiens gagnent :
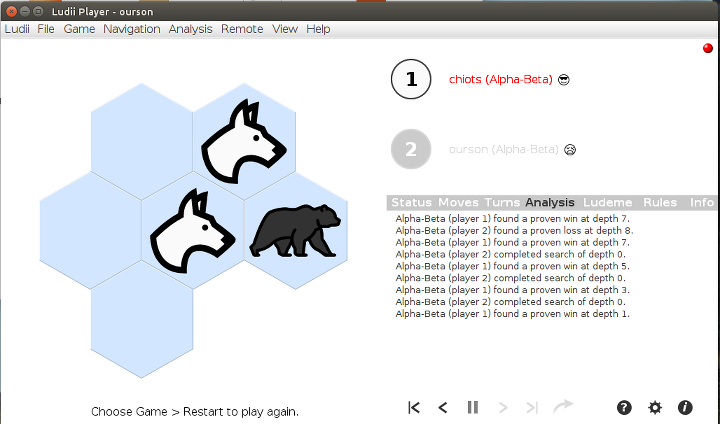
Voici le déroulé de la partie :

Ce qui permet d’exprimer la stratégie gagnante :
Bouger un chiot. Après cela l’ourson doit bouger donc quitter le centre. Mettre un des deux chiots sur le centre et ne plus le bouger : la partie libre du graphe est un couloir où l’autre chiot peut poursuivre l’ours jusqu’à le bloquer.
Pour savoir quel chiot mettre au centre, le principe est de s’arranger pour que dans le couloir, il y ait un nombre pair de cases entre l’autre chiot et l’ourson.
Cette stratégie gagnante a été trouvée en transformant le graphe (pour améliorer la visibilité du jeu) et en observant les IA jouer. Peut-être s’agit-il d’une bonne manière pour résoudre ce genre de problème : confier à l’IA les calculs difficiles, et la superviser avec un regard et une esthétique humains.
Conclusion
L’activité montrée ici a été annoncée en début d’article, comme propice à un projet en NSI. Après avoir lu (et expérimenté !) l’article, on peut en juger. L’avantage de ce genre de jeux inventés par de jeunes enfants est qu’outre leur relative simplicité qui permet une analyse exhaustive (ou pas, s’il y a des cycles !) ces jeux sont l’objet de problèmes ouverts. En voici quelques exemples pour lesquels on ne connaît pas à l’heure actuelle de stratégie gagnante :
- ce jeu créé à l’âge de 5 ans (et décrit tout à la fin du livre)
- ce jeu du même créateur mais plus récent (à l’âge de 8 ans)
- ce jeu qui ne se joue pas sur un graphe mais semble relativement simple à analyser, et surtout à modéliser [4].
Bons jeux [5] !
























