par Caroline Poisard, Dominique Tournès, Isabelle Cochet
Auteurs :
– Caroline Poisard, Laboratoire du CREAD (Centre de recherche sur les apprentissages et la didactique), ESPE (École supérieure du professorat et de l’éducation) de Bretagne, UBO (Université de Bretagne Occidentale), site de Quimper
– Isabelle Cochet, École de Pleurtuit, ESPE (École supérieure du professorat et de l’éducation) de Bretagne, UBO (Université de Bretagne Occidentale), site de Quimper
– Dominique Tournès, LIM (Laboratoire d’informatique et de mathématiques) et IREM (Institut de recherche sur l’enseignement des mathématiques), Université de la Réunion
Cet article peut être librement diffusé à l’identique dans la limite d’une utilisation non commerciale suivant la licence CC-by-nc-nd
N.D.L.R : "Nouveauté 2021
« Mallette boulier chinois pour la classe » - version 2, 2021
Les ressources de la « mallette boulier chinois » sont maintenant accessibles avec les liens suivants :
- Boulier virtuel (logiciel) en libre utilisation Sésamath – IREM de Brest :
https://www.univ-brest.fr/irem/menu/Ressources/Boulier-chinois-virtuel - Ressources de la « mallette boulier chinois en classe » : fiches pour les élèves, dossier pour le professeur, etc. :
- https://fabricamaths.hypotheses.org/mallette-boulier-chinois-version-2-2021 "
Introduction
Cet article présente une expérience, menée en classe de CE1 par un professeur que nous nommons Inès. Inès a intégré dans sa classe l’utilisation de l’abaque à jetons et du boulier chinois pour travailler la numération et en particulier les échanges. Cette expérience s’est nourrie de travaux en histoire et en didactique des mathématiques. En effet, Inès utilisait déjà le boulier chinois en classe et, à la suite de la présentation « L’abaque à jetons, outil d’apprentissage et de remédiation » (Tournès, 2014), elle a inclus dans sa progression l’étude de l’abaque à jetons pour introduire le boulier.
L’abaque [1] présente plus de souplesse quant aux nombres de boules (ou cailloux, boutons, etc.) que l’on peut manipuler sur une tige (rang ou colonnes de numération). C’est pour cela qu’Inès a choisi d’introduire en classe l’abaque puis le boulier (qui lui, est plus adéquat pour travailler sur des grands nombres). Nous commençons donc par un résumé des éclairages historiques et épistémologiques développés plus longuement dans l’article 1 de ce numéro. Ensuite, nous présentons la progression mise en place par Inès en CE1 (en 2014/2015) puis nous analysons l’ensemble des ressources matérielles et virtuelles utilisées pour travailler sur le nombre et la numération.
1) L’abaque à jetons : éclairages historiques et épistémologiques
Le Malade imaginaire, la pièce de Molière créée en 1673, commence par ces mots : « ARGAN, seul dans sa chambre, assis, une table devant lui, compte des parties d’apothicaire avec des jetons ; il fait, parlant à lui-même, les dialogues suivants : Trois et deux font cinq, et cinq font dix, et dix font vingt ; trois et deux font cinq. » Cette scène est instructive à plusieurs égards. Tout d’abord, elle nous rappelle qu’en Europe, jusqu’au 17e siècle et même après, on comptait en manipulant des jetons sur une table marquée de colonnes ou de lignes. Du côté de l’Asie, l’instrument de calcul usuel était plutôt le boulier, formé de boules coulissant sur des tiges. En français, le terme générique d’ « abaque » (mot venant du grec abax et du latin abacus) désigne tous ces instruments dans lesquels on place des petits objets identiques (cailloux, jetons, boules...) sur des colonnes, des lignes ou des tiges parallèles matérialisées sur un support plan, de manière à représenter des nombres et à calculer sur eux.
L’autre enseignement à tirer des comptes d’Argan est que la plupart des techniques de calcul, qu’elles soient mentales ou instrumentées, utilisent fortement des appuis à cinq. En effet, tant l’expérience quotidienne que les acquis des neurosciences nous montrent que notre œil et notre cerveau ne parviennent pas à dénombrer globalement et instantanément des quantités d’objets au-delà de quatre. C’est pour cela que quasiment toutes les numérations anciennes et modernes, et les instruments de calcul qui en découlent, utilisent des signes particuliers ou des dispositions géométriques spécifiques pour transcrire non seulement des regroupements par dix, mais aussi des sous-regroupements par cinq. Que l’on pense ici au « V » de la numération romaine, ou aux jetons et boules, appelés « quinaires », qui, par leur position particulière, représentent cinq unités sur les abaques.
L’un des plus anciens abaques connus, gravé sur une plaque de marbre, a été trouvé sur l’île grecque de Salamine. Il est daté du 5e ou 4e siècle avant notre ère. On connait aussi quelques petits bouliers portatifs romains que les archéologues situent vers la fin du 1er siècle de notre ère. De Salamine à Molière, tout ceci pour dire que la pratique des abaques à jetons et des bouliers a duré plus de 2000 ans avant que le calcul indien écrit, transmis à l’Europe par l’intermédiaire des Arabes, devienne usuel pour la majorité de la population [2]. Il pourrait donc sembler pertinent de faire revivre cette histoire en accéléré à nos élèves pour qu’ils surmontent à leur tour les différents obstacles épistémologiques rencontrés par l’humanité dans le passage difficile du calcul concret par manipulation d’objets sur les abaques au calcul abstrait par écriture de chiffres sur le papier. Par rapport au calcul indien, les abaques offrent notamment l’avantage d’être accessibles avant même l’apprentissage de l’écriture, et sont donc susceptibles de permettre à de jeunes enfants d’entrer plus tôt dans le monde numérique.
L’objet de cet article est justement l’analyse didactique d’une progression pour le CE1 qui, dans cet esprit, mêle les ressources anciennes fournies par les abaques à toutes les ressources modernes disponibles afin de faciliter la construction par l’élève de représentations visuelles et mentales efficaces dans le domaine de la numération.
2) De l’abaque « à boutons » au boulier chinois : une analyse d’intégration dans la classe d’Inès en CE1
Nous présentons maintenant une analyse de l’intégration en classe de CE1 de l’abaque « à boutons » puis du boulier chinois (pour d’autres exemples d’intégration en classe, voir : Poisard, Bueno-Ravel et Gueudet 2011, Riou-Azou 2014, Bueno-Ravel et Harel dans ce n° 51 de MathémaTICE). L’abaque peut s’utiliser avec des jetons, des cailloux, des haricots secs [3], des bouchons, etc. Inès, le professeur de cette classe possède une quantité de boutons nécessaire pour pouvoir utiliser l’abaque avec des boutons (à la place des jetons), nous parlons ainsi d’abaque « à boutons » [4] (figure 1). Le professeur utilise un TNI (tableau numérique interactif) ainsi que des ressources matérielles. Nous analysons comment les ressources matérielles et virtuelles s’articulent lors de cette progression (Poisard et al. 2015), ainsi que l’importance d’expliciter les différents codages du nombre et les synthèses après les phases de discussion.
2.1 La progression mise en place par Inès en classe de CE1
Inès participe au groupe de recherche MARENE [5], elle est également maître-formatrice. Cette séquence a été mise en place par en classe de CE1 en 2014/15. L’objectif de la séquence est de travailler en numération : « comprendre et réaliser des échanges entre les rangs, comprendre la notion de valeur et quantité » (extrait d’un entretien avec Inès). Inès a choisi de travailler en demi-groupe classe ou bien par ateliers lors de cette progression. Elle a également choisi de constituer des groupes d’élèves de niveaux homogènes. La table « à boutons » a été introduite en classe dès le mois de septembre et est utilisée lors du premier trimestre (environ 10 séances). Ensuite à partir du mois de janvier, le boulier chinois est proposé. Aussi bien pour l’abaque que pour le boulier, le professeur propose des manipulations matérielles (objets, fiches) et virtuelles (logiciel et TNI).
Pourquoi avoir choisi de débuter la séquence de numération par l’étude de l’abaque « à boutons » ? Les séances avec l’abaque « à boutons » sont ici pensées comme une introduction à celles avec le boulier chinois. L’abaque « à boutons » est inspiré de l’abaque romain et possède une partie réservée aux quinaires (partie haute) et une aux unaires (partie basse), mais le nombre de boutons à déposer n’est pas fixé. Sur le boulier chinois, chaque tige (ou rang) possède deux quinaires et cinq unaires, on peut donc inscrire au maximum 15 dans une tige donnée. Sur l’abaque, il est possible d’utiliser plus de jetons et par exemple de poser 3 (ou 4, ou 5, etc.) boutons dans les quinaires et 6 (ou 7, ou 8, etc.) dans les unaires. Ceci représente une certaine souplesse pour travailler en numération.
Pourquoi dans la progression proposer ensuite le boulier chinois ? Le boulier chinois a l’avantage, par rapport à l’abaque, de permettre d’inscrire et lire des grands nombres de manière aisée. En effet, les bouliers ont en général 13 ou 15 tiges qui correspondent au rangs de la numération, ce qui permet un travail intéressant sur les grands nombres à l’école.
2.2 Des ressources matérielles et virtuelles
Inès articule des ressources matérielles et virtuelles dans sa classe, aussi bien pour utiliser les abaques que les bouliers. Nous nous intéressons dans ce paragraphe, en particulier, aux ressources produites pour l’étude de l’abaque en classe.
Quel type des ressources sont utilisées dans la classe d’Inès ? Inès a fabriqué des cadres plastifiés qui sont utilisés avec des boutons. Elle possède un TNI et a créé des abaques virtuels : un tableau pour le cadre et des disques noirs pour former les jetons. La figure 2 présente l’exemple de l’inscription du 6 : deux manières sont présentées soit 6 unaires, soit 1 quinaire et 1 unaire (dans les unités). Inès a choisi d’utiliser la représentation de 5 unaires comme celle utilisée sur la face d’un dé. Cette représentation est en effet pertinente car notre œil ne peut pas dénombrer rapidement six éléments s’ils ne sont pas ordonnés (ceci explique le recours aux quinaires). Les manipulations pour les élèves sont donc matérielles (sur l’abaque « à boutons ») et virtuelles (avec le fichier sur le TNI).
Inès insiste sur l’importance d’une démarche d’investigation pour s’approprier les instruments : poser aux élèves la question de leur mode de fonctionnement permet une réelle réflexion sur la différence entre valeur et quantité, et sur la notion de rang de numération. Tout au long de sa progression, Inès met en place des phases de discussion où les élèves proposent et argumentent leurs réponses. Le TBI joue un rôle important afin de montrer à la classe les différentes propositions qui seront discutées. Un vidéoprojecteur, un affichage avec des aimants ou encore un visualiseur avec un boulier matériel peuvent également remplir ce rôle. Cette démarche permet également de travailler sur le langage, la verbalisation des élèves qui sont des compétences importantes à développer en mathématiques comme dans les autres disciplines.
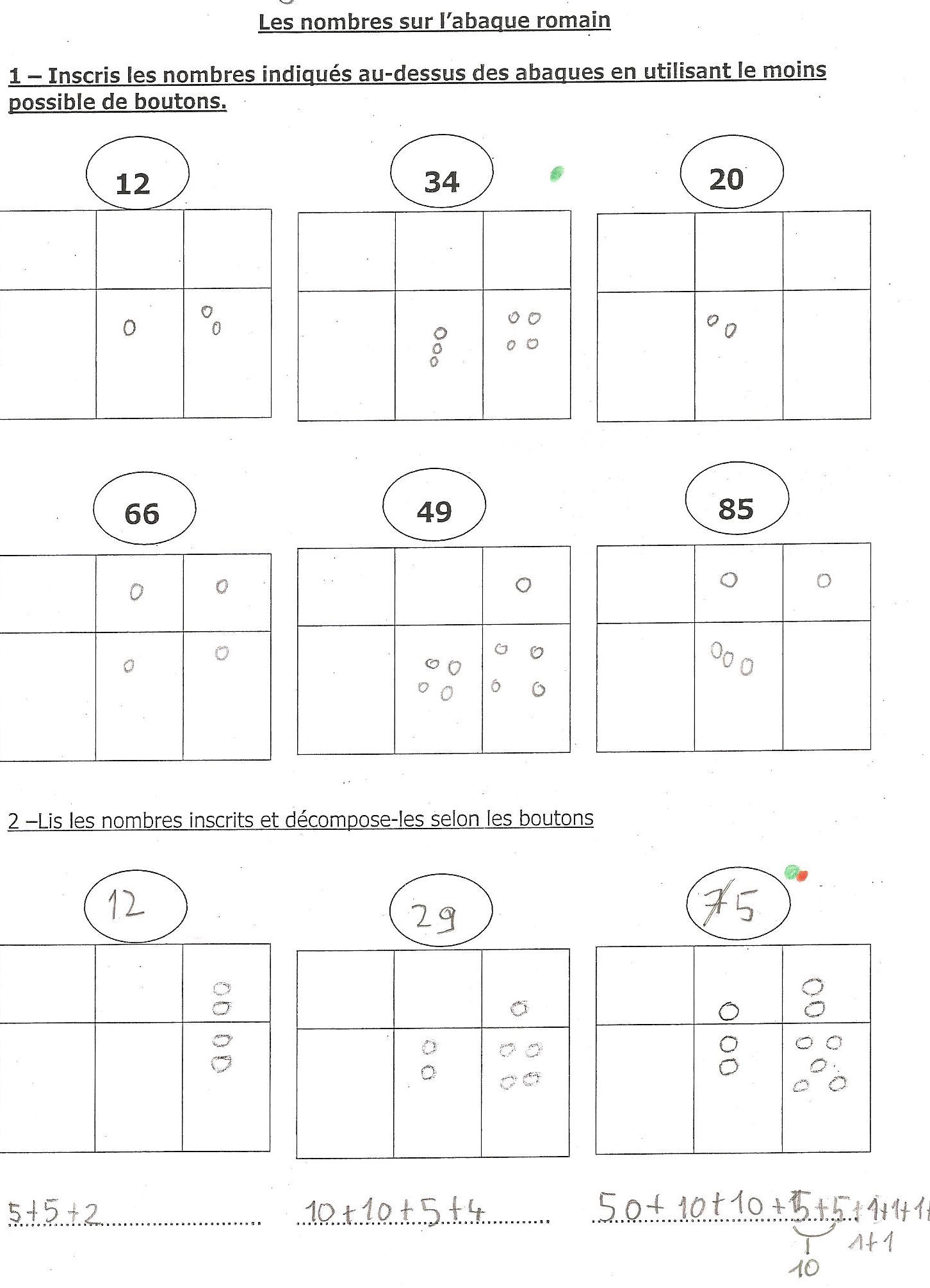
Les ressources matérielles sont également constituées de fiches pour les élèves. Il paraît important de produire des traces des apprentissages, ce qui est parfois délicat lors des manipulations. Sur cet exemple (figure 3), différents codages d’un même nombre sont demandés et un travail sur l’inscription « économique » des nombres (qui déplace le moins de boules possible) est proposé.
Inès soulève l’importance des synthèses écrites qui sont produites collectivement après une phase de discussions. Pour bien comprendre la différence entre valeur et quantité de jetons sur l’abaque, Inès propose une fiche synthèse sur la notion d’échange. La première fiche porte sur l’échange du cinq (5 unaires contre 1 quinaire) et la seconde sur l’échange du 10 (utilisation d’une ou de deux colonnes ou rangs). Les synthèses (ou traces écrites collectives) sont importantes : elles donnent à voir ce qui a été fait et appris en classe, elles constituent donc ce qu’on appelle en didactique « l’institutionnalisation » des savoirs (Brousseau, 2010).
À partir du mois de janvier, les élèves utilisent le boulier chinois qui permet de travailler sur un champ numérique plus large. Avec le boulier chinois, Inès articule également des ressources matérielles (bouliers, fiches élèves, synthèses, ardoises, mémo du 10) et des ressources virtuelles (logiciel avec ordinateurs et TBI) (figure 5). Les fiches élèves papier sont complétées par l’utilisation du logiciel boulier de Sésamath [6] qui permet d’afficher en chiffres l’inscription du boulier, ceci permet aux élèves de travailler en autonomie (pour un groupe).
Pour conclure, lors d’un entretien au mois de février, Inès juge que ses élèves de CE1 ont des connaissances renforcées en numération par rapport aux années antérieures, en particulier sur leur capacité à faire le lien entre « 1 centaine et 10 dizaines ». Ceci nous encourage donc à poursuivre notre analyse en terme d’apprentissage pour les élèves. Est-ce que cet apprentissage est dû essentiellement : à l’étude de l’abaque et du boulier en classe par les élèves ? À l’appropriation des ressources par le professeur, en particulier l’articulation de ressources virtuelles et matérielles ? Aux connaissances mathématiques et didactiques travaillées par cette appropriation par le professeur ? Voilà autant de questions qui sont des perspectives de recherche pour notre étude.
Conclusions
Cette expérience nous semble importante à plusieurs niveaux. Tout d’abord, elle montre que les séminaires de recherche que nous avons initiés sur le thème « le boulier chinois à l’école » (2013, 2014 et 2015, ESPE de Bretagne, CREAD – IREM et ESPE de la Réunion, LIM) sont des lieux de formation de formateurs qui permettent un travail de réflexion, de mise en place et d’analyse de séances en classe. Cette expérience montre également que les travaux en histoire et en didactique des mathématiques sont complémentaires et permettent des appropriations pertinentes en classe.
Sur les séances mises en place par Inès, nous retenons l’intérêt d’articuler des ressources matérielles et virtuelles, l’abaque et le boulier venant compléter les ressources déjà présentes dans la classe. Ces séances sont menées en questionnant les élèves sur les différentes procédures, les éventuelles erreurs (séances de type investigation) et sans oublier les phases de synthèse qui permettent de savoir ce qui a été appris en classe et donc de poursuivre les apprentissages. Enfin, l’autonomie des élèves est développée par la mise en place de fiches papier/crayon et d’autovalidation possible avec le logiciel.
Références
- Brousseau, G. (2010). Glossaire de quelques concepts de la théorie des situations didactiques des mathématiques. Site personnel de Guy Brousseau : http://guy-brousseau.com/biographie/glossaires/
- Poisard, C., Bueno-Ravel, L., & Gueudet, G. (2011). Comprendre l’intégration des ressources technologiques en mathématiques par des professeurs des écoles. Recherches en Didactique des Mathématiques, 31-2, 151-189. https://hal.archives-ouvertes.fr/hal-00603519
- Poisard, C., Gueudet, G., Bueno-Ravel, L. & Besnier, S. (2015, sept.). Le plaisir de manipuler en mathématiques à l’école : ressources matérielles et virtuelles. Les notes du CREAD, 1. http://cread.espe-bretagne.fr/sites/o-cedar.espe-bretagne.fr/files/u6/notes_1_bis.pdf
- Riou-Azou, G. (2014). La construction du nombre en grande section de maternelle avec un boulier chinois virtuel. Repères IREM, 98, 5-20. http://www.univ-irem.fr/spip.php?rubrique24&id_numero=98&id_article_reperes=651
- Tournès, D. (2014, avril). L’abaque à jetons, outil d’apprentissage et de remédiation. Journée d’étude « le boulier chinois à l’école ». ESPE de Bretagne, CREAD — IREM et ESPE de la Réunion, LIM.
- Tournès, D. (2016). Perspectives historiques sur les abaques et bouliers. MathémaTICE, 51.