Les TQuiz sont des jeux sérieux qui combinent des questionnaires classiques à la dynamique du jeu Tetris. Ils constituent une version dynamique des QCM (Questionnaires à choix multiples).

Figure 1

Exemple d’une page
de jeu (mode entraînement)

Lorsqu’on « joue », on est face à un écran (voir figure 1) où se déplace un élément, du haut vers le bas de l’écran, pendant une durée fixée par la personne qui crée le jeu. Cet élément mobile peut être une expression numérique, une formule, une figure, une image, un tableau… qui complète la question générale formulée en haut de l’écran. En bas de celui-ci figurent des cibles (trois ou plus) vers lesquelles le joueur doit diriger l’élément mobile pour obtenir une réponse correcte, avant que celui-ci ne tombe dans la cible qui correspond au choix par défaut (« je ne sais pas » dans la figure 1). Le joueur commande le déplacement de l’élément mobile à l’aide de la souris de l’ordinateur ou des touches « flèches » du clavier. Lorsque, dans le temps imparti, le joueur réussit à diriger l’élément dans la cible qui correspond à la réponse correcte, il marque des points. Par exemple, sur la figure 1, l’élément mobile est « –10x + 23x = – 33x ». Il est lié à la question, « Les égalités suivantes sont-elles toujours vraies ? ». Pendant le temps où l’élément mobile se déplace dans l’écran, il s’agit donc pour l’élève de répondre à la question suivante : « l’égalité –10x + 23x = – 33x est-elle toujours vraie ? ».
À droite de l’écran figurent deux jauges, la couleur verte correspond aux scores cumulés des réponses correctes et la rouge aux scores cumulés des réponses incorrectes ou « je ne sais pas ».
Le lien ci-dessous permet d’accéder directement au jeu présenté dans la figure ci-dessus.

https://www.epsilon-publi.net/EpsiT...

Il existe trois modes de fonctionnement du jeu :

• Mode découverte (fond d’écran vert) : il est possible d’arrêter la chute de l’élément pour augmenter le temps de réflexion sur la cible correcte. Il apparaît systématiquement une justification pour chacune des réponses.
• Mode entraînement (fond d’écran bleu) : il est toujours possible d’arrêter la chute de l’élément. Une justification apparaît seulement lorsque la réponse est fausse.
• Mode test (fond d’écran orange) : il n’est pas possible d’arrêter la chute de l’élément.

Ces modes permettent diverses exploitations en classe selon l’objectif visé. Par exemple, en phase d’apprentissage, le fait que la pause soit possible dans le jeu permet à l’élève de gérer son temps de réflexion. En mode test, avec l’absence de pause le côté ludique l’emporte : donner une réponse dans les temps devient un vrai challenge, développant ainsi l’agilité mentale.
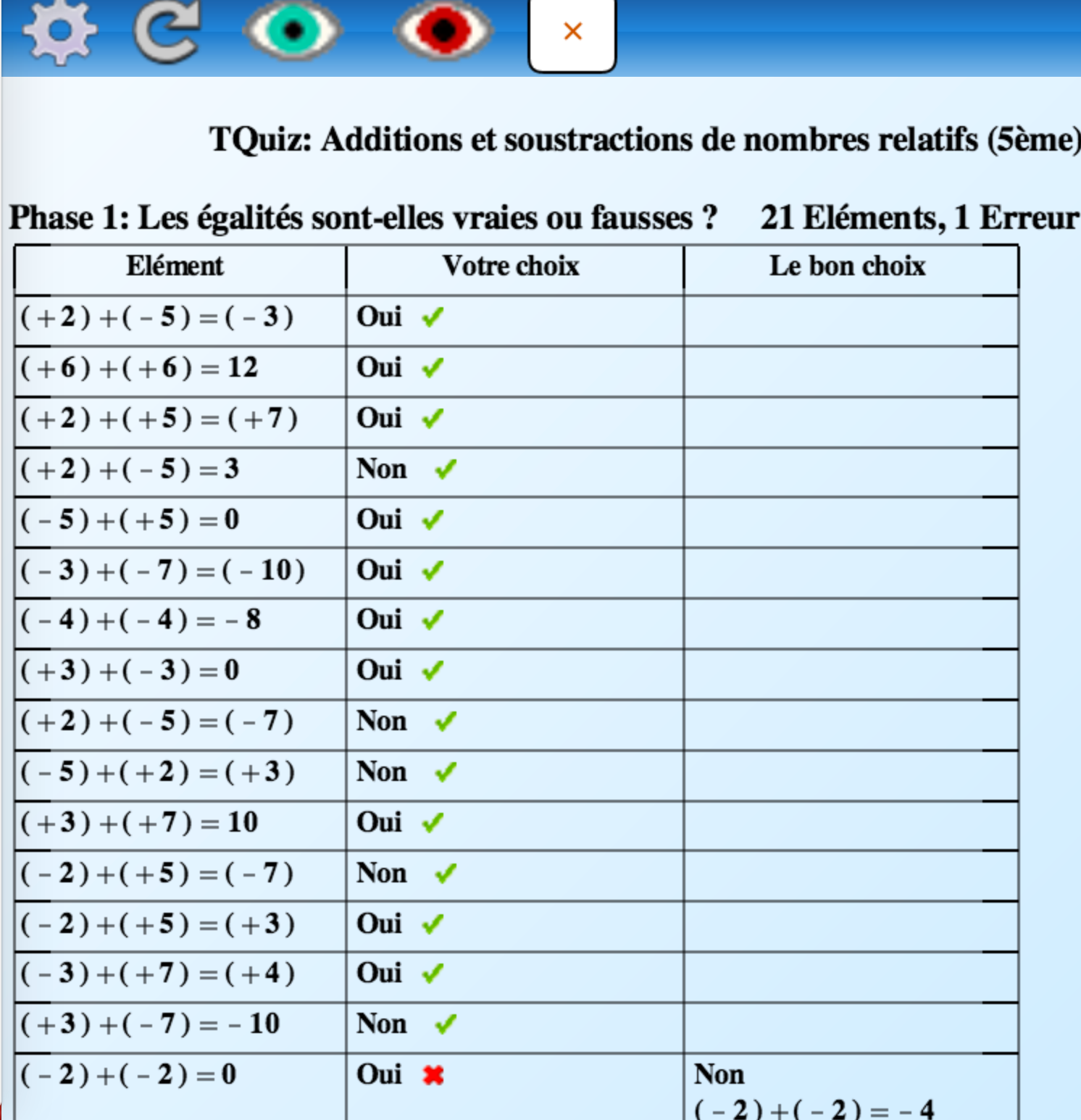
Il existe un rapport généré automatiquement à la fin du jeu lorsque l’on clique sur l’un des yeux . L’œil vert affiche toutes les réponses fournies, l’œil rouge seulement les réponses erronées et dans les deux cas, les rétroactions données pendant le jeu.
Ce rapport permet à l’élève d’avoir une vision globale ou partielle (uniquement les erreurs) de ses actions. Il peut revenir sur ses erreurs, voir ce qu’il a compris ou non, poser des questions à un enseignant-e ou un camarade pour comprendre.

Pour l’enseignant-e, c’est l’occasion d’individualiser son interaction avec l’élève. Par exemple, dans la situation suivante il peut observer que l’addition de nombres relatifs semble avoir été bien comprise contrairement à leur soustraction.

Retour au début de la partie
Retour au début de l’article

Du point de vue de l’enseignant-e

Facilité d’utilisation :

• le logiciel pour créer des TQuiz est disponible en ligne (https://tquiz.org/, onglet « Logiciels ») et il se nomme : epsilonWriter ,
• la prise en main est simple, comme nous l’expliquons un peu après,
• la diversité des modes d’utilisation permet de répondre à des objectifs variés et facilite la différenciation dans la classe.

Mutualisation et utilisation des ressources :

• des ressources sont disponibles dans la « Galerie » du site TQuiz (https://tquiz.org/), par exemple en mathématiques celles produites par les IREM de Grenoble et de Lyon ;

Figure 7

Extrait de la galerie du site TQuiz

• les ressources produites par d’autres enseignant-es peuvent être utilisées en l’état ou modifiées (pour celles qui sont enregistrées en « open source ») grâce à un lien direct vers le fichier source. Une explication détaillée est donnée sur le site TQuiz , à partir de l’onglet « Création » dans la section «  TQuiz open source » du paragraphe « Publication (mise à disposition sur le web) » ;

Figure 8

Une copie d’écran du site TQuiz

• le temps d’appropriation des ressources se limite à la prise de connaissance des contenus.

Du point de vue de l’élève

La prise en main est intuitive. L’autonomie des élèves est favorisée par la possibilité de choisir le mode de jeu qui leur convient et par l’existence de rétroactions.

L’aspect ludique et la nouveauté des TQuiz motivent les élèves :
L’environnement stimule tous les élèves, même les plus décrocheurs.
Les élèves ont envie d’améliorer leur score.
Les élèves disent : « apprendre en jouant », « mieux comprendre », « ça aide », « ça fait des révisions ».

Retour au début de la partie
Retour au début de l’article

Les TQuiz peuvent être utilisés de diverses façons :

• questions mentales de début d’heure,
• accompagnement personnalisé, remédiation, renforcement : différenciation et diversification faciles à mettre en œuvre,
• « musculation » en salle informatique, élèves seuls ou en binômes.

Des ressources concernant les TQuiz sont disponibles en ligne [*] :

• cliquer sur le lien suivant, https:/epsilon-publi.net,
• dans le menu en milieu de page, cliquer sur Toutes les ressources, 

Figure 9

Image extraite du site epsilon-publi

• enfin cliquer sur Ressources produites par les IREM de Lyon et Grenoble,

Figure 10

Image du site epsilon-publi « ressources »

ou directement sur le lien https://epsilon-publi.net/i/irem/.

Figure 11

Copie d’écran montrant des ressources produites par les IREM de Lyon et Grenoble

Retour au début de la partie
Retour au début de l’article

Claire, enseignante au collège

J’utilise particulièrement les TQuiz en mode entraînement, lors d’activités rapides en début d’heure. Les éléments tombent, avec des pauses possibles, et les élèves se mettent d’accord sur la réponse. Les débats engagés permettent de confronter diverses procédures et sont l’occasion de remédiations sur de nombreuses notions.
Les élèves sont très actifs lors de ces séances, ayant le sentiment, selon leurs propres mots, « d’apprendre en jouant ». Ce support permet une diversification des types d’activités proposés aux élèves et agit directement sur leur motivation.

J’utilise également les TQuiz en AP (aide personnalisée) comme outil de différenciation, les élèves pouvant jouer en autonomie grâce aux explications proposées dans le mode entraînement. Dans ce cas, ils s’attachent à améliorer leur score et n’hésitent pas à rejouer pour progresser. Ils souhaitent également accéder aux TQuiz depuis chez eux.

Émilie, enseignante au collège

Utilisation en AP :

J’utilise les TQuiz en AP en salle informatique, sur de nombreuses notions. Les élèves sont seuls ou en binômes et travaillent en autonomie.

J’impose souvent le thème de travail : par exemple, j’ai demandé à des élèves de 4ème de choisir un TQuiz permettant de retravailler la somme et la différence de relatifs en début d’année. Cela m’a permis de me rendre compte des difficultés générales de la classe sur cette notion et de commencer à y remédier.
Les élèves apprécient en général beaucoup de « jouer » avec leurs connaissances et de les renforcer, tout en travaillant à leur rythme. Ils cherchent à comprendre leurs erreurs afin d’augmenter leurs scores. Les élèves les plus à l’aise choisissent souvent le mode Test pour se stimuler et s’auto-évaluer.
L’accès au rapport généré automatiquement à la fin du jeu permet aux élèves d’avoir un bilan sur leur activité (autoévaluation). Il me permet également de contrôler le travail de chacun et d’effectuer une analyse différenciée des erreurs, formative pour l’élève.

Utilisation en question Flash :

J’utilise de temps en temps un TQuiz en question Flash : rituel de début de cours de quelques minutes, réalisé en classe entière. Le travail s’effectue à l’oral avec une pause possible pour stopper la chute de l’élément. L’intérêt est multiple : calcul mental, réactivation de connaissances, discussions mathématiques.

En conclusion

La prise en main des TQuiz est très simple. Aucune difficulté d’adaptation à l’outil n’a été rencontrée par les élèves. Ces derniers sont dans l’ensemble motivés par le questionnement proposé sous cette forme. L’utilisation des TQuiz a permis une meilleure compréhension de certaines notions chez de nombreux élèves qui font souvent référence à un TQuiz lorsque nous travaillons en classe des notions abordées auparavant dans ce jeu. Enfin, cet outil offre un support attractif à mon enseignement et permet de diversifier mes pratiques. J’apprécie également la variété des domaines mathématiques pouvant être abordés (numération, géométrie, algorithmique, etc.)

Concours IREM/TQuiz lors de la semaine des mathématiques 2017

Figure 12

Affiche de la semaine des mathématiques 2017

En 2017, dans le cadre de la Semaine des Mathématiques (13-17mars), l’Institut de Recherche sur l’Enseignement des Mathématiques de Grenoble a organisé avec la société Aristod un concours IREM/TQuiz pour les classes de CM2, 6e, 5e, 4e, 3e, 2nde de toute la France. 427 classes ont participé, correspondant à plus de 8 000 élèves.

Différents témoignages sont consultables sur le site
https://tquiz.org/semath2017/siteTemplate.php?lang=fr&page=accueil.php

Retour au début de la partie
Retour au début de l’article

De nombreux thèmes se prêtent à la création de TQuiz , qu’ils soient dans le domaine algébrique ou non avec des objectifs qui peuvent être multiples (renforcement d’une notion, meilleure assimilation en changeant de support, tests de connaissances…).
Dans les exemples suivants vous trouverez des TQuiz abordant la trigonométrie, l’algorithmique et les probabilités. Pour accéder aux TQuiz , cliquez sur les images [1].

NDLR : Les références des auteur-e-s des ressources sont disponibles quand on y accède sur l’application.

Figure 13

Page de jeu du TQuiz Trigonométrie , par Thomas Meyer.

Figure 14

Page de jeu d’un TQuiz algorithmique , par Émilie Quéma

Une fois le thème choisi, il faut décider du nombre de phases et de leur contenu.
Les phases permettent de mettre en place une progressivité dans les apprentissages ou de traiter de parties indépendantes.
Dans l’exemple ci-dessous, trois phases indépendantes ont été élaborées : recherche d’issues d’une expérience aléatoire, calculs de probabilités et calculs de probabilités à l’aide d’arbres.

Remarque : Les phases d’un TQuiz peuvent aussi porter sur des thèmes différents.

On crée un certain nombre de questions par phase. Il est possible de réutiliser des séries d’exercices que l’on utilise habituellement et de les présenter aux élèves sous forme de TQuiz.
On choisit également le type de cibles : « cibles changeantes » ou « cibles durables ».
Les cibles changeantes évoluent à chaque question alors que les cibles durables sont figées pour l’ensemble des questions d’une phase.

L’aspect technique est développé ci-dessous :

La création des TQuiz nécessite le téléchargement du logiciel gratuit développé par la société

Téléchargement [*] :

1. À partir du site Epsilon-publi, sélectionner « téléchargements » dans le menu « Auteurs »

   

   Figure 18

   Image du site Epsilon-publi

2. ou taper directement TQuiz dans un moteur de recherche et aller dans l’onglet « création »

   

   Figure 19

   Image du site TQuiz

   

   Figure 20

   Image du site TQuiz onglet « Création »

3. et télécharger le package 2.7 du 10 juillet 2017

Création d’un TQuiz :

1. Ouvrir EpsilonWriter creator 2.793 [2]
2. Cliquer sur « Fichier », « Nouveau »
3. Choisir « TQuiz (Cibles changeantes) » ou « TQuiz (Cibles durables) »

Figure 21

Image de Epsilonwriter creator lors de la création de TQuiz

Exemple « cibles changeantes » :

Figure 22

Extrait de la page de création du TQuiz Probabilités

Figure 23

Extrait de la page de création du TQuiz Probabilités

Remarque : pour indiquer les bonnes réponses, vous trouverez la coche verte dans l’onglet « génération ».

Figure 24

Image de epsilonwriter creator onglet « génération »

Exemple « cibles durables »

Figure 25

Extrait de la page de création du TQuiz Fonctions affines et linéaires

Enregistrement :

• Enregistrer le document sur son ordinateur : « Fichier » « Enregistrer »
• Créer un compte sur le site epsilon publi : aller dans l’onglet « Auteurs » puis cliquer sur « Inscription »

Figure 26

Image du site Epsilon-publi

• Pour visualiser et tester son TQuiz cliquer sur : « Enregistrer Web (TQuiz) »

Figure 27

Extrait de Epsilonwriter creator lors de publication d’un TQuiz onglet « web »

Retour au début de la partie
Retour au début de l’article

Ainsi, comme on peut le constater dans la galerie TQuiz (voir sur le site epsilon publi), diverses ressources TQuiz sont déjà disponibles. Certaines ont été créées par le groupe IREM. Elles sont triées par niveaux de classe. Elles peuvent être utilisées en l’état avec des élèves. Elles peuvent aussi être modifiées : il suffit de suivre les instructions données. Tous les lecteurs et lectrices de cet article sont invités à publier sur le site les ressources créées, même si elles s’inspirent de ressources existantes. Bonne création et bonne utilisation de TQuiz.

Retour au début de l’article