Les polygones isotoxaux interviennent dans de nombreux domaines. On les voit partout mais leur étude mathématique a longtemps été négligée. Cet article invite à y remédier.
Johannes Kepler est célèbre pour ses travaux en astronomie.
Dans son traité L’harmonie du monde (Harmonices Mundi) [1] écrit en 1619, il fait également une étude des pavages du plan et de l’espace dont on a redécouvert récemment l’intérêt [2].
On y trouve en particulier différentes planches de pavages du plan (ou d’une partie du plan) tout à fait saisissantes.

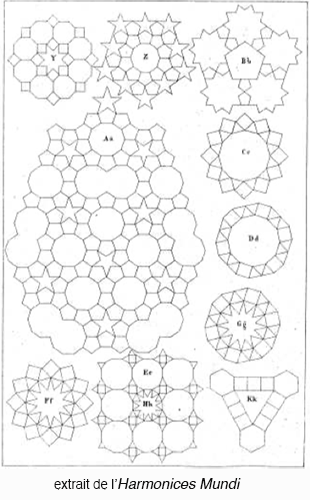
Les tuiles (pavés) de ces pavages sont (sauf exceptions) des polygones isotoxaux. On va ici définir précisément ce type de polygone et en faire une petite étude illustrée.
Cette étude généralise celle que l’on a entamée dans l’article La tête dans les étoiles à propos des polygones réguliers (convexes ou étoilés).


I) Généralités
Définition : un polygone est dit isotoxal si son groupe de symétrie (qui est un groupe généré par une rotation $r_{2\pi/nbCôtés}$ et une symétrie axiale) agit transitivement sur ses côtés : quels que soient deux côtés, il existe toujours une isométrie qui laisse globablement invariant le polygone et transforme un côté en l’autre.
Intuitivement, cela signifie qu’un polygone isotoxal a un seul type de côté.
En particulier, un polygone isotoxal est équilatéral. Mais la réciproque est fausse : il existe des polygones équilatéraux qui ne sont pas isotoxaux.
Exemple de polygone équilatéral non isotoxal :

L’octogone ci-dessus est construit « sur la base d’un carré » :

Cet octogone est équilatéral mais n’est pas isotoxal.
En général, un 2n-gone isotoxal a un groupe de symétrie diédral $D_n$. Il a n axes de symétrie qui relient un sommet et le sommet opposé. Par exemple, un losange non carré est un 2×2-gone isotoxal, avec un groupe de symétrie $D_2$. Ce polygone n’est pas isogonal.
Exemple :


L’octogone ci-dessus est isotoxal.
Son groupe de symétrie est $D_4$. Il est généré par une rotation d’un quart de tour et par une symétrie axiale.
Tous les polygones réguliers (convexes ou étoilés) sont isotoxaux. Un polygone régulier à n côté a pour groupe de symétrie $D_n$ (le double du n-polygone isotoxal général).
Par exemple, un carré a un groupe de symétrie diédral $D_4$.
Exemples de polygones isotoxaux
| Groupe de symétrie | |
| Nom | |
| Figure |
 |
| Groupe de symétrie | |||
| Nom | |||
| Figure |
 |
 |
 |
| Groupe de symétrie | |||
| Nom | |||
| Figure |
 |
 |
 |
| Groupe de symétrie | ||||
| Nom | ||||
| Figure |
 |
 |
 |
 |
Les polygones isotoxaux sont souvent utilisés dans des pavages qui utilisent des polygones réguliers convexes.
Les polygones isotoxaux sont les duaux des polygones isogonaux.
Pour définir un polygone isogonal, on procède généralement en deux temps :
- Tous les polygones réguliers, qu’ils soient convexes ou étoilés, sont isogonaux.
- Les autres polygones isogonaux sont les polygones équiangles à 2n côtés (n = 2, 3…) dont la longueur prend alternativement deux valeurs différentes, comme le rectangle. Ils ont un groupe de symétrie diédral $D_n$, avec n axes de symétrie reliant les milieux des côtés opposés.
Exemples de polygones isogonaux
| Groupe de symétrie | |
| Nom | |
| Figure |
 |
| Groupe de symétrie | |||
| Nom | |||
| Figure |
 |
 |
 |
| Groupe de symétrie | |||
| Nom | |||
| Figure |
 |
 |
 |
| Groupe de symétrie | |||||
| Nom | |||||
| Figure |
 |
 |
 |
 |
 |
Polygones isotoxaux
Polygones isogonaux
II) Le renouveau par la géométrie de la tortue
Pour chaque polygone régulier étoilé, il est naturel d’envisager le polygone concave qui lui est associé.

Ce nouveau polygone a 2.nbCôtés. C’est un polygone isotoxal.
On va s’intéresser à la façon de le tracer.

On voit clairement qu’il peut être construit « sur la base d’un pentagone régulier » :
On part d’un pentagone régulier convexe et on remplace chaque côté par une ligne brisée qui forme une pointe.
Dans l’article La tête dans les étoiles, on a vu qu’un polygone régulier à nbCôtés pouvait être construit par un script du type suivant :
fonction polygone(nbCôtés, côté, q)
répéter nbCôtés fois
Avancer(côté)
TournerDroite(360*q/nbCôtés)avec q entier premier avec nbCôtés.
Quand q = 1, on obtient un polygone régulier convexe.
Quand q ≥ 2, on obtient un polygone régulier étoilé, que l’on peut définir comme un polygone régulier non convexe ou bien comme un polygone régulier qui s’auto-intersecte.
Remarque : les polygones étoilés non réguliers ne sont pas formellement définis.
Pour le pentagone régulier convexe, le script est :
répéter 5 fois
Avancer(côté)
TournerDroite(72°)On remplace l’instruction
Avancer(côté)par :
TournerGauche(72°)
Avancer(côté)
TournerDroite(144°)
Avancer(côté)
TournerGauche(72°)On obtient un script suivant, qui trace le polygone isotoxal :
répéter 5 fois
TournerGauche(72°)
Avancer(côté)
TournerDroite(144°)
Avancer(côté)
TournerGauche(72°)
TournerDroite(72°)Soit
répéter 5 fois
TournerGauche(72°)
Avancer(côté)
TournerDroite(144°)
Avancer(côté)Quitte à modifier l’orientation initiale du polygone, on peut préférer cette formulation :
répéter 5 fois
Avancer(côté)
TournerDroite(144°)
Avancer(côté)
TournerGauche(72°)De façon plus générale, tout polygone isotoxal peut être tracé par un script du type suivant :
répéter n fois
Avancer(côté)
TournerDroite(180 - aPointe)
Avancer(côté)
TournerGauche(180 - aPointe – 360*q/n)

Ce script est caractéristique d’un polygone isotoxal, qu’il soit régulier ou pas.
Le cas du polygone régulier correspond au cas où aPointe = 180°.
Dans le cas où q = 1 et 0° ≤ aPointe ≤ 180° on obtient ce que l’on appelle communément une étoile (voir la figure ci-dessus qui évoque une étoile de mer).
Pour les étoiles qui découlent directement d’un polygone régulier étoilé de symbole de Schläfi $\{\dfrac{n}{q}\}$ [3], on a :
aPointe = 180 – 360*q/n
Ainsi, pour l’étoile à 5 branches : aPointe = 180 – 360/5*2 = 180 – 72*2 = 180 – 144 = 36°
C’est bien ce que l’on a trouvé plus haut.
De plus, on a : 180 - aPointe - 360*q/n = 360*q/n – 360/n = 360 (q – 1) / n
L’angle extérieur entre les côtés est $\beta$ = 360 (q – 1) / n.

Le polygone dual, qui est isogonal, a pour script :
répéter n fois
Avancer(côté1)
TournerDroite(180*q/n)
Avancer(côté2)
TournerDroite(180*q/n)Ce script est caractéristique d’un polygone isogonal, qu’il soit régulier ou pas.
Le cas du polygone régulier correspond au cas où côté2 = 0.
III) Généralisation : astres mathématiques
On propose ici une généralisation originale.
Comme on l’a vu plus haut, une étoile isotoxale peut être vue comme un polygone régulier convexe sur lequel à la place de chaque côté on a greffé une pointe. Mais on pourrait greffer n’importe quelle ligne brisée.
Définitions :
- On appelle parcours tortue la ligne brisée orientée correspondant à une séquence d’instructions Avancer(…) et Tourner(…).
- Pour tout parcours tortue, on appelle deltangle la somme algébrique des angles dans les instructions Tourner.
Définition :
On appelle astre à n rayons un polygone équilatéral qui peut être obtenu par un script tortue du type suivant :
répéter n fois
sous-scriptoù sous-script est un parcours tortue de deltangle égal à 360*q/n, avec q entier premier avec n.
Exemple : pour un sous-script de 6 instructions :
IV) Pavages
Comme on l’a évoqué dans l’entête de l’article, il existe de nombreux pavages intéressants à l’aide de polygones isotoxaux (et de polygones réguliers). Leur étude, initiée par Képler, a suscité un regain d’intérêt à la fin du siècle dernier.
On va se contenter ici d’en présenter dix exemples (sous forme de figures dynamiques DGPad).