NDLR : Cet article s’inscrit en continuité (mais aussi en rupture) dans le fil des articles déjà publiés au sujet de MathGraph32 dans MathémaTICE.
Le logiciel est devenu « Projet de Sésamath ». Son code a beaucoup évolué. De nouvelles fonctionnalités l’ont enrichi. Son auteur, Yves Biton, y travaille au quotidien, pour que les utilisateurs des manuels Sésamath disposent d’un outil performant pour tester les corrigés et traiter les exercices proposés.
Celles et ceux qui ne connaissent pas encore MathGraph32 pourront découvrir grâce à ces articles un logiciel performant, gratuit et vraiment libre.
Présentation
Les spécificités de MathGraph32
MathGraph32 a été édité pour la première fois en 2002 par le CNDP.
A l’époque, le logiciel n’était pas libre et ne fonctionnait que sous Windows. Il était écrit en C++ objet.
MathGraph32 fut le premier logiciel de géométrie dynamique à prendre en charge de façon native le calcul sur les nombres complexes.
En 2002 j’ai découvert en testant le logiciel un nouveau théorème que j’ai démontré, basé sur le théorème de Ptolémée. Une démonstration de ce théorème ainsi que des figures dynamiques sont visibles sur cet article.
En 2008 le logiciel est devenu gratuit (mais pas libre).
Je me suis en suite attaqué à une réécriture complète du logiciel en Java et la première version Java est sortie en 2009.
La version Java est trilingue : Français, Anglais et Espagnol. Un collègue Uruguayen s’est chargé de toutes les traductions en espagnol (sur le logiciel lui-même et sur le site de MathGraph32).
En mai 2010 j’ai passé la version Java sous licence libre GNU GPL3.
Depuis, le logiciel a constamment évolué.
C’est maintenant un projet de l’association Sesamath.
En 2017 je l’ai récrit en JavaScript et la version Java n’est plus supportée.
Je citerai les évolutions majeures du logiciels :
– Possibilité d’afficher des formules écrites avec du code LaTeX, cet affichage pouvant être dynamique grâce à des fonctions LaTeX spécifiques au logiciel.
– Enrichissement du moteur de calcul, avec par exemple la possibilité de calculer des dérivées partielles de fonctions de plusieurs variables (MathGraph32 sait calculer la dérivée d’une fonction réelle depuis sa première version), d’utiliser le calcul matriciel.
– Possibilité de mettre sur la figure des champs d’édition de formules permettant de modifier directement la formule d’une fonction sur la figure. La formule, entrée en ligne, peut-être visualisée en temps réel en écriture naturelle.
– Exportation de la figure, désormais en JavaScript.
– Exportation de la figure en LaTex-Tikz, qui fournit des résultats de grande qualité.
– Une ergonomie entièrement remaniée lors du passage à la version 5 avec des barres d’icônes déroulables et regroupées par type.
Les spécificités de MathGraph32
– MathGraph32 n’impose pas de nommer tous les objets créés. Il est possible de nommer un point ou une droite à la volée lors de sa création (un éditeur apparaît sous le point ou la droite créé) mais on peut choisir de ne pas lui attribuer un nom.
– MathGraph32 permet de créer des macros permettant d’agir sur la figure, dans un but pédagogique : Démasquer des objets cachés, lancer une animation sur la figure et bien d’autres choses encore.
– MathGraph32 permet de créer des lieux d’objets (générés par un point ou par une variable). On peut ainsi par exemple créer le lieu d’un courbe représentant une fonction dépendant d’un paramètre. Les graduations des repères sont elles mêmes des lieux d’objets
– MathGraph32 permet d’utiliser autant de repères qu’on le souhaite.
Il est possible bien sûr de créer une nouvelle figure munie d’un repère (avec l’icône  ).
).
Tous les types usuels de repère sont disponibles : Repère orthonormé, orthogonal, oblique, oblique normé et on peut choisir différents types de quadrillage. Les graduations des repères peuvent être déplacées avec la souris et leur taille peut être modifiée.
On peut aussi créer une figure avec un repère de type modifiable pour montrer aux élèves que certaines propriétés valables dans un repère orthonormal ne sont plus valables dans un repère quelconque (Utiliser l’icône  et choisir l’item Figure avec repère modifiable (avec ou sans vecteurs)).
et choisir l’item Figure avec repère modifiable (avec ou sans vecteurs)).
– Pour le collège (et la classe de seconde) MathGraph32 permet d’utiliser des outils spécifiques : un rapporteur virtuel, possibilité de créer un carré ou un triangle équilatéral en cliquant sur deux points, possibilité de créer un parallélogramme en cliquant sur trois points.
– Tous les styles de marques de segment et d’angle sont disponibles (et la taille des marque d’angle peut être modifiée par capture avec la souris). Pour le lycée, on peut aussi créer des marques d’angle orienté et même des marques orientées dans le sens direct et dans le sens indirect.
– MathGraph32 gère de façon native le calcul sur les nombres complexes et leur représentation graphique : On peut par exemple mesurer l’affixe d’un point dans un repère ou créer un point défini par son affixe.
– MathGraph32 prend complètement en charge le calcul sur les matrices réelles. Vous pouvez à ce sujet consulter cet article.
– Le protocole de la figure permet de voir comment la figure a été comprise. Une boîte de dialogue flottante apparaît et chaque objet est décrit de façon précise, avec un vocabulaire mathématique rigoureux. L’objet sélectionné dans la liste clignote sur la figure ainsi que ceux qui ont servi à sa construction.
La figure ci-dessous montre le début de la description d’une figure :

– MathGraph32 permet le reclassement d’objet, c’est-à-dire de déplacer un objet dans la liste des objets créés, vers le début ou la fin. Les boutons de droite sur la figure ci-dessus permettent ce type de reclassement.
Un exemple : Vous avez créé une fonction et sa courbe représentative. Finalement vous souhaitez que la formule de cette fonction dépende d’un calcul k (paramètre). Vous pouvez alors créer un calcul nommé k puis le reclasser avant la fonction f. Vous pourrez ensuite modifier la formule de la fonction f et la faire dépendre de k.
– MathGraph32 permet d’exporter une figure dans un page html, sans utilisation d’applet. Les points mobiles peuvent être capturés et les macros présentes sur la figure peuvent être exécutées. Pour cette exportation on peut utiliser des balises html spéciales. Voir cet article.
– MathGraph32 permet d’exporter la figure en code LaTeX tikz.
– MathGraph32 a des possibilités de traitement de calcul avancées qui permettent de mettre en ligne des exercices de calcul comme cet exercice de calcul de dérivée disponible sur LaboMep : L’exercice
– MathGraph32 permet de créer des figures en pseudo-3D. Ce n’est pas un vrai logiciel 3D mais il peut permettre de réaliser des figures parlantes pour les élèves comme par exemple la figure ci-dessous pour illustrer la notion de perspective centrale.
– MathGraph32 permet de créer ses propres macro-constructions et même d’implémenter des constructions de façon itérative ou récursive.
Exemples de Figures
Figures pour illustrer une notion de cours
Figures pour illustrer une notion de cours
– En seconde, la figure ci-dessous permet d’illustrer le signe d’une fonction affine.
Un éditeur de formule permet de modifier la formule de la fonction affine en haut et à gauche (une formule non affine est refusée).
Deux macros permettent de faire apparaître ou masquer le tableau de signes correspondant.
Vous pouvez capturer x avec la souris sur l’axe des abscisses et vous remarquerez que x figure aussi dans le tableau de signes avec le signe de f(x) mis en évidence dans le tableau.
– En Terminale S, la figure ci-dessous permet de visualiser l’intersection de deux plans donnés par une équation cartésienne.
Vous pouvez modifier les équations des deux plans, faire tourner la figure en capturant $\theta$ , zoomer ou dézoomer en cliquant sur les boutons + et - en bas et à droite de la figure.
Vous remarquerez que si les coefficients des équations de plans sont entiers et si les droites sont sécantes, les coordonnées définissant la droite d’intersection sont données sous forme d’entiers ou de fractions irréductibles.
– En première S, la figure ci-dessous permet de visualiser les cosinus et sinus d’angles remarquables.
Cliquez simplement sur une macro pour voir apparaître les cosinus et sinus de l’angle choisi avec visualisation graphique.
– En première, la figure ci-dessous permet d’illustrer la notion de loi binomiale et de chemins.
Capturez le curseur k pour choisir le nombre de succès.
Vous pouvez aussi changer la probabilité p de succès et faire varier N en bas et à droite de la figure en cliquant sur les boutons + ou - (N est le nombre de répétitions de l’épreuve élémentaire).
Vous pouvez capturer le curseur k pour faire varier le nombre de succès souhaités.
Vous remarquerez que les branches correspondant au nombre de succès souhaités se distinguent par leurs probabilités en rouge.
En bas et à droite de la figure, vous pouvez modifier la variable N en cliquant sur les bouton + ou - (de 2 à 5 générations de branches).
Cet article montre comment créer une figure analogue.
– En première S ou en seconde, la figure ci-dessous permet de faire comprendre le principe de la recherche de solutions d’équation f(x) = 0 par la méthode de dichotomie.
Cliquez sur les boutons + et - en bas et à droite de la figure pour changer d’étape (ces boutons sont associés à une variable).
Vous pouvez aussi modifier la formule de la fonction et l’intervalle [a ;b] de recherche de la solution (la fonction doit être strictement monotone sur [a ;b] et f(a) et f(b) de signes contraires).
– En première S (ou seconde) la figure ci-dessous disponible sur cette page permet d’illustrer la notion d’enroulement autour du cercle trigonométrique en mettant les angles remarquables en évidence.
Vous pouvez changer le pas d’enroulement en capturant le curseur du bas.
Cliquez sur les macro Animer pour lancer l’enroulement dans le sens direct ou indirect.
Cliquez sur la macro Initialiser pour réinitialiser la figure.
Retour en haut de la page
Figures de niveau avancé
Cet article montre comment utiliser les capacités avancées de calcul de MathGraph32 pour créer une courbe du « BlancManger » (il doit s’ouvrir dans un nouvel onglet du navigateur).
Cet article montre comment utiliser le calcul sur les nombres complexes pour représenter les attracteurs de Gumowski-Mira (il doit s’ouvrir dans un nouvel onglet du navigateur). Cet article s’est inspiré de cet article d’Yves Martin sur MathémaTICE.
Cet article montre comment représenter l’ensemble de Julia en utilisant des suites récurrentes complexes (il doit s’ouvrir dans un nouvel onglet du navigateur).
Les constructions
Les macro-constructions de Mathgraph32 permettent d’obtenir, à partir de certains objets d’une figure existante (les objets sources) la création de nouveaux objets.
Contrairement à la plupart des autres logiciels de même type, il est possible de voir comment a été créée une construction et éventuellement de repartir d’une construction existante pour la modifier en utilisant l’icône ![]() puis en choisissant l’item Fusionner les constructions de la figure.
puis en choisissant l’item Fusionner les constructions de la figure.
Les objets sources de type numérique doivent être déclarés en premier.
Pour les exemples ci-dessous il est conseillé d’utiliser la version 7.4.4 de MathGraph32 JavaScript que vous pouvez télécharger sur cette page ou une version ultérieure.
Premier exemple : Création d’une fonction polynôme de degré inférieur ou égal à 3 dont la courbe représentative passe par 4 points donnés.
Avant d’entrer dans cet exemple il faut remarquer qu’il est possible dans MathGraph32 d’obtenir directement la courbe d’une fonction polynôme de degré inférieur ou égal à n+1 passant par n points donnés via l’icône ![]() .
.
Il est maintenant possible dans la version JavaScript de MathGraph32 d’utiiser des calculs matriciels pour faire ce genre de choses mais nous ne les utiliserons pas ici pour montrer plus de fonctionnalités de MathGraph32.
Notre première macro-construction n’utilisera que des objets sources numériques.
Créez une nouvelle figure vierge, sans repère avec l’icône ![]() et en choisissant Figure sans repère et sans longueur unité.
et en choisissant Figure sans repère et sans longueur unité.
Nous avons d’abord besoin de créer 8 calculs correspondant aux coordonnées des quatre points par lesquels devra passer la courbe de la fonction polynôme.
Pour cela utilisez l’icône ![]() (qui se trouve dans l’avant-dernière rangée d’icônes) ou le raccourci clavier Ctrl - E.
(qui se trouve dans l’avant-dernière rangée d’icônes) ou le raccourci clavier Ctrl - E.
Créez ainsi 8 calculs nommés x1, y1, x2, y2, x3, y3, x4 et y4 avec comme valeurs respectives -2, 0, -1, 1, 0, 1, 1, 1 (les valeurs choisies n’ont pas vraiment d’importance, car ces calculs seront nos objets sources).
Pour créer notre fonction polynôme nous allons utiliser la formule de Legendre.
Avec l’icône ![]() créez une fonction nommée p comme sur la figure ci-dessous.
créez une fonction nommée p comme sur la figure ci-dessous.
Pour plus de facilité vous pouvez recopier le contenu du champ ci-dessous dans l’éditeur de formules de la boîte de dialogue .
y1*(x-x2)*(x-x3)*(x-x4)/(x1-x2)/(x1-x3)/(x1-x4)+y2*(x-x1)*(x-x3)*(x-x4)/(x2-x1)/(x2-x3)/(x2-x4)+y3*(x-x1)*(x-x2)*(x-x4)/(x3-x1)/(x3-x2)/(x3-x4)+y4*(x-x1)*(x-x2)*(x-x3)/(x4-x1)/(x4-x2)/(x4-x3)

Nous voulons que notre macro-construction fournisse comme objets finaux les coefficients de ce polynôme et la fonction polynôme correspondante.
Pour calculer les coefficients du polynôme nous allons utiliser la possibilité pour MathGraph32 de calculer des dérivées formelles. Nous pourrons ainsi calculer les coefficients de Taylor de ce polynôme. L’icône correspondante se trouve dans la troisième rangée d’icones à partir du bas (icônes de calcul et curseur).
Utilisez l’icône ![]() pour créer la fonction dérivée de p que nous appellerons p1 comme ci-dessous :
pour créer la fonction dérivée de p que nous appellerons p1 comme ci-dessous :
 .
.
Procédez de même pour créer la dérivée de p1 que vous appelerez p2. p2 sera donc la dérivée seconde de p (la touche de raccourci F2 permet de réactiver l’outil précédent).
De même créez la dérivée de p2 que vous appelerez p3 : (p3 sera donc la dérivée troisième de p).
Nous allons maintenant calculer nos quatre coefficients.
Les formules de Taylor donnent : $a=\frac{f’’’(0)}{3 !}$, $b=\frac{f"(0)}{2 !}$, $b=\frac{f’(0)}{1 !}=f’(0)$ et $d=f(0)$
Créez quatre nouveaux calculs a, b, c et d avec les formules suivantes :
– a : p3(0)/6
– b : p2(0)/2
– c : p1(0)
– d : p(0)
Nous pouvons maintenant créer notre macro-construction.
Pour gérer les macro-constructions dans la version JavaScript de MathGraph32, il faut activer des icônes supplémentaires en cliquant sur l’icône ![]()
Utilisez l’icône ![]() (création de construction) et choisissez l’item Choix des objets sources numériques.
(création de construction) et choisissez l’item Choix des objets sources numériques.
La boîte de dialogue ci-dessous apparaît :

Il faut transférer les éléments sources de la gauche vers la droite avec le bouton Insérer ou un doucle clic sur chaque élément.
Les éléments sources sont x1, x2, x3, x4, y1, y2, y3 et y4.
A la fin du transfert de la gauche vers la droite, la liste de gauche se retrouve vide comme ci-dessous.

Nous allons maintenant choisir les éléments finaux de notre construction.
Utilisez pour cela de nouveau l’icône ![]() et choisissez l’item Choix des objets finaux numériques.
et choisissez l’item Choix des objets finaux numériques.
Dans la liste proposée, sélectionnez p, a, b, c et d comme ci-dessous . Validez.

Il reste à achever notre construction. Utilisez de nouveau l’icône ![]() et choisissez l’item Finir la construction en cours.
et choisissez l’item Finir la construction en cours.
Remplissez la boîte de dialogue comme ci-dessous :

Vous pouvez copier le code ci-dessous dans le champ Informations sur la construction :
Fournit une fonction polynôme de degré inférieur ou égal à 3
dont la courbe passe par quatre points donnés
#1:Abscisse de point 1
#2:Ordonnées du point 1
#3:Abscisse de point 2
#4:Ordonnées du point 2
#5:Abscisse de point 3
#6:Ordonnées du point 3
#7:Abscisse de point 4
#8:Ordonnées du point 4Les lignes commençant par le caractère # serviront à donner une information à l’utilisateur lorsqu’il implémente la construction.
Vous allez maintenant enregistrer cette construction sur votre ordinateur sous le nom PolynomDeg3.mgc.
Pour cela activez l’icône ![]() (gestion des constructions) puis choisissez l’item Enregistrer une construction de la figure.
(gestion des constructions) puis choisissez l’item Enregistrer une construction de la figure.
Une boîte de dialogue apparaît. Dans la liste de gauche, notre seule macro construction est sélectionnée.
Cliquez sur le bouton Enregistrer puis enregistrez cette construction dans le dossier de votre choix. Il est préférable de choisir pour le nom du fichier le même nom que celui de la construction.
A noter que si vous enregistrez cette figure, la construction qu’elle contient sera contenue dans la figure enregistrée.
Deuxième exemple : Création de la courbe d’une fonction polynôme de degré inférieur ou égal à 3 passant par 4 points donnés.
Nous allons maintenant créer une autre figure et une autre construction utilisant la construction précédente.
Utilisez l’icône ![]() pour créer une nouvelle figure munie d’un repère (par exemple orthonormal mais ce n’est pas important).
pour créer une nouvelle figure munie d’un repère (par exemple orthonormal mais ce n’est pas important).
A l’aide de l’outil ![]() (point libre, première rangée d’icônes), créez quatre points libres que vous nommerez A, B, C et D.
(point libre, première rangée d’icônes), créez quatre points libres que vous nommerez A, B, C et D.
Déroulez la barre d’icône des mesures et cliquez sur l’icône ![]() (mesure d’abscisse dans un repère) pour mesurer l’abscisse des points A, B, C et D que vous nommerez respectivement xA, xB, xC et xD.
(mesure d’abscisse dans un repère) pour mesurer l’abscisse des points A, B, C et D que vous nommerez respectivement xA, xB, xC et xD.
Utilisez l’icône ![]() (mesure d’ordonnée dans un repère) pour mesurer l’ordonnée des points A, B, C et D que vous nommerez respectivement yA, yB, yC et yD.
(mesure d’ordonnée dans un repère) pour mesurer l’ordonnée des points A, B, C et D que vous nommerez respectivement yA, yB, yC et yD.
Utilisez l’icône ![]() (gestion des constructions) et utilisez l’item Incorporer une construction depuis un fichier. Allez chercher la construction PolynomeDeg3.mgc à l’endroit où vous l’aviez enregistrée, puis cliquez sur le bouton Ouvrir. Cette construction fait maintenant partie de votre figure.
(gestion des constructions) et utilisez l’item Incorporer une construction depuis un fichier. Allez chercher la construction PolynomeDeg3.mgc à l’endroit où vous l’aviez enregistrée, puis cliquez sur le bouton Ouvrir. Cette construction fait maintenant partie de votre figure.
Pour l’utiliser, utilisez à nouveau l’icône l’icône ![]() et choisissez l’item Implémenter une construction de la figure.
et choisissez l’item Implémenter une construction de la figure.
Une boîte de dialogue s’ouvre dans laquelle notre construction est sélectionnée. Cliquez sur le bouton Implémenter.
Une boîte de dialogue s’ouvre pour vous demander les objets sources.
Il faut par exemple affecter la mesure d’abscisse xA à l’élément source n°1 comme ci-dessous :

Affectez ainsi dans l’ordre xA, yA, xB, yB, xC, yC, xD, yD aux éléments sources 1, 2, 3, 4, 5, 6, 7 et 8, puis validez.
Si vous utilisez l’icône ![]() (pour voir et modifier les objets numériques) vous pourrez voir que notre figure comporte maintenant une fonction p et quatre calculs a, b, c et d qui sont les objets finaux de notre construction.
(pour voir et modifier les objets numériques) vous pourrez voir que notre figure comporte maintenant une fonction p et quatre calculs a, b, c et d qui sont les objets finaux de notre construction.
Nous allons maintenant créer la courbe représentative de la fonction p. Nous n’utiliserons pas pour cela l’icône ![]() car la courbe dépendrait de l’origine du repère. Nous allons donc implémenter une construction prédéfinie de MathGraph32.
car la courbe dépendrait de l’origine du repère. Nous allons donc implémenter une construction prédéfinie de MathGraph32.
Depuis que MathGraph32 a été récrit en JavaScript, les constructions prédéfinies ne sont plus incluses dans le logiciel mais fournies dans un dossier externe que vous devez télécharger sur le site de MathGraph32 sur cette page : https://www.mathgraph32.org/spip.php?article65
Une fois le fichier zip contenant les constructions téléchargé, décompressez le dans le dossier de votre choix.
Ouvrez le dossier Courbes et choisissez la construction Courbe Fonction Pour Construction Sur R. Cliquez sur le bouton Ouvrir. Cette autre construction fait maintenant partie de votre figure.
Pour l’implémenter, utilisez l’icône ![]() et choisissez l’item Implémenter une construction de la figure, sélectionnez la deuxième construction de la liste et cliquez sur le bouton Implémenter.
et choisissez l’item Implémenter une construction de la figure, sélectionnez la deuxième construction de la liste et cliquez sur le bouton Implémenter.
Affectez à l’élément source n°1 le repère (O,I,J) comme ci-dessous :

et de même affectez à l’élément source n°2 la fonction p puis validez.
La courbe apparaît. Vous pouvez si vous le souhaitez modifier sa couleur et son style de tracé avec l’outil ![]()
Nous allons maintenant créer une nouvelle macro construction qui, à partir d’un repère et de quatre points, construira la courbe de la fonction polynôme correspondante.
Utilisez l’icône ![]() (création d’une construction) et choisissez l’item Choix des objets sources numériques.
(création d’une construction) et choisissez l’item Choix des objets sources numériques.
Choisissez comme ci-dessous le repère (O,I,J) comme seul objet source numérique.

Utilisez maintenant l’icône ![]() , choisissez l’item Choix des objets sources graphiques et cliquez successivement sur les points A, B, C et D. Cliquez sur le bouton rouge
, choisissez l’item Choix des objets sources graphiques et cliquez successivement sur les points A, B, C et D. Cliquez sur le bouton rouge ![]() qui est apparu en bas et à droite de la fenêtre pour indiquer que le choix des objets sources graphiques est terminé.
qui est apparu en bas et à droite de la fenêtre pour indiquer que le choix des objets sources graphiques est terminé.
Nous allons maintenant choisir les objets finaux graphiques.
Utilisez de nouveau l’icône ![]() et choisissez l’item Choix des objets finaux graphiques.
et choisissez l’item Choix des objets finaux graphiques.
Cliquez sur la courbe (qui est notre seul objet final graphique) puis cliquez sur le bouton rouge l’icône ![]()
Choisissons maintenant les objets finaux numériques.
Utilisez de nouveau l’icône ![]() et choisissez l’item Choix des objets finaux numériques.
et choisissez l’item Choix des objets finaux numériques.
Remplissez la boîte de dialogue comme ci-dessous puis validez :

Il nous reste à finaliser notre construction. Cliquez sur l’icône ![]() , choisissez l’item Finir la construction en cours et remplissez la boîte de dialogue comme ci-dessous :
, choisissez l’item Finir la construction en cours et remplissez la boîte de dialogue comme ci-dessous :

Voici le code à coller dans le champ Infos :
Construit la courbe d'une fonction polynôme de degré inférieur ou égal à 4
passant par 4 points donnés. Dans les objets finaux, p est la fonction polynôme
et a, b, c et d sont les coefficients.
#1:Le repère
#2:Le premier point
#3:Le deuxième point
#4:Le troisième point
#5:Le quatrième pointUtilisez maintenant l’icône ![]() , choisissez l’item Enregistrer une construction de la figure et enregistrez cette nouvelle construction à l’endroit de votre choix en prenant de préférence le même nom pour le fichier que celui de la construction.
, choisissez l’item Enregistrer une construction de la figure et enregistrez cette nouvelle construction à l’endroit de votre choix en prenant de préférence le même nom pour le fichier que celui de la construction.
Nous allons pour finir créer une dernière figure dans laquelle nous utiliserons cette nouvelle construction.
Utilisez l’icône ![]() pour créer une nouvelle figure munie d’un repère par exemple orthogonal.
pour créer une nouvelle figure munie d’un repère par exemple orthogonal.
Utilisez l’outil ![]() pour créer quatre points libres à coordonnées entières dans ce repère. Il suffit de cliquer sur la figure pour créer chaque point. On peut ensuite les déplacer avec l’outil
pour créer quatre points libres à coordonnées entières dans ce repère. Il suffit de cliquer sur la figure pour créer chaque point. On peut ensuite les déplacer avec l’outil ![]() amis leurs coordonnées dans le repère restent entières.
amis leurs coordonnées dans le repère restent entières.
Il faut maintenant incorporer dans cette nouvelle figure la construction CourbePolyPar4Points.
Utilisez l’icône ![]() , choisissez l’item Incorporer une construction depuis un fichier, allez dans le dossier où vous avez sauvegardé la dernière construction et sélectionnez le fichier correspondant, puis cliquez sur le bouton Ouvrir.
, choisissez l’item Incorporer une construction depuis un fichier, allez dans le dossier où vous avez sauvegardé la dernière construction et sélectionnez le fichier correspondant, puis cliquez sur le bouton Ouvrir.
Pour implémenter cette construction, utilisez à nouveau l’icône ![]() et choisissez Implémenter une construction de la figure. Dans la boîte de dialogue qui s’ouvre, cliquez sur le bouton Implémenter.
et choisissez Implémenter une construction de la figure. Dans la boîte de dialogue qui s’ouvre, cliquez sur le bouton Implémenter.
L’objet source n°1 (le repère) est choisi par défaut car la figure ne contient qu’un seul repère.
Il vous est ensuite demandé de cliquer sur quatre points qui seront donc nos quatre points précédemment créés.
La courbe apparaît.
Enregistrez votre figure.
Pour finir nous allons enrichir cette figure en affichant la formule de la fonction polynôme en arrondissant les coefficients du polynôme à ${10}^{-2}$ près.
Créez quatre calculs a, b, c et d avec les formules ci-dessous (icône ![]() ) :
) :
– a’ : int(a*100+0.5)/100
– b’ : int(b*100+0.5)/100
– c’ : int(c*100+0.5)/100
– d’ : int(d*100+0.5)/100
puis utilisez l’icône ![]() pour créer une nouvelle fonction nommée f avec comme formule
pour créer une nouvelle fonction nommée f avec comme formule a'*x^3+b'*x^2+c'*x+d'.
Attention : Décochez la case Tracer courbe car la courbe existe déjà.
Pour afficher la formule de la fonction f, nous allons créer un affichage LaTeX dynamique.
Utilisez pour cela l’icône ![]() .
.
Cliquez en haut et à gauche de la figure et remplissez la boîte de dialogue ainsi :
- Cliquez sur le bouton Insertion de formule, sélectionnez la fonction f dans la liste et validez. Le code LaTeX suivant est alors inséré :
\ForSimp{f}. Compétez ce code pour avoirf(x)=\ForSimp{f} - Cochez la case Effacement du fond
- Validez
L’affichage LaTeX apparaît. Il est dynamique : la formule se modifie quand vous capturez les points A, B, C et D et elle est écrite toujours sous la forme la plus simple possible. Par exemple, si vous capturez C pour qu’il soit confondu avec l’origine O, le coefficient constant 0 n’apparaît plus.
Le code LaTeX utilise une fonction LaTeX spécifique à MathGraph32 : \ForSimp{}. Cette fonction remplace les valeurs des calculs utilisés par la formule et l’écrit sous une forme la plus simplifiée possible.
Voici la figure obtenue ci-dessous :
Le LaTeX
Nous allons ici montrer comment utiliser MathGraph32 pour réaliser la figure ci-dessous. Cette figure utilise un affichage LaTeX dynamique et des fonctions LaTeX internes au logiciel MathGraph32.
Le lecteur pourra aussi se référer à ce premier article et un second sur le site de MathGraph32.
Pour l’exemple ci-dessous il est conseillé d’utiliser la version 7.4.4 de MathGraph32 que vous pouvez télécharger sur cette page ou une version ultérieure.
Vous pouvez changer l’affixe du point dans le champ d’édition de z. Pour utiliser une racine carrée, utilisez la syntaxe rac() ou sqrt(). Si l’argument est remarquable (multiple de $\frac{\pi}{8}$ ou de $\frac{\pi}{12}$) il est écrit sous la forme d’une fraction de $\pi$.
Commencez par créer une nouvelle figure munie d’un repère orthonormal avec l’icône  (barre d’outils supérieure à gauche). Choisissez figure avec repère et choisissez un repère orthonormal en cochant la case Avec vecteurs.
(barre d’outils supérieure à gauche). Choisissez figure avec repère et choisissez un repère orthonormal en cochant la case Avec vecteurs.
 .
.
Par défaut les noms des vecteurs sont i et j. Ils sont affichés via des affichages LaTeX.
Pour les modifier, cliquez sur l’icône  de la barre supérieure (modification des objets graphiques créés via une boîte de dialoge).
de la barre supérieure (modification des objets graphiques créés via une boîte de dialoge).
Cliquez sur l’affichage LaTeX affichant i. Une boîte de dialogue s’ouvre. Remplacez le code LaTeX \vec{i} par \vec{u} et validez.
Cliquez sur l’affichage LaTeX affichant j. Remplacez de même le code LaTeX \vec{j} par \vec{v} et validez.
Vous pouvez maintenant activer la couleur bleue dans la palette des couleurs et cliquer sur le vecteur $\vec{i}$ et l’affichage LaTeX correspondant en vert.
Procédez de même avec du rouge pour le vecteur $\vec{j}$
Vérifiez à l’aide de l’icône  (barre supérieure, options de la figure) que l’unité de la figure est le radian.
(barre supérieure, options de la figure) que l’unité de la figure est le radian.
Utilisez l’icône 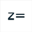 (Troisième rangée d’icônes à partir du bas) pour créer un calcul complexe nommé z avec comme formule
(Troisième rangée d’icônes à partir du bas) pour créer un calcul complexe nommé z avec comme formule 3+3*i.
Vous allez maintenant créer un éditeur de formules qui permettra de modifier sur la figure la valeur de z.
Pour cela, déroulez la barre d’icône des affichages, utilisez l’icône  , cliquez en haut et à gauche de la figure et remplissez la boîte de dialogue comme ci-dessous (les éditeurs de formule peuvent être déplacés avec l’outil de capture
, cliquez en haut et à gauche de la figure et remplissez la boîte de dialogue comme ci-dessous (les éditeurs de formule peuvent être déplacés avec l’outil de capture  en capturant leur en-tête).
en capturant leur en-tête).

Nous allons maintenant créer un point d’affixe z dans notre repère.
Utilisez pour cela l’icône  .
.
Dans la boîte de dialogue qui s’ouvre, entrez z dans le champ Affixe du point et validez.
Nous allons maintenant créer un affichage LaTeX lié à ce point avec l’outil  .
.
Cliquez d’abord sur le point créé puis remplissez la boîte de dialogue comme ci-dessous :

Vous pouvez ensuite déplacer cet affichage LaTeX avec l’outil 
Déroulez la barre des calculs, cliquez à sa droite sur l’icône  qui fournit des outils supplémentaires et choisissez l’item Partie réelle. Remplissez la boîte de dialogue comme ci-dessous (cette partie réelle sera nommée a).
qui fournit des outils supplémentaires et choisissez l’item Partie réelle. Remplissez la boîte de dialogue comme ci-dessous (cette partie réelle sera nommée a).

Déroulez de nouveau la barre des calculs, cliquez à sa droite sur l’icône  et choisissez l’item Partie imaginaire. Sélectionnez z dans la liste et choisissez comme nom b.
et choisissez l’item Partie imaginaire. Sélectionnez z dans la liste et choisissez comme nom b.
Déroulez la barre d’outils des points et utilisez l’outil  pour créer un point de coordonnées (a,0) et un point de coordonnées (0,b).
pour créer un point de coordonnées (a,0) et un point de coordonnées (0,b).
Dans la palette de style de trait, activez le style de trait pointillé, et joignez les deux derniers points créés au point M avec l’outil segment 
Déroulez la barre des calculs, cliquez à sa droite sur l’icône  et choisissez l’item Argument principal. Sélectionnez z dans la liste et choisissez comme nom argz.
et choisissez l’item Argument principal. Sélectionnez z dans la liste et choisissez comme nom argz.
Déroulez la barre des calculs, cliquez à sa droite sur l’icône  et choisissez l’item Module. Sélectionnez z dans la liste et choisissez comme nom modz.
et choisissez l’item Module. Sélectionnez z dans la liste et choisissez comme nom modz.
Avec l’outil  créez un calcul nommé q1 contenant comme formule
créez un calcul nommé q1 contenant comme formule argz/(pi/8).
Nous allons maintenant créer un calcul q’1 qui contiendra l’entier le plus proche de q1.
Utilisez de nouveau l’outil  pour créer un calcul nommé q’1 contenant comme formule
pour créer un calcul nommé q’1 contenant comme formule int(q1+0.5).
De même créez un calcul nommé q2 contenant comme formule argz/(pi/12) et un calcul nommé q’2 contenant comme formule int(q2+0.5).
Créez maintenant les calculs suivants :
– g1 contenant comme formule pgcd(abs(q'1),8)
– n1 contenant comme formule q'1/g1
– d1 contenant comme formule 8/g1
– g2 contenant comme formule pgcd(abs(q'2),12)
– n2 contenant comme formule q'2/g1
– d2 contenant comme formule 12/g2
Les fonctions que nous allons maintenant créer nous serviront à créer un affichage LaTeX particulier.
Utilisez l’icône  pour créer une fonction nommée f1 comme ci-dessous en n’oubliant pas de décocher la case Tracer courbe.
pour créer une fonction nommée f1 comme ci-dessous en n’oubliant pas de décocher la case Tracer courbe.
Voici la formule à entrer : n1*pi/d1

De même créer une fonction nommée f2 comme ci-dessous en n’oubliant pas de décocher la case Tracer courbe.
Voici la formule à entrer : n2*pi/d2

Nous allons créer un premier affichage LaTeX libre chargé d’afficher une valeur approchée du module de z : Déroulez la barre des affichages, utilisez l’icône  et cliquez en haut et à gauche de la figure, au-dessous de l’éditeur de formules.
et cliquez en haut et à gauche de la figure, au-dessous de l’éditeur de formules.
Dans le champ Code Latex entrez |z| = |\text{OM}| \approx \Val{modz,3} et cochez la case Effacement du fond.
Le code \approx peut lui être obtenu en cliquant le caractère correspondant dans la boîte de dialogue flottante (onglet Maths).
Le code \Val{modz,3} peut être obtenu en cliquant sur le bouton Insertion de valeur dynamique en demandant 3 décimales. Il provoque l’affichage approché de modz avec 3 décimales.
Avant de créer l’affichage laTeX suivant, nous allons créer une fonction et deux calculs.
Utilisez l’icône ![]() pour créer une fonction nommée zero comme ci-dessous en n’oubliant pas de décocher la case Tracer courbe.
pour créer une fonction nommée zero comme ci-dessous en n’oubliant pas de décocher la case Tracer courbe.
Voici le contenu du champ Formule : abs(x)<0.000000001

Maintenant utilisez l’icône  pour créer deux calculs :
pour créer deux calculs :
– Un calcul nommé test1 contenant comme formule zero(q1-q'1)
– Un calcul nommé test2 contenant comme formule zero(q2-q'2)
Ces deux calculs nous servent à savoir si les nombres contenus dans q1 et q2 sont entiers (en évitant les erreurs d’arrondi).
Utilisez l’icône  et cliquez en haut et à gauche de la figure, au-dessous de l’affichage précédent.
et cliquez en haut et à gauche de la figure, au-dessous de l’affichage précédent.
Voici le code LaTeX à entrer :
\If {test1}
{
\theta = arg(z) = \ForSimp{f1} \left[ 2\pi \right]
}
{
\If{test2}
{
\theta = arg(z) = \ForSimp{f2} \left[ 2\pi \right]
}
{
\theta = arg(z) \approx \Val{argz,3}\; rad
}
}Quelques explications concernant ce code LaTeX :
Le code \If est spécifique à MathGraph32 : La syntaxe est \If{calcul}{Affichage si calcul = 1}{Affichage sinon}
Ainsi, si q1 est un nombre entier, on affichera la formule de la fonction f1, ce qui provoquera un affichage d’une fraction de $\pi$ quand l’argument est un multiple de $\frac{\pi}{8}$, sinon, si q2 est un nombre entier, on affichera la formule de f2 qui provoquera un affichage d’une fraction de $\pi$ quand l’argument est un multiple de $\frac{\pi}{12}$ et dans les autres cas on affichera une valeur approchée de argz avec 3 décimales, suivi de rad.
A noter que le code \ForSimp{f1}} provoque un affichage simplifié de la formule contenue dans f1, en éliminant les multiplications ou divisions par 1 et les additions de 0. Ainsi, dans le cas où, par exemple, n1 = 1 et d1 = 4, le résultat affiché sera $\frac{\pi}{4}$ et non pas $\frac{1 \times \pi}{4}$.
Complétons la figure :
– Utilisez l’icône  pour joindre le point O au point M par un segment (Choisir avant la couleur marron et un trait continu avec une épaisseur de 3 pixels par exemple).
pour joindre le point O au point M par un segment (Choisir avant la couleur marron et un trait continu avec une épaisseur de 3 pixels par exemple).
– Utilisez l’icône  pour créer une marque d’angle orienté en cliquant dans l’ordre sur le point I (sur l’axe des abscisse), le point O et le point M (Choisir avant la couleur rouge et un trait continu avec une épaisseur de 2 pixels par exemple). Les icônes de marques de segment ou d’angle figurent dans la sixième barre d’icônes à partir du haut).
pour créer une marque d’angle orienté en cliquant dans l’ordre sur le point I (sur l’axe des abscisse), le point O et le point M (Choisir avant la couleur rouge et un trait continu avec une épaisseur de 2 pixels par exemple). Les icônes de marques de segment ou d’angle figurent dans la sixième barre d’icônes à partir du haut).
– Utilisez l’icône  pour créer la bissectrice de l’angle IOM.
pour créer la bissectrice de l’angle IOM.
– Utilisez l’icône  pour créer un point lié à cette bissectrice, au-dessus de la marque d’angle.
pour créer un point lié à cette bissectrice, au-dessus de la marque d’angle.
– Utilisez l’icône  pour créer un affichage LaTeX lié à ce dernier point comme ci-dessous (pour obtenir le code LaTeX pour la lettre $\theta$ vous pouvez utiliser la petite boîte de dialogue à droite) :
pour créer un affichage LaTeX lié à ce dernier point comme ci-dessous (pour obtenir le code LaTeX pour la lettre $\theta$ vous pouvez utiliser la petite boîte de dialogue à droite) :

Maintenant utilisez l’outil  pour masquer la bissectrice et le point lié.
pour masquer la bissectrice et le point lié.
Pour finir nous allons créer trois macros chargées de montrer ou masquer l’affichage de module et de l’argument.
Déroulez la barre d’outil des affichages, à sa droite, cliquez sur l’icône  et choisissez l’item Macro d’apparition.
et choisissez l’item Macro d’apparition.
Cliquez en haut et au milieu de la figure (endroit où sera affiché l’intitulé de la macro) et remplissez la boîte de dialogue comme ci-dessous (cliquez sur l’ellipse pour choisir la couleur de fond d’affichage) :
Voici le code de l’intitulé : $\text{Voir } |z|$

Cliquez ensuite sur l’affichage LaTeX du module de z puis cliquez sur le bouton rouge  pour indiquer que vous avez fini de désigner les objets que la macro doit faire apparaître). La macro apparaît sur la figure.
pour indiquer que vous avez fini de désigner les objets que la macro doit faire apparaître). La macro apparaît sur la figure.
A remarquer que l’intitulé étant encadré par des caractères $, il sera affiché en style LaTeX.
A la droite de l’intitulé de la macro précédente, créez une nouvelle macro d’apparition d’objets comme ci-dessous puis cliquez sur l’affichage LaTeX de l’argument de z.
Voici le code de l’intitulé : $\text{Voir }arg(z)$

Enfin déroulez la barre d’outil des affichages, à sa droite, cliquez sur l’icône  et choisissez l’item Macro de masquage.
et choisissez l’item Macro de masquage.
Cliquez à droite des deux dernières macros et remplissez la boîte de dialogue comme ci-dessous.
Voici le code de l’intitulé : $\text{Cacher}$

Cliquez ensuite sur les deux affichages LaTeX du module et de l’argument puis clic sur le bouton rouge  pour finir.
pour finir.
La figure est terminée.
L’export en html
Via l’icône  MathGraph32 permet d’exporter une figure dans une page html, via une bibliothèque écrite en JavaScript (choisir l’item Exporter en html).
MathGraph32 permet d’exporter une figure dans une page html, via une bibliothèque écrite en JavaScript (choisir l’item Exporter en html).
Toutes les figures dynamiques insérées dans cet article utilisent cette bibliothèque et les balises citées plus bas.
Au contraire des autres logiciels de géométrie dynamique (à ma connaissance), l’exportation se fait dans un SVG, c’est à dire en vectoriel. Ceci permet de garder une qualité irréprochable d’affichage quand on zoome sur périphérique mobile, par exemple.
Lorsqu’une figure ne s’affiche pas correctement, essayez de vider le cache de votre navigateur car il se peut que le défaut ait été corrigé mais que votre navigateur utilise une version précédente qu’il a mise en cache.
Les figures MathGraph32 insérées dans une page html sont décrites dans une grande chaîne de caractères (Base 64).
Pour obtenir le code Base64 d’une figure ouverte dans MathGraph32, utilisez l’icône  et choisissez l’item Obtenir le code base64 de la figure.
et choisissez l’item Obtenir le code base64 de la figure.
Lorsque vous voulez récupérer le code base64 d’une figure contenue dans une page html, demandez au navigateur d’afficher le code source de la page et copiez cette chaîne dans le presse-papier. Démarrez ensuite MathGraph32 et utilisez l’icône  , choisissez l’item Figure par code Base64 et collez cette chaîne dans le champ Code Base64 de la figure.
, choisissez l’item Figure par code Base64 et collez cette chaîne dans le champ Code Base64 de la figure.
Par exemple la chaîne ci-dessous contient le début du code d’une figure vierge munie d’un repère orthonormal (la chaîne complète ne peut pas être affichée dans cet article) :
TWF0aEdyYXBoSmF2YTEuMAAAAA8+TMzNAANmcmH###8BAP8BAAAAAAAAAAAHrwAABPUAAAAAAAAAAAAAAAEAAAAy#####
Pour insérer une figure dynamique MathGraph32 dans une page html, le plus plus simple est d’utiliser une balise.
Il y a deux types de balise :
Pour afficher une figure dynamique sur laquelle on peut agir mais pas la modifier :
Pour afficher une figure que l’on peut modifier en ligne :
Les paramètres width et height indiquent la largeur et la hauteur en pixels de la figure.
Le paramètre fig doit contenir le code Base64 de la figure à afficher.
Pour en savoir sur ces balises regardez cet article :
Pour en savoir plus sur l’exportation html vous pouvez vous référer à cette page.
MathGraph32 et Sesamath
Après avoir été un projet soutenu par Sesamath, MathGraph32 est devenu un projet à part entière de l’association il y a deux ans.
Via son moteur en JavaScript, MathGraph32 intervient dans de nombreuses ressources Sesamath :
– Plusieurs centaines de figures dynamiques sur les manuels numériques de seconde, première S et terminale S (certaines ne sont accessibles que pour le professeur qui doit se connecter avec son code Sesaprof).
– Des exercices interactifs LaboMep utilisent aussi ce moteur JavaScript en utilisant des figures dynamiques ou en utilisant certaines fonctions avancées de MathGraph32 permettant de savoir si l’élève a entré sa réponse sous la forme demandée. Il est ainsi possible de créer des exercices d’apprentissage, notamment de calcul.
– L’exportation des figures en LaTeX-Tikz permet de créer des pas-à pas en PDF permettant de dévoiler pas à pas la solution d’un exercice.
Exercices de calcul
MathGraph32 permet, via les ressources de l’association Sesamath, de mettre en ligne des exercices de calcul et de construction géométriquel.
Voici ci-dessous des liens vers des tutoriels LaboMep montrant comment créer de telles ressources dans LaboMep :
Voici des liens vers des tutoriels sur la création d’exercices en se basant sur une figure MathGraph32 :
Créer un exercice de construction avec correction
Créer un exercice de construction paramétrable avec correction
Créer un exercice de calcul géométrique avec test d’égalités intermédiaires
Créer un exercice de calcul : Exemple 1 sur les puissances
Créer un exercice de calcul : Exemple 2 sur produit de deux nombres complexes
Créer un exercice de calcul : Exemple 3 sur le calcul d’une intégrale
Créer un exercice de validation interne à une figure MathGraph32
Créer un exercice avec des éditeurs de formules et des listes déroulantes
Créer un exercice multi-éditeurs sur les puissances de 10
Créer un exercice de calcul en plusieurs étapes : Exemple de calcul d’une intégrale
Créer un exercice de calcul en plusieurs étapes : Exemple de calcul de dérivée avec listes déroulantes en formules LaTeX
Créer un exercice avec des phrases à trou
Créer un exercice de résolution d’équation à solutions multiples
Créer un exercice de résolution d’inéquation en une étape
Créer un exercice de calcul vectoriel (1)
Créer un exercice de calcul vectoriel (2)
Créer un exercice de construction avec possibilité de voir la figure faite par l’élève dans le bilan
Exemples d’exercices en ligne
Voici des exercices en ligne sur le site de MathGraph32 via l’outil j3p de Sesamath (qui doivent s’ouvrir dans un nouvel onglet de votre navigateur) :
La plupart de ces exercices sont disponibles dans LaboMep.
Résolution d’équations du premier degré
Résolution d’inéquations du premier degré
Exercices de calcul formel (qui conviennent aussi en classe de première).
Exercices sur les équations de droites (les deux derniers sont des exercices de transformation d’équation cartésienne en équation réduite)
Exercices de réduction au même dénominateur
Exercices sur les dérivées (niveau première)
Introduction sur un exemple des outils offerts par MathGraph32 pour créer des exercices de calcul
Voici un des ces exercices de calcul de dérivée en première. Il doit démarrer dans un nouvel onglet de votre navigateur.
Il s’agit de demander à l’élève de calculer la dérivée de la fonction f définie par f(x)=ax+b+c/x.
Il est spécifié dans le texte qu’il doit donner la dérivée sous forme réduite au même dénominateur, simplifiée au maximum.
Quand l’élève appuie sur la touche Entrée, sa réponse est évaluée.
Si sa réponse est incorrecte sur le plan syntaxique, sa réponse est affichée en rouge et il a droite à un nouvel essai (le nombre d’essais est paramétrable dans la ressource).
Si la réponse est correcte, elle s’affiche en bleu. S’il estime avoir donné la dérivée sous la forme demandée il doit cliquer sur le bouton OK (le nombre maximum de validations est aussi paramétrable).
S’il pense qu’il a fini l’exercice, il doit valider en cliquant sur le bouton OK à droite.
Voici ci-dessous un aperçu de la figure qui va permettre de générer cette exercice :
Dans cette figure nous voyons en haut un premier l’affichage LaTeX contenant ce qui sera l’énoncé (qui aura ici 2 lignes) et, au-dessous, un autre affichage LaTeX qui fournira la solution (qui aura ici 5 lignes).
Au-dessous, deux éléments qui ne serviton ici qu’à montrer comment fonctionne la figure :
Un éditeur de formule de la fonction rep (qui contiendra la réponse de l’élève).
Un affichage de la valeur du calcul reponse.
Si, par exemple, vous entrez dans le champ d’édition 5-5/x² vous voyez que la valeur de reponse est 2 : La réponse est bonne mais n’a pas été réduite au même dénominateur.
Si vous entrez une réponse fausse, la valeur de reponse sera 0.
Si vous entrez comme réponse 35(x²-1)/x², reponse vaut 1 ce qui correspond à une réponse exacte et écrite sous une des formes attendues.
Montrons quelques étapes pour construire une figure de ce type.
Pour l’exemple ci-dessous il est conseillé d’utiliser la version 7.4.4 de MathGraph32 que vous pouvez télécharger sur cette page ou une version ultérieure.
Démarrez MathGraph32 et utilisez l’icône  pour créer une nouvelle figure sans repère et sans longueur unité.
pour créer une nouvelle figure sans repère et sans longueur unité.
Utilisez l’icône  pour créer une variable k comme ci-dessous.
pour créer une variable k comme ci-dessous.

Utilisez l’icône  de création d’un calcul pour créer les calculs suivants :
de création d’un calcul pour créer les calculs suivants :
| Nom du calcul | Formule | Commentaire |
| nbvar | 6 | Il y a dans cet exercice 6 entiers aléatoires à utiliser |
| nbcas1 | 2 | Lors de la réalisation de l’exercice il sera donné à r1 des valeurs entre 0 et nbcas1, sans avoir deux fois la même valeur lors des répétitions successives. |
| nbcas2 | 5 | Lors de la réalisation de l’exercice il sera donné à r2 des valeurs entre 0 et nbcas1, sans avoir deux fois la même valeur lors des répétitions successives. |
| nbcas3 | 2 | Lors de la réalisation de l’exercice il sera donné à r3 des valeurs entre 0 et nbcas1, sans avoir deux fois la même valeur lors des répétitions successives. |
| nbcas4 | 5 | Lors de la réalisation de l’exercice il sera donné à r4 des valeurs entre 0 et nbcas1, sans avoir deux fois la même valeur lors des répétitions successives. |
| nbcas5 | 2 | Lors de la réalisation de l’exercice il sera donné à r5 des valeurs entre 0 et nbcas1, sans avoir deux fois la même valeur lors des répétitions successives. |
| nbcas6 | 2 | Lors de la réalisation de l’exercice il sera donné à r6 des valeurs entre 0 et nbcas1, sans avoir deux fois la même valeur lors des répétitions successives. |
| r1 | int(rand(0)*nbcas1) | Sert à simuler les valeurs qui seront affectées à r1 lors des répétitions de l’exercice |
| r2 | int(rand(0)*nbcas2) | Sert à simuler les valeurs qui seront affectées à r2 lors des répétitions de l’exercice |
| r3 | int(rand(0)*nbcas3) | Sert à simuler les valeurs qui seront affectées à r3 lors des répétitions de l’exercice |
| r4 | int(rand(0)*nbcas4) | Sert à simuler les valeurs qui seront affectées à r4 lors des répétitions de l’exercice |
| r5 | int(rand(0)*nbcas5) | Sert à simuler les valeurs qui seront affectées à r5 lors des répétitions de l’exercice |
| r6 | int(rand(0)*nbcas6) | Sert à simuler les valeurs qui seront affectées à r1 lors des répétitions de l’exercice |
| a | (-1)^r1*(r2+1) | a prendra des valeurs positives ou négatives, de valeur absolue comprise entre 1 et 5 |
| b | (-1)^r3*(r4+1) | b prendra des valeurs positives ou négatives, de valeur absolue comprise entre 1 et 5 |
| c | (-1)^r5*(r6+1) | c prendra des valeurs positives ou négatives, de valeur absolue comprise entre 1 et 5 |
| g | pgcd(abs(a),abs(c)) | g contiendra le PGCD des valeurs absolues de a et de c |
Maintenant utilisez l’icône  pour créer les fonctions de la variable réelle x suivantes :
pour créer les fonctions de la variable réelle x suivantes :
| Nom de la fonction | Formule | Commentaire |
| zero | abs(x)<0.000000001 | Renvoie 1 si la valeur absolue de l’argument est inférieure à 0,000000001 près |
| entier | zero(x-int(x)) | Renvoie 1 si la nombre est proche de sa partie entière à 0,000000001 près |
| rep | 0 | Morsque la figure communiquera avec Labomep, il sera affecté à rep la formule entrée par l’élève. |
| f | a*x+b+c/x | Sert à afficher la formule de la fonction à dériver dans l’énoncé |
| sol | (a*x^2-c)/x^2 | Sert dans l’affichage détaillé de la solution. |
| f’ | a-c*(1/x^2) | Sert à vérifier si la réponse de l’élève est exacte et lors de la correction. |
| form1 | a*x^2/x^2-c/x^2 | Sert lors de l’affichage de la correction. |
| foru | a*x+b | Sert lors de l’affichage de la correction. |
| forv | x | 1/x |
Pour l’affichage de la correction nous utiliserons aussi deux fonctions de deux variables.
Déroulez la barre d’outil des calculs et, à sa droite, cliquez sur l’icône  . Choisissez l’item Fonction réelle de deux variables et remplissez la boîte de dialogue comme ci-dessous :
. Choisissez l’item Fonction réelle de deux variables et remplissez la boîte de dialogue comme ci-dessous :

Voici ce qui est utilisé pour la formule de cette fonction : u+c*v.
Recommencez pour créer une autre fonction de deux variables comme ci-dessous (cette fois les noms des variables sont u’ et v’) :

Utilisez de nouveau l’icône  de création d’un calcul pour créer les calculs suivants :
de création d’un calcul pour créer les calculs suivants :
| Nom du calcul | Formule | Commentaire |
| test | entier(g/k) | Vaudra 1 si g est divisible par la variable k et 0 sinon. |
| a’ | a/k | |
| c’ | c/k | |
| x1 | rac(2)+rand(0) | Nombre aléatoire utilisé pour tester si la réponse de l’élève est exacte |
| x2 | rac(3)+rand(0) | Nombre aléatoire utilisé pour tester si la réponse de l’élève est exacte |
| x1 | rac(7)+rand(0) | Nombre aléatoire utilisé pour tester si la réponse de l’élève est exacte |
| exact | zero(f’(x1)-rep(x1))&zero(f’(x2)-rep(x2))&zero(f’(x3)-rep(x3)) | Vaudra 0 si la réponse de l’élève est exacte. |
Dans la consigne nous allons demander à l’élève de calculer f’(x) sous la forme d’un quotient écrit le plus simplement possible.
Si $f(x)=6x+1-\frac{6}{x}$ nous accepterons comme réponse finale $\frac{6x^2+1}{6x^2}$ mais aussi $\frac{6(x^2+1)}{x^2}$, $\frac{3(2x^2+2)}{x^2}$ et $\frac{2(3x^2+3)}{x^2}$.
Créez maintenant avec l’icône  les deux fonctions de la variable réelle x suivantes :
les deux fonctions de la variable réelle x suivantes :
| Nom de la fonction | Formule | Commentaire |
| sol1 | k*(a’*x^2-c’)/x^2 | Va servir à vérifier si la réponse de l’élève est une des formules finales attendues. |
| sol2 | -k*(c’-a’*x^2)/x^2 | Va servir à vérifier si la réponse de l’élève est une des formules finales attendues. |
Nous allons maintenant créer des calculs très spéciaux que MathGraph32 prend en charge (et, à ma connaissance est le seul logiciel à le faire) : les test d’équivalence.
Déroulez la barre des calculs et, à sa droite, cliquez sur l’icône  . Choisissez ensuite l’item Test d’équivalence.
. Choisissez ensuite l’item Test d’équivalence.
Une boîte de dialogue s’ouvre . Remplissez là comme ci-dessous :

Voici comment fonctionne ce test d’équivalence :
– Si le calcul test n’est pas égal à 1 (donc si g n’est pas divisible par k) il renvoie 0.
– Si le calcul test est égal à 1 (donc si g est divisible par k) il commence par remplacer dans la fonction sol1 les calculs k, a’ et c’ par leurs valeurs, simplifie ensuite les multiplications ou divisions par 1, les additions de 0, et compare ensuite la formule obtenue à cette de la fonction rep en regardant si elles sont équivalentes au point de vue algébrique (compte-tenu de la commutativité de l’addition et de la multiplication). Il renvoie comme valeur 1 s’il y a équivalence et 0 sinon.
– Créez de même un nouveau test d’équivalence de calculs pour créer un test d’équivalence entre sol2 et rep comme indiqué ci-dessous :

La solution proposée par l’élève sera considérée comme bonne si, pour les valeurs de k variant de 1 à g, la fonction rep est équivalente à sol1 ou sol2, ce qui revient à accepter les formes factorisées par une constante pour le numérateur (constante positive ou négative).
Déroulez la barre des calculs et, à sa droite, cliquez sur l’icône  . Choisissez ensuite l’item Somme indicée.
. Choisissez ensuite l’item Somme indicée.
Remplissez la boîte de dialogue comme ci-dessous :

Ainsi, si un des tests d’équivalence est égal à 1 pour une valeur de k divisant g, notre somme S1 ne sera pas nulle.
De même créez une deuxième somme indicée comme ci-dessous :

Créez maintenant un calcul nommé resolu avec comme formule S1>0|S2>0.
L’opérateur | est le OU logique. resolu vaudra 1 si au moins un des deux calculs S1 ou S2 est égal à 1.
Pour finir, créez un calcul nommé reponse qui contiendra la formule suivante : si(resolu,1,si(exact,2,0)).
Ainsi, reponse vaudra 1 si la réponse de l’élève est bonne et si elle est donnée sous une forme acceptée, 2 si le calcul est exact mais considéré comme pas terminé et 0 sinon.
Pour que cet exercice soit complet il faut ensuite pourvoir afficher une correction dans un affichage Nous allons maintenant créer un affichage LaTeX chargé de fournir à LaboMep les lignes à afficher pour la consigne.
Déroulez la barre des affichages et utilisez l’icône  (affichage LaTeX libre).
(affichage LaTeX libre).
Cliquez en haut et à gauche de la figure et remplissez la boîte de dialogue comme ci-dessous :

Voici le code LaTeX à utiliser :
Pour créer cet affichage LaTex, on commence par utiliser le bouton  qui insère le code pour un tableau à deux lignes.
qui insère le code pour un tableau à deux lignes.
Chacune des lignes devra être un champ \text{} donc le contenu sera la première ligne de la consigne (utilisez le bouton  ).
).
A l’intérieur de ce \text{} on encadre de $ ce qui doit être affiché en mode Maths.
Pour obtenir le code \ForSimpf, cliquez sur le bouton Insertion de formule, sélectionnez f dans la liste et validez. Ce code insère le code LaTeX correspondant à la formule de la fonction f en remplaçant les valeurs de a, b et c par leurs valeurs et en supprimant les additions de 0, les produits ou quotients par 1 entre autres.
Une fois cet affichage LaTeX créé, nous allons lui affecter un tag de valeur enonce.
Pour cela, dans la barre d’outil supérieure, activez l’outil  (protocole de la figure).
(protocole de la figure).
Déroulez vers le bas la liste d’objets de gauche et sélectionnez l’affichage LaTeX que nos venons de créer.
Cliquez ensuite à droite sur le bouton Changer le tag et, dans la boîte de dialogue qui s’ouvre, entrez le Tag solution puis validez.
Ainsi, quand notre figure dialoguera avec LaboMep, cet affichage LaTeX sera repéré comme à utiliser pour afficher la consigne de l’exercice.
Nous allons maintenant créer un autre affichage LaTeX qui sera chargé, lui de fournir les lignes de la correction de cet exercice.
Déroulez de nouveau la barre des affichages et utilisez l’icône  (affichage LaTeX libre).
(affichage LaTeX libre).
Cliquez au-dessous de l’affichage LaTeX précédent. Une boîte de dialogue s’ouvre comme précédemment.
Voici le code LaTeX à utiliser :
Ainsi notre correction sera constituée de cinq lignes qui sont le contenu des cinq \text{} de notre code laTeX.
Pour obtenir par exemple le code LaTeX pour une fraction \dfrac-1 x^2 on eut utiliser le bouton 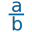 .
.
Une fois cette boîte de dialogue validée, réactivez l’outil de protocole  et affectez à cet affichage LaTeX le tag solution.
et affectez à cet affichage LaTeX le tag solution.
Enregistrez votre figure dans le dossier de votre choix.
Comment utiliser notre figure pour créer un nouvel exercice dans LaboMep :
Démarrez LaboMep et connectez-vous.
A droite, déroulez Mes Ressources, et faites un clic droit sur un dossier contenu dans Mes Ressources. Dans l’exemple ci-dessous, il s’agit du dossier Test. Si vous n’avez pas de dossier dans Mes Ressources, vous devez en créer un (en cliquant droit sur l’icône avec un dossier et un signe + vert).

Cliquez sur l’item de menu Créer une ressource.
Au centre de la fenêtre apparaît un nouvel onglet Nouvelle ressource et une page avec des éléments à compléter.
Dans le champ Titre, entrez Dérivée de ax+b+c/x.
Dans le champ Type technique, choisissez activité j3p.
Dans Catégories, cochez la case Exercice interactif.
Dans Niveau, cochez les cases seconde et première.
Dans les champs Résumé et Description, entrez Demande de calculer la dérivée de ax+b+c/x et de l’écrire sous la forme d’un quotient.
En bas de la page, cliquez sur Enregistrer.
Apparaît alors en bas de la page un éditeur de graphe.
Vous pouvez donner plus de place à l’arbre de gauche en faisant glisser la barre de séparation entre les deux parties de l’éditeur de graphe. Vous pouvez aussi passer en mode plein écran pour l’éditeur de graphe.
Dans l’arbre de gauche, déroulez le nœud Composants MathGraph32 pour j3p.
Ensuite faites glisser Exercice de calcul MathGraph32 avec éditeur externe dans l’éditeur de graphe.
Un nœud apparaît (Nœud 1).
Faites un clic droit sur Nœud 1 et choisissez Paramétrage.
Dans le champ Titre entrez ce qui suit :Dérivée de ax+b+c/x. Ce titre sera affiché en haut de la fenêtre de l’exercice.
Le champ fig doit contenir le code Base64 de la figure que nous avons préparée précédemment.
Si nécessaire, rouvrez la figure et utilisez l’icône  d’exportation de la barre d’outils supérieure et choisissez Obtenir le code Base64 de la figure. Si vous utilisez la version autonome de MathGraph32, un message vous prévient que le code Base 64 a été copié dans le presse-papier. Sinon une boîte de dialogue apparaît vous présentant ce code dans un champ d’édition dont vous devez copier le contenu dans le presse-papier.
d’exportation de la barre d’outils supérieure et choisissez Obtenir le code Base64 de la figure. Si vous utilisez la version autonome de MathGraph32, un message vous prévient que le code Base 64 a été copié dans le presse-papier. Sinon une boîte de dialogue apparaît vous présentant ce code dans un champ d’édition dont vous devez copier le contenu dans le presse-papier.
Collez le contenu du presse-papier dans le champ fig (il s’agit d’une très grosse chaîne de caractères commençant par les caractères TWF0a). Cette chaîne a été fournie en haut de cet article.
Dans le champ nbrepetitions, entrez 2.
Dans le champ param, entrez abc (nous pourrons imposer une valeur pour a, b ou c).
Dans le champ nomCalcul mettez : f’(x)=. C’est ce qui sera affiché devant l’éditeur de formule.
Ne cochez pas case Validation Auto.
Dans ce mode l’élève a droit à nbEssais calculs intermédiaires (qu’il fait en appuyant sur la touche Entrée) et à nbchances validations (qu’il fait en cliquant sur le bouton OK uand il estime que sa formule répond à la question posée.
Dans le champ nbEssais entrez par exemple 6 et, dans le champ nbchances, entrez 2.
Le champ nblatex correspond à d’anciennes ressources et n’a plus à être utilisé (l’énoncé est fourni par l’affichage LaTeX de tag enonce).
Le champ indicationfaute ne sera pas utilisé ici.
Dans le champ charset entrez la chaîne suivante : x\d+-*/()^²., (ce sont les caractères autorisés à la frappe dans l’éditeur, \d représentant tous les chiffres). Vous pouvez aussi utiliser x0123456789+-*/()^².,
Si vous voulez maintenant tester votre ressource, fermez d’abord l’onglet Dérivée de ax+b+c/x puis, dans Mes Ressources, faites un clic droit sur la ressource Dérivée de ax+b+c/x et choisissez Tester la ressource.
Vous pouvez maintenant tester la ressource : Un exercice de calcul de calcul de la dérivée doit vous être proposé deux fois de suite avec des valeurs différentes de n.
A remarquer : Si vous dupliquez cette ressource, vous pourrez par exemple imposer une valeur donnée pour a, b et c. Il suffira de cliquer droit sur le noeud de la ressource, et, en bas, d’entrer la valeur que vous souhaitez pour a, b ou c (par exemple b=0 pour la dérivée de ax+c/x).
J’invite des lecteurs qui seraient intéressés par la création de tels exercices à se rapprocher de l’association Sesamath.
Perspectives
La première version de cet article datait de 2017.
Il a été entièrement mis à jour en février 2023.
Depuis, MathGraph32 a beaucoup évolué, a été récrit en JavaScript, et il possède de nouvelles fonctionnalités (comme par exemple une prise en charge du calcul matriciel réel).
MathGraph32 est utilisé dans des centaines de ressources LaboMep et vous pouvez l’utiliser pour créer vos propres ressources LaboMep.
Vous pouvez faire des exercices se déroulant en plusieurs étapes, même faire des exercices de calcul intégral comme celui-ci : https://bibliotheque.sesamath.net/public/voir/5e7379d4d1d2d74c7d1b4271 ou des exercices de calcul vectoriel comme celui-ci : https://bibliotheque.sesamath.net/public/voir/5f4ba3fde8203801d02d5570
Si une de vos ressources vous semble bien aboutie, vous pouvez contacter Sésamath pour la proposer. Si elle est validée par nos testeurs elle enrichira la base de ressources de LaboMep.
Yves Biton.
Retour en haut de la page