N.D.L.R. Dans l’article que voici, Benjamin Clerc continue de passer en revue les algorithmes introduits par la réforme de 2019 des programmes de Lycée. Pour mémoire :
- Les algorithmes du programme 2019 de mathématiques de Seconde
- Les algorithmes du programme de spécialité mathématiques de Première (2019).
- Les algorithmes du programme de Mathématiques de Première technologique (2019).
- Mathématiques complémentaires : les algorithmes du programme de l’option de Terminale (2020)
- Les algorithmes du programme de l’option de Terminale « Mathématiques expertes » (2020)
Il convient d’y ajouter
- Cet article d’Alain Busser
- Et celui de Matthieu Brabant au sujet du Lycée Professionnel.
L’article qui suit a été complété et enrichi par les suggestions et l’apport de Cyrille Guieu.
Cet article peut être librement diffusé et son contenu réutilisé pour une utilisation non commerciale (contacter l’auteur pour une utilisation commerciale) suivant la licence CC-by-nc-sa.
Programme de spécialité de mathématiques de terminale générale (BO de l’Éducation Nationale)
Algèbre et géométrie
Pour un entier n donné, génération de la liste des coefficients $\begin{pmatrix} n\\ k \end{pmatrix}$ à l’aide de la relation de Pascal.
Le triangle de Pascal est une présentation des coefficients binomiaux dans un triangle. Il fut nommé ainsi en l’honneur du mathématicien français Blaise Pascal.
| 1 | ||||||||||
| 1 | 1 | |||||||||
| 1 | 2 | 1 | ||||||||
| 1 | 3 | 3 | 1 | |||||||
| 1 | 4 | 6 | 4 | 1 | ||||||
| 1 | 5 | 10 | 10 | 5 | 1 |
La construction du triangle suit la relation de Pascal :
$\begin{pmatrix}
n\\
k
\end{pmatrix} = \begin{pmatrix}
n - 1\\
k - 1
\end{pmatrix} + \begin{pmatrix}
n - 1\\
k
\end{pmatrix} $
Python possède une commande binomial du module Sympy (Installation du module Sympy en installant Anaconda) qui permet de calculer le coefficient binomial de deux entiers naturels :
>>> from sympy import binomial
>>> binomial(6,2)
15ou pour répondre à la commande :
>>> for k in range(7):
binomial(6,k)
1
6
15
20
15
6
1mais nous allons bien sûr créer une fonction qui donne la même chose, en utilisant le fait que :
$\begin{pmatrix}
n\\
n-k
\end{pmatrix} = \frac{n !}{(n-(n-k)) !(n-k) !}= \frac{n !}{k !(n-k) !} = \begin{pmatrix}
n\\
k
\end{pmatrix} $
def binomialp(n, p):
if p>n:
return(0)
if 2*p>n:
p=n-p
if p == 0:
return(1)
return(binomialp(n-1,p)+binomialp(n-1,p-1))
def binomial(n):
L=[]
for i in range(n+1):
L.append(binomialp(n,i))
return LUtilisation :
>>> binomialp(6,2)
15
>>> binomial(6)
[1, 6, 15, 20, 15, 6, 1]
>>> for i in range(6):
binomial(i)
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
[1, 5, 10, 10, 5, 1]En remarquant que :
$\begin{pmatrix}
n\\
k
\end{pmatrix} = \frac{n !}{(n-k) !k !} = \frac{n(n-1) !}{k((n-1)-(k-1)) !(k-1) !} = \frac{n}{k} \begin{pmatrix}
n - 1\\
k - 1
\end{pmatrix}$, ce qui permet d’utiliser une autre fonction récursive :
def binomialk(n, k):
if k > n:
return(0)
if 2*k > n:
k = n-k
if k == 0:
return(1)
return(n//k*binomialk(n-1,k-1))La solution ci-dessous n’utilise pas d’appel récursif d’une fonction et génère les coefficients par un affichage :
def binome(n):
pascal=[1]
print(pascal)
k=1
while k<=n:
k=k+1
pascal2=[1]
for i in range(1,k-1):
pascal2.append(pascal[i-1]+pascal[i])
pascal=pascal2
pascal.append(1)
print(pascal)Utilisation :
>>> binome(4)
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]Génération des permutations d’un ensemble fini, ou tirage aléatoire d’une permutation.
Python possède une commande permutations du module itertools qui permet de donner toutes les permutations possibles des éléments d’un ensemble :
>>> from itertools import permutations
>>> list(permutations(['a', 'b', 'c']))
[('a', 'b', 'c'), ('a', 'c', 'b'), ('b', 'a', 'c'), ('b', 'c', 'a'), ('c', 'a', 'b'), ('c', 'b', 'a')]Python possède également une fonction shuffle du module random qui permet d’obtenir une permutation aléatoire des éléments d’une liste :
>>> from random import shuffle
>>> L=[1,2,3,5]
>>> shuffle(L)
>>> L
[1, 3, 2, 5]mais nous allons bien sûr créer des fonctions qui donnent la même chose.
On prendra cet ensemble fini sous forme de liste et on utilisera les méthodes de listes :
- append() qui permet d’ajouter un élément à une liste, en bout de liste ;
- pop() qui permet d’extraire d’une liste un élément de rang donné.
La fonction randrange() du module random nous permettra de gérer le côté aléatoire du tirage (randrange a la même syntaxe que range).
On va extraire de la liste initiale, au hasard, les éléments un à un, que l’on va mettre dans une nouvelle liste qui constituera la permutation aléatoire de la liste prise en paramètre de la fonction.
from random import randrange def permutalea(L): sortie=[] for i in range(len(L)): sortie.append(L.pop(randrange(len(L)))) return sortieUtilisation :
>>> permutalea([4,1,2,8,7]) [8, 4, 2, 7, 1]Pour générer toutes les permutations, on peut utiliser la récursivité en créant un algorithme qui va boucler sur tous les termes de la liste mis en première position suivis des permutations du reste de la liste, soit :
def permutation(L): if len(L) == 0: return [] if len(L) == 1: return [L] sortie = [] for i in range(len(L)): m = L[i] ResteListe = L[:i] + L[i+1:] for p in permutation(ResteListe): sortie.append([m] + p) return sortieUtilisation :
>>> permutation([1,2,3,5]) [[1, 2, 3, 5], [1, 2, 5, 3], [1, 3, 2, 5], [1, 3, 5, 2], [1, 5, 2, 3], [1, 5, 3, 2], [2, 1, 3, 5], [2, 1, 5, 3], [2, 3, 1, 5], [2, 3, 5, 1], [2, 5, 1, 3], [2, 5, 3, 1], [3, 1, 2, 5], [3, 1, 5, 2], [3, 2, 1, 5], [3, 2, 5, 1], [3, 5, 1, 2], [3, 5, 2, 1], [5, 1, 2, 3], [5, 1, 3, 2], [5, 2, 1, 3], [5, 2, 3, 1], [5, 3, 1, 2], [5, 3, 2, 1]]
Génération des parties à 2, 3 éléments d’un ensemble fini
Python possède une commande combinations du module itertools qui permet de donner toutes les combinaisons possibles de m éléments d’un ensemble à n éléments :
>>> from itertools import combinations
>>> list(combinations([1,2,3,5,7],2))
[(1, 2), (1, 3), (1, 5), (1, 7), (2, 3), (2, 5), (2, 7), (3, 5), (3, 7), (5, 7)]
>>> list(combinations([1,2,3,5,7],3))
[(1, 2, 3), (1, 2, 5), (1, 2, 7), (1, 3, 5), (1, 3, 7), (1, 5, 7), (2, 3, 5), (2, 3, 7), (2, 5, 7), (3, 5, 7)]Il est à noter que l’on n’obtient pas toutes les permutations, on a (1,2) mais pas (2,1).
Si l’on programme cette fonction dans Python :
def generation_parties(L,m):
n=len(L)
if m>n:
return
elif m==2:
return {(a,b) for a in L for b in L if a!=b}
elif m==3:
return {(a,b,c) for a in L for b in L for c in L if a!=b!=c}Utilisation :
>>> generation_parties([1,2,3,5],2)
{(1, 2), (3, 2), (1, 3), (3, 1), (2, 1), (1, 5), (2, 3), (5, 3), (5, 1), (2, 5), (5, 2), (3, 5)}On obtient toutes les permutations, et si l’on veut un fonctionnement similaire à la fonction combinations d’itertools :
def generation_parties2(L,m):
n=len(L)
if m>n:
return
elif m==2:
return {(a,b) for a in L for b in L if a<b}
elif m==3:
return {(a,b,c) for a in L for b in L for c in L if a<b<c}Utilisation :
>>> generation_parties2([1,2,3,5],2)
{(1, 2), (1, 3), (1, 5), (2, 3), (2, 5), (3, 5)}Analyse
Recherche de seuils.
Commençons par une recherche de seuil pour une suite croissante définie par récurrence par $U_{n+1} = f(U_n)$ et un premier terme :
def seuil(f,M,u0):
n=0
u=u0
while u<=M:
n=n+1
u=f(u)
return nUtilisation :
>>> def f(u):
return u+50
>>> seuil(f,1000,100)
19Nous vous laissons adapter ce code pour le cas d’une suite décroissante.
Recherche de valeurs approchées de $\pi, e, \sqrt{2}, \frac{1 + \sqrt{5}}{2}, ln(2),$ etc.
Valeur approchée de 𝜋
Nous avons déjà approximé 𝜋 en classe de première avec la méthode d’Archimède et la méthode de Monte Carlo, nous utiliserons en Terminale la formule de Bellard :
$\displaystyle \pi ={\frac {1}{2^{6}}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2^{10n}}}\left(-{\frac {2^{5}}{4n+1}}-{\frac {1}{4n+3}}+{\frac {2^{8}}{10n+1}}-{\frac {2^{6}}{10n+3}}-{\frac {2^{2}}{10n+5}}-{\frac {2^{2}}{10n+7}}+{\frac {1}{10n+9}}\right)$
def bellard(n):
pi=0
for i in range(n+1):
pi+=(-2**5/(4*i+1)-1/(4*i+3)+2**8/(10*i+1)-2**6/(10*i+3)-2**2/(10*i+5)-2**2/(10*i+7)+1/(10*i+9)) *(-1)**i/(2**6*2**(10*i))
return piUtilisation :
>>> bellard(3)
3.1415926535897545
>>> bellard(4)
3.1415926535897922A noter que Python ne peut faire mieux que bellard(4) qui n’est pas une bonne approximation puisque les 3 dernières décimales sont erronées. En utilisant le module Decimal, on obtient deux décimales exactes de plus, pas plus ...
Valeur approchée de e
Une valeur approchée de e (nombre d’Euler, ou nombre Népérien) peut être calculée en utilisant la formule suivante :
$e \approx 1 + \frac{1}{1 !} + \frac{1}{2 !} + \frac{1}{3 !} + ... + \frac{1}{n !}$
Avec une fonction factorielle :
def factorielle(n):
if n==0:
return 1
else:
return n*factorielle(n-1)
def calcul_e(n):
if n==0:
return 1
else:
return calcul_e(n-1)+1/factorielle(n)Utilisation :
>>> calcul_e(2)
2.5
>>> calcul_e(3)
2.6666666666666665
>>> calcul_e(20)
2.7182818284590455Pour ceux qui préfèrent une version non récursive de la fonction factorielle :
def factorielle(n):
if n==0:
return 1
else:
resultat=1
for i in range(1,n+1):
resultat*=i
return resultatValeur approchée de $\sqrt{2}$
On doit à Théon de Smyrne ces deux suites $(p_n)$ et $(q_n)$ définies par récurrence :
$p_{n + 1} = p_n + 2q_n, p_0 = 1$ ;
$q_{n + 1} = p_n + q_n, q_0 = 1$.
Ces suites sont à valeur entière strictement positive, donc strictement croissantes par récurrence, et vérifient :
$p_n² − 2q_n² = (−1)^n(p_0² − 2q_0²)$ de sorte que $\frac{p_n}{q_n}$ tend vers $\sqrt{2}$.
def racine2(n):
p,q=1,1
for i in range(n):
p,q=p+2*q,p+q
return p/qUtilisation :
>>> racine2(10)
1.4142135516460548
>>> racine2(100)
1.4142135623730951Valeur approchée de $\frac{1 + \sqrt{5}}{2}$
La suite de Fibonacci $(Fn)$ est définie par récurrence :
$F_1 = F_2 = 1$ et $F_{n + 2} = F_{n + 1} + F_n$ .
Une de ses propriétés est que ${\displaystyle\varphi =\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}}$
def nombredor(n):
p,q=1,1
for i in range(n):
p,q=q,p+q
return q/pUtilisation :
>>> nombredor(10)
1.6179775280898876
>>> nombredor(20)
1.618033985017358
>>> nombredor(39)
1.618033988749895Valeur approchée de $\sqrt{3}$
Chez les mathématiciens grecs, extraire la racine carrée de a revient à trouver un carré dont l’aire soit a. En prenant un rectangle de côté arbitraire x et de même aire, il est nécessaire que l’autre côté ait pour longueur $\frac{a}{x}$. Pour le rendre « moins rectangle », il suffit de considérer un nouveau rectangle dont la longueur est la moyenne arithmétique des deux côtés précédents soit $\frac {x+\frac{a}{x}}{2}$ et dont l’aire reste a.
En réitérant infiniment le processus, le rectangle se transforme petit à petit en un carré de même aire. Cette constatation est à la base de la méthode de Héron.
On crée une fonction qui prend en paramètres le nombre a dont on veut calculer la racine, le nombre x, strictement positif qui est la longueur du côté du rectangle de départ et le nombre n qui est le nombre de fois où l’on réitère l’opération.
def Heron(a,x,n):
for i in range(n):
x=(x+a/x)/2
return xUtilisation :
>>> Heron(3,1,10)#On peut ainsi calculer une approximation de racine de 3
1.7320508075688772
>>> Heron(2,1,8)#On peut aussi calculer une approximation de racine de 2
1.414213562373095Toutes les approximations de $\sqrt{3}$ ainsi obtenues sont des fractions que l’on peut avoir envie de « voir » :
from fractions import *
def Heron2(a,x,n):
x= Fraction(x)
for i in range(n):
x=(x+3/x)/2
return xUtilisation :
>>> for i in range(7):
Heron2(3,1,i)
Fraction(1, 1)
Fraction(2, 1)
Fraction(7, 4)
Fraction(97, 56)
Fraction(18817, 10864)
Fraction(708158977, 408855776)
Fraction(1002978273411373057, 579069776145402304)L’algorithme de Heron est suffisamment rapide pour calculer presque instantanément des centaines de décimales de $\sqrt{3}$ :
from decimal import *
def Heron3(a,x,n):
getcontext().prec=n+1
x=Decimal(x)
for i in range(10):#Changer ce 10 pour davantage de decimales cherchées
x=(x+Decimal(a)/x)/2
return xUtilisation :
>>> Heron3(3,1,400)
Decimal('1.732050807568877293527446341505872366942805253810380628055806979451933016908800037081146186
75724857567562614141540670302996994509499895247881165551209437364852809323190230558206797482010108467
49232650153123432669033228866506722546689218379712270471316603678615880190499865373798593894676503475
06576050756618348129606100947602187190325083145829523959832997789824508288714463832917347224163984587
8553976')Vous pouvez vérifier ici.
Valeur approchée de $\ln{2}$
En écrivant $\ln(2)=\int_{1}^{2} \frac{1}{t}dt$ et en subdivisant de manière de plus en plus fine l’intervalle [1 ; 2] pour approcher cette intégrale par une somme de Riemann.
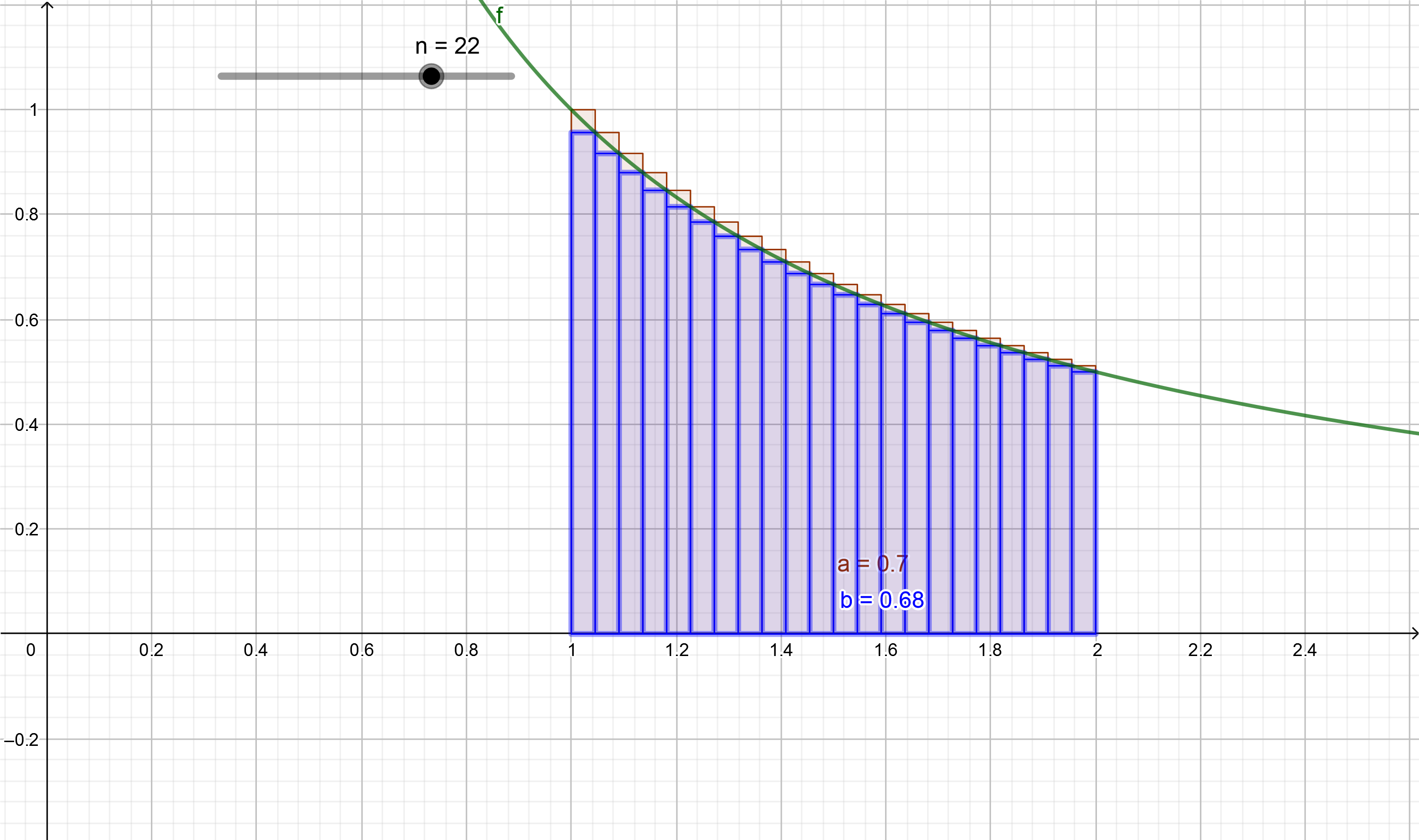
Nous verrons cela plus loin dans l’article.
Nous allons donc calculer $ln(2)$ au moyen de la série harmonique alternée : ${\displaystyle \ln(2) =\lim _{n\to \infty }\left(\sum _{k=1}^{n}{\frac {(-1)^{k + 1}}{k}}\right)}$
def ln2(n):
ln2=0
for i in range(1,n+1):
ln2+=(-1)**(i+1)/i
return ln2Utilisation :
>>> ln2(1000)
0.6926474305598223
>>> ln2(10000)
0.6930971830599583Cela converge très lentement puisque $\ln(2) \approx 0.69314718056$ ...
Valeur approchée de $\gamma$, la constante d’Euler-Mascheroni
La constante d’Euler-Mascheroni est une constante mathématique, utilisée principalement en théorie des nombres, définie comme la limite de la différence entre la série harmonique et le logarithme naturel. On la note usuellement $\gamma$.
La constante d’Euler-Mascheroni est définie par : ${\displaystyle \gamma =\lim _{n\to \infty }\left(1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\dots +{\frac {1}{n}}-\ln(n)\right)}$.
Ou encore : ${\displaystyle \gamma =\lim _{n\to \infty }\left(\sum _{k=1}^{n}{\frac {1}{k}}-\ln(n)\right)}$
La constante peut également être définie sous la forme explicite d’une série (telle qu’elle fut d’ailleurs introduite par Euler) :
${\displaystyle \gamma =\sum _{k=1}^{\infty }\left[{\frac {1}{k}}-\ln \left(1+{\frac {1}{k}}\right)\right]}$
La série harmonique diverge, tout comme la suite de terme général ${\displaystyle \ln(n)}$, l’existence de cette constante indique que les deux expressions sont asymptotiquement liées.
En utilisant cette dernière expression :
from math import log
def gamma(n):
g=0
for i in range(1,n+1):
g+=1/i-log(1+1/i)
return gUtilisation :
>>> gamma(10)
0.5310729811698833
>>> gamma(100)
0.5722570007983613
>>> gamma(1000)
0.5767160812351261
>>> gamma(1000000)
0.5772151649020281La convergence est très lente, en effet $\gamma \approx 0,577 215 664 9$, on n’a donc que 6 décimales correctes pour $n = 10^6$.
Méthode de dichotomie.
Une méthode dichotomique est une méthode algorithmique de recherche où à chaque étape on coupe l’intervalle de recherche en deux parties, le but étant de diminuer l’intervalle de recherche.
On peut appliquer la méthode dichotomique à trois types de problèmes :
La recherche d’un nombre inconnu.
On peut programmer un jeu qui consiste à trouver un nombre entre 0 et 100 choisi aléatoirement par le programme :
from random import randrange
def DevineNombre():
nb_inconnu=randrange(0,101)
nb_coups=1
nb_propose=int(input("Proposez une valeur pour le nombre inconnu : "))
while nb_inconnu!=nb_propose:
nb_coups+=1
if nb_inconnu>nb_propose:
print("Votre nombre est plus petit que le nombre inconnu.")
nb_propose=int(input("Proposez une nouvelle valeur pour le nombre inconnu : "))
else:
print("Votre nombre est plus grand que le nombre inconnu.")
nb_propose=int(input("Proposez une nouvelle valeur pour le nombre inconnu : "))
print("Gagné en ",nb_coups," coups !")Utilisation :
>>> DevineNombre()
Proposez une valeur pour le nombre inconnu : 50
Votre nombre est plus petit que le nombre inconnu.
Proposez une nouvelle valeur pour le nombre inconnu : 75
Votre nombre est plus grand que le nombre inconnu.
Proposez une nouvelle valeur pour le nombre inconnu : 62
Votre nombre est plus petit que le nombre inconnu.
Proposez une nouvelle valeur pour le nombre inconnu : 69
Votre nombre est plus grand que le nombre inconnu.
Proposez une nouvelle valeur pour le nombre inconnu : 65
Votre nombre est plus petit que le nombre inconnu.
Proposez une nouvelle valeur pour le nombre inconnu : 67
Votre nombre est plus petit que le nombre inconnu.
Proposez une nouvelle valeur pour le nombre inconnu : 68
Gagné en 7 coups !La dichotomie est ici dans la méthode de recherche du nombre, méthode que l’on peut programmer :
def RechercheAuto():
nb_inconnu=randrange(0,101)
a=0
b=100
nb_coups=1
while b>a+1:
nb_coups+=1
nb_propose=floor((a+b)/2)
if nb_propose<nb_inconnu:
a=nb_propose
else:
b=nb_propose
nb_propose=round(nb_propose)
print("La valeur inconnue est : ",nb_propose,", touvée en ",nb_coups," coups.")Résolution d’une équation du type f(x) = 0.
Soit f une fonction strictement monotone, continue et changeant de signe sur l’intervalle [a ; b], c’est-à-dire $f(a)f(b) < 0$. L’intervalle de recherche est [a ; b].
Exemples :
 |
 |
À chaque étape, on partage l’intervalle en deux en considérant le centre m de cet intervalle, ensuite suivant le signe de $f(m)$, on restreint l’intervalle de recherche à la moitié de l’intervalle précédent. Et on continue en appliquant à l’intervalle obtenu la même procédure qu’à l’intervalle précédent, et ainsi de suite …
La recherche de la solution s’arrête lorsque le centre du dernier intervalle obtenu est considéré comme étant suffisamment proche de la solution cherchée. Pour cela, on se réfère à une condition d’arrêt fixée au départ.
La précision ne porte pas sur $f(m)$ car $f(m) < \epsilon$ n’implique pas que m soit proche de $x_0$ où $f(x_0) = 0$.
def dichotomie(f,a,b,epsilon):
while b-a>epsilon:
m=(a+b)/2
if f(m)==0:
a=m
b=m
else:
if f(a)*f(m)<0:
b=m
else:
a=m
return aUtilisation
>>> def f(x):
return x**2-3*x+2
>>> dichotomie(f,1.6,2.6,0.000001)
1.9999996185302735Recherche d’un maximum.
La recherche d’un maximum pour une fonction donnée sur un intervalle [a ; b] où il y a un changement de variations et un seul .
Le principe de dichotomie se déroule de la manière suivante :
- On coupe l’intervalle de recherche en deux parties, suivant le milieu m de l’intervalle. Puis on détermine le milieu de chacun des deux intervalles formés m1 et m2.
- On calcule les valeurs atteintes par f au milieu de l’intervalle de recherche f(m), et au milieu des deux demi intervalles f(m1) et f(m2).
- Enfin, on compare f(m1) à f(m) et f(m2) à f(m) :
Si f(m1)>f(m) le maximum est dans l’intervalle [a ; m] qui a pour milieu m1 ;
Si f(m2)>f(m) le maximum est dans l’intervalle [m ; b] qui a pour milieu m2 ;
si aucun des cas précédents ne se produit, le maximum est dans l’intervalle [m1 ; m2] qui a pour milieu m. - On recommence au début et on s’arrête lorsque la longueur de l’intervalle obtenu est inférieur à la précision choisie, l’approximation du nombre où le maximum est atteint sera donné par le centre du dernier intervalle obtenu.
Pour la recherche d’un minimum, il faut juste adapter un peu l’algorithme :
Si f(m1)<f(m) le minimum est dans l’intervalle [a ; m] qui a pour milieu m1 ;
Si f(m2)<f(m) le minimum est dans l’intervalle [m ; b] qui a pour milieu m2 ;
si aucun des cas précédents ne se produit, le minimum est dans l’intervalle [m1 ; m2] qui a pour milieu m.
def extremum(f,a,b,epsilon,choix): while b-a>epsilon: m=(a+b)/2 m1=(a+m)/2 m2=(m+b)/2 if choix=="max": if f(m1)>f(m): b=m elif f(m2)>f(m): a=m else: a=m1 b=m2 elif choix=="min": if f(m1)<f(m): b=m elif f(m2)<f(m): a=m else: a=m1 b=m2 else: print("Tu dois indiquer si tu cherches un minimum ou un maximum !") break return aUtilisation :
>>> from math import sin >>> def f(x): return x**2-sin(x) >>> extremum(f,0,1,0.0000001,"min") 0.45018357038497925 >>> def f(x): return -x**2-sin(x) >>> extremum(f,-1,0,0.0000001,"max") -0.450183629989624
Méthode de Newton, méthode de la sécante
Méthode de Newton
Partant d’une abscisse $x_0$ que l’on choisit de préférence proche de la racine à trouver, on approche la fonction au premier ordre, autrement dit, on la considère asymptotiquement égale à sa tangente en ce point :
$f (x)\approx f(x_0) + f ′(x_0)(x − x_0) $ .
Partant de là, pour trouver un zéro de cette fonction d’approximation, il suffit de calculer l’intersection de la droite tangente avec l’axe des abscisses, c’est-à-dire résoudre l’équation affine :
$0 = f(x_0) + f ′(x_0)(x − x_0) $
On obtient alors un point $x_1$ qui en général a de bonnes chances d’être plus proche du vrai zéro de f que le point $x_0$ précédent. Par cette opération, on peut donc espérer améliorer l’approximation par itérations successives (voir illustration) : on approche à nouveau la fonction par sa tangente en $x_1$ pour obtenir un nouveau point $x_2$, etc.
Cette méthode requiert que la fonction possède une tangente en chacun des points de la suite que l’on construit par itération, par exemple il suffit que f soit dérivable.
Formellement, on part d’un point $x_0$ appartenant à l’ensemble de définition de la fonction et on construit par récurrence la suite :
$x_{k+1} = x_k - \frac{f(x_k)}{f’(x_k)}$
où f ’ désigne la dérivée de la fonction f. Le point $x_{k+1}$ est bien la solution de l’équation affine $f (x_k ) + f ′( x_k ) ( x − x_k ) = 0$

def Newton(f,derivee,x0,epsilon):
x=x0
while abs(f(x))>epsilon :
x=x-f(x)/derivee(x)
return xUtilisation :
>>> from math import sin
>>> from math import cos
>>> def f(x):
return x**2-sin(x)
>>> def derivee(x):
return 2*x-cos(x)
>>> Newton(f,derivee,0.5,0.0000001)
0.8767262153968663Bien que la méthode soit très efficace, certains aspects pratiques doivent être pris en compte. Avant tout, la méthode de Newton nécessite que la dérivée soit effectivement calculée. Dans les cas où la dérivée est seulement estimée en prenant la pente entre deux points de la fonction, la méthode prend le nom de méthode de la sécante.
Méthode de la sécante
En approchant la dérivée $f ’(x_k)$ par $\frac{f ( x_k ) − f ( x_{k − 1})}{ x_k − x_{k − 1}}$
def secante(f,x0,epsilon,h):
x=x0
while abs(f(x))>epsilon :
derivee=(f(x+h)-f(x))/h
x=x-f(x)/derivee
return xUtilisation :
>>> from math import sin
>>> def f(x):
return x**2-sin(x)
>>> secante(f,0.5,0.0000001,0.0001)
0.8767262155615625Algorithme de Briggs pour le calcul du logarithme.
L’Algorithme de Briggs est le suivant :
Entrée : Un réel x strictement positif
Variable : Un entier n
Tant que x est éloigné de 1 (à 0,001 près par exemple), faire
incrémenter le compteur n ;
remplacer x par sa racine carrée
#Comme le logarithme népérien d’un nombre x proche de 1 est proche de x-1,
#on prend x-1 comme valeur approchée du logarithme ; n vaut alors le nombre de fois qu’on doit doubler x-1 pour avoir le logarithme du nombre de départ.
Faire n fois :
Multiplier le logarithme par 2
Sortie : Le nombre obtenu est le logarithme népérien de x.Ce qui donne en Python, en prenant un second paramètre p pour arrêter la boucle Tant que dès que x est éloigné de 1 de moins de $10^{-p}$ :
from math import *
def ln(x,p):
n=0
while(abs(x-1)>10**(-p)):
n+=1
x=sqrt(x)
y=x-1
while(n>0):
y=y*2
n=n-1
return yUtilisation :
>>> ln(5,3)
1.6100704732402846
>>> ln(5,8)
1.609437882900238
>>> from math import log
>>> log(5)
1.6094379124341003Alors que la calculatrice donne 1.609437912 et WolframAlpha 1.609437912434100374600759333226187639525601354268517721912...
On constate que la précision pour ln(5,8) est donc d’environ $3\times 10^{-8}$
Résolution par la méthode d’Euler de $y’ = y$, et de $y’ = ay + b$.
En mathématiques, la méthode d’Euler est une procédure numérique pour résoudre par approximation des équations différentielles du premier ordre avec une condition initiale. C’est la plus simple des méthodes de résolution numérique des équations différentielles.
Pour h proche de 0, on a $y(a+h) \approx y(a) + h y’(a)$ .Nous allons utiliser cette approximation affine pour construire pas à pas une fonction vérifiant une équation différentielle du premier ordre et passant par un point donné $(x_0 ; y_0)$.
Soit l’équation différentielle définie par $y’=y$ et les conditions initiales $(x_0 ; y_0)$. En $(x_0 ; y_0)$, on connaît la pente de la tangente à partir de l’équation différentielle, $y_0$. On assimile alors sur l’intervalle $[x_0 ; x_0 + h]$ la fonction à sa tangente. On détermine alors le point $(x_1 ; y_1)$ avec $x_1 = x_0 + h$ et $y_1 = y_0 + hy_0 = y_0(1 + h)$. On recommence le même raisonnement avec le point $(x_1 ; y_1)$. On poursuit en construisant la suite de points $(x_n ; y_n)$ et en assimilant la courbe à une application affine par morceaux.
def Euler(x0,xf,y0,n):
x=x0
y=y0
h=(xf-x0)/float(n)
abscisse=[x0]
ordonnee=[y0]
for i in range(n):
x=x+h
y=y*(1+h)
abscisse.append(x)
ordonnee.append(y)
return ordonneeUtilisation :
>>> Euler(0,3,1,30)
[1, 1.1, 1.2100000000000002, 1.3310000000000004, 1.4641000000000006, 1.6105100000000008, 1.771561000000001,
1.9487171000000014, 2.1435888100000016, 2.357947691000002, 2.5937424601000023, 2.853116706110003,
3.1384283767210035, 3.4522712143931042, 3.797498335832415, 4.177248169415656, 4.594972986357222,
5.054470284992944, 5.559917313492239, 6.115909044841463, 6.72749994932561, 7.400249944258172, 8.140274938683989,
8.954302432552389, 9.849732675807628, 10.834705943388391, 11.91817653772723, 13.109994191499954,
14.420993610649951, 15.863092971714948, 17.449402268886445]Le graphique ci-dessous est réalisé avec les données ci-dessus et les valeurs exactes.

Soit l’équation différentielle définie par $y’= ay + b$ et les conditions initiales $(x_0 ; y_0)$. En $(x_0 ; y_0)$, on connaît la pente de la tangente à partir de l’équation différentielle, $ay_0 + b$. On assimile alors sur l’intervalle $[x_0 ; x_0 + h]$ la fonction à sa tangente. On détermine alors le point $(x_1 ; y_1)$ avec $x_1 = x_0 + h$ et $y_1 = y_0 + h (ay_0 + b)$. On recommence le même raisonnement avec le point $(x_1 ; y_1)$. On poursuit en construisant la suite de points $(x_n ; y_n)$ et en assimilant la courbe à une application affine par morceaux.
def Euler(x0,xf,y0,n,a,b):
x=x0
y=y0
h=(xf-x0)/float(n)
abscisse=[x0]
ordonnee=[y0]
for i in range(n):
x=x+h
y=y+h*(a*y+b)
abscisse.append(x)
ordonnee.append(y)
return ordonneeUtilisation :
>>> Euler(0,3,2,30,-0.5,0)
[2, 1.9, 1.805, 1.71475, 1.6290125, 1.547561875, 1.47018378125, 1.3966745921875001, 1.3268408625781252,
1.2604988194492188, 1.1974738784767578, 1.13760018455292, 1.080720175325274, 1.0266841665590103,
0.9753499582310597, 0.9265824603195068, 0.8802533373035314, 0.8362406704383548, 0.7944286369164371,
0.7547072050706152, 0.7169718448170844, 0.6811232525762302, 0.6470670899474187, 0.6147137354500477,
0.5839780486775453, 0.5547791462436681, 0.5270401889314846, 0.5006881794849104, 0.4756537705106649,
0.45187108198513165, 0.4292775278858751]

Et l’on peut généraliser le processus :
Soit l’équation différentielle définie par $y’=f(x,y)$ et les conditions initiales $(x_0 ; y_0)$. En $(x_0 ; y_0)$, on connaît la pente de la tangente à partir de l’équation différentielle, $f(x_0 ; y_0)$. On assimile alors sur l’intervalle $[x_0 ; x_0 + h]$ la fonction à sa tangente. On détermine alors le point $(x_1 ; y_1)$ avec $x_1 = x_0 + h$ et $y_1 = y_0 + hf(x_0,y_0)$. On recommence le même raisonnement avec le point $(x_1 ; y_1)$. On poursuit en construisant la suite de points $(x_n ; y_n)$ et en assimilant la courbe à une application affine par morceaux.
La fonction « Euler » ci-dessous prend comme dernier argument une fonction de deux variables :
def Euler(x0,xf,y0,n,f):
x=x0
y=y0
h=(xf-x0)/float(n)
abscisse=[x0]
ordonnee=[y0]
for i in range(n):
x=x+h
y=y+h*f(x,y)
abscisse.append(x)
ordonnee.append(y)
return ordonneeOn peut tester la fonction précédente avec f définie par f(x,y)=-0.5y :
>>> def f(x,y):
... return -0.5*y
...
>>> Euler(0,3,2,30,f)
[2, 1.9, 1.805, 1.71475, 1.6290125, 1.547561875, 1.47018378125, 1.3966745921875001, 1.3268408625781252,
1.2604988194492188, 1.1974738784767578, 1.13760018455292, 1.080720175325274, 1.0266841665590103,
0.9753499582310597, 0.9265824603195068, 0.8802533373035314, 0.8362406704383548, 0.7944286369164371,
0.7547072050706152, 0.7169718448170844, 0.6811232525762302, 0.6470670899474187, 0.6147137354500477,
0.5839780486775453, 0.5547791462436681, 0.5270401889314846, 0.5006881794849104, 0.4756537705106649,
0.45187108198513165, 0.4292775278858751]Ce qui donne bien le résultat précédent comme on s’y attendait.
Méthodes des rectangles, des milieux, des trapèzes.
On note $(x_i)_{i \in\{0, ..., n\}}$ une subdivision de l’intervalle [a ; b] Avec $a=x_0 < x_1 < ... < x_n = b$ et pour tout $i \in \{0, ..., n\}, x_i=a+i{\frac {b-a}{n}}$.
Il y a plusieurs méthodes pour approcher l’aire sous la courbe d’une fonction continue à l’aide de rectangles, commençons par la méthode des rectangles à gauche :
On remplace $f$ par la valeur qu’elle prend sur le bord gauche de l’intervalle $[x_i ; x_{i + 1}]$ soit $f(x_i)$, l’aire est alors égale à $f(x_i)\times{\frac{b - a}{n}}$.

D’où l’algorithme suivant :
def rectangles_gauche(f,a,b,n):
h=(b-a)/n
L=0
for i in range(n):
L+=f(a+i*h)
return h*LUtilisation :
>>> rectangles_gauche(f,1,5,30)
24.54518518518518Pour la méthode des rectangles à droite il suffit d’un tout petit changement :

def rectangles_droit(f,a,b,n):
h=(b-a)/n
A=0
for i in range(1,n+1):
A+=h*f(a+i*h)
return AUtilisation :
>>> rectangles_droit(f,1,5,30)
26.145185185185184Ces méthodes minorent ou majorent le calcul d’aire selon les variations de $f$.
Une variante de ces deux méthodes consiste à prendre comme hauteur de chaque rectangle l’image du centre de l’intervalle d’où :

def methode_milieux(f,a,b,n):
h=(b-a)/n
A=0
for i in range(n):
A+=h*f(a+(i+0.5)*h)
return AUtilisation :
>>> methode_milieux(f,1,5,30)
25.327407407407406Au lieu de remplacer $f$ par une fonction constante sur l’intervalle $[x_i ; x_{i + 1}]$, on peut la remplacer par une fonction affine représentée par le segment qui joint les points $(x_i ; f(x_{i}))$ et $(x_{i + 1} ; f(x_{i + 1}))$ :

def trapezes(f,a,b,n):
h=(b-a)/n
A=0
for i in range(n) :
A+=h*(f(a+i*h)+f(a+i*h+h))/2
return AUtilisation :
>>> trapezes(f,1,5,30)
25.345185185185183Méthode de Monte-Carlo.
Cette méthode a été abordée en classe de première mais c’était limité au cas où $0\leq x\leq 1$ et $0\leq y\leq 1$, on va étendre la méthode au cas où $a\leq x\leq b$ et $0\leq y\leq M$ où M est un majorant de $f(x)$ sur $[a ; b]$.

On va tirer au hasard N points de coordonnées comprises entre a et b pour l’abscisse et entre 0 et M pour l’ordonnée, on compte le nombre de points S sous la courbe, l’aire sous la courbe est alors approchée par S/N*(b-a)*M.
from random import *
def f(x):
return x**2-3*x+5
def monte_carlo(f,a,b,M,n):
S = 0
for k in range(n):
(x,y) = (a+(b-a)*random(),M*random())
if y < f(x):
S += 1
return S/n*M*(b-a)Utilisation :
>>> monte_carlo(f,1,5,25,1000000)
25.343799999999998Algorithme de Brouncker pour le calcul de ln(2)
On a précédemment approché $ln(2)$ avec la formule $ln(2) \approx 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \frac{1}{7} ...$ or on peut remarquer que $1 - \frac{1}{2} = \frac{1}{1\times 2}$, $\frac{1}{3} - \frac{1}{4} = \frac{1}{3\times 4}$, $\frac{1}{5} - \frac{1}{6} = \frac{1}{5\times 6}$, ... donc on peut écrire $ln(2)\approx \frac{1}{1\times 2} + \frac{1}{3\times 4} + \frac{1}{5\times 6} + + \frac{1}{7\times 8} + ...$ d’où la formule de Lord Brouncker ${\displaystyle \ln(2) =\lim_{n\to \infty} \left(\sum_{k=0}^{n}{\frac {1}{(2k+1)(2k+2)}}\right)}$ d’où l’algorithme suivant :
def brouncker(n):
ln2=0
for i in range(n):
ln2+=1/((2*i+1)*(2*i+2))
return ln2Utilisation :
>>> brouncker(20)
0.6808033817926938
>>> brouncker(200)
0.691898743055063
>>> from math import log
>>> log(2)
0.6931471805599453On peut voir que ça ne converge pas très vite même si cela est plus rapide qu’avec la série alternée.
Probabilités
Dans le cadre d’une résolution de problème modélisé par une variable binomiale X, calculer numériquement une probabilité du type P(X=k), P(X≤k), P(k≤X≤k′), en s’aidant au besoin d’un algorithme ; chercher un intervalle I pour lequel la probabilité P(X∈I) est inférieure à une valeur donnée $\alpha$, ou supérieure à $1 - \alpha$.
Soit X une variable aléatoire suivant une loi binomiale de paramètres n et p, notée $\mathscr{B}(n ; p)$.
Propriété : $P(X=k)= \binom{n}{k} p^k (1-p)^{n-k}$ avec $\binom{n}{k} = \frac{n !}{k !(n - k) !}$, d’où l’algorithme suivant :
def factorielle(n):
if n==0:
return 1
else:
return n*factorielle(n-1)
def C(n,k):
return factorielle(n)//(factorielle(k)*factorielle(n-k))
def binomFdp(n,p,k):
return C(n,k)*p**k*(1-p)**(n-k)Pour ceux qui préfèrent une version non récursive de la fonction factorielle :
def factorielle(n):
if n==0:
return 1
else:
resultat=1
for i in range(1,n+1):
resultat*=i
return resultatPropriété : $P(X\leq k)= P(X=0) + P(X=1) + ... + P(X=k) = \binom{n}{0} p^0 (1-p)^{n-0} + \binom{n}{1} p^1 (1-p)^{n-1} + ... + \binom{n}{k}p^k (1-p)^{n-k}$ , d’où l’algorithme suivant :
def binomFrep(n,p,k):
return sum(binomFdp(n,p,k) for k in range(k+1))Propriété : $P(k\leq X\leq k{’})= P(X=k) + P(X=k + 1) + ... + P(X=k{’})$,
soit $P(k\leq X\leq k{’})= \binom{n}{k} p^k (1-p)^{n-k} + \binom{n}{k+1} p^{k + 1} (1-p)^{n - k - 1} + ... + \binom{n}{k{’}} p^k{’} (1-p)^{n-k{’}}$ d’où l’algorithme suivant :
def binomFrep2(n,p,k1,k2):
return sum(binomFdp(n,p,k) for k in range(k1,k2+1))Utilisation :
>>> binomFdp(15,0.2,7)
0.013819057274880012
>>> binomFrep(15,0.2,7)
0.9957602502901768
>>> binomFrep2(15,0.2,5,7)
0.1599939742269441Si l’on veut chercher un intervalle I pour lequel la probabilité P(X∈I) est inférieure à une valeur donnée $\alpha$, on va chercher un intervalle de type $[0 ; k]$ avec $k$ le plus grand possible tel que $P(X\leq k) < \alpha$, d’où l’algorithme suivant :
def invbinom(alpha,n,p):
k = 0
S = 0
while S<alpha:
S += binomFdp(n,p,k)
k += 1
return [0,k-1]Utilisation :
>>> invbinom(0.05,100,0.3)
[0, 23]
>>> invbinom(0.15,100,0.3)
[0, 25]Si l’on veut chercher un intervalle I pour lequel la probabilité P(X∈I) est supérieure à une valeur donnée $1 - \alpha$, on va chercher un intervalle de type $[0 ; k]$ avec $k$ le plus petit possible tel que $P(X \leq k) > 1 - \alpha$, d’où l’algorithme suivant :
def invbinom_sup(alpha,n,p):
k = 0
S = 0
while S<1-alpha:
S += binomFdp(n,p,k)
k += 1
return [0,k-1]Utilisation :
>>> invbinom_sup(0.15,100,0.3)
[0, 35]Pour déterminer un intervalle de fluctuation au seuil de $100\%- \alpha$ du nombre de succès :
def intervalle_fluctuation(alpha,n,p):
a = 0
s = binomFdp(n,p,a)
while s<alpha/2:
a+=1
s+=binomFdp(n,p,a)
b = a
while s<1-alpha/2:
b+=1
s+=binomFdp(n,p,b)
return [a,b]Utilisation :
>>> intervalle_fluctuation(0.05,100,0.3)
[21, 39]Remarque
>>> binomFrep2(100,0.3,22,39)
0.9501801708754631Ce qui signifie que [22 ; 39] est un intervalle qui convient ... On peut donc améliorer le programme précédent :
def intervalle_fluctuation2(alpha,n,p):
amplitude = n
cont=True
a=0
while cont:
cont=False
Max=0
for x in range(a,n-amplitude+1):
v=binomFrep2(n,p,x,x+amplitude)
if v>Max and v>1-alpha:
Max=v
a=x
rep=[a,a+amplitude]
cont=True
amplitude=amplitude-1
return repUtilisation :
>>> intervalle_fluctuation2(0.05,100,0.3)
[22, 39]Simulation de la planche de Galton.

On considère une planche de Galton de $n$ étages. Un jeton qui tombe le long de cette planche peut être simuler par $n$ épreuves de Bernoulli dont les issues équprobables sont :
– « 0 » si jeton va à gauche
– « 1 » si le jeton va à droite
Si on repère les positions possibles du jeton par un nombre entier en partant de la droite, la positon finale du jeton correspond à la somme des valeurs des $n$ épreuves. Le script suivant permet d’effectuer cette simulation :
from random import choice
import matplotlib.pyplot as plt
def chute(n):
t=0
for k in range(n):
t=t+choice([0,1])
return t
def simule_planche(n_étages,n_lancés):
résultats=[0 for k in range(n_étages+1)]
for k in range(n_lancés):
c=chute(n_étages)
résultats[c]=résultats[c]+1
plt.bar(range(n_étages+1),s)
plt.show()Et le résultat est :

Une approche légèrement différente :
from matplotlib import pyplot
from random import random
def Galton(N,L):
positions=[]
for n in range(N):
pos=0
for l in range(L):
r=random()
if r>0.5:
pos+=1 # la bille va a droite
else:
pos-=1 # sinon a gauche
positions.append(pos)
pyplot.hist(positions,range = (-L, L), bins = 2*L, color = 'blue',edgecolor = 'grey')
pyplot.xlabel(str(N)+' billes lancées sur une planche avec '+str(L)+' lignes de clous.')
pyplot.ylabel('Effectifs')
pyplot.title('Planche de Galton')Utilisation :
>>>Galton(5000,13)

Problème de la surréservation. Étant donné une variable aléatoire binomiale X et un réel strictement positif $\alpha$, détermination du plus petit entier k tel que $P(X > k)\leq \alpha$.
Une compagnie aérienne vend des billets á des voyageurs qui se désistent avec une probabilité de 10%.
Cette compagnie aérienne fait voler des avions de 300 places.
Si on prend jusqu’à 320 réservations, le nombre de passagers se présentant à l’embarquement ne dépassera pas 300 au risque maximum de 1%.
On peut alors se poser la question différemment, sachant que la compagnie possède un avion de 300 places, combien peut-elle faire de réservations pour que le nombre de passagers ne soit pas supérieur à 300 au risque maximum de 1% ?
D’où l’algorithme suivant :
def factorielle(n):
if n==0:
return 1
else:
return n*factorielle(n-1)
def C(n,k):
return factorielle(n)//(factorielle(k)*factorielle(n-k))
def binomFdp(n,p,k):
return C(n,k)*p**k*(1-p)**(n-k)
def sur_reservation2(alpha,n,p):
P = 0
k=n
while P<alpha:
P= 1-binomFrep(k,p,n)
k += 1
return k-2Utilisation :
>>> sur_reservation(0.01,300,0.9)
320Simulation d’un échantillon d’une variable aléatoire.
Dans une population de taille N présentant une caractéristique avec une probabilité p, tirage d’un échantillon de taille n.
from random import *
def simulation(N,n,p):
population=['intéressé' for n in range(round(N*p))]+['pas intéressé' for n in range(round(N*(1-p)))]
shuffle(population)
L=sample(population,n)
return L,L.count('intéressé')/nOn utilise les commandes shuffle() et sample() du module random.
Utilisation :
>>> simulation(100000,20,0.55)
(['pas intéressé', 'intéressé', 'pas intéressé', 'pas intéressé', 'pas intéressé', 'intéressé',
'intéressé', 'intéressé', 'intéressé', 'pas intéressé', 'intéressé', 'pas intéressé',
'intéressé', 'pas intéressé', 'pas intéressé', 'pas intéressé', 'intéressé', 'pas intéressé',
'intéressé', 'pas intéressé'], 0.45)Bien sûr on ne renverra pas la liste lors de l’utilisation du programme, surtout si l’on augmente la valeur de n de manière significative.
On peut alors s’intéresser à l’intervalle de confiance :
from math import *
def IC(n,f,ndigits):
return [floor(10**ndigits*(f-1/sqrt(n)))/10**ndigits,ceil(10**ndigits*(f+1/sqrt(n)))/10**ndigits]On a arrondi par défaut la borne inférieure et par excès la borne supérieure avec les commandes floor() et ceil() du module math.
Utilisation :
>>> IC(20,simulation(100000,20,0.55),3)
[0.376, 0.824]
>>> IC(100,simulation(100000,100,0.55),3)
[0.54, 0.74]Calculer la probabilité de (| Sn − pn | > √n), où Sn est une variable aléatoire qui suit une loi binomiale ℬ(n,p). Comparer avec l’inégalité de Bienaymé-Tchebychev.
Inégalité de Bienaymé-Tchebychev : Pour tout réel strictement positif $\alpha,
P \left(\left|X- E[X]\right| \geq \alpha \right)\leq \frac {\sigma^{2}}{\alpha ^{2}}$.
Puisque ici X = Sn —> ℬ(n,p), on a E(X) = np, $\sigma(X) = \sqrt{np(1 - p)}$ ainsi l’inégalité de Bienaymé-Tchebychev devient :
$P(| S_n − pn | > \sqrt{n})\leq \frac {np(1 - p)}{n}$, soit $P(| S_n − pn | > \sqrt{n})\leq p(1 - p)$.
On réutilise une partie des fonctions utilisées précédemment pour la loi binomiale :
from math import sqrt
def factorielle(n):
if n==0:
return 1
else:
return n*factorielle(n-1)
def C(n,k):
return factorielle(n)//(factorielle(k)*factorielle(n-k))
def binomFdp(n,p,k):
return C(n,k)*p**k*(1-p)**(n-k)
def BT(n,p):
return sum(binomFdp(n,p,k) for k in range(n+1) if abs(k-n*p)>sqrt(n)),p*(1-p)On obtient :
>>> BT(50,0.3)
(0.019540328780510655, 0.21)
>>> BT(100,0.7)
(0.02138561548258103, 0.21000000000000002)Ces résultats valident l’inégalité de Bienaymé-Tchebychev et montrent qu’elle est loin d’être optimale.
Remarque : on pourrait s’étonner du résultat renvoyé pour 0.7*(1-0.7). Il s’agit d’une valeur approchée car Python représente les flottants en base 2.
Simulation d’une marche aléatoire.
On pourra visualiser cette vidéo de la série 5 minutes Lebesgue pour soi ou avec ses élèves :
On simule avec le module Turtle une marche aléatoire de n pas ayant une même probabilité d´être effectués vers l’avant ou vers l’arrière. Pour que l’on voit la progression de Turtle le pas est réglé à 20 pixels et l’on change de couleur à chaque pas. Dans graphe2, on simule p déplacements de n pas dans 360/p directions. Dans graphe3, on change d’orientation à chaque pas. Dans graphe4, on simule la marche aléatoire unidimensionnelle symétrique.
from random import *
from turtle import *
def un_saut(x):
if random()<0.5:
return x-1
else:
return x+1
def position(n):
pos=0
for i in range(n):
pos+=un_saut(0)
return pos
def graphe1(n):
colormode(255)
goto(0,0)
for i in range(n):
forward(un_saut(0)*20) #Pas de 20 pixels
color((randrange(0,256), randrange(0,256),randrange(0,256)))
def graphe2(p,n):
for i in range(p):
goto(0,0)
setheading(0)
right(180*i/p)
graphe1(n)
def graphe3(n):
reset()
goto(0,0)
for i in range(n):
forward(un_saut(0)*20)
right(90*(-1)**randrange(0,2))
def graphe4(n):
reset()
goto(0,0)
setheading(0)
for i in range(n):
setheading(45*(-1)**randrange(0,2))
forward(20)Utilisation :
>>> graphe1(20)
>>> reset()
>>> graphe2(20,20)
>>> graphe3(20)Avec graphe1 :
![]()
Avec graphe2 :

Avec graphe3 :

Avec graphe4 :

Simuler 𝑁 échantillons de taille 𝑛 d’une variable aléatoire d’espérance 𝜇 et d’écart type 𝜎. Calculer l’écart type 𝑠 de la série des moyennes des échantillons observés, à comparer à 𝜎/√𝑛. Calculer la proportion des échantillons pour lesquels l’écart entre la moyenne et 𝜇 est inférieur ou égal à 𝑘𝑠, ou à 𝑘𝜎/√𝑛, pour 𝑘=1,2,3
On peut utiliser la fonction « normalvariate » du module random qui simule la variable aléatoire demandée. Voilà un exemple de son utilisation :
>>> from random import normalvariate
>>> [normalvariate(5,2) for k in range(3)]
[2.327199304389913, 5.571419395024966, 6.132182672953084]La fonction suivante permet de simuler « N » échantillons de taille « n » d’une variable aléatoire d’espérance « mu » ; et d’écart type « sigma » :
from random import normalvariate
def simule_loi_normale(n,mu,sigma):
L=[]
for k in range(n):
L.append(normalvariate(mu, sigma))
return LVoici un exemple de résultat renvoyé :
>>> simule_loi_normale(3,10,2)
[9.0981171725224, 11.189019587002004, 9.201661392138009]Pour générer la série des moyennes on procède comme ci-dessous :
from random import normalvariate
def moyenne(L):
s=0
for k in L:
s=s+k
return s/len(L)
def simule_loi_normale(n,mu,sigma):
L=[]
for k in range(n):
L.append(normalvariate(mu, sigma))
return L
def serie_moyennes(N,n,mu,sigma):
S=[]
for k in range(N):
L=simule_loi_normale(n,mu,sigma)
S.append(moyenne(L))
return SVoici un exemple de résultat renvoyé :
>>> serie_moyennes(5,10,2,0.5)
[1.7630039322421436, 1.855006147609889, 1.9425988232954574, 2.276343383620736, 2.1096081622717935]Enfin le script suivant permet de calculer la proportion des échantillons pour lesquels l’écart entre la moyenne et 𝜇 est inférieur ou égal à 𝑘𝑠, ou à 𝑘𝜎/√𝑛, pour 𝑘=1,2,3 :
from random import normalvariate
from math import sqrt
def moyenne(L):
s=0
for k in L:
s=s+k
return s/len(L)
def ecart_type(L):
e=0
m=moyenne(L)
for v in L:
e=e+(v-m)**2
return sqrt(e/len(L))
def simule_loi_normale(n,mu,sigma):
L=[]
for k in range(n):
L.append(normalvariate(mu, sigma))
return L
def serie_moyennes(N,n,mu,sigma):
S=[]
for k in range(N):
L=simule_loi_normale(n,mu,sigma)
S.append(moyenne(L))
return S
def prop_int_ksigma(N,n,mu,sigma,k):
e=0
S=serie_moyennes(N,n,mu,sigma)
for m in S:
if abs(m-mu)<k*sigma/sqrt(n):
e=e+1
return e/N
def prop_int_ks(N,n,mu,sigma,k):
e=0
S=serie_moyennes(N,n,mu,sigma)
s=ecart_type(S)
for m in S:
if abs(m-mu)<k*s:
e=e+1
return e/NVoici un exemple de résultat renvoyé :
>>> prop_int_ksigma(10000,100,5,0.2,3)
0.9972
>>> prop_int_ks(10000,100,5,0.2,3)
0.9974On retrouve bien les résultats attendus pour un intervalle « 3-𝜎 ».
Notion de liste
La génération des listes en compréhension et en extension est mise en lien avec la notion d’ensemble. Les conditions apparaissant dans les listes définies en compréhension permettent de travailler la logique. Afin d’éviter des confusions, on se limite aux listes sans présenter d’autres types de collections.
Capacités attendues
- Générer une liste (en extension, par ajouts successifs ou en compréhension).
- Manipuler des éléments d’une liste (ajouter, supprimer...) et leurs indices.
- Parcourir une liste.
- Itérer sur les éléments d’une liste.
Une liste est une séquence modifiable. Un élément d’une liste peut être de n’importe quel type.
>>> L=[6,1,69]
>>> type(L)
<class 'list'>
>>> L[2]=1969
>>> L
[6, 1, 1969]
>>> liste=[L,7,11,67,"Marie",18.2]
>>> liste
[[6, 1, 1969], 7, 11, 67, 'Marie', 18.2]
>>> [a,b]=[0,1]
>>> a
0
>>> [a,b]
[0, 1]La liste vide :
>>> L = []
>>> L
[]Longueur d’une liste : fonction len
>>> a = [0,1,2,3]
>>> len(a)
4Le type list est itérable
On peut itérer une liste :
>>> for k in [1,2,3]:
print(k,end=" ")
1 2 3Les listes supportent les tests x in list et x not in list.
>>> solide_platon=["Tétraèdre","Hexaèdre","Octaèdre","Dodécaèdre","Icosaèdre"]
>>> "polyèdre" in solide_platon
FalseConcaténation et multiplication
On concatène avec + :
>>> a=[1,2,3]
>>> b=a+[4,5]
>>> b
[1, 2, 3, 4, 5]
>>> [0,1,2]+["Marie","Mylène"]+[67,72]
[0, 1, 2, 'Marie', 'Mylène', 67, 72]On peut utiliser la concaténation pour insérer un terme à la fin de la liste, mais on préfèrera utiliser la méthode append :
>>> L = ["Benjamin","Alain"]
>>> L.append("Yves")
>>> L
['Benjamin', 'Alain', 'Yves']On multiplie avec * :
>>> [1,2,3]*3
[1, 2, 3, 1, 2, 3, 1, 2, 3]
>>> [1,2]*3
[1, 2, 1, 2, 1, 2]
>>> 2*["Pile","Face"]
['Pile', 'Face', 'Pile', 'Face']Convertir avec la fonction list
On peut convertir n’importe quel itérable en liste :
>>> list("abcdef")
['a', 'b', 'c', 'd', 'e', 'f']
>>> list(b"abcdef")
[97, 98, 99, 100, 101, 102]
>>> list((0,1,2,3,4,5))
[0, 1, 2, 3, 4, 5]
>>> list(range(10))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> list(range(5,9))
[5, 6, 7, 8]Indexing et slicing
Les listes sont des séquences, elles sont donc indexables (les items sont repérés par un indice) et sliceables (on peut en extraire des tranches grâce à des plages d’indices). Comme d’habitude, l’indice du premier item est zéro :
>>> a=[42, 43, 45, 47]
>>> a[2]
45
>>> a[2]=12
>>> a
[42, 43, 12, 47]Indices négatifs : Python numérote le dernier item avec -1, l’avant-dernier avec -2, et ainsi de suite :
>>> a=[42, 43, 45, 47]
>>> a[-1]
47
>>> a[-2]
45Si on est obligé d’initialiser les termes dans le désordre, on commencera par créer une liste triviale.
Supposons par exemple qu’on veuille L de longueur 10, on écrira :
>>> L=[None]*10
>>> L[5]=12
>>> L
[None, None, None, None, None, 12, None, None, None, None]sans déclencher d’erreur.
Un peu de slicing :
>>> a=[0,1,2,3,4,5,6,7,8,9]
>>> a[3:7]
[3, 4, 5, 6]
>>> a[3:3]
[]
>>> a[5:]
[5, 6, 7, 8, 9]
>>> a[:5]
[0, 1, 2, 3, 4]
>>> a[-3:-1]
[7, 8]
>>> a[-5:]
[5, 6, 7, 8, 9]
>>> a[:]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]On peut faire du slicing avec un pas (positif ou négatif) :
>>> a[2:20:3]
[2, 5, 8]
>>> a[::-1]
[9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
>>> a[20:2:-2]
[9, 7, 5, 3]Remplacer une tranche par une autre
Dans une liste, on peut remplacer une tranche par une autre (il s’agit d’une mutation) :
>>> L=list(range(15))
>>> L[2:5]=5*[0]
>>> L
[0, 1, 0, 0, 0, 0, 0, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]On peut utiliser ce procédé pour changer un terme :
>>> L=list(range(15))
>>> L[3:4]=[7]
>>> L
[0, 1, 2, 7, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]On peut utiliser cette méthode pour supprimer une tranche :
>>> L[2:5]=[]
>>> L
[0, 1, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]On peut utiliser ce procédé pour supprimer un terme d’indice connu :
>>> L[3:4]=[]
>>> L
[0, 1, 5, 7, 8, 9, 10, 11, 12, 13, 14]On peut utiliser ce procédé pour insérer un élément où on veut :
>>> L[5:5]=[25]
>>> L
[0, 1, 5, 7, 8, 25, 9, 10, 11, 12, 13, 14]On peut insérer une tranche :
>>> L[5:5]=[1,1,1,1,1]
>>> L
[0, 1, 5, 7, 8, 1, 1, 1, 1, 1, 25, 9, 10, 11, 12, 13, 14]Compréhension
En mathématiques (théorie des ensembles), l’axiome de compréhension est fondamental :
Axiome : Si E est un ensemble et P une propriété exprimée dans le langage de la théorie des ensembles, alors $\left\{x \in E | P\right\}$ est un ensemble.
Il est très courant en mathématiques de définir des ensembles en compréhension. L’ensemble des nombres pairs, par exemple est l’ensemble $\left\{n \in \mathbb{Z} | n\equiv 0 [2] \right\}$.
On peut avec Python définir des listes en compréhension (on dit aussi en intension avec un s) :
>>> X=[1,5,7,12]
>>> Y=[x**2 for x in X]
>>> Y
[1, 25, 49, 144]Y est la liste des carrés des nombres appartenant à X. On peut même ajouter une condition :
>>> Y=[x**2 for x in X if x**2<30]
>>> Y
[1, 25]
>>> Y=[x**2 for x in X if x<10]
>>> Y
[1, 25, 49]On peut redéfinir X à partir de X directement :
>>> X=[1,5,7,12]
>>> X=[x**2 for x in X]
>>> X
[1, 25, 49, 144]On peut imbriquer des listes en compréhension :
>>> L = [[k for k in range(m)] for m in range(6)]
>>> L
[[], [0], [0, 1], [0, 1, 2], [0, 1, 2, 3], [0, 1, 2, 3, 4]]Fusionner
Soit L une liste de listes. On peut récupérer les items des listes de L en une seule instruction :
>>> L = [[k for k in range(m)] for m in range(1,6)]
>>> L
[[0], [0, 1], [0, 1, 2], [0, 1, 2, 3], [0, 1, 2, 3, 4]]
>>> fusion=[x for SL in L for x in SL]
>>> fusion
[0, 0, 1, 0, 1, 2, 0, 1, 2, 3, 0, 1, 2, 3, 4]On peut utiliser cette technique pour effectuer des produits de listes :
>>> valeur = [1,7,8,9,10,"Valet","Dame","Roi"]
>>> couleur = ["Coeur","Carreau","Pique","Trèfle"]
>>> jeu = [(n,c) for n in valeur for c in couleur]
>>> jeu
[(1, 'Coeur'), (1, 'Carreau'), (1, 'Pique'), (1, 'Trèfle'), (7, 'Coeur'), (7, 'Carreau'), (7, 'Pique'),
(7, 'Trèfle'), (8, 'Coeur'), (8, 'Carreau'), (8, 'Pique'), (8, 'Trèfle'), (9, 'Coeur'), (9, 'Carreau'),
(9, 'Pique'), (9, 'Trèfle'), (10, 'Coeur'), (10, 'Carreau'), (10, 'Pique'), (10, 'Trèfle'), ('Valet',
'Coeur'), ('Valet', 'Carreau'), ('Valet', 'Pique'), ('Valet', 'Trèfle'), ('Dame', 'Coeur'),
('Dame', 'Carreau'), ('Dame', 'Pique'), ('Dame', 'Trèfle'), ('Roi', 'Coeur'), ('Roi', 'Carreau'),
('Roi', 'Pique'), ('Roi', 'Trèfle')]
>>> (10,"Trèfle") in jeu
TrueTrier avec sort ou sorted (arguments reverse, key)
La fonction sorted et la méthode sort font la même chose : elles trient les items dans l’ordre croissant (par défaut). La fonction sorted prend n’importe quel itérable et retourne les items dans l’ordre, sous forme de liste :
>>> L=[7,12,3,2]
>>> sorted(L)
[2, 3, 7, 12]
>>> L
[7, 12, 3, 2]La méthode sort s’applique à une liste et modifie cette liste :
>>> L.sort()
>>> L
[2, 3, 7, 12]Les deux, sort et sorted, acceptent les arguments reverse et key. L’argument reverse permet de trier dans l’ordre décroissant :
>>> sorted([7,12,3,2],reverse=True)
[12, 7, 3, 2]L’argument key permet de choisir la fonction avec laquelle on fera le tri. Si on veut trier selon la valeur absolue, on fera :
>>> sorted([-13,15,-2,6,-6],key=abs)
[-2, 6, -6, -13, 15]Très pratique avec des données complexes :
>>> def f(t):
return t[1]
>>> L=[["Marie",21],["Mylène",17],["Fred",24],["Denis",23]]
>>> sorted(L,key=f)
[['Mylène', 17], ['Marie', 21], ['Denis', 23], ['Fred', 24]]Instruction del (mot réservé)
Pour effacer un item selon son rang, ou une plage d’items :
>>> L=[7,12,3,2]
>>> del L[2]
>>> L
[7, 12, 2]Une autre syntaxe :
>>> del(L[2])On peut utiliser del sur une plage d’indices :
>>> L=list(range(11))
>>> del L[2:5]
>>> L
[0, 1, 5, 6, 7, 8, 9, 10]
>>> L=list(range(21))
>>> L
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
>>> del L[::3]
>>> L
[1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20]Méthode index
Pour trouver l’indice d’un terme :
>>> L=[0, 1, 6, 7, 8, 9, 10, 11, 12, 5, 6, 7, 8, 9, 10]
>>> L.index(6)
2C’est l’index de la première ocurrence du terme qui est renvoyé, si l’on veut l’index de la seconde ocurrence, on peut démarrer la recherche plus loin :
>>> L.index(6,3)
10Méthode count
Pour compter les occurrences d’un item :
>>> L = [1,2,1,1,1,1,2,1,2]
>>> L.count(2)
3
>>> L.count(3)
0Méthode remove
Pour supprimer une occurrence (ne supprime que la première occurrence) :
>>> L = [1,10,56,23,897,56,1000]
>>> L.remove(56)
>>> L
[1, 10, 23, 897, 56, 1000]
>>> L.remove(100000)
Traceback (most recent call last):
File "<pyshell#165>", line 1, in <module>
L.remove(100000)
ValueError: list.remove(x): x not in listMéthode append
Pour insérer un terme à la fin :
>>> L = [1,10,56,23,897,56,1000]
>>> L.append(1945)
>>> L
[1, 10, 56, 23, 897, 56, 1000, 1945]Méthode insert
Pour insérer un terme où on veut :
>>> L.insert(3,666)
>>> L
[1, 10, 56, 666, 23, 897, 56, 1000, 1945]Méthode extend
Pour étendre une liste par concaténation :
>>> LL=[456,567]
>>> L.extend(LL)
>>> L
[1, 10, 56, 666, 23, 897, 56, 1000, 1945, 456, 567]Méthode pop
Supprime le dernier terme et le retourne :
>>> L.pop()
567
>>> L
[1, 10, 56, 666, 23, 897, 56, 1000, 1945, 456]Fonction max
Retourne le plus grand élément :
>>> max(L)
1945Fonction min
Retourne le plus petit élément :
>>> min(L)
1Méthode copy
Pour copier une liste dans une autre :
>>> LL=L.copy()
>>> LL
[1, 10, 56, 666, 23, 897, 56, 1000, 1945, 456]
>>> LL==L
True
>>> LL is L
FalseMéthode clear
Pour effacer le contenu d’une liste :
>>> L.clear()
>>> L
[]