Sous la lettre « Z » se cachent en fait des intervalles de confiance et des tests d’hypothèse.
par Alain Busser, Jean-Philippe Vanroyen
Depuis au moins la version 4.0, GeoGebra possède un « calculateur de probabilités » ; celui-ci permet de représenter graphiquement des lois de probabilités choisies dans un menu et dont les paramètres sont entrés au clavier. Mais il y a également un onglet consacré aux statistiques (utile par exemple avec le tableur pour tracer une droite de régression) :
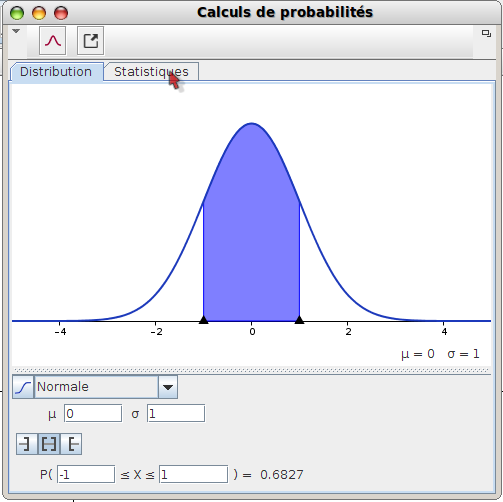
On peut alors y calculer des intervalles de confiance et y faire des tests d’hypothèse en quelques clics !
Un grand merci à Hubert Raymondeau et à Jean-Pierre Raoult dont les critiques et les suggestions ont largement contribué à donner à l’article sa forme actuelle.
Test fréquences
Monsieur James Gosling adore le café ; il achète, pour le moudre, un mélange de 100 grains de café comprenant de l’arabica, le reste étant du robusta. L’ancien vendeur puisait 30 grains dans un sac de robusta et 70 grains dans un sac d’arabica. Pour aller plus vite, le nouveau vendeur prétend avoir mélangé d’avance 700 grains d’arabica avec 300 grains de robusta, et puise dans ce mélange les 100 grains. James profite d’un séjour à Las Vegas pour demander à son ami Gil Grissom d’analyser l’échantillon qu’il a acheté : Il découvre alors que sur les 100 grains de café, il y a 40 grains de robusta, et porte plainte contre son revendeur. A-t-il raison de le faire ?
En choisissant au hasard 100 grains parmi 1000, le nombre de grains de robusta dans le mélange est inconnu d’avance, et c’est donc une variable aléatoire. Il en est donc de même pour la proportion de robusta dans le mélange (c’est le quotient du précédent par 100).
Je vous fais une petite remise ?
- Une fois qu’on a sorti le premier grain de café du sac, on ne va pas le remettre (comme au loto, on ne veut qu’une fois chaque grain). En effet, on veut avoir 100 grains de café au total (en fait on va même les prendre d’un coup avec une sorte de cuiller). Le tirage se fait donc sans remise. Dans ce cas, le nombre de grains de robusta suit une loi hypergéométrique de paramètres 1000, 300 et 100 (en admettant que le vendeur soit honnête). GeoGebra étant capable de représenter graphiquement cette loi, on vérifie graphiquement qu’avec ces paramètres, cette loi est proche d’une normale de paramètres 30 et 4,35 :
- Cependant, on peut considérer que la taille de l’échantillon (100) est suffisamment petite par rapport à celle de la population (1000) pour que le tirage soit « comme avec remise » : On considère (parce que c’est plus facile de faire des calculs avec) qu’on répète 100 fois l’expérience de tirer 1 grain de café au hasard, de regarder si c’est du robusta et de le remettre dans le sac. Dans ce cas, le nombre de grains de robusta dans l’échantillon est binomial, de paramètres 100 et 0,3 (toujours en admettant l’honnêteté du vendeur), et est approché par une normale de paramètres 30 et 4,58 :
Simulation avec tableur
Pour simuler une variable aléatoire binomiale [1] de paramètres 100 et 0,3 on peut utiliser un tableur (ça tombe bien, GeoGebra en a un), dans lequel on met =Floor(Alea()+0,3) dans 100 cellules consécutives, puis leur somme dans une 101ème cellule : Cette somme suit une variable binomiale de paramètres 100 et 0,3.
Avec le tableur de GeoGebra c’est plus facile, on peut simuler une telle variable en une seule cellule, avec =AléaBinomiale[100,0.3] :
Ce qui permet de simuler une centaine d’échantillons en une seule colonne, et de profiter du temps gagné pour faire un peu de statistiques sur ces 100 échantillons :
L’histogramme, convenablement paramétré avec le curseur, ressemble déjà à une courbe en cloche :
Pour avoir des résultats statistiques, il faut cliquer sur le bouton représentant un « Σx » (quelle logique là-dedans ?) :
La moyenne est proche de 30 et l’écart-type, de 4,9 comme il se doit :
Toutefois, une estimation ponctuelle de l’écart-type extrapolée au sac complet à partir de l’échantillon est plutôt proche de 5 (« s » au lieu de « σ »).
Ceci dit, la simulation d’une variable binomiale est plus concrète avec un langage de programmation adapté ; par exemple avec Python [2] :
Le principe du Z-test d’une proportion de GeoGebra consiste à approcher l’intervalle de fluctuation par un intervalle de fluctuation asymptotique obtenu par l’approximation normale de la fréquence empirique, et à regarder si celui-ci contient bien les 40% constatés. En fait GeoGebra va centrer et réduire la variable aléatoire en question, et la lettre Z désigne une variable aléatoire normale centrée réduite.
On choisit donc Z-test d’une proportion :
La proportion théorique est 0,3 donc l’hypothèse nulle sera p=0.3 [3]. Sur un échantillon de 100 on a 40 « succès » (grains de robusta) et la réponse du test (pour un test bilatéral, avec comme hypothèse alternative p≠0.3 comme ci-dessus) est Z=2,18 et p=0,03. Pour un test bilatéral à 5% de risque, Z doit être compris entre -1,96 et 1,96 pour accepter l’hypothèse nulle (explication des 40% par « la faute à pas de chances »). Or 2,18>1,96 donc la fluctuation d’échantillonnage ne suffit pas à expliquer à elle seule les 40% de robusta : James assigne le commerçant en justice, et celui-ci est d’ailleurs activement recherché dans les îles Kiribati où il s’est réfugié après avoir vendu son stock de robusta au prix fort...
Remarque : L’intervalle de fluctuation vu en Seconde va, dans ce cas, de 20% à 40% ; il conduit donc à une conclusion différente de celle de Terminale, à savoir que le lot est conforme...
Il suffit de cliquer sur une autre hypothèse alternative pour rendre le test unilatéral (un taux anormalement bas de robusta n’étant pas source de colère) :
On constate que la valeur de Z ne change pas par rapport au test bilatéral, seul le niveau de risque a changé. Par conséquent là encore, il y a soupçon, puisque Z>1,645 ce qui conduit à accepter l’hypothèse alternative. D’ailleurs aux Kiribati, on raconte qu’un ex vendeur de café parcourt les plages en criant « il m’a eu avec le machin du H1 ! »...
Des histoires vraies
Un Z qui veut dire « zéro »
La lettre Z désigne conventionnellement une variable aléatoire normale centrée (μ=0) et réduite (σ=1). C’est d’ailleurs celle qui s’affiche lorsqu’on ouvre le calculateur de probabilités de GeoGebra (voir l’image ci-dessus, qui ouvre l’article : on y voit que la probabilité que Z soit compris entre -1 et 1 est 0,6827 ; cette probabilité est à connaître par cœur si on en croit le programme, ainsi que les probabilités que Z soit entre -2 et 2, et entre -3 et 3).
On vérifie que la probabilité que Z soit comprise entre -1,96 et 1,96 est 0,95 :
Cette probabilité est fondamentale pour toute la suite de l’article. En tout cas pour les tests dits « bilatéraux » où le risque de 5% (1-0,95=0,05) est également réparti entre les valeurs « trop petites » (Z<-1,96) et les valeurs « trop grandes » (Z>1,96). Pour les tests « unilatéraux » où on ne s’intéresse par exemple qu’aux valeurs « trop grandes », on constate que 0,95 est aussi la probabilité que Z soit inférieur à 1,645 (graphique obtenu en cliquant sur un intervalle non borné) :
Cela est lié au fait que la probabilité de son contraire est 0,05 :
Un Z-test consiste donc à calculer la valeur de Z obtenue avec un échantillon, et à regarder si elle tombe dans la partie blanche (avec une probabilité de 0,95 si seule la fluctuation d’échantillonnage l’y a placée) ou dans la partie colorée (où on se trompe de moins de 5% en craignant que la cause soit autre que la fluctuation d’échantillonnage).
- À Woburn, sur 5969 enfants, on a compté 9 cas de leucémies, ce que les habitants ont trouvé anormalement élevé. Le test sera donc ici unilatéral (un taux anormalement bas de leucémies ne gênant personne), et voici ses résultats :
3,48 étant nettement supérieur à 1,645, le test confirme les soupçons des habitants de Woburn, mais on est (heureusement) très en-dessous du domaine de validité de l’approximation par une variable normale utilisée dans ce test.
- Rodrigo Partida a bénéficié d’une remise de peine parce que son avocat a fait valoir que sur 870 présélectionnés pour le jury qui l’a condamné, le Sherif Castaneda en a présélectionné 339 « latinos » alors que le comté à l’époque comptait 80% de latinos. Avec Z aussi petit que -30, le risque d’erreur en affirmant que la proportion de latinos est anormalement basse, est quasiment nul :
- Dans la réserve indienne d’Aamjiwnaang dans l’état d’Ontario, sur 132 naissances en un an, les indiens Chippewas ont compté seuls 46 garçons ; l’hypothèse alternative sera donc p<0.5 :
Comme -3,48 est largement en-dessous de -1,645 il y a peu de chances d’expliquer un nombre de naissances de garçons aussi bas par la fluctuation d’échantillonnage seule : En substance, lorsqu’on leur a dit « c’est la faute à pas de chance », les Chippewas ont répondu « c’est plutôt la faute à la pollution » ; et ils se trompent de moins de 5 % en disant cela [4]...
Tests de moyenne
Monsieur James (du premier onglet) boit, comme tout le monde, son café dans des tasses. Comme il a une formation scientifique, son œil a été attiré par cette publicité :
A cup of tea, or a cup of π ?
In your pickup, take a π-cup of coffee ! The content of any of our π-cups is in average, π centiliters. Sold in 6-packs, only $9.99 the 6 !
Séduit par l’idée de boire son café par doses de π centilitres, James commande un pack de 6 tasses, et avant que la garantie prenne fin, vérifie les contenances des 6 tasses ; voici en centilitres, les résultats :
| 3,2 | 3 | 2,9 | 3,1 | 3,1 | 3 |
Doit-il, oui ou non, faire jouer la garantie pour non conformité ?
Z-test bilatéral
Dans l’exemple présent, l’hypothèse dite « nulle » (μ=π peut se traduire par la nullité de μ-π) est que la contenance moyenne d’une tasse est effectivement π centilitres, et l’hypothèse « alternative » est le contraire, soit μ≠π. Il est d’usage de noter H0 et H1 ces deux hypothèses.
Si H0 est vraie, la fluctuation d’échantillonnage à elle seule explique que Z soit compris entre -1,96 et 1,96 dans 95% des échantillons. Sinon par contraposition, on estimera que H1 est plus apte que la fluctuation d’échantillonnage, à expliquer la position anormale de Z. Tout revient donc à calculer Z, qui est l’écart centré et réduit entre la valeur observée dans l’échantillon, et la valeur théorique.
Comment obtenir la moyenne et l’écart-type
Pour calculer Z, on a besoin de la moyenne théorique et de l’écart-type. Or celui-ci n’est pas donné par le constructeur [5] ; on va donc l’estimer en multipliant l’écart-type de l’échantillon par la racine de 1,2 pour réduire le biais (statistique), obtenant ainsi l’écart-type noté « s » par GeoGebra (en-dessous du « vrai » écart-type noté « σ »).
Première étape : Recopier le tableau de l’énoncé dans un tableur, ici celui de GeoGebra puisqu’on l’a sous la main, et qu’il est convivial pour les calculs statistiques :
Ci-dessus on a cliqué sur l’icône représentant un tableau et un histogramme pour faire apparaître le calculateur de statistiques, et là, on a cliqué sur l’icône représentant « Σx » pour faire apparaître les résultats statistiques, notamment n=6 et s=0,1049 dont on aura besoin plus bas.
Pour faire un Z-test sur (la conformité d’)une moyenne, on choisit l’option Z-test d’une moyenne dans le calculateur de probabilités de GeoGebra. On entre
- π comme moyenne [6] ;
- 3.05 comme moyenne de l’échantillon (copié-collé depuis le tableur) ;
- 0.1049 comme écart-type de l’échantillon ;
- et on laisse « ≠ » comme hypothèse alternative puisque c’est un test bilatéral.
On apprend alors que Z vaut environ -2,14 qui est en-dehors de l’intervalle d’acceptation de H0 (-2,14<-1,96) ; et même, la probabilité que la fluctuation d’échantillonnage seule ait donné des tasses si petites est de l’ordre de 0,03 ce qui confirme James dans ses soupçons : Il s’est fait avoir, et a renvoyé le lot de tasses au constructeur : Celui-ci aurait été aperçu dans les îles Kiribati en compagnie du marchand de café du premier onglet...
Test unilatéral
En fait, James se serait contenté de tasses trop grandes (il sait comment doser π centilitres dans une tasse de 3,5 centilitres, alors que dans une tasse de 3 centilitres, ça déborde). Alors il fait un test unilatéral, pour voir si la contenance moyenne est trop petite (et pas seulement anormale). Pour cela, il faut juste regarder si Z est, ou non, supérieur à -1,645 ; autrement dit, on clique sur une autre hypothèse alternative :
En fait la valeur de Z n’a pas bougé, et comme -2,14<-1,645 le lot est toujours non conforme (encore plus qu’avant en fait). Cette fois-ci, la probabilité que Z soit si petit est de 0,02 donc James croit encore plus qu’avant en l’hypothèse alternative.
Résumé
Pour faire un Z-test, on calcule Z puis
- pour un test bilatéral (hypothèse alternative avec un « ≠ »), on regarde si elle tombe entre -1,96 et 1,96 (auquel cas on accepte H0) ;
- pour un test unilatéral avec infériorité, on compare Z avec -1,645 et on accepte H0 si Z>-1,645
- pour l’autre test unilatéral (avec supériorité) on accepte H0 si au contraire, Z<1,645
Comparaison
Pour faire des tests de comparaison, on fait comme avec les onglets précédents mais on travaille sur la différence entre les deux quantités à comparer, en centrant puis réduisant cette différence on obtient Z :
- Si -1,96<Z<1,96 on accepte l’hypothèse nulle
- Si Z<-1,96 (Z trop petit) on accepte l’hypothèse alternative (trop petit c’est pas normal)
- Si Z>1,96 (Z trop grand) on accepte aussi l’hypothèse alternative (trop grand non plus ce n’est pas normal).
Les tests de comparaison n’étant pas vraiment au programme (un peu en BTS tout de même), seuls des tests bilatéraux seront fait ici :
Comparaison de moyennes
Extrait du sujet de BTS groupement D 1997 :
On effectue un test statistique de comparaison des moyennes de deux échantillons. Pour cela on prélève au hasard dans la population un échantillon E1 de 36 individus atteints de la maladie M et un échantillon E2 de 36 individus sains.
Pour chacun de ces individus on mesure le taux de protéines . La moyenne obtenue pour l’échantillon E1 est de 128 et la moyenne obtenue pour l’échantillon E2 est de 131.
On admet que l’écart-type du taux de protéines dans chacune des populations parentes de E1 et E1 est égal à 5,2.
Au seuil de risque 5% peut-on considérer que la maladie M modifie le taux X de ces protéines ?
On va donc faire un Z test, différence des moyennes :
Comme Z=-2,44 et que -2,44 n’est pas compris entre -1,96 et 1,96, on accepte l’hypothèse alternative : La maladie M modifie significativement le taux de protéines.
Comparaison de fréquences
Extrait du document d’accompagnement, sur les élections présidentielles françaises de 2002 :
Le 18 avril 2002, l’institut IPSOS effectue un sondage dans la population en âge de voter.
Les résultats partiels en sont les suivants :
Sur les 1000 personnes
- 135 ont déclaré vouloir voter pour Jean-Marie Le Pen
- 195 ont déclaré vouloir voter pour Jacques Chirac
- 170 ont déclaré vouloir voter pour Lionel Jospin.
Le document d’accompagnement conclut que le résultat de ce sondage ne permettait pas de conclure à un avantage de Jospin sur Le Pen, puisque les deux intervalles de confiance ont une intersection non vide. Mais un Z test, comparaison de proportions répond-il de même ?
Comme Z est nettement plus grand que 1,96 GeoGebra conclut que le score de Jospin est significativement supérieur à celui de Le Pen, ce qui est le contraire de ce qu’écrivait dans « Le Monde », le statisticien Michel Lejeune :
Pour les rares scientifiques qui savent comment sont produites les estimations, il était clair que l’écart des intentions de vote entre les candidats Le Pen et Jospin rendait tout à fait plausible le scénario qui s’est réalisé.
C’est loin d’être anecdotique : Deux algorithmes différents donnent des réponses différentes, ce qui pose sérieusement la question du choix de la méthode de test...
Intervalles de confiance
Extrait du document d’accompagnement :
On utilise un intervalle de fluctuation lorsque (...) l’on fait une hypothèse (sur la proportion p).
On utilise un intervalle de confiance lorsqu’on veut estimer une proportion inconnue dans une population.
Ce dernier cas est évoqué dans les exemples ci-dessous. En effet GeoGebra sait aussi calculer des intervalles de confiance.
Pour une moyenne
Extrait du sujet de BTS groupement D 1998 :
Pour étudier l’érythroblastose, on injecte du fer radioactif par voie veineuse, on constate que sa concentration plasmatique décroît au cours du temps ; cette décroissance est caractérisée par une période T (temps en minutes au bout duquel la concentration a diminué de moitié).
Cet examen effectué sur un échantillon de 400 sujets sains a donné les résultats suivants (en remplaçant les intervalles par leur centre) :
période 62,5 67,5 72,5 77,5 82,5 87,5 92,5 97,5 102,5 107,5 112,5 117,5 122,5 127,5 Nombre de sujets 5 11 18 29 40 51 57 54 48 35 25 15 8 4 Donner un intervalle de confiance pour la moyenne m, au seuil de risque 5%.
Calcul de la moyenne et de l’écart-type
Dans un sujet court, on aurait donné la moyenne et l’écart-type de l’échantillon, ici il faut le calculer ; mais avec un tableur sous la main c’est vite fait : On remplit la première colonne avec une suite arithmétique :
Il suffit de tirer le petit carré vers le bas :
Puis, dans « statistique à une variable », on sélectionne « données avec effectifs » [7] :
Ensuite, cliquer sur « statistiques » puis sur l’icône « Σx » :
On a alors les données qu’on peut copier-coller vers le calculateur d’intervalle de confiance (dans le calculateur de probabilités).
Pour avoir un intervalle de confiance, il faut cliquer non sur « intervalle de confiance » (on vous a bien eus hein !) mais sur « Z moyenne attendue » :
On constate qu’au lieu de la « moyenne attendue » attendue, on a bien un intervalle, et en plus décrit de deux manières :
- borne inférieure et borne supérieure comme dans le cours
- centre et rayon, un intervalle étant une boule (topologie) de dimension 1
Pour une proportionnalité
James (du premier onglet) vient de trouver une nouvelle boutique où on lui vend un « mélange secret de la maison ». Pour essayer de percer le secret, il redemande à son ami Gil (du premier onglet) d’analyser le nouvel échantillon : Surprise, là encore il y a 40 grains de robusta sur les 100.
Pour avoir un intervalle de confiance pour la proportion de robusta dans le mélange secret, il faut choisir Z estimation d’une proportion :
Le niveau de confiance est par défaut de 95% ; c’est la valeur la plus classique donc on l’a laissée.
James estime donc qu’il y a entre 30,4% et 49,6% de robusta dans le stock du commerçant ; et il se trompe de moins de 5% en affirmant cela.
Activités expérimentales
L’essentiel de ce qui est montré ci-dessous peut être fait en Seconde comme activité de découverte. C’est l’entrée algébrique de GeoGebra qui est utilisée, pas le tableur.
1) Intervalle de confiance dépendant de p
Ici p est un curseur allant de 0 à 1 ; dans ce cas si on entre
ZEstimationProportion[p,100,0.95]on obtient une liste appelée liste1 :
La borne supérieure de l’intervalle s’appelle alors Elément[liste1,2] ; on peut donc créer un point dont l’ordonnée est la différence entre cette borne supérieure et p (et d’abscisse p) :
(p,Elément[liste1,2]-p)En activant la trace de ce point, on voit que la demi-largeur de l’intervalle est pratiquement constante (et pratiquement égale à 0,1) :
On peut même écrire
(x-0.5)^2*4+y^2*100=1pour vérifier que c’est une ellipse :
En bref, on voit que pour p compris entre 0,2 et 0,8 la demi-largeur de l’intervalle est voisine de 0,1 ; alors autant fixer p à 0,5 et faire varier la taille de l’échantillon :
2) Intervalle de confiance dépendant de N
On crée un point A sur l’axe des abscisses et on entre
N=round(x(A))pour avoir la taille N de l’échantillon (un entier) ; ensuite on entre l’intervalle de confiance
ZEstimationProportion[0.5,N,0.95]puis les deux points de coordonnées
(x(A),Elément[liste1,1])
(x(A),Elément[liste1,2])En activant leur trace et en bougeant A on voit que plus N est grand, plus l’intervalle de confiance est étroit :
On peut même conjecturer les fonctions représentées graphiquement :
Pour la fonction sélectionnée ci-dessus, on a juste tapé ceci dans la barre d’entrée :
y=0.5-1/sqrt(x)3) Intervalle dépendant de la confiance
Si on a le temps (pédagogie différentiée ?) on peut refaire le tout avec d’autres niveaux de confiance que 0,95 pour voir ce que ça donne...
Cette activité qui met la charrue avant les bœufs [8], met en situation en montrant ce que sont ces intervalles de confiance avant de montrer comment on les calcule.
Et avec la Ti ?
Les candidats/cobayes du bac 2013 n’auront pas droit à GeoGebra 4.2 pour passer l’épreuve, mais ils devraient normalement avoir droit à une calculatrice graphique comme la Ti 82 Stats fr, qui elle aussi peut faire des Z-tests [9]. Dans cet onglet, à titre de comparaison, on va reprendre certains des exemples traités dans les onglets précédents, mais avec la calculatrice en question.
Intervalle de confiance pour une proportion
Aujourd’hui James (du premier onglet) a de la chance : Les tests effectués par son ami Gil sont formels : Il y a bien 30 grains de robusta dans le sachet de 100 grains qu’il a acheté à l’aéroport de Las Vegas en dutee-free. Pour estimer la proportion de robusta dans le magasin dutee-free, James sort sa Ti-82 Stats fr et calcule un intervalle de confiance :
Dans le menu stats, au lieu de edit ou calc comme on fait d’habitude, on choisit, pour une fois, le dernier menu intitulé TESTS :
1-PropZInt veut dire « one proportion Z interval » qui correspond à ce qu’on veut ici (il y a une seule proportion et Z-interval est un intervalle de confiance). On entre alors les valeurs 30 et 100, et on laisse le niveau de confiance à 0.95 (95% de confiance) ; il suffit alors d’aller sur « Calculs » :
pour avoir les bornes de l’intervalle sous la forme d’un couple :
James estime donc que le pourcentage de robusta dans le magasin est entre 21% et 39% ; la probabilité qu’il se trompe est 0,05. Il peut donc tranquillement racheter un échantillon en duty-free, les tests de Gil ayant rendu l’échantillon précédent impropre à la consommation.
Intervalle de confiance pour une moyenne
Il s’agit de l’exemple vu dans l’onglet précédent (sujet BTS groupe D 1998)
Ici il faut d’abord entrer les données pour calculer la moyenne et l’écart-type de l’échantillon. Donc on commence classiquement par « stats>edit » pour entrer les données dans L1 et les effectifs dans L2 :
Ensuite, dans le menu « stats>calc », Stats 1-Var L1, L2 permet d’avoir les statistiques nécessaires :
L’intervalle de confiance apparaît en septième entrée (« ZIntConf ») du menu « stats>Tests ». Mais cette fois-ci, au lieu de choisir « Stats » (qui nécessiterait d’entrer la moyenne et l’écart-type de l’échantillon à la main), on choisit « Val » pour avoir directement les valeurs :
Au départ, les effectifs sont tous à 1, il faut donc signaler à la calculatrice qu’ils sont dans L2, en entrant « L2 » à la place du « 1 » :
Il faut quand même entrer l’écart-type (et au passage, en profiter pour choisir S au lieu de σ) :
Ensuite, aller sur « Calculs » puis « entrée » permet d’avoir l’intervalle de confiance :
Z-test pour une moyenne
Il s’agit du même exemple que dans l’onglet 3 (tasses de contenance π centilitres) ;
Comme le test aura besoin de la moyenne et de l’écart-type de l’échantillon, on peut calculer ceux-ci avec les habituels « Stats>edit » :
puis « Stats>Calc » :
Pour faire un test d’hypothèse sur une moyenne, il faut choisir la première entrée du menu « Stats>Tests » (elle s’appelle juste « Z-Test ») :
Au lieu de « Stats » (qui nécessiterait d’entrer la moyenne et l’écart-type à la main) on choisit « Val » qui permet de récupérer les valeurs de « 1-Var Stats » ; on entre « 2nde π » pour la moyenne théorique, on recopie l’écart-type calculé tout-à-l’heure, puis on choisit l’hypothèse alternative (ici μ≠μ0) :
En allant sur « Calculs » on retrouve la valeur de Z=-2,24 vue dans le troisième onglet :
Ce qui permet de conclure comme précédemment. Sauf que à côté de l’option « calculs » qui donne le résultat, il y a une option « dessin » :
En la choisissant, on a ceci :
Et si on veut faire un test unilatéral, il suffit de changer le choix de l’hypothèse alternative :
On a toujours la même valeur de Z :
Mais le dessin rappelle que le test est unilatéral :
Z-test pour une proportion
Il s’agit de l’exemple vu dans le premier onglet (test de conformité en teneur de robusta) ;
Le test d’hypothèse portant sur une proportion s’appelle 1-PropZTest ; il suffit d’entrer 0.3 pour la proportion théorique (« p0 »), 40 et 100 pour les autres données, et de choisir « Calculs » :
Et hop, fini : On a Z=2,18 qui n’est pas inférieur à 1,645 donc le test échoue ;
et la probabilité que Z soit aussi grand est 0,015 qui est inférieur aux 5% de risque prédéfinis. On en a la confirmation visuelle en choisissant « Dessin » :
Test de comparaison de moyennes
Il s’agit du même exemple de l’onglet 4 (sujet de BTS groupement D 1997)
Le test de comparaison de moyennes est la troisième entrée du menu « Stats>Tests » ; elle s’appelle 2-CompZTest (la comparaison de fréquences étant l’entrée 6 2-PropZTest) :
Si, pour entrée, on choisit « Val », on a besoin de mettre les données dans le tableau avant toute chose :
On choisit donc « Stats » :
Ce qui change le formulaire de données à entrer.
On entre alors les nombres de l’énoncé :
Puis on choisit l’hypothèse alternative μ1≠μ2 :
Après cela, aller sur « Calculs » puis de là, appuyer sur « entrée » permet d’avoir le résultat du Z-test :
Comme Z=-2,45 qui est trop petit (inférieur à -1,96) on conclut que les moyennes sont significativement différentes au seuil de risque de 5%. D’ailleurs puisque la probabilité d’avoir une telle valeur de Z est inférieure à 0,05 (environ 0,015 d’après la calculatrice) on sait qu’on est en-dessous du risque de 5%, et on peut même conclure que les moyennes sont significativement différentes au seuil de 2%...