L’option « maths complémentaires » est la principale nouveauté dans les mathématiques mises en place avec la réforme du lycée. L’approche est thématique, les algorithmes très présents.
Cet article est long, complet et techniquement délicat : il rendra service à de très nombreux collègues.
Pourrions-nous demander aux utilisateurs de l’article de signaler les inévitables coquilles ou les anomalies qu’ils pourraient découvrir et qui nous auraient échappé...? Merci. (mathematice@sesamath.net)
Cet article peut être librement diffusé et son contenu réutilisé pour une utilisation non commerciale (contacter l’auteur pour une utilisation commerciale) suivant la licence CC-by-nc-sa
On peut lire dans le programme officiel de cette option :
Algorithmique et programmation
La démarche algorithmique est, depuis les origines, une composante essentielle de l’activité mathématique. Au collège, en mathématiques et en technologie, les élèves ont appris à écrire, mettre au point et exécuter un programme simple. Les classes de seconde et de première ont permis de consolider les acquis du collège (notion de variable, type de variables, affectation, instruction conditionnelle, boucle, notamment), d’introduire et d’utiliser la notion de fonction informatique et de liste. En algorithmique et programmation, le programme de mathématiques complémentaires reprend les programmes des classes de seconde et de première sans introduire de notion nouvelle, afin de consolider le travail des classes précédentes. Les algorithmes peuvent être écrits en langage naturel ou utiliser le langage Python. On utilise le symbole « ← » pour désigner l’affection dans un algorithme écrit en langage naturel. L’accent est mis sur la programmation modulaire qui permet de découper une tâche complexe en tâches plus simples. L’algorithmique trouve naturellement sa place dans toutes les parties du programme et aide à la compréhension et à la construction des notions mathématiques.

On va donc s’attacher à programmer les algorithmes listés dans le programme sans introduire de notions nouvelles :
Résolution d´équations du type $f(x) = k$ par balayage, par dichotomie, par la méthode de Newton.
Résolution d´équations par balayage
Cette méthode, classique, consiste, pour une fonction continue et monotone sur un intervalle $[a ; b]$ dans lequel on sait trouver la solution de $f(x) = k$, à calculer $f(x)$, pour $x$ allant de $a$ à $b$ avec un pas de $h$, après avoir vérifié la croissance ou la décroissance de la fonction. Si $f$ est croissante, « Tant Que » $f(x) < k$ est vérifiée (On utilisera pour cela un While.), on calcule $f(x)$. Dès que $f(x) > k$ on arrête l’algorithme. Si $f$est décroissante, « Tant Que » $f(x) > k$ est vérifiée, on calcule $f(x)$. Dès que $f(x) < k$ on arrête l’algorithme. On obtient un encadrement de longueur $h$ de la solution.
Il faut déterminer a et b, les bornes de l’intervalle dans lequel on va appliquer le balayage.
Fonction qui calcule cet encadrement, renvoyé dans un tuple, en fonction du nombre n de décimales souhaitées :
Cet algorithme détermine par balayage un encadrement de racine de 2 d’amplitude $10^{-n}$.
from math import cos
def f(x):
return cos(x)-x
def balayage(f,k,a,b,n):
fa,fb=f(a),f(b)
h=10**(-n)
x=a
if fa<fb:
while f(x)<k:
x=x+h
else:
while f(x)>k:
x=x+h
return (round(x-h,n),round(x,n))Utilisation : Compiler le fichier puis dans la console :
>> balayage(f,0,-1,2,6)
(0.739085, 0.739086)Le round permet ici de corriger quelques erreurs d’affichage des flottants [1].
Il est à noter que cet algorithme est très long à donner une réponse si n>=9.
On peut donc chercher à l’optimiser, par exemple en utilisant une boucle for qui va faire la même chose que le programme précédent mais pour h allant de 10-1 à 10-n en réduisant l’intervalle [a ; b] à chaque boucle.
C’est beaucoup plus rapide, jusqu’à n=16 où ça bogue, parce que les flottants (décimaux) ne sont affichés qu’avec 16 chiffres après la virgule.
def balayage2(f,k,a,b,n):
fa,fb=f(a),f(b)
for i in range(1,n+1):
h=10**(-i)
x=a
if fa<fb:
while f(x)<k:
x=x+h
else:
while f(x)>k:
x=x+h
a=x-h
return (round(x-h,n),round(x,n))Résolution d´équations par dichotomie
On va commencer par programmer l’algorithme classique de recherche de zéro d’une fonction sur un intervalle par dichotomie :
def zero(f,a,b,epsilon):
if f(a)*f(b)>0:
return "Les bornes de l'intervalle ne sont pas bien choisies."
while(abs(a-b)>epsilon):
m=(a+b)/2
if f(m)*f(a)>0:
a=m
else:
b=m
return mUtilisation :
>>> zero(f,-1,0,10**(-6))
"Les bornes de l'intervalle ne sont pas bien choisies."
>>> zero(f,-1,2,10**(-6))
0.7390849590301514Et l’on peut aisément résoudre l’équation $f(x) = k$ avec un petit aménagement :
def zero_k(f,a,b,epsilon,k):
def fk(x):
return f(x)-k
return zero(fk,a,b,epsilon)Utilisation :
>>> zero_k(f,-20,0,10**(-4),10)
-10.486984252929688Résolution d´équations du type $f(x) = k$ par la méthode de Newton.
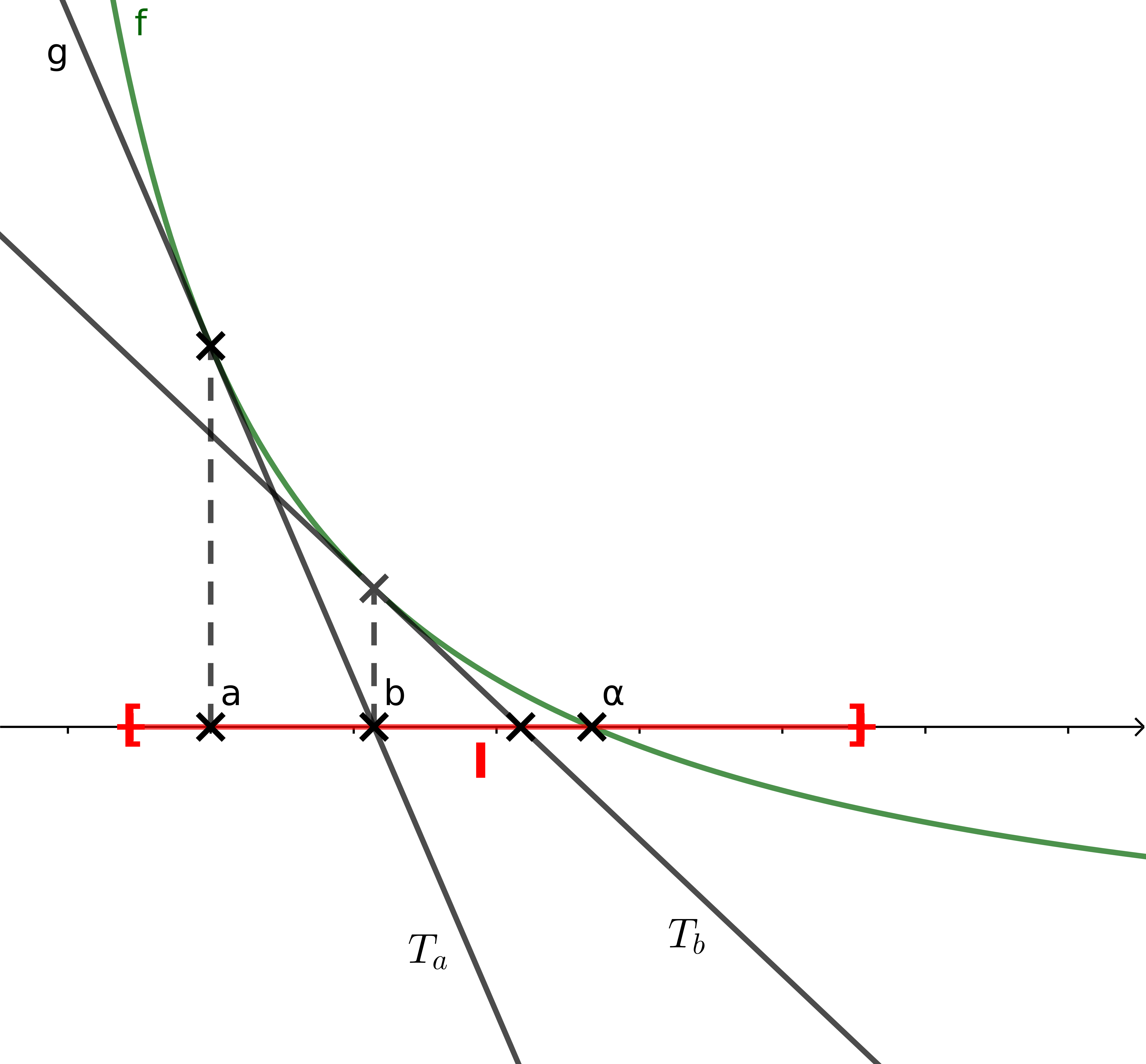
| Soit $f$ une fonction dérivable sur un intervalle $I$. L’équation $f (x) = 0$ admet une racine unique $\alpha$ sur cet intervalle $I$. Soit $a \in I$ une valeur approchée de $\alpha$. On va utiliser l’approximation affine $g$ de $f$ au point $a$. On aura donc $g(x) = f (a) + (x − a)f ′(a)$ (tangente $T_a$). La droite $T_a$ coupe l’axe des abscisses en $b = a −\frac{f(a)}{f’(a)}$. Sous certaines conditions, le nombre $b$ peut représenter une meilleure approximation de $\alpha$ que $a$. La méthode de Newton consiste à itérer le processus en repartant de $b$ et ainsi de suite. On proposera deux solutions : – si l’on sait dériver la fonction $f$.
|
Une lectrice avertie m’a fait une remarque qui m’amène à vous proposer une autre version :
def newton2(fonction,derivee,x0,e):
x = x0
while abs(fonction(x))>e:
d=derivee(x)
x = x-fonction(x)/d
return xUtilisation :
>>> newton2(f,derivee_f,2,1e-6)
0.7390851332198145
– si l’on doit se contenter d’un calcul approché de ce nombre dérivé en prenant comme approximation $f’(a) \approx \frac{f(a + h) - f(a)}{h}$ avec h suffisamment petit.
def newton3(f,x0,e,h):
x = x0
while abs(f(x))>e:
d = (f(x+h)-f(x))/h #on calcule une approximation du nombre dérivé en x
x = x-f(x)/d
return xUtilisation :
>>> newton3(f,2,1e-6,1e-5)
0.7390851332299205Recherche d’une valeur approchée de précision donnée (Dans le thème d’étude Calculs d’aires)
Méthode des rectangles, des trapèzes.
On note $(x_i)_{i \in\{0, ..., n\}}$ une subdivision de l’intervalle [a ; b] Avec $a=x_0 < x_1 < ... < x_n = b$ et pour tout $i \in \{0, ..., n\}, x_i=a+i{\frac {b-a}{n}}$.
Il y a plusieurs méthodes pour approcher l’aire sous la courbe d’une fonction continue à l’aide de rectangles, commençons par la méthode des rectangles à gauche :
On remplace $f$ par la valeur qu’elle prend sur le bord gauche de l’intervalle $[x_i ; x_{i + 1}]$ soit $f(x_i)$, l’aire est alors égale à $f(x_i)\times{\frac{b - a}{n}}$.

D’où l’algorithme suivant :
def f(x):
return x**2-3*x+5
def rectangles_gauche(f,a,b,n):
h=(b-a)/n
L=0
for i in range(n):
L+=f(a+i*h)
return L*hUtilisation :
>>> rectangles_gauche(f,1,5,30)
24.54518518518518Pour la méthode des rectangles à droite il suffit d’un tout petit changement :

def rectangles_droit(f,a,b,n):
h=(b-a)/n
L=0
for i in range(1,n+1):
L+=f(a+i*h)
return L*hUtilisation :
>>> rectangles_droit(f,1,5,30)
26.145185185185184Ces méthodes minorent ou majorent le calcul d’aire selon les variations de $f$.
Une variante de ces deux méthodes consiste à prendre comme hauteur de chaque rectangle l’image du centre de l’intervalle d’où :

def methode_milieux(f,a,b,n):
h=(b-a)/n
L=0
for i in range(n):
L+=f(a+(i+0.5)*h)
return L*hUtilisation :
>>> methode_milieux(f,1,5,30)
25.327407407407406Au lieu de remplacer $f$ par une fonction constante sur l’intervalle $[x_i ; x_{i + 1}]$, on peut la remplacer par une fonction affine représentée par le segment qui joint les points $(x_i ; f(x_{i}))$ et $(x_{i + 1} ; f(x_{i + 1}))$ :

def trapezes(f,a,b,n):
h=(b-a)/n
L=0
for i in range(n) :
L+=(f(a+i*h)+f(a+i*h+h))/2
return L*hUtilisation :
>>> trapezes(f,1,5,30)
25.345185185185183Méthode de Monte-Carlo pour un calcul d’aire.
Cette méthode a été abordée en classe de première mais c’était limité au cas où $0\leq x\leq 1$ et $0\leq y\leq 1$, on va étendre la méthode au cas où $a\leq x\leq b$ et $0\leq y\leq M$ où M est un majorant de $f(x)$ sur $[a ; b]$.

On va tirer au hasard N points de coordonnées comprises entre a et b pour l’abscisse et entre 0 et M pour l’ordonnée, on compte le nombre de points S sous la courbe, l’aire sous la courbe est alors approchée par S/N*(b-a)*M.
from random import *
def f(x):
return x**2-3*x+5
def monte_carlo(f,a,b,M,n):
S = 0
for k in range(n):
(x,y) = (uniform(a,b),uniform(0,M))
if y < f(x):
S += 1
return S/n*M*(b-a)Utilisation :
>>> monte_carlo(f,1,5,25,1000000)
25.343799999999998Chacune des méthodes précédentes peut être programmée en retournant directement la somme des éléments d’une liste plutôt que d’utiliser une boucle :
def rectangles_gauche2(f,a,b,n):
h=(b-a)/n
return sum([f(a+i*h) for i in range(n)])*h
def rectangles_droit2(f,a,b,n):
h=(b-a)/n
return sum([f(a+i*h) for i in range(1,n+1)])*h
def methode_milieux2(f,a,b,n):
h=(b-a)/n
return sum([f(a+(i+0.5)*h) for i in range(n)])*h
def trapezes2(f,a,b,n):
h=(b-a)/n
return sum([(f(a+i*h)+f(a+i*h+h))/2 for i in range(n)])*h
def monte_carlo2(f, a, b, n):
return sum([f(uniform(a, b)) for i in range(n)])*(b-a)/nPour cette dernière fonction, il n’a pas été possible de traduire la fonction monte_carlo() précédente à l’aide d’une liste, on a précédemment calculé une approximation de l’aire en procédant de la manière suivante :
– On a enfermé l’aire à calculer dans un rectangle de dimensions $(b - a)\times M$ ;
– On a lancé aléatoirement un grand nombre de points dans ce rectangle ;
– On a compté à chaque lancer ceux qui étaient sous la courbe, c’est-à-dire dans la surface que l’on veut calculer.
– On en a déduit par proportionnalité à une approximation de l’aire.
On ne peut pas simuler cela avec une liste mais on peut utiliser une variante de la méthode de Monte-Carlo (L’algorithme de la moyenne ou l’algorithme de l’espérance ou encore ici) :
– On tire aléatoirement et uniformément un grand nombre de nombres aléatoires x entre a et b ;
– On prend, à chaque tirage, comme approximation de l’aire, l’aire du rectangle de largeur b - a et de hauteur f(x) ;
– On calcule la moyenne des aires obtenues.
Il s’agit de l’algorithme monte_carlo2() ci-dessus.
Calcul des termes d’une suite - Pour une suite récurrente Un+1=f(Un), calcul des termes successifs - Calcul d’un terme de rang donné d’une suite
Les listes en compréhension sont des objets qui permettent de générer assez simplement des suites de nombres (voir Notion de liste en dernier paragraphe de cet article) :
>>> [7*i for i in range(1,11)]
[7, 14, 21, 28, 35, 42, 49, 56, 63, 70]
>>> [2*i for i in range(20)]
[0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38]
>>> [i**2 for i in range(16)]
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225]
>>> [i for i in range(100) if i%7==2]
[2, 9, 16, 23, 30, 37, 44, 51, 58, 65, 72, 79, 86, 93]Voyons maintenant, plus classiquement, le calcul de termes d’une suite définie de manière explicite, c’est-à-dire à l’aide d’une fonction de n.
def u(n):
return 3*n+1
def suite_explicite(u,debut,fin):
suite = []
for i in range(debut,fin+1):
suite.append(u(i))
return suiteAprès avoir défini la fonction u, on crée une liste vide appelée « suite » dans laquelle on ajoute (append) à l’aide d’une boucle les termes d’indice compris entre début et fin.
Si l’on veut simplement un terme de rang donné, il suffit d’utiliser la fonction u :
>>> suite_explicite(u,0,10)
[1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31]
>>> u(5)
16Une autre version avec une liste :
def suite_explicite2(u,debut,fin):
return [u(i) for i in range(debut,fin+1)]Regardons maintenant du côté des suites définies par récurrence :
def f(u_n):
return 3*u_n+1
def suite_recurrente(f,debut,fin,u_0):
suite = [u_0]
for i in range(debut,fin):
suite.append(f(suite[i-debut]))
return suiteAprès avoir défini la fonction f, qui calcule $u_{n+1}$ en fonction de $u_{n}$, on crée une liste appelée « suite » qui contient uniquement le premier terme de la liste, dans laquelle on ajoute (append) à l’aide d’une boucle les termes d’indice compris entre début+1 et fin.
>>> suite_recurrente(f,0,10,0)
[0, 1, 4, 13, 40, 121, 364, 1093, 3280, 9841, 29524]
>>> suite_recurrente(f,5,10,12)
[12, 37, 112, 337, 1012, 3037]Utilisation :
>>> suite_recurrente(f,0,10,0)
29524
>>> suite_recurrente(f,5,10,12)
3037Si l’on veut simplement un terme de rang « fin », il suffit de renvoyer suite[fin-debut] à la place de suite.
def suite_recurrente(f,debut,fin,u_0):
suite = [u_0]
for i in range(debut,fin):
suite.append(f(suite[i-debut]))
return suite[fin-debut]Utilisation :
>>> suite_recurrente(f,5,10,12)
3037
>>> suite_recurrente(f,0,10,0)
29524Recherche de seuils
Un algorithme « de seuil » permet de déterminer une valeur pour laquelle une condition est respectée pour la première fois.
Ce type d’algorithme peut être utilisé pour répondre, par exemple, à ce genre de question : « déterminer la plus petite valeur de n pour laquelle $u_n>1000$ ».
Concrètement, on considère une suite $(u_n)$ et on cherche à écrire un algorithme « de seuil » sur cette suite.
Le modèle à utiliser est le suivant (où les termes de la suite sont représentés par la lettre U et les rangs par la lettre N) :
N ← valeur initiale (souvent 0 ou 1)
U ← valeur initiale
TANT QUE condition
N ← N+1
U ← .... (le terme suivant qui dépend de l'exercice)
FIN TANT QUEOn en profite pour calculer la somme des termes de la suite entre les indices debut et fin.
Si la suite est définie de manière explicite :
def u(n):
return 3*n+1
def seuil_explicite(n_0,N):
n=n_0
while u(n)<N:
n=n+1
return n
def somme_explicite(debut,fin):
s=0
for i in range(debut,fin+1):
s=s+u(i)
return sUtilisation :
>>> seuil_explicite(5,1000)
333
>>> somme_explicite(5,9)
110Si la suite est définie de manière récurrente :
def f(u_n):
return 3*u_n+1
def seuil_recurrent(n_0,u_0,N):
n=n_0
U=u_0
while U<N:
n=n+1
U=f(U)
return n
def somme_recurrente(debut,fin,u_0):
s=u_0
u=u_0
for i in range(debut,fin):
u=f(u)
s=s+u
return sUtilisation :
>>> seuil_recurrent(5,1000,15000)
8
>>> somme_recurrente(3,7,5)
663On pourra facilement adapter ces scripts de seuil si la suite est décroissante et qu’il s’agit de déterminer à partir de quand son terme devient inférieur à une valeur donnée.
Recherche de valeurs approchées de constantes mathématiques, par exemple π, ln2,√2
Valeur approchée de π
Nous avons déjà approximé π en classe de première avec la méthode d’Archimède et la méthode de Monte Carlo, nous utiliserons en Terminale la formule de Bellard :
$\displaystyle \pi ={\frac {1}{2^{6}}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2^{10n}}}\left(-{\frac {2^{5}}{4n+1}}-{\frac {1}{4n+3}}+{\frac {2^{8}}{10n+1}}-{\frac {2^{6}}{10n+3}}-{\frac {2^{2}}{10n+5}}-{\frac {2^{2}}{10n+7}}+{\frac {1}{10n+9}}\right)$
def bellard(n):
pi=0
for i in range(n+1):
pi+=(-2**5/(4*i+1)-1/(4*i+3)+2**8/(10*i+1)-2**6/(10*i+3)-2**2/(10*i+5)-2**2/(10*i+7)+1/(10*i+9)) *(-1)**i/(2**6*2**(10*i))
return piUtilisation :
>>> bellard(3)
3.1415926535897545
>>> bellard(4)
3.1415926535897922A noter que Python ne peut faire mieux que bellard(4) qui n’est pas une bonne approximation puisque les 3 dernières décimales sont erronées. En utilisant le module Decimal, on obtient deux décimales exactes de plus, pas plus ...
Valeur approchée de $\ln{2}$
En écrivant $\ln(2)=\int_{1}^{2} \frac{1}{t}dt$ et en subdivisant de manière de plus en plus fine l’intervalle [1 ; 2] pour approcher cette intégrale par une somme de Riemann.
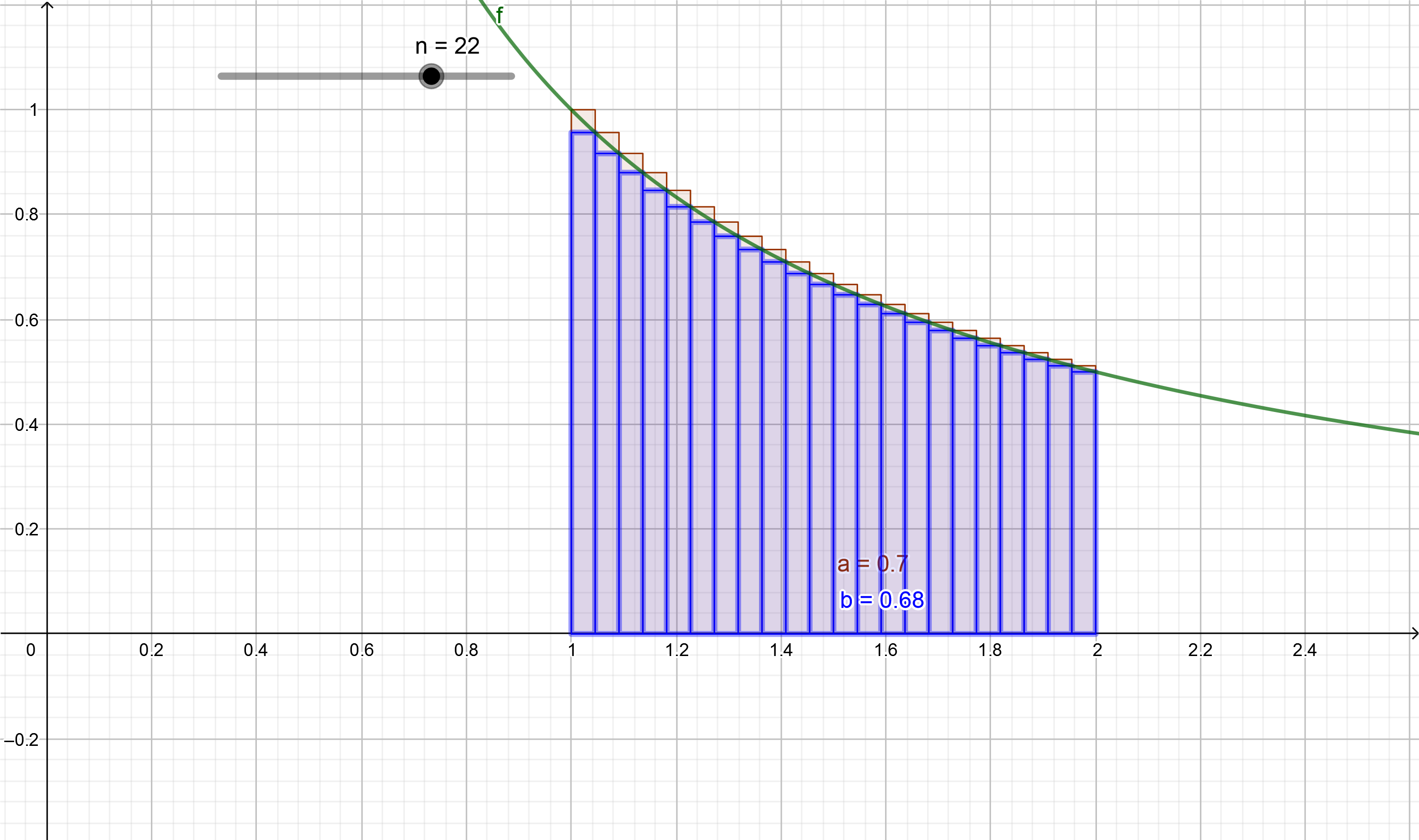
Nous verrons cela plus loin dans l’article.
Nous allons donc calculer $ln(2)$ au moyen de la série harmonique alternée : ${\displaystyle \ln(2) =\lim _{n\to \infty }\left(\sum _{k=1}^{n}{\frac {(-1)^{k + 1}}{k}}\right)}$
def ln2(n):
ln2=0
for i in range(1,n+1):
ln2+=(-1)**(i+1)/i
return ln2Utilisation :
>>> ln2(1000)
0.6926474305598223
>>> ln2(10000)
0.6930971830599583Cela converge très lentement puisque $\ln(2) \approx 0.69314718056$ ...
Valeur approchée de $\sqrt{2}$
On doit à Théon de Smyrne ces deux suites $(p_n)$ et $(q_n)$ définies par récurrence :
$p_{n + 1} = p_n + 2q_n, p_0 = 1$ ;
$q_{n + 1} = p_n + q_n, q_0 = 1$.
Ces suites sont à valeur entière strictement positive, donc strictement croissantes par récurrence, et vérifient :
$p_n² − 2q_n² = (−1)^n(p_0² − 2q_0²)$ de sorte que $\frac{p_n}{q_n}$ tend vers $\sqrt{2}$.
def racine2(n):
p,q=1,1
for i in range(n):
p,q=p+2*q,p+q
return p/qUtilisation :
>>> racine2(10)
1.4142135516460548
>>> racine2(100)
1.4142135623730951Méthode d’Euler
Soit $f$ une fonction dérivable sur $]0 ; +\infty[$ et vérifiant $f(1) = 0$ et pour tout $x \in ]0 ; +\infty[, f’(x) = \frac{1}{x}$. Utilisons la méthode d’Euler pour tracer une courbe approchée sur l’intervalle [1 ; 3] de cette fonction f.
La méthode d’Euler consiste à construire une suite de points $(x_n ; y_n)$ telle que $y_n$ soit proche de $f(x_n)$. Ainsi le nuage de points $(x_n ; y_n)$ formera une approximation de la courbe représentative de la fonction $f$.
La suite $(x_n)$ est une suite arithmétique de raison $h>0$ et de premier terme 1, $h$ est appelé le pas. On a donc $x_n = 1 + nh$ et $x_{n+1}=x_n + h$.
La suite $(y_n)$ est définie par $y_0 = f(x_0) = f(1) = 0$ et pour tout $n \in \mathbf{N}, y_{n+1}=y_n+hf’(x_n)$. C’est-à-dire que l’on se sert de l’approximation affine de la fonction par ses tangentes successives.
On a $y_{n+1}=y_n+\frac{h}{x_n}$.
D’où le script suivant :
import matplotlib.pyplot as plt
def Euler(x_f,n) :
x=1
y=0
h=x_f/n
abscisse=[1]
ordonnee=[0]
for i in range(n) :
y=y+h/x
x=x+h
abscisse.append(x)
ordonnee.append(y)
plt.plot(abscisse,ordonnee,"r")
plt.show()Utilisation, pour un nuage de n=100 points pour x allant de 1 à x_f=3 :
>>> Euler(3,100)Ce qui donne le graphique suivant :

Et si l’on veut comparer avec le « vrai » graphe de la fonction logarithme neperien :
import matplotlib.pyplot as plt
from math import log
def Euler(x_f,n) :
x=1
y=0
h=x_f/n
abscisse=[1]
ordonnee=[0]
ln=[0]
for i in range(n) :
y=y+h/x
x=x+h
abscisse.append(x)
ordonnee.append(y)
ln.append(ln(x))
plt.plot(abscisse,ordonnee,"r")
plt.plot(abscisse,ln,"b")
plt.show()

Algorithme de Briggs pour le calcul de logarithmes
L’Algorithme de Briggs est basé sur le fait que $\ln(\sqrt{x}) = \frac 1 2 \ln(x)$ (Voir page 50 de ce document du site exo7 et l’article d’Alain Busser).
Entrée : Un réel x strictement positif
Variable : Un entier n
Tant que x est éloigné de 1 (à 0,001 près par exemple), faire
incrémenter le compteur n ;
remplacer x par sa racine carrée
#Comme le logarithme népérien d’un nombre x proche de 1 est proche de x-1,
#on prend x-1 comme valeur approchée du logarithme ; n vaut alors le nombre de fois qu’on doit doubler x-1 pour avoir le logarithme du nombre de départ.
Faire n fois :
Multiplier le logarithme par 2
Sortie : Le nombre obtenu est le logarithme népérien de x.Ce qui donne en Python, en prenant un second paramètre p pour arrêter la boucle Tant que dès que x est éloigné de 1 de moins de $10^{-p}$ :
from math import *
def ln(x,p):
n=0
while(abs(x-1)>10**(-p)):
n+=1
x=sqrt(x)
y=x-1
while(n>0):
y=y*2
n=n-1
return yUtilisation :
>>> ln(5,3)
1.6100704732402846
>>> ln(5,8)
1.609437882900238
>>> from math import log
>>> log(5)
1.6094379124341003Alors que la calculatrice donne 1.609437912 et WolframAlpha 1.609437912434100374600759333226187639525601354268517721912...
On constate que la précision pour ln(5,8) est donc d’environ $3\times 10^{-8}$
Approximation de ln 2 par dichotomie selon l’algorithme de Brouncker
On a précédemment approché $ln(2)$ avec la formule $ln(2) \approx 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + \frac{1}{7} ...$ or on peut remarquer que $1 - \frac{1}{2} = \frac{1}{1\times 2}$, $\frac{1}{3} - \frac{1}{4} = \frac{1}{3\times 4}$, $\frac{1}{5} - \frac{1}{6} = \frac{1}{5\times 6}$, ... donc on peut écrire $ln(2)\approx \frac{1}{1\times 2} + \frac{1}{3\times 4} + \frac{1}{5\times 6} + + \frac{1}{7\times 8} + ...$ d’où la formule de Lord Brouncker ${\displaystyle \ln(2) =\lim_{n\to \infty} \left(\sum_{k=0}^{n}{\frac {1}{(2k+1)(2k+2)}}\right)}$ d’où l’algorithme suivant :
def brouncker(n):
ln2=0
for i in range(n):
ln2+=1/((2*i+1)*(2*i+2))
return ln2Utilisation :
>>> brouncker(20)
0.6808033817926938
>>> brouncker(200)
0.691898743055063
>>> from math import log
>>> log(2)
0.6931471805599453On peut voir que ça ne converge pas très vite même si cela est plus rapide qu’avec la série alternée.
Dans le cadre de la loi binomiale : calcul de coefficients binomiaux (triangle de Pascal), de probabilités ; détermination d’un intervalle I pour lequel la probabilité P(X∈I) est inférieure à une valeur donnée $\alpha$, ou supérieure à $1 - \alpha$.
Calcul de coefficients binomiaux (triangle de Pascal)
Le triangle de Pascal :
| 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 |
$\begin{pmatrix}0\\0\end{pmatrix}$ $\begin{pmatrix}1\\0\end{pmatrix} \begin{pmatrix}1\\1\end{pmatrix}$ $\begin{pmatrix}2\\0\end{pmatrix}\begin{pmatrix}2\\1\end{pmatrix}\begin{pmatrix}2\\2\end{pmatrix}$ $\begin{pmatrix}3\\0\end{pmatrix}\begin{pmatrix}3\\1\end{pmatrix}\begin{pmatrix}3\\2\end{pmatrix}\begin{pmatrix}3\\3\end{pmatrix}$ $\begin{pmatrix}4\\0\end{pmatrix}\begin{pmatrix}4\\1\end{pmatrix}\begin{pmatrix}4\\2\end{pmatrix}\begin{pmatrix}4\\3\end{pmatrix}\begin{pmatrix}4\\4\end{pmatrix}$ $\begin{pmatrix}5\\0\end{pmatrix}\begin{pmatrix}5\\1\end{pmatrix}\begin{pmatrix}5\\2\end{pmatrix}\begin{pmatrix}5\\3\end{pmatrix}\begin{pmatrix}5\\4\end{pmatrix}\begin{pmatrix}5\\5\end{pmatrix}$ |
La construction du triangle suit la relation de Pascal :
$\begin{pmatrix}n\\k\end{pmatrix} = \begin{pmatrix}n - 1 \\k - 1 \end{pmatrix} + \begin{pmatrix}n - 1\\k\end{pmatrix}$
Python possède une commande binomial du module Sympy (Installation du module Sympy en installant Anaconda) qui permet de calculer le coefficient binomial de deux entiers naturels :
>>> from sympy import binomial
>>> binomial(6,2)
15La commande comb() class="python" a récemment intégré le module math, on peut donc également utiliser :
>>> from math import comb
>>> comb(10,2)
45Nous allons bien sûr nous passer de cela et programmer une fonction qui calcule $\begin{pmatrix}n\\k\end{pmatrix}$ par itération.
Au lieu de construire le triangle de Pascal en entier, nous pouvons nous focaliser sur la construction de la k-ième colonne en constatant que :
$\begin{pmatrix}n\\k + 1\end{pmatrix} =\frac{{n} !}{{(k + 1) !}{(n - (k + 1)) !}} = \frac{n !}{k ! (n - k) !}\frac{n - k}{k + 1} = \frac{n - k}{k + 1}\begin{pmatrix}n\\k\end{pmatrix} $
On peut donc générer les termes en itérant à partir de $\begin{pmatrix}1\\0\end{pmatrix}$
def pascal(n,k):
coeff = 1
for i in range(k):
coeff = (coeff*(n-i))//(i+1)
return coeffUtilisation :
>>> pascal(6,2)
15
>>> pascal(10,2)
45Enfin si on utilise la commande factorial() du module math :
from math import factorial
def C(n,k):
return factorial(n)//(factorial(k)*factorial(n-k))Utilisation :
>>> C(10,2)
45
>>> C(6,2)
15On peut également programmer une fonction récursive basée sur la formule :
C(n,p)=C(n−1,p−1)+C(n−1,p)
def binomial(n,p):
if n==p or p==0:
return 1
else:
return binomial(n-1,p-1)+binomial(n-1,p)Mais cette fonction ne permet pas un calcul efficace d’un coefficient binomial un peu grand, en sorte que le calcul de binomial(30,15) peut nécessiter plusieurs minutes.
On peut faire mieux avec la formule :
$C(n,p) = C(n-1 , p-1)\times \frac{n}{p}$.
def binomial(n, p):
if n==p or p==0:
return 1
else:
return binomial(n-1,p-1)*n//pIl n’est pas très difficile d’émuler récursivement la génération ligne par ligne du tableau de Pascal et obtenir ainsi chaque coefficient binomial.
Il est pas nécessaire de créer la totalité du tableau, une liste suffit. En effet, si on dispose d’une liste comme L=[1, 4, 6, 4, 1] on peut construire la liste LL commençant par 1 suivi des sommes des termes voisins de L, dans notre cas LL=[1, 5, 10, 10, 5, 1] et ce procédé permet ainsi de générer une ligne du tableau de Pascal connaissant la précédente. On peut donc par la suite utiliser une fonction récursive :
def ligne_suivante(L):
LL=[1]
for i in range(len(L)-1):
LL.append(L[i]+L[i+1])
LL.append(1)
return LL
def ligne(n):
if n==0:
return [1]
else:
return ligne_suivante(ligne(n-1))
def pascal(n, p):
return ligne(n)[p]Utilisation :
>>> for i in range(11):
ligne(i)
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
[1, 5, 10, 10, 5, 1]
[1, 6, 15, 20, 15, 6, 1]
[1, 7, 21, 35, 35, 21, 7, 1]
[1, 8, 28, 56, 70, 56, 28, 8, 1]
[1, 9, 36, 84, 126, 126, 84, 36, 9, 1]
[1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1]
>>> pascal(10,2)
45Simulation avec Python d’une variable aléatoire (de la loi de Bernoulli, d’une loi uniforme discrète, etc.) d’un échantillon de taille 𝑛 d’une variable aléatoire.
Loi de Bernoulli
La distribution de Bernoulli ou loi de Bernoulli, du nom du mathématicien suisse Jacques Bernoulli, est une distribution discrète de probabilité, qui prend la valeur 1 avec la probabilité p et 0 avec la probabilité q = 1 – p. D’où la fonction suivante :
from random import random
def epreuve(p):
if random()<=p:
return True
else:
return FalseUn schéma de Bernoulli consiste à effectuer un certain de nombre de fois une même épreuve de Bernoulli, le résultat de chaque épreuve de Bernoulli étant indépendant des résultats des autres épreuves de Bernoulli. Le nombre d’épreuves est traditionnellement noté n :
def schema(n,p):
nb_succes=0
for i in range(n):
if epreuve(p)==True:
nb_succes+=1
return nb_succesOn considère alors X la variable aléatoire qui associe à une réalisation d’un schéma de Bernoulli le nombre de succès en n tentatives. On dit que la variable aléatoire X est régie par une loi binomiale de paramètres n et p. On note B(n,p) la loi binomiale de paramètres n et p. On peut alors réaliser une expérience qui consiste à répéter N fois le schéma de Bernoulli :
def experience(N,n,p):
frequences=[]
for i in range(N):
frequences.append(0)
for i in range(N):
nb_succes=schema(n,p)
frequences[i]=nb_succes/n
return frequencesUtilisation :
>>> experience(10,1000,0.36)
[0.354, 0.346, 0.329, 0.329, 0.39, 0.367, 0.368, 0.341, 0.352, 0.327]Loi uniforme discrète
Pour une variable aléatoire X qui suit une loi discrète uniforme sur $\{1,2,...,k\}$, on va partitionner l’intervalle [0,1] dans lequel une variable aléatoire U qui suit une loi uniforme prend ses valeurs en k sous-intervalles de taille $\frac 1 k$. Il faut ensuite déterminer dans lequel de ces sous-intervalles se trouve U. Une manière de faire cela est d’utiliser la partie entière supérieure :
from random import random
from math import ceil
def uniforme_discrete(k):
U=random()
X=ceil(k*U)
return XUtilisation :
>>> for i in range(100):
uniforme_discrete(10)
9
3
3
1
10
7
1
5
8
6Et si l’on veut un échantillon de taille n :
def schema(n,k):
L=[]
for i in range(k):
L.append(0)
for i in range(n):
sortie=uniforme_discrete(k)
for j in range(k):
if sortie==j+1:
L[j]+=1
return LUtilisation :
>>> schema(100,10)
[14, 14, 11, 5, 10, 8, 13, 9, 10, 6]
>>> schema(1000,12)
[81, 74, 80, 92, 82, 74, 91, 91, 78, 96, 77, 84]Et si l’on veut réaliser l’expérience N fois :
def experience(N,n,k):
frequences=[]
for i in range(k):
frequences.append(0)
for i in range(k):
nb_succes=schema(n,k)
frequences[i]=nb_succes[i]/n
return frequencesUtilisation :
>>> experience(10,1000,8)
[0.12, 0.124, 0.124, 0.153, 0.136, 0.141, 0.13, 0.124]
>>> experience(10,100000,8)
[0.12371, 0.12461, 0.12588, 0.12389, 0.12671, 0.1243, 0.12541, 0.12683]Loi discrète
Par exemple : Loi sur $\{-10,3,50\}$ de loi $P(-10) =\frac 2 3, P(3) =\frac 1 6, P(50) =\frac 1 6$. On partitionne l’intervalle [0,1] en trois sous-intervalles de taille respective $\frac 2 3, \frac 1 6 et \frac 1 6$. Une manière de faire consiste à prendre $[0 ; \frac 2 3], [\frac 2 3 ; \frac 2 3 + \frac 1 6], [\frac 2 3 + \frac 1 6 ; 1]$. L’algorithme est alors :
from random import random
def loi_discrete():
U=random()
if U<2/3:
X=-10
elif U<5/6:
X= 3
else:
X= 50
return XEt pour simuler n expériences :
def simule(n):
L=[0,0,0]
for i in range(n):
sortie=loi_discrete()
if sortie==-10:
L[0]+=1
elif sortie==3:
L[1]+=1
else:
L[2]+=1
return LUtilisation :
>>> simule(10000)
[6650, 1708, 1642]Et si l’on préfère récupérer les fréquences :
for i in range(3):
L[i]/=n
>>> simule(10000)
[0.6628, 0.1644, 0.1728]Avec la commande choices() du module random :
Avec les poids cumulatifs :
Pour simuler la loi discrète :
>>> from random import *
>>> choices([-10,3,50],cum_weights=[2/3,5/6,1],k=1)
[3]Et pour simuler k expériences :
>>> choices([-10,3,50],cum_weights=[2/3,5/6,1],k=15)
[-10, 50, -10, 50, 50, -10, 3, -10, -10, -10, -10, 50, -10, 3, -10]Si l’on veut récupérer le tableau des effectifs :
def loi_discrete_choices(X,P,n):
L=choices(X,cum_weights=P,k=n)
l=len(X)
S=[0]*l
for i in range(l):
S[i]=L.count(X[i])
return SUtilisation :
>>> loi_discrete_choices([-10,3,50],[2/3,5/6,1],1000)
[663, 180, 157]Et si l’on veut les fréquences, on remplace S[i]=L.count(X[i]) par S[i]=L.count(X[i])/n
Utilisation :
>>> loi_discrete_choices([-10,3,50],[2/3,5/6,1],1000)
[0.694, 0.15, 0.156]Avec les poids initiaux :
Pour simuler la loi discrète :
>>> from random import *
>>> choices([-10,3,50],[2/3,1/6,1/6],k=1)
[3]Et pour simuler n expériences :
>>> choices([-10,3,50],[2/3,1/6,1/6],k=15)
[3, 3, -10, 50, 3, -10, 3, 3, -10, 3, 50, -10, -10, 50, -10]Si l’on veut récupérer le tableau des effectifs :
def loi_discrete_choices(X,P,n):
L=choices(X,P,k=n)
l=len(X)
S=[0]*l
for i in range(l):
S[i]=L.count(X[i])
return SUtilisation :
>>> loi_discrete_choices([-10,3,50],[2/3,1/6,1/6],1000)
[663, 180, 157]Et si l’on veut les fréquences, on remplace S[i]=L.count(X[i]) par S[i]=L.count(X[i])/n
Utilisation :
>>> loi_discrete_choices([-10,3,50],[2/3,1/6,1/6],1000)
[0.694, 0.15, 0.156]Fonction Python renvoyant une moyenne pour un échantillon. Série des moyennes pour N échantillons de taille n d’une variable aléatoire d’espérance μ et d’écart type σ. Calcul de l’écart type s de la série des moyennes des échantillons observés,à comparer à σ/√n. Calcul de la proportion des cas où l’écart entre m et μ est inférieur ou égal à kσ/√n ou à ks, pour k=2 ou k=3.
On simule des échantillons de taille N d’une variable aléatoire X suivant une loi discrète uniforme dans $\{1 ; 2 ; ... ; n\}$ (cela revient à lancer un dé équilibré à n faces) :
from random import *
def echantillon(N,n):
L=[]
for i in range(N):
L.append(randint(1,n))
return LUtilisation :
>>> echantillon(10,8)
[6, 4, 2, 2, 4, 1, 8, 8, 7, 8]On peut alors s’intéresser à la moyenne de cet échantillon :
def moyenne(L):
return sum(L)/len(L)Et constater qu’en général la moyenne obtenue n’est pas égale à l’espérance :
>>> moyenne(echantillon(10,8))
3.9$E(X)=\frac{n+1}{2}$.
Dans notre exemple $E(X) = \frac{9}{2} = 4,5 \neq 3,9$.
Pour comprendre ce phénomène, on peut simuler des échantillons de taille n et calculer la moyenne de ces échantillons :
def SerieMoyennes(NS,N,n):
M=[]
for i in range(NS):
M.append(moyenne(echantillon(N,n)))
return MUtilisation :
>>> SerieMoyennes(20,1000,8)
[4.468, 4.526, 4.365, 4.605, 4.512, 4.536, 4.538, 4.534, 4.547, 4.462, 4.418, 4.493, 4.534, 4.509, 4.466, 4.493, 4.523, 4.457, 4.324, 4.338]On n’obtient pas une seule fois 4,5 sur ces 20 séries mais la taille des échantillons étant assez grande, on trouve des moyennes « proches » de 4,5.
On va alors s’intéresser à cette notion de proximité en calculant l’écart-type :
from math import *
def EcartType(L):
n=len(L)
m=moyenne(L)
ET=[]
for i in range(n):
ET.append((L[i]-m)**2)
v=moyenne(ET)
s=sqrt(v)
return sPuis la proportion de ces moyennes m qui appartiennent aux intervalles $[\mu - \frac{k\sigma}{\sqrt{N}} ; \mu + \frac{k\sigma}{\sqrt{N}}]$ :
def prop_int_ksigma(NS,N,n,k):
e=0
S=SerieMoyennes(NS,N,n)
mu=(1+n)/2
sigma=EcartType(S)
for m in S:
if abs(m-mu)<k*sigma/sqrt(N):
e=e+1
return e/NUtilisation :
>>> prop_int_ksigma(1000,500,8,1)
0.084
>>> prop_int_ksigma(1000,500,8,2)
0.118
>>> prop_int_ksigma(1000,500,8,3)
0.192Simulation d’une variable aléatoire de loi géométrique à partir du schéma de Bernoulli.
Définition : Soit $0 < p < 1$. On dit qu’une variable $X$ suit une loi géométrique de paramètre $p$, notée $G(p)$ si
a) $X$ est à valeurs dans $\mathbb{N}^{{}∗{}}$ ;
b) $∀k≥1, P(N=k) = (1−p)^{k−1}p$.
La variable aléatoire qui suit une loi géométrique de paramètre $p$ peut être assimilée au temps d’attente du premier succès d’un schéma de Bernoulli :
from random import random
def attente_succes(p):
temps_attente=1
alea=random()
while alea>p:
alea=random()
temps_attente+=1
return temps_attenteUtilisation :
>>> attente_succes(0.2)
3
>>> attente_succes(0.2)
10
>>> attente_succes(0.2)
1
>>> attente_succes(0.2)
4
>>> attente_succes(0.2)
23On peut alors simuler un grand nombre de fois l’expérience et représenter graphiquement le résultat :
from random import random
import matplotlib.pyplot as pyplot
def attente_succes(p):
temps_attente=1
alea=random()
while alea>p:
alea=random()
temps_attente+=1
return temps_attente
def simulation(p,N):
liste_nbtirages=[0]*30
for i in range(N):
t=attente_succes(p)
if t<=30:
liste_nbtirages[t-1]+=1
pyplot.xlabel("Nombde de tentatives avant le succès")
pyplot.ylabel("Effectifs")
pyplot.bar(range(1,31),liste_nbtirages,width=0.5,color="blue")
pyplot.show()Utilisation :
>>> simulation(0.2,100000)

On peut aussi afficher le résultat théorique :
def loi_geom(p,k):
K=[k for k in range(1,k+1)]
P=[p*(1-p)**(k-1) for k in range(1,k+1)]
pyplot.xlabel("Nombre de tentatives avant le succès")
pyplot.ylabel("Probabilité")
pyplot.bar(K,P)
pyplot.show()Utilisation :
>>> loi_geom(0.2,30)

Simulation d’une loi exponentielle à partir d’une loi uniforme.
On peut simuler la loi uniforme sur l’intervalle [a ; b] à l’aide de la fonction random() du module random :
from random import random
def uniforme(a,b):
return(a+(b-a)*random())En effet random() renvoie un nombre aléatoire de l’intervalle [0 ; 1[ (La suite de nombres générée “ressemble” à une suite de variables aléatoires uniformes et indépendantes.), donc (b-a)*random() renvoie un nombre aléatoire de l’intervalle [0 ; b-a[ et a+(b-a)*random() renvoie un nombre aléatoire de l’intervalle [a ; b[ .
La fonction densité de probabilité de cette loi uniforme sur [a ; b] est une fonction constante par morceaux :
def densuni(x,a,b):
#densité sur [a,b]
if (a<=x and x<=b):
return(1/(b-a))
else:
return(0)Et si l’on veut sa représentation graphique :
import numpy as np
import matplotlib.pyplot as plt
from random import random
def uniforme(a,b):
return(a+(b-a)*random())
def densuni(x,a,b):
#densité sur [a,b]
if (a<=x and x<=b):
return(1/(b-a))
else:
return(0)
def graph_uniforme(a,b):
abs=np.linspace(a-(b-a),b+(b-a),200)
y=[densuni(x,a,b) for x in abs]
plt.grid()
plt.plot(abs,y)
plt.show()Utilisation :
>>>graph_uniforme(-5,10)

On peut aussi s’intéresser à la fonction de répartition :
def repartuni(x,a,b):
#fonction de répartition sur [a,b]
if x<a:
return(0)
elif (a<=x and x<=b):
return((x-a)/(b-a))
else:
return(1)
def graph_repartuniforme(a,b):
abs=np.linspace(a-(b-a),b+(b-a),200)
y=[repartuni(x,a,b) for x in abs]
plt.grid()
plt.plot(abs,y)
plt.show()Utilisation :
>>>graph_repartuniforme(-5,10)

Pour la loi exponentielle de paramètre λ, on a $F(x) = 1−e^{−λx}$ pour $x \geqslant 0$ et $F(x) = 0$ si $x \lt 0$. Sur $\mathbb{R}+$ , la fonction F(x) est continue et strictement croissante, on a l’équivalence :
$u = 1−e^{−λx} \Leftrightarrow 1 - u = e^{−λx} \Leftrightarrow ln(1 - u) = −λx \Leftrightarrow x = F^{−1}(u) =−\frac{1 }{λ}ln(1−u)$.
On peut donc simuler X à partir de U puisque $F^{−1}(U)$ suit la même loi que X.
On peut alors écrire une fonction Expo qui prend en argument un réel a>0 et renvoie une réalisation d’une variable aléatoire qui suit la loi Exponentielle de paramètre a :
from math import log
from random import *
def Expo(a):
return -1/a*log(1-random())Utilisation :
>>>Expo(2)
>>>0.5242804058215232
>>>Expo(0.2)
>>>3.2637966061217183On peut alors utiliser une fonction qui va procéder à un nombre n de tirages aléatoires :
def tirages(n,a):
L=[]
for i in range(n):
L.append(Expo(a))
return LUtilisation :
>>>tirages(10,0.3)
>>>[1.4373901275636258,
4.961359207330598,
1.5097403973808872,
5.805058647163496,
9.818932947901471,
11.037823931384885,
1.3647856789399562,
3.4588250161094725,
2.9218462025078207,
4.015415133657791]On peut alors passer à la représentation graphique en utilisant la commande hist [2] du module matplotlib :
def graphe(n,a):
L=tirages(n,a)
maxL=int(max(L))
hist(L , bins = 100, range=(0,maxL), normed = True)

On peut alors compléter le graphique avec la densité théorique $f(x)=ae^{−a x}$.
from matplotlib.pyplot import *
from random import *
from math import log,exp
def Expo(a):
return -1/a*log(1-random())
def tirages(n,a):
L=[]
for i in range(n):
L.append(Expo(a))
return L
def graphe(n,a):
L=tirages(n,a)
maxL=int(max(L))
hist(L , bins = 100, range=(0,maxL), normed = True)
x = [float(i)/100 for i in range(100*maxL)]
f = [a*exp(-a*t) for t in x]
plot(x,f)
graphe(10000,0.5)

Enfin l’on peut s’intéresser à la fonction de répartition, que l’on peut simuler avec un histogramme des effectifs cumulés croissants de densité 1 :
def repartition(n,a):
L=tirages(n,a)
maxL=int(max(L))
hist(L , bins = 100, range=(0,maxL), density = True,cumulative=True)
show()Utilisation :
>>> repartition(10000,0.4)

On peut alors compléter le graphique avec la fonction de répartition théorique $F(x)=1−e^{−ax}$.
Il y a un paramètre dans la commande hist de matplotlib : cumulative=True qui permet d’avoir les Effectifs Cumulés Croissants et avec density=True on a les Fréquences Cumulées Croissantes, donc la fonction de répartition.
def repartition(n,a):
L=tirages(n,a)
maxL=int(max(L))
hist(L , bins = 100, range=(0,maxL), density = True,cumulative=True)
x = [float(i)/100 for i in range(100*maxL)]
f = [1-exp(-a*t) for t in x]
plot(x,f)
show()Utilisation :
>>> repartition(50000,3)

Demi-vie d’un échantillon de grande taille d’atomes radioactifs.
Décroissance radioactive :
Pour simuler le caractère aléatoire de la désintégration d’un noyau individuel, on peut simuler à l’aide d’un programme Python, si l’on connait la probabilité p de désintégration d’un noyau, on utilise une variable aléatoire qui, si elle est inférieure à p élimine le noyau. Pour travailler sur un échantillon, on fait cela pour n noyaux.
from random import *
def compte_noyaux_restants(n,p):
N=n
for i in range(n):
if random() < p :
N=N-1
return NUtilisation :
>>> compte_noyaux_restants(10000,0.02)
9821On peut alors réitérer cela jusqu’á ce qu’il n’y ait plus de noyaux (En fait on s’arrêtera lorsqu’il en reste moins de 1%) :
def Liste_nb_noyaux_restants(n,p):
L=[]
N=n
while n>0.01*N:
L.append(n)
n=compte_noyaux_restants(n,p)
return LUtilisation :
>>> Liste_nb_noyaux_restants(10000,0.02)
[10000, 9802, 9606, 9417, 9240, 9069, 8886, ...., 111, 108, 106, 102, 102]Et la représentation graphique :
import matplotlib. pyplot as plt
def simule_desintegration(n,p):
L=Liste_nb_noyaux_restants(n,p)
plt.plot(range(len(L)),L, linestyle ="none",marker=".")
plt.show()
simule_desintegration(10000,0.03)

Demi-vie :
La demi-vie d’un noyau radioactif, également appelée période radioactive, est la durée nécessaire pour que la moitié des noyaux initialement présents dans un échantillon macroscopique se soit désintégrée. En raison de l’absence de vieillissement, cette demi-vie, caractéristique du noyau considéré, est indépendante de l’instant initial. La demi-vie est, généralement, notée $T_{\frac{1}{2}}$.
def demi_vie(N,p):
n=N
i=0
while n>N/2:
i+=1
n=compte_noyaux_restants(n,p)
return iUtilisation :
>>> demi_vie(10000,0.03)
23
>>> demi_vie(1000,0.02)
36
>>> demi_vie(10000,0.02)
35Datation au carbone 14 :
Les organismes vivants contiennent naturellement du carbone 14 ($^{14}C$) provenant de l’interaction des rayons cosmiques avec le carbone présent dans l’atmosphère. La proportion de $^{14}C$ par rapport au $^{12}C$ présent dans un organisme vivant est constante, égale à $1,3\times 10^{-12}$. À la mort d’un organisme, les échanges avec l’atmosphère cessent. Le carbone 14 qu’il contient se désintègre à raison de 12 pour 1000 tous les 100 ans, alors que le $^{12}C$ n’évolue pas.
La demi-vie du $^{14}C$ est d’environ 5800 ans (5 730 ± 40 ans selon Wikipedia) :
>>> demi_vie(100000,12/1000)
58
>>> demi_vie(100000,12/100000)
5794La méthode la plus courante de datation consiste à déterminer la concentration $C_t$ de radiocarbone (c’est-à-dire le rapport $\frac{^{14}C}C_{total}$) d’un échantillon à l’instant $t$ de mesure ; l’âge de l’échantillon est alors donné par la formule : $t − t_0 = \frac{1}{λ}\times ln \frac{C_0}{C_t}$ où ${C}_{0}$ est la concentration de radiocarbone de l’échantillon à l’instant $t_0$ de la mort de l’organisme d’où provient l’échantillon $\left(C_0 \approx 1.3\times 10^{− 12}\right)$ et λ la constante radioactive du carbone 14$\left(\lambda = \frac {\ln 2}{t_{\frac {1}{2}}} \approx 1,210\cdot 10^{-4} {an} ^{-1}\right)$.
D’où l’algorithme :
from math import log
def datation_C14(p):
C0=1.3*10**(-12)
lamb=1.21*10**(-4)
return round(1/lamb*log(C0/p))Des archéologues ont trouvé des fragments d’os dans lesquels la proportion de carbone 14 par rapport au carbone 12 est égale à $7\times 10^{-13}$. Estimer l’âge de ces fragments d’os.
>>> datation_C14(7*10**(-13))
5116On a découvert dans une grotte en Dordogne un foyer contenant du charbon de bois. À quantité égale, un morceau de bois actuel contient 1,5 fois plus de $^{14}C$ que le charbon de bois prélevé dans la grotte. Estimer une datation de l’occupation de la grotte.
>>> datation_C14(1.3*10**(-12)/1.5)
3351Lorsque la teneur en carbone 14 d’un organisme devient inférieure à 0,3 % de sa valeur initiale, on ne peut plus dater précisément à l’aide du carbone 14. Déterminer l’âge à partir duquel un organisme ne peut plus être daté au carbone 14.
>>> datation_C14(0.3/100*1.3*10**(-12))
48009Sur des exemples, résolution approchée d’une équation différentielle par la méthode d’Euler.
Résolution par la méthode d’Euler de $y’ = y$, et de $y’ = ay + b$.
En mathématiques, la méthode d’Euler est une procédure numérique pour résoudre par approximation des équations différentielles du premier ordre avec une condition initiale. C’est la plus simple des méthodes de résolution numérique des équations différentielles.
Pour h proche de 0, on a $y(a+h) \approx y(a) + h y’(a)$ .Nous allons utiliser cette approximation affine pour construire pas à pas une fonction vérifiant une équation différentielle du premier ordre et passant par un point donné $(x_0 ; y_0)$.
Soit l’équation différentielle définie par $y’=y$ et les conditions initiales $(x_0 ; y_0)$. En $(x_0 ; y_0)$, on connaît la pente de la tangente à partir de l’équation différentielle, $y_0$. On assimile alors sur l’intervalle $[x_0 ; x_0 + h]$ la fonction à sa tangente. On détermine alors le point $(x_1 ; y_1)$ avec $x_1 = x_0 + h$ et $y_1 = y_0 + hy_0 = y_0(1 + h)$. On recommence le même raisonnement avec le point $(x_1 ; y_1)$. On poursuit en construisant la suite de points $(x_n ; y_n)$ et en assimilant la courbe à une application affine par morceaux.
def Euler(x0,xf,y0,n):
x=x0
y=y0
h=(xf-x0)/float(n)
abscisse=[x0]
ordonnee=[y0]
for i in range(n):
x=x+h
y=y*(1+h)
abscisse.append(x)
ordonnee.append(y)
return ordonneeUtilisation :
>>> Euler(0,3,1,30)
[1, 1.1, 1.2100000000000002, 1.3310000000000004, 1.4641000000000006, 1.6105100000000008, 1.771561000000001,
1.9487171000000014, 2.1435888100000016, 2.357947691000002, 2.5937424601000023, 2.853116706110003,
3.1384283767210035, 3.4522712143931042, 3.797498335832415, 4.177248169415656, 4.594972986357222,
5.054470284992944, 5.559917313492239, 6.115909044841463, 6.72749994932561, 7.400249944258172, 8.140274938683989,
8.954302432552389, 9.849732675807628, 10.834705943388391, 11.91817653772723, 13.109994191499954,
14.420993610649951, 15.863092971714948, 17.449402268886445]Le graphique ci-dessous est réalisé avec les données ci-dessus et les valeurs exactes.

Soit l’équation différentielle définie par $y’= ay + b$ et les conditions initiales $(x_0 ; y_0)$. En $(x_0 ; y_0)$, on connaît la pente de la tangente à partir de l’équation différentielle, $ay_0 + b$. On assimile alors sur l’intervalle $[x_0 ; x_0 + h]$ la fonction à sa tangente. On détermine alors le point $(x_1 ; y_1)$ avec $x_1 = x_0 + h$ et $y_1 = y_0 + h (ay_0 + b)$. On recommence le même raisonnement avec le point $(x_1 ; y_1)$. On poursuit en construisant la suite de points $(x_n ; y_n)$ et en assimilant la courbe à une application affine par morceaux.
def Euler(x0,xf,y0,n,a,b):
x=x0
y=y0
h=(xf-x0)/float(n)
abscisse=[x0]
ordonnee=[y0]
for i in range(n):
x=x+h
y=y+h*(a*y+b)
abscisse.append(x)
ordonnee.append(y)
return ordonneeUtilisation :
>>> Euler(0,3,2,30,-0.5,0)
[2, 1.9, 1.805, 1.71475, 1.6290125, 1.547561875, 1.47018378125, 1.3966745921875001, 1.3268408625781252,
1.2604988194492188, 1.1974738784767578, 1.13760018455292, 1.080720175325274, 1.0266841665590103,
0.9753499582310597, 0.9265824603195068, 0.8802533373035314, 0.8362406704383548, 0.7944286369164371,
0.7547072050706152, 0.7169718448170844, 0.6811232525762302, 0.6470670899474187, 0.6147137354500477,
0.5839780486775453, 0.5547791462436681, 0.5270401889314846, 0.5006881794849104, 0.4756537705106649,
0.45187108198513165, 0.4292775278858751]

Et l’on peut généraliser le processus :
Soit l’équation différentielle définie par $y’=f(x,y)$ et les conditions initiales $(x_0 ; y_0)$. En $(x_0 ; y_0)$, on connaît la pente de la tangente à partir de l’équation différentielle, $f(x_0 ; y_0)$. On assimile alors sur l’intervalle $[x_0 ; x_0 + h]$ la fonction à sa tangente. On détermine alors le point $(x_1 ; y_1)$ avec $x_1 = x_0 + h$ et $y_1 = y_0 + hf(x_0,y_0)$. On recommence le même raisonnement avec le point $(x_1 ; y_1)$. On poursuit en construisant la suite de points $(x_n ; y_n)$ et en assimilant la courbe à une application affine par morceaux.
La fonction « Euler » ci-dessous prend comme dernier argument une fonction de deux variables :
def Euler(x0,xf,y0,n,f):
x=x0
y=y0
h=(xf-x0)/float(n)
abscisse=[x0]
ordonnee=[y0]
for i in range(n):
x=x+h
y=y+h*f(x,y)
abscisse.append(x)
ordonnee.append(y)
return ordonneeOn peut tester la fonction précédente avec f définie par f(x,y)=-0.5y :
>>> def f(x,y):
... return -0.5*y
...
>>> Euler(0,3,2,30,f)
[2, 1.9, 1.805, 1.71475, 1.6290125, 1.547561875, 1.47018378125, 1.3966745921875001, 1.3268408625781252,
1.2604988194492188, 1.1974738784767578, 1.13760018455292, 1.080720175325274, 1.0266841665590103,
0.9753499582310597, 0.9265824603195068, 0.8802533373035314, 0.8362406704383548, 0.7944286369164371,
0.7547072050706152, 0.7169718448170844, 0.6811232525762302, 0.6470670899474187, 0.6147137354500477,
0.5839780486775453, 0.5547791462436681, 0.5270401889314846, 0.5006881794849104, 0.4756537705106649,
0.45187108198513165, 0.4292775278858751]Ce qui donne bien le résultat précédent comme on s’y attendait.
Simulation d’une variable de Bernoulli ou d’un lancer de dé (ou d’une variable uniforme sur un ensemble fini) à partir d’une variable aléatoire de loi uniforme sur [0,1].
Simulation d’une variable de Bernoulli
Une épreuve de Bernoulli a deux issues de probabilités $p$ et $1-p$.
La fonction epreuve() ci-dessous simule une épreuve de Bernoulli :
from random import random
def epreuve(p):
if random()<=p:
return True
else:
return FalseLa fonction schema() ci-dessous simule un schéma de Bernoulli, elle renvoie le nombre de succés lors de n épreuves de Bernoulli :
def schema(n,p):
nb_succes=0
for i in range(n):
if epreuve(p)==True:
nb_succes+=1
return nb_succesPour la simulation de N schémas de Bernoulli avec stockage de la fréquence du succès, on utilisera la fonction experience() ci-dessous :
def experience(N,n,p):
frequences=[]
for i in range(N):
frequences.append(0)
for i in range(N):
nb_succes=schema(n,p)
frequences[i]=nb_succes/n
return frequencesUtilisation :
>>> experience(10,1000,0.4)
[0.4, 0.389, 0.394, 0.406, 0.399, 0.4, 0.401, 0.404, 0.386, 0.415]Simulation d’un lancer de dé
from random import random
def lancer_de(n):
de=[0]*6
for i in range(n):
valeur=random()
if valeur<=1/6:
de[0]+=1
elif valeur<=2/6:
de[1]+=1
elif valeur<=3/6:
de[2]+=1
elif valeur<=4/6:
de[3]+=1
elif valeur<=5/6:
de[4]+=1
else:
de[5]+=1
return deUtilisation :
>>> lancer_de(1000)
[177, 177, 143, 170, 178, 155]Simulation du comportement de la somme de n variables aléatoires indépendantes et de même loi.
Soit n un nombre entier naturel supérieur ou egal à 2. $X_1, X_2, ... , X_n$ sont des variables aléatoires qui suivent la loi uniforme sur [0 ; 1].
Soit Y la variable aléatoire qui prend toutes les valeurs $x_1 + x_2 + ... + x-n$ correspondant à la somme des valeurs prises par $X_1, X_2, ... , X_n$. Y est donc à valeur dans [0 ; n], quelle est la loi suivie par Y ?
On peut utiliser une fonction Python pour simuler cette variable aléatoire :
from random import *
def somme(N,n):
L=[0]*n
for i in range(N):
x=0
for k in range(n):
x=x+random()
x=int(x)
L[x]+=1
for r in range(n):
L[r]=L[r]/1000
return LAprès avoir sommé les n valeurs, on les arrondit afin d’obtenir des effectifs pour n valeurs discrètes. On peut ensuite tracer l’allure de la fonction de répartition de Y :
from random import *
import matplotlib.pyplot as pyplot
def somme(N,n):
L=[0]*n
for i in range(N):
x=0
for k in range(n):
x=x+random()
x=round(x)
L[x]+=1
for r in range(n):
L[r]=L[r]/1000
A=[k for k in range (n)]
pyplot.bar(A,L,width=0.5,color="blue")
pyplot.show()
return LUtilisation :
>>> somme(1000,16)
[0, 0, 0, 0, 3, 43, 142, 349, 279, 147, 35, 2, 0, 0, 0, 0]
[0.0, 0.0, 0.0, 0.0, 0.003, 0.043, 0.142, 0.349, 0.279, 0.147, 0.035, 0.002, 0.0, 0.0, 0.0, 0.0]

Version 2 en utilisant la fonction hist de matplotlib :
from random import *
import matplotlib.pyplot as pyplot
def somme2(N,n):
L=[]
for i in range(N):
x=0
for k in range(n):
x=x+random()
L.append(x)
pyplot.hist(L,bins=100,range=(1,n+1))
pyplot.show()Utyilisation :
>>> somme2(1000,16)