Olivier Leguay est l’auteur de Maths 2.0 et intégration de pratiques 2.0 dans l’enseignement des mathématiques dans MathémaTICE.
Dans l’article qui suit, il remet en cause l’incroyable naïveté qui a conduit à considérer comme facile et naturelle l’usage des technologies dans l’enseignement. Il montre ici, à partir de Geogebra, tout ce qu’implique pour l’enseignant l’intégration véritable d’un logiciel dans sa pratique usuelle.
Mais surtout, il offre aux collègues qui le souhaitent l’auto-formation à Geogebra « qu’il aurait aimé trouver pour faciliter son apprentissage isolé et pour lui faire gagner du temps ».
Des TUICE ?
Et si le problème des TICE avait été mal posé au départ ? Peut-être aurait-on mis un peu trop définitivement l’élève au centre du processus et oublié au passage l’enseignant. La première dénomination « TICE » pour Technologies de l’Information et de la Communication dans l’Enseignement avait oublié la lettre « U » de « Usuelles », lettre qui marque sans doute le passage le plus délicat du processus technologique pour l’enseignant : celui d’intérioriser et d’intégrer les TICE de façon « Usuelle » dans son enseignement et de les transformer ainsi en TUICE.
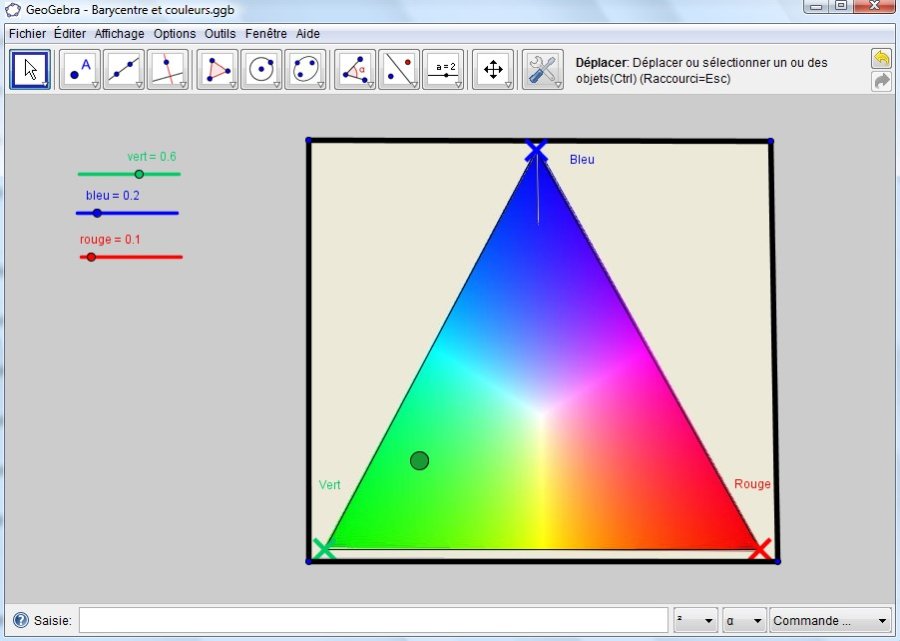
Pour prendre l’exemple de GeoGebra, le débat a été placé initialement sur le fait que c’était un logiciel de géométrie dynamique et qu’il devait être utilisé par l’élève avec cette dénomination. On y voyait alors l’instrument de découverte de la figure géométrique, du lieu géométrique et de la construction de figures dynamiques, avec ses partisans et ses détracteurs, dont les débats ont été fournis lors de l’instauration de l’Epreuve Pratique. GeoGebra devait être considéré comme un successeur possible de Geoplan ou de Cabri. C’était en fait la partie visible de l’iceberg, la plus accessible. Le débat, incomplet et décalé, masquait celle qui se trouvait sous l’eau, dépassant de loin cette seule utilisation pédagogique. Pour l’élève, la vision du logiciel ne peut plus se réduire à la réalisation de quelques questions d’exercices, parfois très artificielles, ou des TP donnés par le professeur commençant la plupart du temps par : « En utilisant un logiciel de géométrie dynamique…. ». Il doit plutôt y voir un formidable outil, un « stylo » très efficace, qu’il peut et doit utiliser de façon autonome pour la réalisation de tâches variées (réalisation de graphiques, émission de conjectures, zoom, utilisation de curseurs pour les paramètres, calculs, modifications de coefficients et de positions, vérification de résultats, réalisation de figures claires, impressions pertinentes, raisonnements argumentés, visualisations diverses). Je ne fais pas ici l’apologie de GeoGebra en particulier, mais je donne la vision intériorisée que devrait avoir un élève, d’un logiciel lui permettant de faire et de comprendre des mathématiques. Le professeur, de son coté, ne devrait pas voir exclusivement la seule composante d’utilisation des TICE indiquée dans les programmes officiels. Il devrait pouvoir intégrer naturellement l’utilisation d’un tel logiciel dans sa pratique quotidienne, pour l’aider, appuyer son argumentation, rendre son cours plus visuel, plus clair et plus dynamique et il devrait aussi être en mesure de proposer en ligne les contenus visualisés en classe afin d’être récupérés et utilisés par les élèves.
Il y a cependant entre ces deux visions et mises en pratique, un saut temporel, matériel, organisationnel, technique, didactique et pédagogique considérable qui demande une formation longue qu’elle soit en autodidaxie ou non. Comment a-t-on pu penser que la transposition d’un tel outil, et d’une façon plus générale, des TICE dans l’enseignement, pourrait se faire de façon naturelle, alors que toute volonté de transmission, de modification du théâtre pédagogique, met au grand jour des freins toujours plus nombreux ? Pourquoi en aurait-il été différemment ici ? La tâche est immense et dépasse de loin le seul travail du professeur isolé, car il doit être en mesure de les intégrer dans les situations existantes, de leur trouver une place, une utilité, sans quoi leur introduction ne créerait aucun nouveau bénéfice. Des nouvelles situations pédagogiques doivent être imaginées où le support ne serait plus seulement le livre ou le polycopié, permettant ainsi une généralisation de l’utilisation quotidienne des outils logiciels en cours.
Il n’y a qu’en mettant le pied à l’étrier que l’on peut concevoir l’étendue des possibles, des besoins et des obstacles et comme l’a si bien dit Clairaut :
« En suivant cette voie, les Commençans apperçoivent, à chaque pas qu’on leur fait faire, la raison qui détermine l’Inventeur, & par là ils peuvent acquérir plus facilement l’esprit d’invention. ».
Au quotidien
Nous supposerons au départ que nous disposons pour la promenade, dans notre sac à dos, d’un ordinateur en classe et d’un vidéoprojecteur raccordé, configuration minimale sans laquelle il ne sera pas possible d’aller plus loin. La connexion Internet serait un plus mais elle ne sera pas obligatoire dans la version TUICE de base. Il n’est pas utile de discuter plus longuement du fait que la réalité de cette configuration matérielle « de base » pose elle-même de nombreuses difficultés, mais il serait vain d’y consacrer plus de temps ici et cela ne ferait en rien avancer les problèmes associés (existence et maintenance).
Plus que des réponses toutes faites, ce seront les premières interrogations qui permettront les avancées.
C’est le début de la journée et les interrogations subsistent, toujours présentes : Est-ce que ça va fonctionner ? Combien de temps ça va me prendre ? Est-ce que je vais être capable de gérer l’imprévu ? Est-ce que l’idée que j’ai eue sera la bonne ? Est-ce vraiment utile ? A quoi bon y avoir passé tant de temps ?
La cloche sonne. Quelques minutes après, les élèves sont en binôme devant un ordinateur. Le travail d’optimisation n’est pas si évident que cela…
La cloche sonne. Quelques minutes après, le professeur construit petit à petit la figure sur le tableau blanc. Elle est nette et il est possible d’y apporter des modifications. Les élèves la reproduisent sur leur cahier, peuvent la modifier sur le tableau, le professeur l’utilisera pendant son exposé. Les élèves pourront s’y référer pour en reconstruire une similaire pendant une séance devant l’ordinateur.
La cloche sonne. Quelques minutes après, le fichier préparé la veille est projeté. Il contient une animation sur laquelle le début du cours s’appuie. Un autre contient toutes les formules du cours que l’on affichera à loisir.
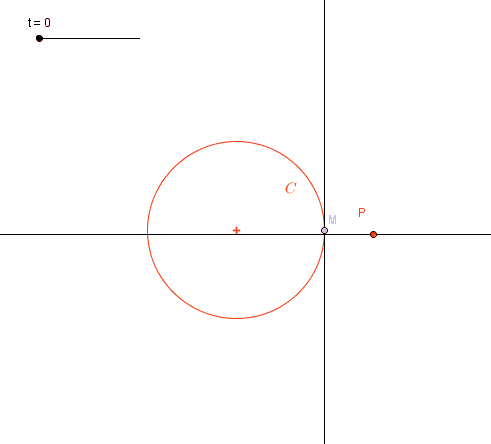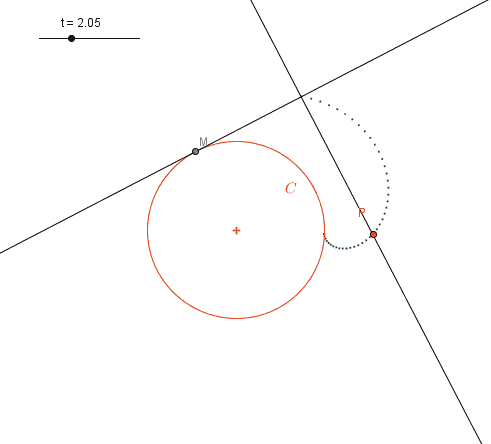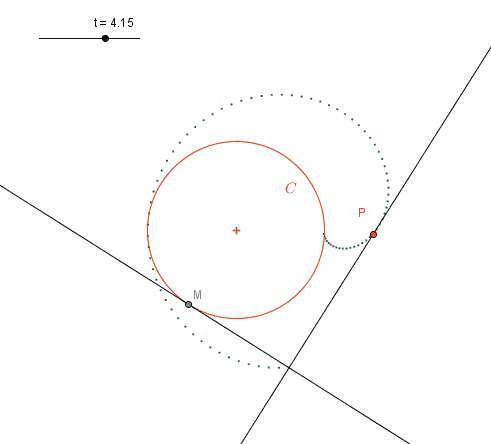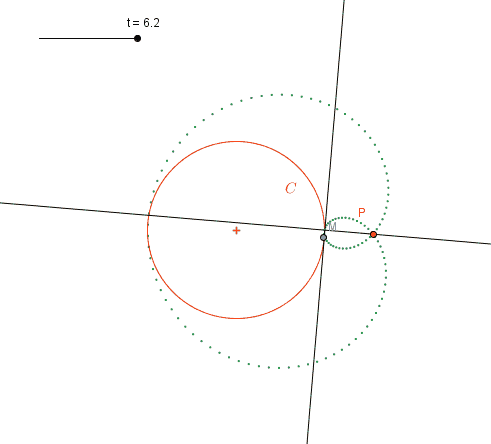
La cloche sonne. Quelques minutes après, la courbe de la fonction de l’exercice précédent s’est transformée en une autre, puis est apparue celle d’une fonction de référence, et puis une autre dont le signe n’est pas si évident. Le signe de la fonction associée à la courbe verte correspond aux variations de celle associée à la rouge….
La cloche sonne et le cours est terminé. Les élèves rentrent chez eux et ils pourront retrouver en ligne les différentes animations présentées en cours et les imprimer.
Entre le premier son de cloche et le dernier, plus de quinze ans se sont écoulés. En débutant dans le métier, il m’a été assez simple et rapide de placer les élèves devant un ordinateur. Le passage aux TUICE a été le fruit d’un long travail de compréhension et d’une autodidaxie intégrale. Les difficultés techniques sont une partie seulement de celles rencontrées. Une fois levées, bien d’autres persistent. Elles sont d’ordre pédagogique et didactique. C’est l’aspect technique qui est visité sur le blog « Autour de Geogebra » afin de permettre une assimilation plus rapide, de faire émerger des idées qui elles mêmes en donneront d’autres.
« Autour de GeoGebra »
La présentation de GeoGebra comme logiciel de géométrie dynamique l’a placé de fait entre les mains de l’élève, interdisant toute réflexion sur sa prise en main et son utilisation par le professeur dans la majorité de ses cours. Les deux problématiques ne sont pourtant pas si proches. Créer une activité intéressante autour d’un logiciel mis entre les mains d’un élève n’a que peu de choses à voir avec l’utilisation de ce logiciel par l’enseignant.
L’élève devra bien souvent effectuer des commandes simples pour accéder à des situations complexes alors que pour l’enseignant la démarche est presque inverse. Il devra effectuer des commandes complexes pour simplifier une notion, améliorer la compréhension, amener à la visualisation, à la représentation, rendre le contenu dynamique.
Un exemple simple est celui de l’affichage de caractères mathématiques et d’informations dynamiques :
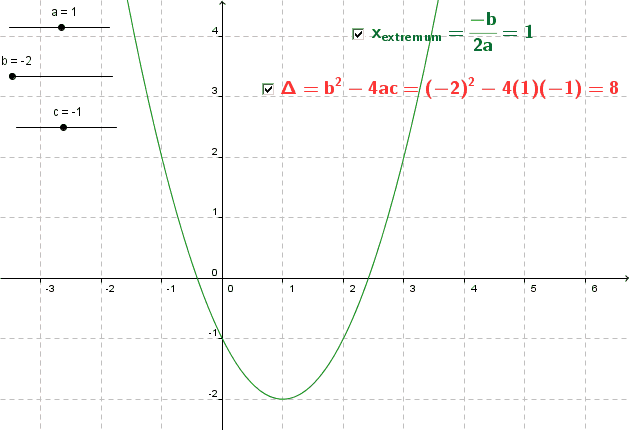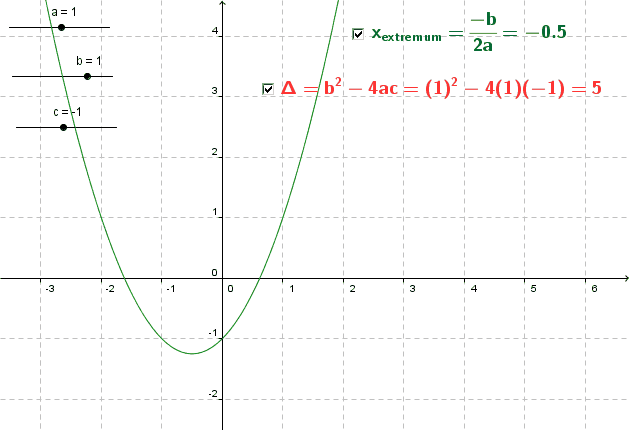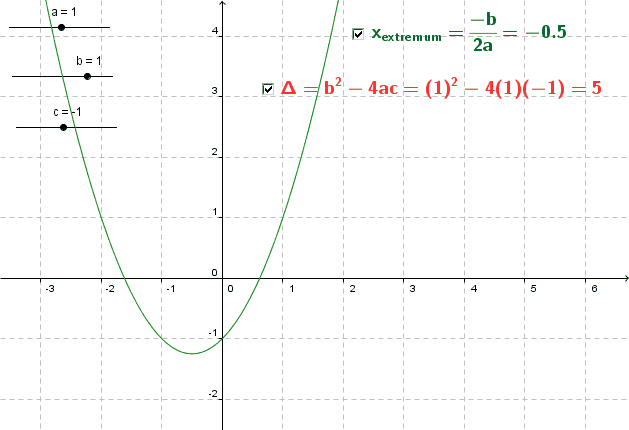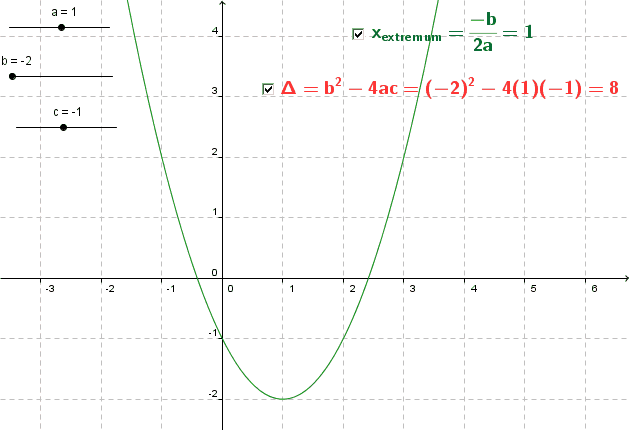
Une case à cocher pour afficher/masquer, trois curseurs et un affichage dynamique du discriminant. Cette petite configuration est impossible à réaliser au pied levé sans « formation » sur le logiciel. Il est possible de la réaliser en moins de cinq minutes avec un peu d’habitude. Mais pour cela il aura fallu visiter l’utilisation des curseurs, l’affichage conditionnel, l’écriture avec Latex et l’affichage dynamique.
Le blog « Autour de Geogebra » est constitué de tutoriels et d’exercices. Les tutoriels sont dans une grande majorité des cas construits de façon similaire : une vidéo sans son et le fichier GeoGebra présenté téléchargeable. Il m’a semblé inutile d’adjoindre le son, l’image étant largement explicative pour les procédures présentées. On peut par exemple découvrir dans un tutoriel des manipulations très simples, comme
- l’utilisation d’un curseur
- des techniques plus avancées telles que l’utilisation de la commande « Séquence »
- des manipulations extérieures au logiciel : l’implantation de l’applet sur un blog
- l’utilisation de Javascript
Ces tutoriels permettent par autodidaxie, l’obtention d’un niveau de maîtrise suffisant du logiciel pour son propre usage.
Ils ne sont en aucun cas destinés à parcourir de façon exhaustive toutes les commandes du logiciel mais plutôt à développer une vision interne de sa manipulation. Pour les constructions les plus rapides, il peut être intéressant de se fixer comme objectif l’utilisation du logiciel en cours, « en direct » devant élèves. Il peut être aussi intéressant de montrer et d’expliquer des commandes de base aux élèves, ou de leur donner les moyens de retrouver par eux-mêmes les procédures dont ils pourront avoir le plus besoin (par exemple en ce qui concerne les fonctions).
Les exercices proposés dans le blog sont des bases de réflexion. Ils permettent de voir si l’on est en mesure ou non de réaliser le fichier proposé. Les difficultés ne sont pas nécessairement là où on les attend. Ils ne sont pas classés par ordre croissant de difficulté. Ce ne sont pas des exercices mathématiques, mais bel et bien des exercices sur la manipulation du logiciel. L’objectif est d’amener l’enseignant à l’autonomie dans la réalisation de fichiers GeoGebra selon ses propres besoins. L’exercice associé au calcul de la distance de deux points du plan est en outre, tout à fait utilisable en cours. Il est rapide. D’autres exercices permettent le réinvestissement direct d’une notion expliquée dans un tutoriel. Certains exercices utilisent des techniques simples, mais demandent une certaine maîtrise, comme la présentation du théorème des probabilités totales de façon dynamique :
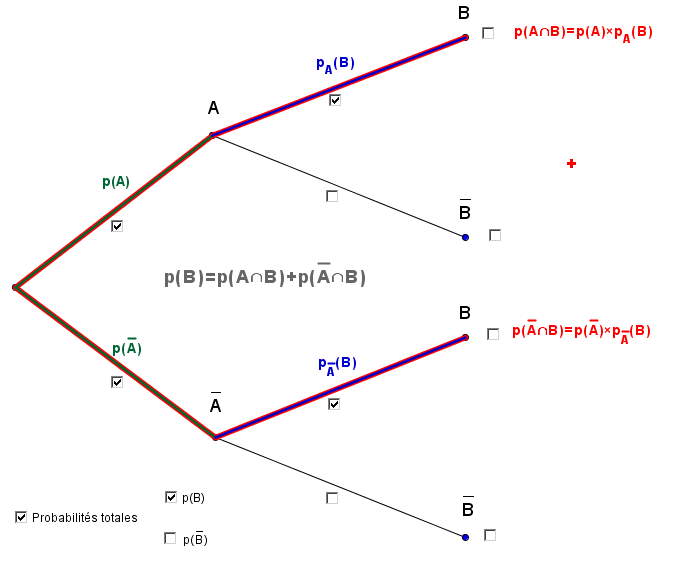
Une fois le logiciel « apprivoisé » coté enseignant, on peut laisser aller son imagination pour développer des animations diverses correspondant à sa façon d’enseigner, à ses besoins et ses envies, sérieuses ou plus ludiques : un spot lumineux, un jeu ou encore une modélisation.

La forte fréquentation du blog dès les premiers jours de sa création semble montrer l’existence réelle de ce besoin de formation. Je ne suis ni un expert, ni un spécialiste. Mon travail est simplement à l’image de ce que j’aurais aimé trouver pour faciliter mon apprentissage isolé et pour me faire gagner du temps. En espérant qu’il soit aussi utile pour la communauté.