Cet article continue la présentation de Xcas commencée dans les deux numéros précédents (voir 1,2 et 3), il propose deux autres TP qui avaient été présentés aux journées régionales 2006 de l’APMEP de Grenoble.
Deuxième partie : un TP en terminale S
Ce TP est le premier travail sur les aires en Terminale S.
Il a toutefois été préparé par une séance classique en classe entière(50 minutes) : chez eux, les élèves avaient tracé un arc de parabole d’équation y-x2 dans un repère orthonormé d’unité 10 cm, sur papier millimétré, pour x compris entre 0 et 1. En classe, souvent par équipe de 2, ils devaient proposer une évaluation de l’aire du domaine délimité par cet arc de parabole, les axes et la droite d’équation x = 1. Aucune indication supplémentaire n’a été fournie : une telle séance en classe, où chacun peut s ’exprimer, fait très vite émerger la question essentielle. Quelle précision ? On passe alors un peu de temps à parler de subdivision d’un intervalle et de l’intérêt ou non de choisir un pas constant.
Le logiciel Xcas, utilisé en salle informatique lors du TP proprement dit, en demi-groupe, va permettre d’automatiser des calculs, dont on a pu voir lors de la première séance qu’ils se révèlent assez vite complexes et fastidieux pour la majorité des élèves. Le travail préparatoire leur permettra d’entrer plus vite dans le vif du sujet et le graphique sur papier sera encore utilisé par certains, comme support au raisonnement. L’outil informatique permettra d’aller « voir de plus près » l’encadrement de l’aire demandé (et de modifier ensuite éventuellement les bornes du domaine ou la fonction).
L’avantage du logiciel Xcas, pour ce problème assez classique, est de travailler simultanément avec un tableur formel, une session traditionnelle de calcul algébrique avec des suites (simplification d’écriture, limites...) tout en gardant à l’esprit la finalité de l’exercice, à savoir calculer une aire.
Les valeurs obtenues sont exactes et les élèves se posent par exemple la question suivante : si on me demande un encadrement à 0,01 près, est-ce que je dois donner 10,51 et 10,52 ou bien 10,5143 et 10,5243 ?
On délègue à la machine des taches spécifiques, en prenant soin de bien les organiser, puisqu’on veut pouvoir les adapter et les réutiliser ultérieurement, ce qui ne va pas de soi pour tous les élèves ! Ceci n’interdit pas au professeur de demander des calculs « à la main », surtout lorsque les élèves ont vu que la machine fournit un résultat très simple. Ils se lancent alors plus volontiers et seuls dans le calcul, assurés que des simplifications ne manqueront pas d’apparaître.
TP Xcas : Calcul approché puis exact de l’aire située sous une parabole On a vu en classe comment estimer l’aire d’un domaine délimité par une courbe, l’axe des abscisses et deux droites verticales d’équations x=0 et x=1, en encadrant le domaine par des rectangles « un peu trop petits » puis « un peu trop grands ». Le travail est vite fastidieux si on doit le refaire pour augmenter la précision. On va utiliser un logiciel de calcul qui permet de confier les calculs à la machine et de garder ses forces pour réfléchir !!!
- Vous allez utiliser le logiciel Xcas qui permet de travailler dans pratiquement tous les domaines mathématiques, calcul algébrique, géométrie, étude de fonctions, résolution d’équations ou inéquations et programmation, plus le mode « tableur », mais il s’agit toujours faire du calcul formel.
Pour obtenir des expressions algébriques ou des valeurs numériques simplifiées, vous demanderez simplify(f(x)) ou evalf(f(5). Les commandes les plus courantes se trouvent dans les différents menus du bandeau supérieur. - Définition d’une fonction : tapez f(x) :=x^2, validez, puis F :=plot(f(x)) puis D :=droite(y=2x-1). La parabole et la droite apparaissent chacune dans une fenêtre graphique. Demandez f(5) puis puis f(x+1) puis f(sin(x)) + f(cos(x)). Contrôlez les résultats obtenus, en demandant « simplify » ou « evalf ».
Pour obtenir deux représentations graphiques dans le même repère, il faut donner les deux instructions dans la même ligne de commande, séparées par une virgule ou bien ouvrir une session de géométrie (Edit, Ajouter, Géométrie) dans laquelle on demandera F :=plot(f(x) puis, par exemple, couleur(D :=droite(y=2x-1),bleu). - Ouvrez une session tableur en allant dans edit puis ajouter puis tableur : vous pouvez donner un nom à ce tableau et changer le nombre de lignes et colonnes. Vous avez par défaut un tableau de 10 colonnes (de A à J) et 33 lignes (de 0 à 32). Vous pouvez changer ultérieurement en cliquant sur la ligne de message en haut du tableur. Vous pouvez utiliser les fonctions classiques d’un tableur, par exemple « =sum(A10:A25) » pour demander la somme des nombres contenus dans les cellules A10 à A25.
Dans le tableau, les calculs sont exacts, donc vous pouvez travailler avec des fractions : essayez A0=1/2, B0=1/3 et demandez en C0 « =A0+B0 ». Si vous voulez la valeur approchée, il faudra demander « =evalf(A0+B0) ». Si A0=x, B0=1/3, observez C0=A0+B0, puis vous demanderez dans D0 « =simplify(C0) ». Saisissez dans D1 l’expression f(D0) et observez le résultat obtenu. Proposez une instruction permettant d’obtenir l’écriture développée de D1 dans D2.
Attention, si vous utilisez des nombres décimaux, le séparateur entre la partie entière et la partie décimale est le point et les calculs seront alors automatiquement réalisés en mode approché. Par exemple la valeur 1/2 et la valeur 0.5 ne donneront pas les résultats des calculs sous la même forme.
Dernière remarque avant de se lancer : on sauvegarde son travail pour le tableur, comme pour les autres travaux. Les fichiers « .tab » et « .xws » correspondent respectivement à des tableurs ou des sessions complètes. -
Mise en place des calculs des rectangles : Dans la colonne A, on va indiquer les abscisses x et dans la colonne B les ordonnées y pour ensuite calculer les aires des rectangles inférieurs et supérieurs qui « encadrent » la parabole, pour des abscisses qui vont varier de 0 à 1 par pas constant égal à la valeur qu’on indiquera dans la cellule A0, on commence par exemple avec un pas égal à 1/10. Cette valeur pourra être modifiée et Xcas recalculera automatiquement.
- Dans la cellule A1 on indique la première valeur de x, donc 0, et dans A2, on écrit « =A1+ A$0 », puis on valide et de nouveau on se positionne sur A2 et on clique sur « remplir », « vers le bas ».
Quel est le contenu de la colonne A à partir de la ligne 1 ? -
Dans la cellule B1 on indique la première valeur de y, donc =f(A1), puis « remplir », « vers le bas ».
Que contient la colonne B ? - On veut calculer une valeur approchée de l’aire A délimitée par la parabole d’équation y=x2 et les droites d’équations x=0 , x=1 et y=0. Comment calculer l’aire d’un « rectangle inférieur » ?
- Comment calculer l’aire totale représentée par tous les rectangles inférieurs ? Quelle formule simplifiée écrire pour obtenir cette aire ? Ecrivez ce calcul en utilisant les noms des cellules du tableur. Adaptez le nombre de lignes au pas choisi dans la colonne A.
Demandez à Xcas ce calcul dans la cellule C0. Dans C1, demandez une valeur approchée de C0. Montrez que si le pas est égal à 1/n, cette aire est égale à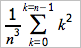 .
. - Mêmes questions pour les rectangles supérieurs. Vous inscrirez la formule de calcul dans la cellule D0 et sa valeur approchée dans D1. Quelle est la formule de l’aire supérieure pour un pas égal à 1/n ?
- Comparez les résultats numériques obtenus. Quelle est la précision de l’encadrement ? Calculez cette précision dans E0 et sa valeur approchée dans E1.
- Dans la session, demandez le calcul des aires en utilisant « sum(k^2,k,1,n)/n^3 », « sum(k^2,k,0,n-1)/n^3 », puis leur différence. Demandez une écriture simplifiée des calculs puis démontrez « à la main » les résultats obtenus.
- Modifiez les choix précédents pour affiner l’encadrement et obtenir une précision de 10- 2.
- Dans la cellule A1 on indique la première valeur de x, donc 0, et dans A2, on écrit « =A1+ A$0 », puis on valide et de nouveau on se positionne sur A2 et on clique sur « remplir », « vers le bas ».
- Comment doit-on modifier le travail précédent si on veut calculer une valeur approchée à 10- 2 près de l’aire comprise entre la parabole d’équation y =(x - 1)2 et l’axe des ordonnées ? Vous pouvez aller modifier la fonction f dans la session en écrivant f(x) :=(x - 1)2 (n’oubliez pas de valider) puis revenez à la feuille de calcul et observez les nouvelles valeurs. Expliquez ce qui se passe.
- Encadrez l’aire du domaine compris entre la parabole d’équation y=x2, la droite d’équation x=a et les axes du repère, en utilisant n subdivisions de l’intervalle [0 ; a]. Que se passe-t-il quand n augmente ? Quand n tend vers + ∞ ? Est-ce que vous pouvez en déduire la valeur exacte de cette aire en fonction de a ?
Ce TP va se poursuivre, peu de temps après, par un autre, du même type, mais la courbe sera alors celle de l’hyperbole d’équation y=1/x avec x compris entre 1 et 2, puis 1 et 4, 1 et 8 etc, dont le but sera alors de faire apparaître des relations entre les valeurs de ces aires.
La plupart des élèves veulent réutiliser, en la réaménageant un peu, leur feuille de calcul du TP précédent et sont alors confrontés à une aire supérieure qui est en fait une aire inférieure et vice versa... La connaissance du sens de variation de la fonction apparaît alors indispensable !
Le travail avec Xcas permet de voir très vite les effets d’une « petite erreur », de réfléchir puis de comprendre et modifier les formules, sans abandonner par lassitude, ce qui est hélas trop souvent le cas.
On essaie ici de faire sentir la nécessité d’observer des résultats, de conjecturer, pour bien comprendre le problème avant de commencer à démontrer.
Troisième partie : la tortue
La partie Tortue de xcas contient des commandes permettant de faire des dessins comme en Logo en donnant des ordres à une tortue possédant un crayon. Ces dessins sont faits dans l’écran graphique Tortue qui est obtenu avec le raccourci clavier : Alt+d.
La tortue est un curseur graphique représenté par un triangle : c’est un robot orienté qui peut avancer, reculer, tourner sur place à droite ou à gauche et tracer ses déplacements.
Contrairement à Logo il n’y a pas de commandes gérant des changements d’échelles mais il y a des commandes permettant de réaliser des cercles, des arcs de cercle, des figures pleines comme des disques, des rectangles pleins, des triangles pleins etc...
1-ière séance
On dessine un triangle rectangle isocèle plein avec comme position de départ et d’arrivée de la tortue, le milieu de l’hypoténuse avec un cap dirigé selon la hauteur. Il faut donc faire tourne_gauche après chaque efface.
tri(a) :={
triangle_plein(a,a) ;
tourne_droite ;
triangle_plein(a,a) ;
tourne_gauche ;
}
On dessine un sapin formé de 2 triangles tri de dimensions 50 et 40 pas de tortue et décalés de 40 pas de tortue, avec comme position de départ et d’arrivée de la tortue le milieu de l’hypoténuse avec un cap dirigé selon la hauteur de tri(50).

On écrit la procédure sapin0 :
sapin0() :={
tri(50) ;
avance(40) ;
tri(40) ;
recule(40) ;
}
2-ième séance
On demande d’écrire à partir de sapin une procédure paramétrée avec 2 paramètres a et b : a pour 50 et b pour 40. On écrit en classe en expliquant :
sapin(a,b) :={
tri(a) ;
avance(b) ;
tri(b) ;
recule(b) ;
}
On a donc fait dessiner la dernière fois sapin(50,40). On demande maintenant de dessiner les sapins de la famille du sapin(50,40), c’est à dire ceux qui ont la même forme que lui à un agrandissement ou à une réduction près. On demande aux enfants de remplir le tableau suivant :
a |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
b |
a |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
b |
40 |
a |
85 |
90 |
95 |
100 |
105 |
110 |
115 |
120 |
b |
Les enfants remplissent tous le tableau au début en se servant systématiquement de l’addition ils écrivent :
a |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
b |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
Mais lorsqu’ils testent sapin(20,10) ils n’obtiennent qu’un seul triangle et s’aperçoivent qu’il y a une erreur....et ils sont alors obligés de procéder par essais et erreurs ...mais cela est quelquefois difficile car il n’y a guere de différence entre sapin(45,35) et sapin(45,36). Il faut donc demander :
si a=100 que vaut b ? si a=10 que vaut b ? si a=20 que vaut b ?
si a=5 que vaut b ? si a=25 que vaut b ?
Comment écrire cette famille avec un seul paramètre ? On veut arriver à l’écriture de la procédure :
famille_sapin(k) :={
sapin(5*k,4*k) ;
}
Ainsi, sapin(50,40) est identique à famille_sapin(10).
3-ième séance On peut ensuite faire un dessin libre en demandant de dessiner une forêt de sapins, et ensuite faire dessiner une famille de n sapins en ribambelle, soit par ordre croissant, soit par ordre décroissant. On écrit par exemple :
sapins1(n) :={
pour k de 1 jusque n faire
famille_sapin(k) ;pas_de_cote(10*k) ;
fpour ;
} ;
sapins2(n) :={
pour k de n jusque 1 pas -1 faire
famille_sapin(k) ;pas_de_cote(10*k) ;
fpour ;
} ;
Question : combien faut-il mettre de pas de côté pour que les sapins se touchent seulement en un point avec ses voisins ?
On peut aussi écrire des procédures récursives comme par exemple : qui dessine aussi une famille de n sapins en ribambelle
sapinsr(k,n) :={
si n>0 et k>0 alors
famille_sapin(k) ;
pas_de_cote(10*k) ;
sapinsr(k-1,n-1) ;
fsi ;
}
Conclusion :
Nous n’avons présenté ici que certaines des possibilités d’utilisation de Xcas, d’une part pour ne pas dépasser le niveau du lycée (où on n’utilise qu’une très faible partie des fonctionnalités de Xcas en calcul formel, arithmétique, etc.), d’autre part parce que certaines fonctionnalités n’ont pas encore été testées en classe (en particulier la géométrie dans l’espace et les statistiques). Nous invitons tous les lecteurs intéressés à essayer Xcas et à nous faire part de leurs remarques sur le forum internet Xcas (depuis Xcas choisir le menu Aide->Internet->Forum ou saisir dans votre navigateur l’adresse http://pcm1.e.ujf-grenoble.fr/XCAS/).