par Patrice Debrabant
La machine de Turing est un modèle théorique « équivalent » à un ordinateur.
Un des intérêt de ce modèle est qu’il apparaît au sommet d’une hiérarchie de modèles plus simples, la Hiérarchie des automates.
 |
Dans cet article, on va s’intéresser aux automates finis.
 |
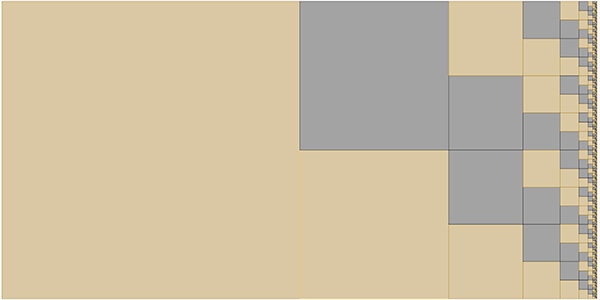NB : Cet article ne vise pas à donner une présentation académique des automates finis. Celle-ci pourra être trouvée dans d’autres sources. On rappellera juste certains résultats classiques importants, le fil directeur étant de présenter les notions sous un angle différent. Pour prendre une analogie, c’est un peu comme si l’on envisageait les fonctions à partir de leur représentation graphique plutôt qu’à partir de leur formule algébrique. Dans le domaine des automates, c’est une approche qui est rarement développée.
Pour une présentation classique en français du concept d’automate fini, on pourra consulter l’ouvrage classique (et indémodable) Langages Formels… d’Olivier Carton.
La présentation Wikipédia est plus ancrée dans la technologie, elle pourra être consultée en complément (et illustration).
Automates
Les automates sont des machines abstraites qui modélisent des mécanismes de « calcul ». Les automates que l’on va considérer (auxquels on va se limiter) auront les caractéristiques suivantes :
- ils prendront en entrée des mots finis sur un alphabet fini ;
- ils possèderont un nombre fini de configurations internes, appelées états ;
- ils disposeront éventuellement d’un système de mémoire ;
- ils évolueront selon un nombre fini de règles. Chaque règle décrira l’évolution de l’automate en fonction des symboles d’entrée, de l’état, et de la mémoire. Cette évolution pourra être déterministe ou non déterministe ;
- ils posséderont des configurations d’acceptation (et éventuellement de refus).
Définition d’un automate fini
Intuitivement, un automate fini est une machine qui peut prendre différents états.
Quand on soumet un mot à cette machine, celle-ci « lit » successivement les lettres du mot. A la lecture de chaque lettre, la machine peut changer d’état si la transition initiée par cette lettre est autorisée.
Certains états sont des états initiaux. Certains états sont des états finaux.
Si l’automate passe d’un état initial à un état final en lisant un mot, ce mot est « accepté » (ou reconnu).
Les changements d’état sont régis par des règles de transition : si l’automate est dans l’état x et lit la lettre y, il passe dans l’état z.
Un automate fini est représenté par un graphe orienté dont les arrêtes sont étiquetées. Les noeuds sont les états. Les états initiaux sont marquée par une flèche entrante, les états finaux sont marqués par un double cerclage.
Exemples :
L’automate ci-dessus lit des mots composés sur l’alphabet {a,b}.
Il a quatre états, dont un état initial ($q_1$) et un état final ($q_3$).
Il reconnaît les mots commençant par b et finissant par a.
Cet automate est déterministe.
L’automate ci-dessus lit des mots composés sur l’alphabet {a,b}.
Il a deux états, dont un état initial et un état final.
Il reconnaît les mots comportant au moins un a.
Cet automate est non déterministe : quand il est dans l’état $0$ et lit la lettre a, il peut rester dans l’état $0$ ou passer dans l’état $1$.
Les automates finis peuvent modéliser un grand nombre de mécanismes dans des domaines différents (électrotechnique, linguistique, biologie, logique,...) :
- fonctionnement de composants électroniques ;
- protocoles de communication ;
- phase initiale de compilation d’un programme informatique ;
- ...
Plus précisément, un automate A sur l’alphabet B est un quintuplet (Q,B,E,I,F) où Q est fini, I $\subseteq$ Q, F $\subseteq$ Q, E $\subseteq$ Q $\times$ B $\times$ Q. Q est l’ensemble des états, I celui des états initiaux, F celui des états finaux. E est l’ensemble des transitions.
Un chemin est une suite finie de transitions consécutives, que l’on peut noter $q_0 \xrightarrow{a_1} q_1 \xrightarrow{a_2} ... \xrightarrow{a_n} q_n$
Le mot $a_1 ... a_n$ est l’étiquette du chemin.
Langage L(A)
Un chemin est dit acceptant ou réussi lorsque son état de départ est initial et son état d’arrivée est final. Un mot est accepté ou reconnu par l’automate A s’il est l’étiquette d’un chemin acceptant de A.
Le langage des mots acceptés par l’automate A est noté L(A).
Automates déterministes et automates non déterministes
Un automate est déterministe s’il admet un seul état initial et une seule transition à partir d’un état donné étiquetée par une lettre donnée.
Propriété : tout langage reconnu par un automate fini non déterministe est également reconnu par un automate fini déterministe.
Démonstration : à partir de l’automate non déterministe A, on construit un automate Mega_A dont les états sont les parties de Q (plusieurs états de A), ces parties étant finales (en tant qu’état de Mega_A) si elles contiennent au moins un état final.
La transition $P \xrightarrow{a} ...$ où P est un état de Mega_A est $P \xrightarrow{a} P’$ où $P’= \{ q \ | \ \exists p \in P \ p \xrightarrow{a} q \}$
L’automate Mega_A est déterministe et reconnaît le même langage que A.
Automates finis et expressions rationnelles
Les langages qui peuvent être reconnus par un automate fini sont d’un type particulier.
Théorème de Kleene : Les langages reconnus par un automate fini sont les langages rationnels.
Un langage est dit rationnel s’il est égal à un expression rationnelle. Cette expression est construite à partir des opérandes élémentaires $\emptyset$, $\{\epsilon\}$, $\{a\}$ pour $a \in$ alphabet $B$, et des opérateurs union ($\cup$), concaténation ($.$), et étoile ($^\star$).
L’opérateur de concaténation $.$ est défini ainsi :
$A.B = \{ v.w \ | \ v \in A \quad et \quad w \in B \}$
L’opérateur unaire $^\star$ est défini
$A^\star = \{ v_1.v_2....v_k \ | \ k \geq 0 \quad et \quad \forall i \geq 0 \ v_i \in A \}$
Il y a un ordre de priorité pour ces trois opérateurs :
L’étoile est prioritaire sur la concaténation, elle-même prioritaire sur l’union.
Exemple : Soit $C = \{b\}$, $D = \{a\}$, $E = \{bb\}$ (on omet désormais le symbole de concaténation).
L’expression $CD^\star C \cup E^\star$ représente (est) le langage contenant les mots tels que :
- le mot commence et se termine par b et contient un nombre arbitraire de a mais pas de b entre eux, ou
- le mot contient un nombre pair de b et pas de a.
Ce langage peut s’écrire plus simplement, par abus de langage : $ba^\star b \cup (bb)^\star$
Alphabet à deux lettres et représentation graphique d’un automate
Si on utilise un alphabet à deux lettres, on peut obtenir une représentation graphique d’un automate, ou plus exactement du langage qu’il reconnaît (du problème qu’il résout).
 |
On a représenté ci-dessus les solutions d’un problème de décision d’entrée {a,b}$^*$.
La case la plus à gauche pour cet automate est blanche, ce qui indique que l’état initial n’est pas un état final, autrement dit que la chaîne vide n’est pas acceptée.
Dans la configuration initiale, on a un ruban dans la position suivante :
La colonne de gauche de la représentation graphique indique que (de bas en haut) :
la chaîne vide donne Faux.
a donne Faux.
b donne Vrai.
La colonne suivante indique que :
aa donne Faux.
ab donne Vrai.
ba donne Faux.
bb donne Vrai.
La suivante indique que :
aaa donne Faux
aab donne Faux
aba donne Faux
abb donne Vrai.
etc.
On pourrait proposer une définition théorique de cette représentation graphique en utilisant l’écriture binaire, mais on va considérer ici que la présentation naïve ci-dessus est suffisamment éloquente.
Exemples
1)
Le langage reconnu par l’automate contient les mots commençant par b et finissant par a.
 |
2)
Le langage reconnu par l’automate contient les mots ayant un nombre impair de lettres.
3)
Le langage reconnu par l’automate contient les mots tels que :
- si le mot commence par b, sa longueur doit être au moins deux ;
- si le mot commence par a, il doit continuer avec des b jusqu’à la fin.
4)
Le langage reconnu par l’automate contient les mots qui se terminent par ab.
5)
Le langage reconnu par l’automate contient les mots qui commencent et finissent par la même lettre.
6)
Le langage reconnu par l’automate contient les mots qui ne contiennent ni aa ni bb.
7)
Le langage reconnu par l’automate contient les mots ayant un nombre pair de b.
Cette représentation graphique peut être interprétée non seulement comme (l’équivalent de) la représentation graphique d’une fonction, mais aussi, pour un automate fini déterministe, comme l’évolution d’une « espèce d’automate cellulaire » [1] particulier, l’axe horizontal étant un axe des temps.
Reprenons par exemple l’automate de la figure 4).
Si on l’interprète comme l’évolution d’un « automate cellulaire », on peut l’expliciter ainsi :
Pour un automate non déterministe, chaque « cellule » peut être associée non pas à un état, mais à un ensemble d’états (tous les états atteints).
Variante multicolore
Pour un automate fini, si on associe une couleur différente à chaque état, on peut obtenir une représentation graphique multicolore du fonctionnement d’un automate fini sur les différentes entrées.
En voici un exemple (qui ne correspond pas à l’exemple précédent) :
Pour aller plus loin...
Cette représentation graphique d’un automate fini peut être généralisée à tout langage sur un alphabet binaire. En particulier, on peut l’appliquer au langage reconnu par une machine de Turing.
Les langages reconnus par une machine de Turing correspondent aux fonctions calculables. La question « comment reconnaître une fonction calculable ? » peut alors être transposée en géométrie : Quel type de surface obtenue comme représentation graphique d’un problème correspond à une fonction calculable ? [2]