Au quotidien, de nombreuses situations sont des situations de proportionnalité ou assimilées comme telles. Si l’on veut comprendre son environnement, il est impossible de se passer de la proportionnalité.
Introduction
Au quotidien, de nombreuses situations sont des situations de proportionnalité ou assimilées comme telles. Si l’on veut comprendre son environnement, il va être impossible de se passer de la proportionnalité. A l’école, la proportionnalité touche aussi à tout : dès le cycle 3, pendant lequel elle devient un sujet explicite dans les programmes, on la retrouve dans tous les domaines. Au cycle 4 et au lycée, ce sera encore plus vrai. A partir du collège, si on n’a pas compris la proportionnalité, si on n’est pas compétent dans les techniques de calcul de situations de proportionnalité, on est coincé. Mais pour y parvenir, c’est compliqué.
Cette complexité est due en particulier à ce qu’on travaille la proportionnalité bien avant d’avoir à sa disposition les outils nécessaires. Mais il n’est pas possible de procéder autrement : s’en priver éliminerait trop de notions, de savoirs, de supports pour développer des compétences, et ne permettrait pas de comprendre le monde de la même façon. Alors on assume que ce soit un casse-tête : modéliser la proportionnalité est en réalité impossible pendant des années, et on ne peut que l’illustrer. En exhibant des exemples et des contre-exemples, on va essayer de rendre les élèves compétents pour la reconnaître et l’utiliser.
S l’on veut aller plus loin et réfléchir à nos gestes professionnels, il va falloir avant tout s’interroger sur ce qu’est la proportionnalité. Cela nous mènera à une autre question : pourquoi la proportionnalité constitue-t-elle un thème central, en particulier au collège, mais forcément irrigué par un travail préalable à l’école ? Et puis dans les programmes, alors, du cycle 1 à la fin du cycle 4, à quoi cela ressemble-t-il ? Enfin, nous pourrons nous interroger sur des obstacles en lien avec la proportionnalité.
La proportionnalité, c’est quoi ?
Voilà une question difficile, pour commencer, mais inévitable. Dans les manuels de CM1 à la 5e, on trouve des « définitions » variées. En voici quelques exemples :
- « Proportionnalité : caractère des grandeurs proportionnelles entre elles », « Une situation est proportionnelle lorsqu’elle peut se résumer par un tableau de proportionnalité », « Des séries de nombres sont proportionnelles lorsqu’une augmente dans la même proportion que l’autre » : certes, mais définir la proportionnalité en s’appuyant sur la proportionnalité est un exercice de style qui ne peut rien apporter aux élèves ;
- « On parle de proportionnalité lorsque deux séries de nombres varient de la même façon » : voilà qui est faux. Lors d’un trajet en voiture à une vitesse non constante (ce qui est le cas « dans la vie »), la distance croît, le temps de trajet aussi. Mais ce n’est pas proportionnel ;
- « Quand on peut passer d’une série de nombres à une autre, en multipliant ou en divisant par un même nombre non nul, c’est une situation de proportionnalité » , ou bien « Pour résoudre un problème de proportionnalité, on peut utiliser la multiplication (ou la division) d’une quantité par un nombre, l’addition (ou la soustraction) de quantités, le passage par l’unité ou le coefficient de proportionnalité » : se rapporter à des techniques ne constitue en réalité pas une définition, et ne permet sans doute pas de comprendre le concept.
En réalité, il existe deux entrées pour définir la proportionnalité : la théorie des proportions, avec les fractions égales, et la théorie de la linéarité, avec les fonctions linéaires. La fonction linéaire permet de passer au continu (ce que ne permet pas explicitement la théorie des proportions et ses tableaux de proportionnalité, discrets), elle porte toutes les propriétés liées aux différentes techniques de calcul des situations proportionnelles, elle fait le lien avec les représentations graphiques.
Ces deux modèles ne sont évidemment pas incompatibles : ils permettent de modéliser différemment, et s’adaptent plus naturellement à telle ou telle situation. La fonction linéaire généralise, mais elle n’est pas accessible de façon précoce au niveau de l’école (il faut attendre la classe de troisième, nous allons en reparler), et ne fait malheureusement pas partie des savoirs partagés dans la population.
« Les deux modèles sont équivalents, ils décrivent les mêmes situations. (…) La théorie des proportions est adaptée au cadre discret (nombre fini de valeurs) et la linéarité est adaptée au cadre continu (nombre infini de valeurs). (…) Il y a clairement un saut épistémologique entre l’utilisation des propriétés additives et multiplicatives (addition/multiplication) et le retour à l’unité (division). Les deux conceptions théorie des proportions et linéarité ne sont pas antinomiques et sont même appelées à coexister lorsque les élèves ont le bagage mathématique suffisant pour faire vivre ces deux théories (c’est-à-dire lorsque les fractions sont aussi reconnues comme des divisions). »
Pourquoi la proportionnalité est-elle un thème d’étude crucial ?
C’est un sujet très intéressant, car il pourrait réconcilier différentes écoles pédagogiques : doit-on commencer par donner du sens, ou par les techniques ? Faut-il faire un choix binaire entre la construction de concepts et l’automatisation ? La proportionnalité illustre que non : les deux approches se complètent, aucune n’occulte l’autre. Nous faisons toutes et tous au mieux, en fait.
Un autre intérêt de la proportionnalité réside aussi dans cette difficulté : dans les nombres au cycle 3, apprentissages numériques, la proportionnalité est présentée comme un champ conceptuel. Elle est complexe, tentaculaire, construite petit à petit, très tôt en fait, avec des allers et retours constants entre la modélisation mathématique et la confrontation au réel. Elle est à l’interface du concret et de l’abstrait, fortement ancrée dans l’un comme dans l’autre. C’est ce qui la rend si difficile à enseigner vraiment, mais aussi si précieuse : elle permet d’autres approches, le développement de modes de pensée différents chez les élèves et les enseignants. En particulier, elle donne de belles occasions d’expliciter exemple vs. généralité, description vs. définition.
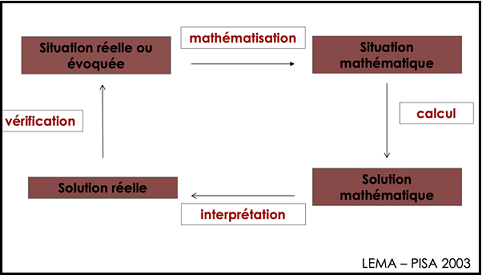
Un autre enjeu de la proportionnalité, c’est l’étude d’une situation, l’extraction de données, l’analyse, la capacité à passer de la situation concrète à sa mathématisation. On peut avoir compris ce qu’est la proportionnalité du point de vue du modèle mathématique, mais encore faut-il savoir regarder au bon endroit. Si je vous demande si cette situation est une situation de proportionnalité, qu’allez-vous me répondre :
« 4 pains au chocolat achetés, le cinquième offert »
Hé bien, ça dépend :
- Si on examine le nombre de pains au chocolat que je ramène à la maison et la somme dépensée, non, ce n’est pas proportionnel. En effet, les quatre premiers pains au chocolat ont chacun coûté le même prix, mais le cinquième n’a rien coûté. Le prix unitaire de chaque pain au chocolat n’est pas le même, pas de proportionnalité.
- Si maintenant je regarde le nombre de lots de 5 pains au chocolat et la somme dépensée, alors oui, il y a proportionnalité. Si j’achète n lots de 5 pains au chocolat, je paierai n fois plus qu’avec un seul lot.
Enseigner à analyser est fondamental pour donner des outils de pensée et rendre autonome. La proportionnalité en est une entrée.
La proportionnalité dans les programmes, ou la quadrature du cercle
Au cycle 2
Au cycle 2, toujours rien dans les programmes ; plus exactement, le mot « proportionnalité » n’apparaît pas encore. Mais, comme au cycle 1, les résolutions de problèmes tournent aussi autour de la proportionnalité, surtout à partir du moment où la multiplication est introduite, en CE1. Les problèmes portant sur des grandeurs et leurs mesures sont un terreau fertile pour cela, et les problèmes de partages ou de groupements aussi. On peut même déjà aborder des questions relatives aux échelles, sur des frises ou des plans.
Au cycle 3
Le cycle 3 marque l’arrivée de la proportionnalité de façon explicite. Elle est évoquée comme une « notion nouvelle ». Elle est liée à la compétence « modéliser » : il s’agit d’être capable de la reconnaître. Elle est présente dans tous les domaines : nombres et calculs, grandeurs et mesures et espace et géométrie. On la lit aussi dans les croisements entre enseignements.
Sur tout le cycle 3, l’attention est portée sur l’« identification à partir du sens de la situation » : on développe toute une gamme d’exemples pour que les élèves puissent s’appuyer sur la connaissance d’un répertoire et trouver leurs repères. En l’absence de définition, c’est le mieux que l’on puisse faire, même si cela risque d’être chargé d’un implicite délétère. En CM1, les attendus de fin d’année mentionnent la maîtrise de la linéarité additive et de la linéarité multiplicative, appliquées aux trois domaines des mathématiques scolaires de ce niveau. En CM2, on enrichit les techniques (passage à l’unité et coefficient de proportionnalité) et les applications (échelles et vitesses constantes, symbole % ). En sixième, les techniques sont synthétisées et automatisées, et les pourcentages, le lien avec les fractions, les questions d’échelles sont approfondies.
Au cycle 4
Au cycle 4, la proportionnalité est un outil cité dans les programmes de physique, chimie, sciences de la vie et de la Terre, technologie, géographie. Du côté des mathématiques, on la retrouve dans l’étude du ratio, des pourcentages, des agrandissements réductions et de transformations du plan, des fonctions, des vitesses, des calculs de fractions, du théorème de Thalès… On comprend bien en lisant cette liste que sans être déjà équipé solidement face à la proportionnalité, les difficultés vont s’accumuler. Il est attendu des élèves qu’ils sachent reconnaître des situations de proportionnalité variées, mais aussi qu’ils sachent sélectionner la technique la plus efficace et pertinente pour la résoudre. En quatrième, ce répertoire s’est enrichi d’interprétations graphiques et de la détermination d’une quatrième proportionnelle. Notons à cet égard que le fameux produit en croix n’est jamais cité, mais qu’un paragraphe sur les fractions présente l’égalité des produits en croix :
A partir de la classe de troisième, pour l’enseignant tout est cohérent et accessible, car les savoirs qui construisent la proportionnalité sont disponibles. En particulier, on dispose enfin des fonctions linéaires. La proportionnalité est cette fois vraiment modélisée, sans implicite, sans trucs et astuces, à supposer que l’accumulation de techniques n’ait pas occulté l’accès au sens pour les élèves.
Les obstacles
Conclusion
Il se joue bien des choses au travers de l’étude de la proportionnalité. D’une part nos élèves en auront besoin dans leur vie, pour décoder leur environnement et interagir avec lui. D’autre part les obstacles divers qui se présentent dans cette aventure en font un enjeu professionnel pour les enseignants et un enjeu intellectuel pour les élèves. Mais en plus de cela, l’étude de ce thème nécessite une réflexion collective, une progression, une programmation et une articulation des savoirs réfléchie en inter-niveaux, en inter-degré. C’est donc un objet à partager pour construire ensemble un parcours fluide des apprentissages.