La capacité de reproduire un algorithme par imitation fait partie de l’équipement de base de chaque enfant. Pour autant, la verbalisation d’un tel comportement n’est pas naturelle. C’est pourtant un préliminaire indispensable à la compréhension de ce qu’est un langage informatique, donc à l’acquisition d’une pensée informatique. Nous décrivons quelques expériences d’algorithmique débranchée en classe de CM2, dans lesquelles l’accent a été mis sur la verbalisation et la transmission.

Introduction

Dans un article précédent, nous avons distingué, dans l’apprentissage de la « pensée informatique » au sens de Pierre Tchounikine, plusieurs étapes. La première est le « comportement algorithmique », qui consiste à concevoir et exécuter un algorithme en vue d’atteindre un but défini. Qu’entend-on par là ? Le but conserve l’acception la plus large possible. Le chemin pour l’atteindre est décomposé en actions élémentaires, exécutées dans un ordre déterminé. Comme le montre Roland Maurer dans son cours de cognition comparée qui nous sert de référence générale, le comportement algorithmique n’est pas propre à l’espèce humaine. Les individus d’autres espèces exécutent des suites d’opérations d’un niveau de complexité tout à fait respectable. Cependant, lorsqu’on en vient à la question de la transmission de tels comportements, les humains ont un avantage certain : l’imitation intentionnelle. Elle consiste à percevoir l’intention du modèle, ce qui implique de reproduire chacun des détails menant à la réalisation de cette intention, puisque tous sont potentiellement utiles. Les éthologues l’opposent à l’émulation, plus courante chez les autres espèces, qui vise à reproduire un résultat sans nécessairement copier chacune des actions qui ont conduit à ce résultat.

La capacité d’imitation couvre chez l’humain, une grande partie des besoins de transmissions des algorithmes, quel que soit le domaine d’apprentissage. Pensez à l’acquisition d’une compétence manuelle : comment un maçon aprend-il à monter un mur, un menuisier à réaliser un assemblage ? Presque exclusivement par imitation. Pensez au succès des « tutos » sur youtube, comparés à des modes d’emploi rédigés. C’est vrai aussi en grande partie des apprentissages mathématiques : poser une addition, tracer un cercle… Le langage n’est pas toujours utile à l’élève, pourvu qu’on lui donne un modèle à reproduire. Pourtant, si l’objectif est de développer une pensée informatique, l’étape de verbalisation est cruciale : les élèves doivent prendre conscience de la nécessité d’un langage de communication. Mais utiliser un langage précis, exhaustif et non ambigu pour d’abord décrire un algorithme, ensuite le communiquer à une machine, est tout sauf évident pour un enfant.

Après avoir successivement examiné la question du langage sous l’angle de l’éthologie et de l’histoire des mathématiques, nous décrirons une progression expérimentale, réalisée par la première autrice dans sa classe de CM2. Nous avons mis l’accent sur l’algorithmique débranchée, de manière à favoriser la communication entre pairs, et à placer les élèves dans des cadres rassurants qu’ils connaissaient bien. Pour autant, les expériences menées, qu’il s’agisse pour l’élève de verbaliser son propre comportement, de transmettre à un camarade pour l’aider, ou aux élèves d’une autre classe dans le cadre d’un défi, ont mis en relief les difficultés de l’exercice.

Le lecteur complètera utilement ce qui suit, par la lecture de l’article d’Alain Busser et Patrice Debrabant dans la même revue. L’article de Thierry Dias donne d’autres pistes de réflexion. Yvan Monka a réalisé des expériences analogues aux nôtres, identifiant les mêmes difficultés. La fondation « La main à la pâte » a mis au point un tutoriel sur le même sujet.

Langage et enseignement

Si vous avez déjà assisté au travail d’un chien de berger en alpage, vous avez certainement été ébahi par la précision avec laquelle le berger guide son chien au sifflet, à des centaines de mètres de distance. Comment arrive-t-on à un tel degré de complicité ? Rien de plus simple, vous répondront les bergers. Quand leur chien commence à se faire vieux, ils prennent un chiot de quelques mois, et le laissent simplement suivre son aîné. Jour après jour, le petit apprend. Comment ? Non, ce n’est pas grâce aux explications de son mentor, qui a trop à faire pour cela ; c’est juste par émulation.

Pour autant, des situations d’enseignement intentionnel ont bien été observées chez les animaux. Les chattes apportent à leurs petits des souris mortes, puis des souris vivantes qu’elles maintiennent à portée des chatons. Les suricates enseignent à leurs petits à chasser les scorpions, d’abord en leur présentant des scorpions morts, puis des scorpions dont l’aiguillon a été ôté, avant de leur laisser affronter le danger. Pour autant, il ne semble pas qu’il y ait alors un langage de transmission. La seule émulation induit l’apprentissage. Les baleines à bosse ont développé une technique de chasse à base de rideaux de bulles, extrêmement sophistiquée. Comment est-elle transmise ? Dans la mesure où leur système d’échanges sonores est encore incomplètement compris, il est trop tôt pour affirmer ou infirmer qu’elles disposent d’un langage de transmission des comportements. Dans le cas des abeilles en revanche, pas de doute. Les danses qu’elles exécutent pour guider leurs congénères vers une source de nourriture constituent bien un langage, au sens algorithmique du terme.

Et les humains ? Force est de constater qu’une très grande partie des apprentissages utilise la capacité d’imitation, et pratiquement rien d’autre. Dans de nombreux cas, la part de l’échange verbal se limite essentiellement à « regarde comment je fais, puis fais pareil et répète, jusqu’à ce que tu aies compris ». Pas toujours pourtant. Voici un exemple. Du temps où les scratchs (aucune allusion à un langage bien connu) n’avaient pas encore envahi les tiroirs à chaussures de nos bambins, le laçage était un des apprentissages basiques de l’enfance. Comment était-il enseigné, et surtout comment était-il mémorisé ? Une recherche google vous mènera à plusieurs dizaines de pages et de vidéos, dans lesquelles il est souvent question d’arbres et d’oreilles de lapin. Il n’y a pas une histoire standard, pas plus qu’il n’existe d’algorithme canonique pour lacer ses chaussures. Si l’imitation suffit pour qu’un enfant réussisse un laçage correct au bout d’un ou deux essais, qu’il mémorise la procédure pour la répéter au quotidien est un autre problème. C’est là que le langage intervient de façon essentielle, comme support mnémotechnique. L’enfant associera les oreilles du lapin à une étape, l’arbre à une autre. En quelque sorte le déroulé de l’histoire l’aidera à mémoriser la succession des pas de l’algorithme. Mais en aucune façon ils n’en constituent une description, exhaustive et non ambigüe. Voici un exemple plus simple : le nœud de chaise, aussi appelé nœud de bouline en montagne. L’algorithme est assez standard, et l’histoire qui aide à sa mémorisation, connue de tous les utilisateurs.

Une boucle sur la corde : c’est le puits. Le brin libre est le serpent, le reste de la corde fait l’arbre. Le serpent sort du puits, fait le tour de l’arbre, et rentre dans le puits.

Si ce récit est suffisamment simple et frappant pour être utile à la mémorisation de l’algorithme, il n’est pas suffisant pour le décrire sans ambigüité. Nous allons voir maintenant comment le langage mathématique s’est graduellement affiné jusqu’à la spécification des algorithmes, et surtout comment il a participé à leur transmission.

Langage et mathématiques

Pour l’essentiel, le contenu de cette section relève de la « préhistoire de l’informatique » traitée plus en détail ailleurs.

Par son article de 1972, Donald Knuth avait magistralement démontré que les mathématiques mésopotamiennes étaient essentiellement constituées d’algorithmes. Certes, mais le langage était très elliptique et fort éloigné de notre manière d’écrire : voyez les traductions de Jens Høyrup dans « L’algèbre au temps de Babylone ». Les tablettes décrivaient de manière succinte les étapes vers la solution d’un problème numérique, en donnant quelques résultats intermédiaires. Il s’agissait donc toujours de « recettes de cuisine », c’est-à-dire d’algorithmes instanciés. Les auteurs avaient-ils extrait de leurs descriptions un algorithme théorique ? Rien ne permet de l’affirmer, et rien ne permet d’affirmer non plus qu’ils en aient vu la nécessité. Par exemple, les Mésopotamiens disposaient probablement déjà de l’algorithme d’approximation des racines carrées connu sous le nom de méthode de Héron. Mais il est peu probable qu’ils y aient vu autre chose qu’une recette. Voici cet algorithme en langage moderne. Soit A le nombre dont on veut approcher la racine.

Initialiser a
Répéter
……remplacer a par (A/a+a)/2
Jusqu’à atteindre la précision désirée

Il y a dans cette description, aussi imparfaite qu’elle soit encore, un saut conceptuel majeur : le remplacement d’une instance par une variable : « soit A le nombre… ». Il faudra de nombreux siècles pour que l’importance des variables soit comprise. La première description connue de l’algorithme ci-dessus est bien celle de Héron dans les « Métriques ». Pour lui, le carré A dont on doit calculer la racine est 720. Appréciez son énoncé, dans la traduction de B. Vitrac et F. Acerbi.

Puisque le carré le plus proche de 720 est 729 et qu’il a 27 comme côté, divise les 720 par le 27 ; il en résulte 26 et deux tiers ; ajoute les 27 : il en résulte 53 et deux tiers ; de ceux-ci, la moitié : il en résulte 26 1/2 1/3 : le côté de 720 sera donc 26 1/2 1/3 à très peu près.

Comme vous le constatez, Héron ne donne qu’un exemple de calcul, et seulement la première itération de l’algorithme. Même s’il devient clair dans la suite qu’on peut itérer pour améliorer la précision, ce n’est pas dit explicitement et bien sûr, aucun test d’arrêt n’est proposé.

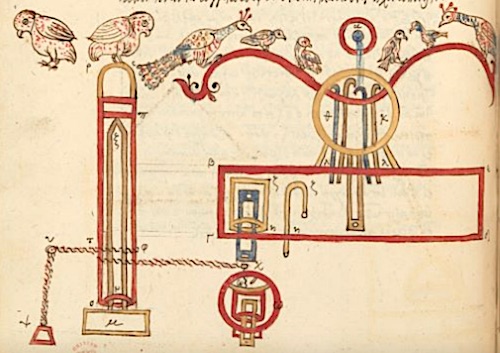
Puisqu’il est question de Héron, profitons-en pour évoquer ses magnifiques automates. Des mécanismes extrêmement ingénieux, permettaient de transformer la rotation d’un cylindre autour duquel était enroulé un cordon, en toutes sortes de tableaux animés. Difficile de ne pas voir dans la manière dont s’agençaient ces tableaux, de véritables programmes. Et les enroulements de cordons, les picots qui permettaient de changer de sens, ne constituaient-il pas un authentique langage de programmation ?

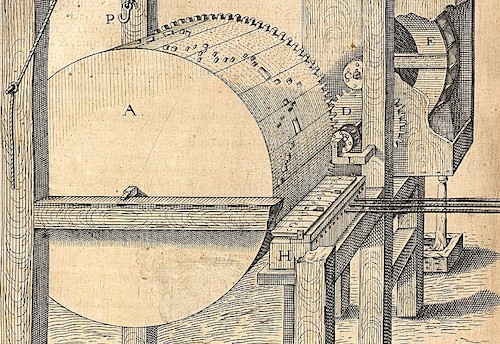Que dire du cylindre à picots ? Inventé par les Arabes du temps des frères Banu Musa, il a équipé entre autres les carillons d’église depuis la Renaissance, et toutes sortes d’automates, dont ceux de Vaucanson. Il est toujours en usage dans nos boîtes à musique. C’était bien une mémoire binaire, non ? Une variante, la carte perforée, avait été inventée à Lyon où elle équipait les métiers à tisser. En 1840, Babbage avait acheté un portrait de Jacquard, tissé en soie grâce à 24000 cartes perforées. De retour à Londres, il l’avait exposé dans son salon et ne manquait pas une occasion d’expliquer l’analogie avec sa machine analytique.

Certes, les automates de Héron, ceux de Vaucanson et le métier à tisser de Jacquard font partie intégrante de l’histoire de l’informatique, au même titre que les machines de Babbage. Mais les termes de programme, langage, mémoire, que nous avons employés à leur propos, sont parfaitement anachroniques. Nous projetons sur ces inventions du passé lointain, des catégories de pensée nées du développement récent de l’informatique. Revenons donc à une algorithmique plus classique.

Toujours d’après Donald Knuth, « le plus ancien algorithme non-trivial qui ait survécu jusqu’à aujourd’hui » est l’algorithme d’Euclide. Son premier énoncé se situe au début du livre VII des Éléments.

Deux nombres inégaux étant proposés, le plus petit étant toujours retranché du plus grand, si le reste ne mesure celui qui est avant lui que lorsque l’on a pris l’unité, les nombres proposés seront premiers entre eux.

Difficile d’y reconnaître un algorithme, sans exemple d’exécution, n’est-ce pas ? Puisque nous en sommes à Euclide, ses constructions géométriques sont autant d’algorithmes, à exécuter à la règle et au compas. À commencer par la toute première proposition du livre I : « sur un segment donné, construire un triangle équilatéral ». Voici la construction d’Euclide. Elle est accompagnée à droite d’une figure en couleurs sur laquelle nous allons revenir.

Du centre A et de l’intervalle AB, décrivons la circonférence BCD et de plus, du centre B et de l’intervalle BA, décrivons la circonférence ACE et du point C, où les circonférences se coupent mutuellement, conduisons aux points A, B les droites CA, CB.

Pendant des siècles, les élèves qui étudiaient les Éléments, s’entraînaient à reproduire les figures, à partir de descriptions comme ci-dessus. C’est donc que la spécification devait être suffisante, au moins si elle était accompagnée d’une figure déjà tracée. L’image de droite vient d’une édition de 1847 dans laquelle Oliver Byrne a remplacé les mots du langage d’Euclide par des pictogrammes colorés. Sa justification tient dans une citation tirée de l’Art poétique d’Horace : « notre esprit est moins vivement frappé de ce qui passe par l’oreille, que de ce qui s’offre aux yeux ». Il s’agit ici d’une substitution de langage, dont Byrne, dans son enthousiasme prosélyte, prétend qu’elle divise par trois le temps d’acquisition des Éléments d’Euclide. Voici maintenant la proposition 15 du livre IV : « Inscrire dans un cercle donné un hexagone équilatéral et équiangle ».

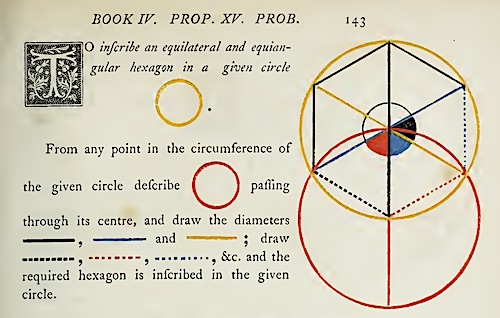Soit ABCDEZ le cercle donné . Menons le diamètre AD du cercle ABCDEZ, prenons le centre H de ce cercle, du centre D et de l’intervalle DH décrivons le cercle EHCT, joignons les droites EH, CH, prolongeons-les vers les points B, Z, et joignons AB, BC, CD, DE, EZ, ZA.

Sans la figure qui accompagne le déluge de lettres de la description, il y a peu de chances qu’un élève réussisse à comprendre l’algorithme. Avec la figure, la description n’est plus indispensable : Byrne n’avait pas complètement tort. Voici maintenant trois algorithmes de tracé d’un hexagone inscrit dans un cercle donné, écrits en langage naturel, sans lettres et sans figure.

Algo 1
Prendre pour écartement du compas le rayon du cercle
Placer la pointe du compas sur le cercle
Marquer avec la mine un des points atteints par le compas sur le cercle.
Itérer 5 fois :
……Placer la pointe du compas sur le dernier point atteint par la mine
……Marquer avec la mine le point du cercle non encore atteint
fin Itérer
Joindre par des segments les couples de points consécutifs atteints par la mine.

Algo 2
Prendre pour écartement du compas le rayon du cercle
Placer la pointe du compas sur le cercle
Tracer un second cercle
Tracer les trois diamètres du premier cercle, passant par son centre et :
……le centre du second cercle
……les deux points d’intersection des deux cercles
Joindre par des segments les couples de points consécutifs, parmi les extrémités des trois diamètres.

Algo 3
Prendre pour écartement du compas le rayon du cercle
Tracer un diamètre du cercle
Pour chacune des deux extrémités de ce diamètre :
……placer la pointe du compas sur cette extrémité
……marquer avec la mine du compas les deux points qu’elle atteint sur le cercle
fin Pour
Joindre par des segments les couples de points consécutifs, parmi les extrémités du diamètre et les quatre points atteints par la mine.

Nous laisserons les lecteur.trices trouver lequel des trois algorithmes est celui d’Euclide, et surtout se demander avec lequel des trois il serait le plus facile à quelqu’un n’ayant jamais vu la construction, d’obtenir un hexagone régulier. Question subsidiaire : lequel des trois algorithmes a le plus de chances d’être fidèlement mémorisé ? Nous reviendrons sur la verbalisation des figures géométriques dans la section suivante.

Quand les recettes de cuisine ont-elles commencé à ressembler à des algorithmes ? Ou en d’autres termes, quand les variables ont-elles remplacé les instances ? Cela a eu lieu après, et semble-t-il en liaison avec le développement de l’algèbre symbolique, à partir de Viète. Une étape importante pourrait avoir été la parution des Problèmes plaisans et délectables de Bachet de Méziriac, dans leur seconde édition de 1624. Nous sommes entre l’Art Analytique de Viète (1591), et la Géométrie de Descartes (1637). Sous couvert d’amusements, Bachet traite de questions arithmétiques difficiles, comme par exemple sa Proposition XVIII : « Deux nombres premiers entre eux étant donnés, trouver le plus petit multiple de chacun d’eux, qui surpasse de l’unité un multiple de l’autre ». Vous avez reconnu l’identité de Bézout, connue d’al-Haytham six siècles auparavant, mais que Bachet est le premier à avoir redécouverte en Europe… longtemps avant Bézout.

« Le plus petit multiple de chacun d’eux » se trouve par un algorithme que l’on peut voir comme une variante de l’algorithme d’Euclide, évoqué plus haut. Comment Bachet procède-t-il ? Il mélange la description verbale de l’algorithme sur des variables littérales, avec sa justification. Mais tout de même, comme il a pitié du lecteur, il donne, dans l’encadré en haut à gauche, une affectation de toutes les variables.

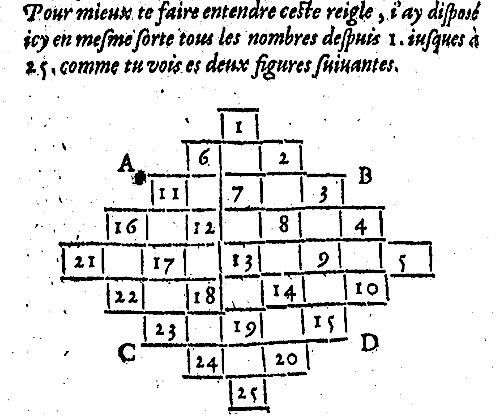Bachet utilise partout où c’est possible, cet artifice des encadrés contenant des exemples d’affectation. Mais quand il s’agit de décrire son algorithme pour construire les carrés magiques d’ordre impair, il renonce : il se contente d’un exemple, qu’il accompagne de façon quelque peu cavalière par : « Pour mieux te faire entendre cette règle, j’ai disposé ici en même sorte tous les nombres depuis 1 jusqu’à 25, comme tu vois sur les deux figures suivantes ». Autant dire que l’écriture rigoureuse de l’algorithme, n’était pas la préoccupation première.

Bachet et ses successeurs n’ont pas envisagé pas d’abandonner l’instanciation dans l’apprentissage d’un algorithme. L’examen des manuels anciens montre que leurs auteurs privilégiaient toujours l’aspect pédagogique. Un des plus célèbres est le cours d’algèbre d’Euler (1774). Au début du Tome 2, Euler traite des identités de Bézout. Il commence par une dizaine d’exemples non seulement instanciés, mais scénarisés dans des situations concrètes. Alors, et alors seulement, il passe à la description de l’algorithme, pour lequel il propose une présentation graphique. Ensuite, celui-ci est décrit avec des variables générales, pour aussitôt après, passer à un dernier exemple d’instanciation. Le tout prend une vingtaine de pages.

Que conclure de tout ceci ? Rien d’autre qu’une évidence : transmettre un algorithme à un humain pour qu’il l’exécute et le retienne, n’est pas la même chose que le transmettre à une machine. Développer la « pensée informatique » des enfants suppose qu’ils admettent la nécessité d’un langage pour s’adresser à l’ordinateur. Nous pensons qu’il est utile de leur faire comprendre auparavant la nécessité d’un langage précis pour transmettre un algorithme à un humain. Quelques expériences que nous avons réalisées dans cette direction, sont décrites dans la section suivante.

Verbaliser en classe

Plusieurs activités, au cours de diverses séquences d’apprentissages, ont été proposées aux élèves avec, pour intention pédagogique, un fil conducteur : faire apparaître pour les enfants l’importance de la communication dans la transmission d’instructions. Parmi les objectifs : se confronter aux difficultés d’interprétation du langage naturel pour comprendre la nécessité d’un autre langage et les amener vers celui du codage et de la programmation.
Dans le domaine 1 des objectifs du socle commun de connaissances, « les langages pour penser et communiquer », il est écrit :

« L’élève sait que des langages informatiques sont utilisés pour programmer des outils numériques et réaliser des traitements automatiques de données. Il connaît les principes de base de l’algorithmique et de la conception des programmes informatiques. Il les met en œuvre pour créer des applications simples. »

Une chose est de le savoir, une autre est de le comprendre. Comment amener les élèves à comprendre l’utilité d’un langage qui ne leur est pas naturel ? Si les enfants ont bien sûr entendu parler d’algorithmes en informatique, ils ne savent pas qu’il en existe partout ailleurs, et des plus simples : la routine du matin, le laçage de leurs chaussures, la multiplication à poser. Mais en quoi comprendre la relation de l’un à l’autre peut-elle être utile à nos élèves ?
Ce n’est pas pour rien si cette compétence figure dans « les langages pour penser et communiquer ». Il convient sans doute de s’arrêter sur l’intitulé : « un langage pour penser », et pas seulement en informatique, ni même en mathématiques, mais pour penser tout court. « Un langage pour communiquer », et pas seulement en informatique ni en mathématiques non plus, mais un langage parmi les autres, qu’il convient de maîtriser tout aussi bien. Dans les objectifs du socle, le langage mathématique est rangé juste après la langue et juste avant les langages des arts et du corps. C’est un langage bien particulier, mais un seulement parmi d’autres « langages spécifiques qui permettent de comprendre le monde » (comme le stipulent les programmes scolaires du cycle 4), des langages qui peuvent s’éclairer les uns les autres.

Aussi, au cours des différentes activités proposées pour accéder au langage informatique, les élèves sont-ils passés par celui du corps (manipulation et expérimentation sensible) et de l’oral (pour s’exprimer et communiquer) : des langages qui leur sont plus naturels et spontanés.

Parmi les activités réalisées en classe, nous avons évoqué dans un autre article les « dessins sur le sable », grâce auxquels nous avons pu aussi avancer vers une verbalisation algorithmique. Nous choisissons ici d’autres exemples pour illustrer une progression en trois étapes : l’exécution individuelle d’un algorithme dicté, l’élaboration et la transmission d’un algorithme entre pairs, le passage au langage informatique.

Dictées de figures : décodage d’instructions

L’activité est proposée sur le site Positivitea. Elle y est présentée comme un jeu d’écoute. Elle a été utilisée dans le cadre de la réflexion sur la verbalisation des algorithmes et la transmission de procédures. Les compétences sont listées dans les programmes scolaires des cycles 2 et 3 : « coder et décoder pour prévoir, représenter et réaliser des déplacements sur un quadrillage », « réaliser un programme de construction ». Toutefois, l’interdisciplinarité est évidente : on travaille par la même occasion le langage, la compréhension et la concentration. Dans ce premier exemple, c’est l’enseignante qui donne les consignes oralement, l’une après l’autre, et les élèves exécutent simplement les opérations décrites, selon les modalités d’une dictée. Les enfants n’ayant pas connaissance du résultat à obtenir, la motivation est suscitée par le résultat du tracé qu’ils découvrent à mesure des instructions. Aussi est-elle soutenue jusqu’au bout.

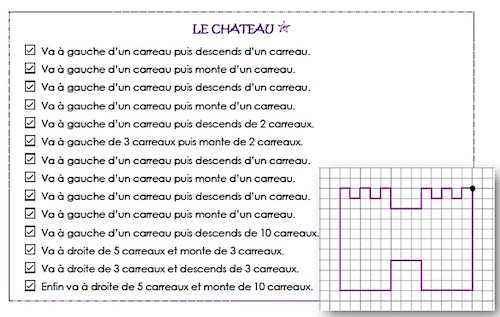L’attention est portée sur le lexique utilisé. L’objectif est de montrer aux élèves qu’un programme de construction peut être fragmenté en tâches simples facilement descriptibles et transmissibles, avec un vocabulaire et un répertoire d’instructions limité.
Dans un deuxième temps, ce sont les élèves qui pourront créer leur figure et écrire le programme de construction correspondant pour défier leurs camarades et leur en faire la dictée. Cette activité leur permettra de mettre en pratique la décomposition des différentes opérations à réaliser, de les verbaliser et de vérifier leur validité par l’adéquation de la figure obtenue avec le résultat espéré : l’évaluation est alors immédiate.

Ainsi, les élèves auront travaillé les deux compétences : décodage, codage. C’est ainsi que le rapport Villani-Torossian présente le travail sur les algorithmes : « on part d’un problème, on le modélise, on propose un algorithme, on l’exécute, on analyse le résultat : on part du concret, on passe par l’abstraction, et on retourne au concret ».

La collaboration entre pairs : des instructions pour communiquer

Dans le même rapport, il est écrit que « la verbalisation est centrale : dès la maternelle, le professeur encourage l’élève à raisonner à voix haute et à échanger avec les autres en mettant un haut-parleur sur sa pensée ».
En classe, le travail de géométrie est organisé de manière collaborative, en favorisant la formulation d’hypothèses de constructions pour la reproduction de figures proposées. L’entraide entre pairs est encouragée. Les élèves sont autorisés à se déplacer et à se parler.

Évidemment, il est admis par tous comme règle commune qu’aider, ce n’est pas « faire à la place », mais « expliquer » par des mots, ce qu’il faut faire. C’est l’intérêt de la chose dans le cadre de la verbalisation d’algorithmes : nous ne sommes plus dans l’imitation (reproduire ce qu’on nous montre) mais dans la réalisation d’instructions données. Celui qui aide est amené à décomposer les différentes étapes du tracé pour donner à son camarade des consignes simples facilement compréhensibles et réalisables malgré les difficultés. La verbalisation est directement liée à la manipulation : l’élève aidant s’appuie sur ce qu’il a déjà fait, verbalise comment il a fait (abstraction et codage) pour le transmettre, et l’élève aidé revient au concret et à la manipulation (concret et décodage).

Les enfants se rendent rapidement compte qu’aider, même si c’est valorisant, n’est pas facile. Cela demande de multiples compétences dans différents domaines : savoir s’exprimer de manière précise et compréhensible, s’adapter à son interlocuteur, savoir reformuler si nécessaire, manipuler un vocabulaire technique approprié notamment en ce qui concerne les termes géométriques, être capable d’analyser sa propre production pour la décomposer en une succession d’instructions. Et puis, cet exercice nécessite aussi des compétences transversales de relation à l’autre : être attentif à ce que l’autre ne comprend pas… et être patient.

En y réfléchissant, nous ne faisons pas autre chose avec nos élèves : décomposer des tâches complexes en tâches simples qu’il convient de leur expliquer clairement pour qu’ils se trouvent en position de réussite.

L’entraide entre pairs n’est pas la seule occasion de travailler la verbalisation des algorithmes géométriques en classe. Le travail collaboratif en est une autre. Tracer une rosace géante par équipes de cinq, c’est autre chose que de la tracer, seul, sur sa feuille de papier. Il faut s’organiser, réfléchir aux différentes étapes, nommer précisément ce qui est à faire et se répartir les tâches. Là encore, il faut non seulement « brancher son cerveau sur haut-parleur », mais être à l’écoute et inscrire le déroulé des différentes actions dans le temps.

Pour se faire comprendre des autres, il faut être attentif à son expression et être précis dans le choix de sa formulation. Lors de cette activité, tous les groupes n’y ont pas réussi : certains ne sont pas parvenus à réaliser la rosace, faute d’une communication efficace.

Le laçage des scoubidous : formaliser des instructions

Lors de la semaine des maths, une autre situation de verbalisation a été suscitée autour du laçage de scoubidous. Certains élèves savaient comment faire, d’autres non. Un travail par binôme a été mis en place : l’élève qui avait le savoir-faire avait pour consigne d’expliquer à son camarade la procédure, mais sans lui montrer, « uniquement avec des mots ».
L’observation de l’atelier a révélé que l’exercice était très complexe comme le montre cette vidéo.

La prise de repères est difficile. De quel fil parle-t-on ? Dans quel sens va-t-on ? Les enfants se rendent compte que « en haut », « en bas », « à gauche », « à droite », « dessus », « dessous », ont un sens très relatif selon le côté du scoubidou où ils se trouvent… Il faut donc réfléchir, se mettre à la place de l’autre, reformuler, trouver des repères et des termes plus précis et mieux adaptés. Pendant plusieurs séances, y compris avec des enfants plus jeunes de l’étude, les élèves se sont exercés à clarifier leurs instructions.

La plupart du temps, les instructions que l’on peut trouver sur internet sont essentiellement constituées de vidéos, de photos ou de dessins destinés à montrer comment faire. Un petit groupe d’élèves est parvenu à rédiger un « mode d’emploi du scoubidou », avec interdiction de dessiner ou de représenter les scoubidous, toujours « uniquement avec des mots ». Cet exercice a constitué un premier pas vers une verbalisation écrite des instructions.

Démarrage

Prends deux fils de scoubidou de deux couleurs différentes.

Prends les deux fils l’un contre l’autre.

Attrape leurs deux extrémités, joins-les.

De l’autre côté, tu trouves le milieu des fils : fais un nœud pour former une boucle.

Répéter :

Tiens le nœud et la boucle par en bas.

Au-dessus, il y a 4 fils :
dispose les en croix en alternant les deux couleurs.

Nomme les fils, en partant du haut et en tournant vers la droite : fil 1, fil 2, fil 3, fil 4.

Prends le fil 3, forme une boucle en le rabattant entre le fil 1 et le fil 4 : tu obtiens la boucle 1.

Prends le fil 1, forme une boucle en le rabattant entre le fil 2 et le fil 3 : tu obtiens la boucle 2.

Passe le fil 2 à l’intérieur de la boucle 1.

Passe le fil 4 à l’intérieur de la boucle 2.

Attrape les 2 fils à droite, les 2 fils à gauche, tire jusqu’à obtenir un carré.

Recommence.

Reste l’étape du décodage, qui n’a pas été testée, mais il y a fort à parier que l’exercice de lecture et de laçage à partir du texte n’est pas une mince affaire non plus.

L’entraide et la collaboration sont deux modalités de travail que l’on peut inscrire dans le fonctionnement de sa classe, et quel que soit le domaine d’apprentissage. Un autre type de transmission peut être mis en place en obligeant les élèves à se mettre en situation de communication.

Le défi entre classes : à l’épreuve de l’autre

Un travail a été entrepris dans deux classes de CM2 dans le cadre des formations en « constellations » prévues dans le plan Maths. Les élèves d’une première classe ont entrepris d’étudier le terrain de sport situé dans la cour, pour en tracer le plan et rédiger le programme de construction correspondant afin de le soumettre à la seconde classe. Les élèves de la seconde parviendraient-ils à identifier le terrain de sport ?

Il fallait tout d’abord prendre des mesures sur le terrain. Il s’agissait ensuite d’élaborer un tracé à main levée pour reporter les mesures prises sur place. Les élèves doivent maintenant communiquer sur les tracés à reproduire : ils réfléchissent déjà à la mise en mots du futur programme de construction en posant le lexique adapté sur les formes qu’ils ont observées.

Le dessin à main levée a été retravaillé collectivement en observant les formes composant la figure, en définissant et en manipulant les termes techniques qui devront être réinvestis lors des séances suivantes. Les mesures ont été vérifiées et adaptées pour pouvoir tracer une figure à l’échelle, à l’aide des instruments géométriques. Les élèves ont rédigé le programme de construction correspondant, destiné à leurs camarades de l’autre classe. Ce travail a été fait par petits groupes, afin de permettre aux élèves de discuter des instructions à donner et de verbaliser entre eux.

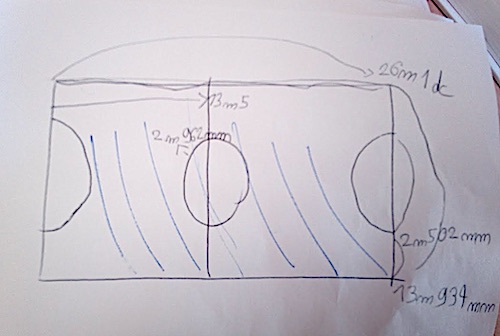C’est l’étape du travail qui nous intéresse le plus ici : pour pouvoir concevoir le programme de construction, les élèves ont dû s’approprier les éléments de la figure en les mesurant, en les observant, en les nommant. C’est-à-dire que pour parvenir à abstraire suffisamment pour isoler les tâches les unes des autres et pour les décrire dans l’ordre chronologique, il faut qu’ils aient eux-mêmes expérimenté la construction.

En travaux d’équipe, ce travail a demandé de la réflexion, suscité des débats, des désaccords et des reformulations pour parvenir à une proposition qui semble convenable aux enfants, comme par exemple dans cette vidéo.
Les premiers essais font état de difficultés évidentes, non seulement en expression écrite, mais aussi dans la maîtrise du vocabulaire et des codages géométriques :

Une mise en commun a été faite, suite à laquelle des corrections ont été apportées pour obtenir une version définitive estimée compréhensible par les élèves.

Les programmes de construction ainsi rédigés, ont été transmis sous forme de défi aux élèves de l’autre classe : « saurez-vous tracer la figure et reconnaître de quoi il s’agit ? ».

Les productions des élèves défiés ont été, dans une grande majorité, à la mesure de la difficulté de l’exercice : fort décevantes pour les élèves rédacteurs. Les élèves défiés ont pu faire une critique des programmes qui leur étaient proposés : imprécision du vocabulaire, étapes manquantes ou dans un ordre inapproprié, mesures oubliées… et les élèves rédacteurs ont pu se rendre compte de l’exigence dans la précision des instructions à donner pour obtenir le résultat escompté. Ils ont réalisé qu’il fallait donner des repères, « nommer les points » et indiquer où les placer, détailler précisément les étapes, « être plus précis et plus clair » sur les mots et les mesures, « mieux choisir le vocabulaire ». Les figures les plus réussies sont celles qui répondent à un programme constitué d’un enchaînement d’étapes bien clair, voire numéroté. Le vocabulaire géométrique y est suffisamment précis (segment, extrémité, point, perpendiculaire..), les figures y sont nommées (rectangle, cercle, demi-cercle) et des repères sont donnés (les points sont nommés).

Les programmes échoués l’ont été soit parce qu’ils étaient trop imprécis, soit parce qu’il manquait trop d’informations pour que leurs manques soient compensés. Par exemple :

• Il manque le rayon du cercle, voire l’étape nécessaire à son tracé en totalité.
• Les points ne sont pas nommés « fais un point sur les deux milieux des segments » (quels segments ?)
• La phrase est trop longue, les consignes multiples et mal explicitées : « prends le milieu (de quoi ?) et fais un point d’un des deux segments de 14 cm (où ?) et trace sur le point (lequel ?) un demi-cercle vers l’intérieur (de quoi ?) de 4,5 cm de rayon. »

Certains élèves ont commenté et annoté le programme dont ils disposaient : « qu’est-ce qui mesure quoi ? », « incompréhensible », « il faut relier ? », « quel est le nom du point ? », « où est le centre ? », « quel angle ? », « Il manque le nom des points, le programme est incompréhensible ».

En ce qui concerne la verbalisation d’algorithmes, nous en sommes à la description des tâches en langage « naturel », c’est-à-dire dans la langue commune, celle qui nous sert à communiquer tous les jours, nous accédons tout juste au langage mathématique avec ses termes techniques. Nous sommes encore loin d’un langage codé.

Du langage naturel au langage codé : les spirolatères

L’activité suivante était, dans un premier temps, destinée à réinvestir la notion d’angle droit.

Les élèves ont d’abord formé des spirolatères avec des allumettes. Ils ont vite observé le caractère répétitif des instructions : pose une allumette, tourne à droite, place une allumette de plus, tourne à droite, place une allumette de plus, etc. Nous avons défini cette succession d’instructions comme « un algorithme ».

Ils ont ensuite dû, par équipes, tracer des spirolatères en grand format dans la cour ; cela les a obligés à reformuler l’algorithme et adapter les mesures tout en le respectant.

À l’étape suivante, le spirolatère a été tracé sur papier quadrillé. Il a été réfléchi collectivement à la manière de verbaliser le tracé le plus précisément possible en se rappelant que quelqu’un d’autre devrait être capable de le reproduire, comme lors du défi entre classes.

Chaque élève a d’abord cherché à décrire les instructions sur son ardoise. Plusieurs programmes communs ont ensuite été élaborés. Par exemple :

Place un point au milieu

descends de 1

tourne à gauche de 2

monte de 3

tourne à droite de 4

descends de 5

tourne à gauche de 6

« Continue en ajoutant 1 à chaque fois »

Nous avons déterminé que le plus facile à comprendre était celui qui contenait le moins d’informations différentes possibles, qui donnait des repères et des mesures précises, et nous avons isolé l’instruction « continue comme ça » ou « à l’infini » qui permet d’itérer l’algorithme.

Les élèves étaient prêts pour une démonstration grandeur nature de la nécessité d’adopter un langage précis pour orienter des déplacements.

Langage et déplacement : les yeux bandés

L’activité suivante est inspirée du « jeu de langage de programmation ». Les élèves ont travaillé par binômes. L’un avait les yeux bandés et devait récupérer des objets dans la cour, l’autre devait le guider pour y parvenir, uniquement par la voix, comme dans cette vidéo.

Les élèves ont vite compris qu’il fallait réinvestir les caractéristiques définies précédemment : précision des instructions, orientations et mesures - ce qui a donné des programmes comme « Avance de x pas, tourne à droite / tourne à 90° vers la droite, avance de x pas, attrape. »

Du langage codé à l’ordinateur : Geotortue et Scratch

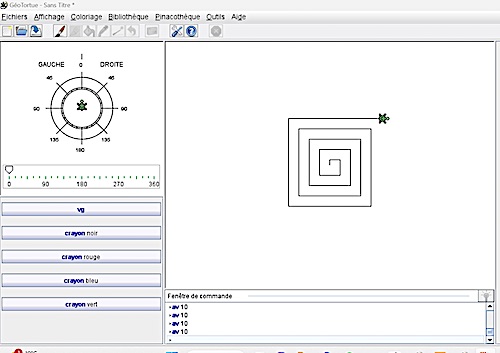La première activité sur ordinateur a été menée sur le logiciel Géotortue, choisi pour la simplicité des instructions et leur proximité avec celles déjà rencontrées. Les enfants ont vite compris à quoi correspondent les différentes commandes et sont parvenus rapidement à diriger la tortue pour tracer le désormais bien connu spirolatère. Le logiciel a été mis à disposition sur l’ordinateur de la classe, ce qui a permis aux élèves de le manipuler librement et de s’approprier les différentes commandes, transformant la figure, changeant sa couleur, etc.

Enfin, pour la dernière activité, les élèves ont pu manipuler le logiciel Scratch. Ils ont retrouvé des commandes familières, avec un éventail élargi, et notamment l’instruction « répète ». En autonomie sur l’ordinateur de la classe, ils sont aisément parvenus à tracer de nouveau le spirolatère, mais aussi à utiliser d’autres fonctions du logiciel pour créer de petites histoires.

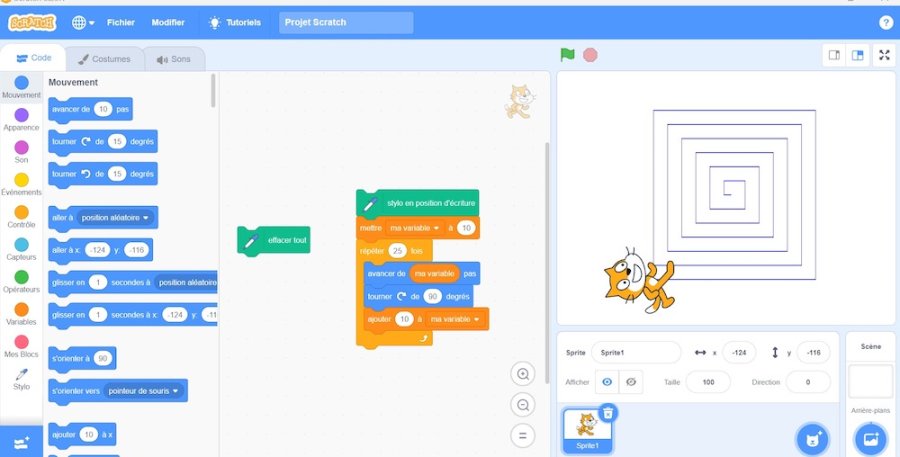
Ces deux dernières activités ont essentiellement été faites en autonomie. Cela n’a pas posé de problème aux élèves qui avaient parfaitement compris la nécessité et l’utilité du langage utilisé grâce à tous les travaux précédemment menés.

Conclusion

Ces différentes activités autour de la verbalisation des algorithmes ont mis en évidence plusieurs difficultés :
d’une part, identifier l’algorithme pour isoler la succession d’actions qui se répète et segmenter les différentes étapes qui le constituent, d’autre part la verbalisation de ces étapes afin de les communiquer et de pouvoir les reproduire.
Les deux difficultés nous ramènent à l’intitulé « des langages pour penser et communiquer » : les deux se rapportent à la capacité d’abstraire, et les différentes activités menées en classe durant plusieurs mois ont eu pour but de guider les élèves dans ce cheminement vers l’abstraction, de faire à concevoir, pour transmettre.

On ne se demande pas, quand on est en retard et que son enfant peine à faire ses lacets, pourquoi c’est si dur à apprendre pour lui. Qu’est-ce qui est si difficile ? La mémorisation d’une procédure à reproduire ? La compréhension ou la verbalisation des instructions ? La traduction de ces gestes en images mentales ? La projection dans le résultat obtenu pour anticiper sa réalisation ?

Au fil du temps, en observant les élèves, en les écoutant communiquer entre eux, en les regardant faire, essayer, se tromper, recommencer, en analysant leurs stratégies d’apprentissage et les obstacles rencontrés, il est apparu qu’en réalité, il y a plus en jeu encore que l’apprentissage du codage, plus que l’apprentissage d’un langage, plus que l’acquisition d’une pensée informatique : c’est le processus de l’apprentissage en soi qui est en question.