Dessiner un polygone régulier, une droite ou un cercle sont faciles avec la tortue Logo (ou Xcas ou GeoGebra ou Sc***ch, etc) ; mais dessiner une conique est nettement plus difficile. Autrement dit, l’univers qu’on explore avec une tortue et son repère mobile, est très différent de celui qu’on explore avec les coordonnées cartésiennes dans un repère fixe. Cet article explore la géométrie de la tortue.
par Alain Busser, Patrice Debrabant
Pour tracer une courbe en repère mobile, l’usage est d’attacher le repère à une tortue (ou l’inverse) : la tortue LOGO (ou une de ses cousines).
Dessiner un polygone régulier, une droite ou un cercle sont faciles avec cette tortue ; mais dessiner une conique est nettement plus difficile. Autrement dit, l’univers qu’on explore avec une tortue et son repère mobile est très différent de celui qu’on explore avec les coordonnées cartésiennes dans un repère fixe.
En pratique, on demande souvent à la tortue de parcourir des polygones (voire des fractales polygonales) et des cercles. Et puis c’est tout.
L’univers de la tortue serait-il plus petit que celui de Descartes ?
Et quid de la complexité d’une courbe ? Peut-on la « mesurer » par celle de son équation cartésienne ou est-ce une nouvelle forme de géocentrisme abusif ?
Aucune tortue n’a été maltraitée durant la rédaction de cet article. Les tortues de l’article sont le plus souvent celles de Sofus 1.4 ; ce logiciel est téléchargeable par clic droit sur le lien ci-dessous :
Article placé sous licence CC-by-SA : http://creativecommons.org/licenses/by-sa/3.0/fr/legalcode
Plan de l’article :
- Polygones (tortues terrestres)
- A) Polygones
- B) Fractales polygonales
- C) L-Systèmes
- Qu’est-ce que c’est que cette tortue ?
- Courbes lisses (tortues marines)
- A) Introduction : le cercle
- B) Bases techniques
- C) Tortue d’exploration
- D) Courbes lisses
- Courbes (paramétriques) connues par ailleurs
- Multi-tortues
1) Polygones
A Popularland [1], la population était constituée de lignes brisées. Les enfants naissaient dans les choux, dessinés par une tortue.
A Popularland, l’objectif était d’être populaire. Et plus on était prévisible, plus on était populaire. Les polygones réguliers étaient admirés, et avaient beaucoup de followers. On aimait la tortue, pas les tordus.
A Popularland, on distinguait les garçons des filles au nombre de côtés : les filles avaient un nombre impair de côtés, et les garçons un nombre pair de côtés.
Les triangles étaient des filles, et les carrés des garçons.
Commençons par un petit recensement de sa population.
Quelles sont les courbes que la tortue peut générer ?
A) Polygones
Introduction
En ce qui concerne les courbes fermées, la tortue trace naturellement des polygones.
Contenu
La première figure qu’on fait tracer par une tortue, c’est presque toujours un carré ; en effet la recette en est très simple :
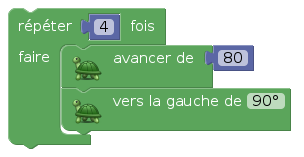
Seulement si on demande à des élèves ayant réussi à tracer un carré, de faire un triangle équilatéral (qui paraît plus simple au premier abord puisqu’il n’y a que 3 répétitions), on obtient en général ceci :
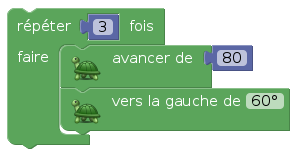
Et le dessin obtenu est un demi-hexagone, pas un triangle :
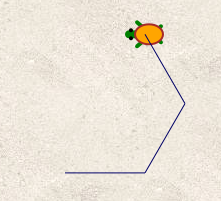
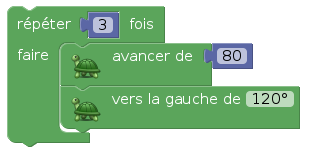
Pour dessiner un triangle, on doit donc tourner de plus que 60° ; déterminer l’angle exact qui referme le triangle est difficile même en terminale : C’est le supplémentaire de 60° et la notion d’angles supplémentaires n’est pas bien maîtrisée en terminale [2]. Le script dessinant un triangle équilatéral est donc celui-ci :
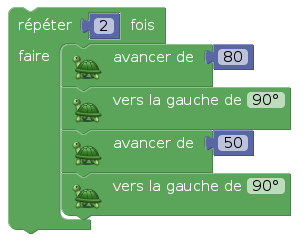
Un rectangle est plus difficile à dessiner parce qu’il ne faut boucler que 2 fois et faire plus de choses dans la boucle :
B) Fractales polygonales
A Popularland, les enfants voulaient à toute force ressembler à leurs parents, et certains allaient jusqu’à se mutiler d’un côté pour y parvenir. Les enfants étaient souvent l’exacte réplique d’un de leur parent.
Quand on faisait la ronde en famille (sur plusieurs générations), on obtenait parfois des courbes bizarres...
flocon de Koch : introduction
L’erreur classique apparaissant lorsqu’on essaye de dessiner avec une tortue, un triangle équilatéral, peut mener à une découverte intéressante : le flocon de Koch. Voici les étapes menant à la version fournie avec Sofus :
Contenu
Tout d’abord, on peut essayer un panachage de rotations de 60° et de 120°, aboutissant à une rotation totale nulle (comme ça la tortue reste horizontale au bout du compte) :

En effet, la rotation vers la droite de 120° annule les deux rotations vers la gauche de 60° chacune :

Pour avoir une fractale, on doit penser à la récursivité : Remplacer chaque instruction « avancer » par l’ensemble des transformations. Pour cela, on définit une fonction « koch » dans laquelle se trouve le programme précédent, mais au lieu de « avancer », on met « koch » :
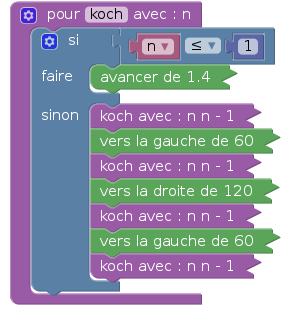
Remarque : on a « réduit » les blocs dans Blockly pour limiter l’extension horizontale du script.
Deux subtilités cependant :
- la fonction « koch » possède un paramètre entier n et les appels à cette fonction se font en remplaçant n par n-1 ;
- au début, un test est effectué pour que, si n est devenu suffisamment petit, la tortue ne fasse qu’avancer un peu : Sa mémoire de travail n’est pas infinie tout de même.
Avec la fonction ainsi définie, on peut aisément dessiner une courbe fractale :

Ce script dessine la courbe que voici (on remarque qu’il a été nécessaire de placer la tortue à gauche de l’écran pour voir la courbe en entier) :
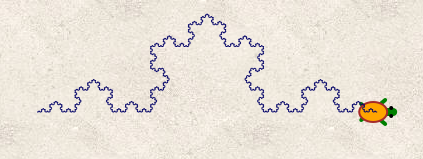
On peut généraliser la courbe à celle de Cesaro, mais pour cela il faut idéalement passer par la géométrie dynamique. Voir dans ce numéro l’article d’Yves Martin sur DGPad, qui utilise aussi Blockly, mais sans le mode tortue.
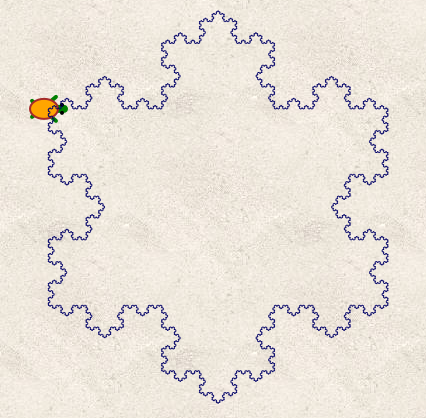
Maintenant qu’on a une courbe fractale, il suffit de remplacer chaque côté d’un triangle équilatéral par cette courbe, pour avoir le flocon de von Koch :

Le dessin est bien celui du flocon :
A Popularland, les enfants suivaient des cours d’eugénisme et étaient consultés pour valider les nouveaux profils.
En effet, il s’agissait de créer des générations populaires. Et l’avis des enfants était très représentatif des futures tendances.
On leur avait donc demandé si le profil von Koch serait populaire. Il y avait débat sur l’avenir de ce profil garçon. C’était mauvais signe, ce profil pouvait faire réfléchir.
- M’sieur M’sieur, je comprends pas !
- C’est quoi le problème maintenant ?
- Ben pour dessiner un triangle équilatéral, vous avez fait tourner la tortue vers la gauche et là, vous la faites tourner vers la droite...
- Oui, effectivement , si j’avais conservé les 3 rotations de 60° vers la gauche, les renflements du flocon eussent été tournés vers l’intérieur et je n’aurais pas eu un vrai flocon.
- Ah bon c’est juste ça, mais M’sieur au fait...
- Quoi encore ?
- Qu’est-ce que ça aurait donné si vous aviez fait tourner la tortue vers la gauche ?
- Sofus est là pour expérimenter : Essaye pour voir, et regarde ce que ça donne...
- Trop fatigant, ça me soûle ! Je vote pas pour ce profil. J’aime pas.
Autres fractales : introduction
Par un procédé similaire, la tortue peut tracer d’autres fractales polygonales. En particulier, la tortue peut monter aux arbres.
Contenu
Pour tracer une courbe de Von Koch, la tortue a compensé les rotations à gauche par des rotations à droite. Si, en plus, on compense les avancées par des reculs, la tortue peut dessiner des structures arborescentes :
La tortue a bien dessiné sur le sable, non pas le doux visage d’Aline, mais un polygone qui ressemble à un arbre (surtout si on a mis la couleur du crayon sur du vert foncé) :

La « compensation » peut aussi consister en un petit parcours qui s’achève en revenant à la position initiale.
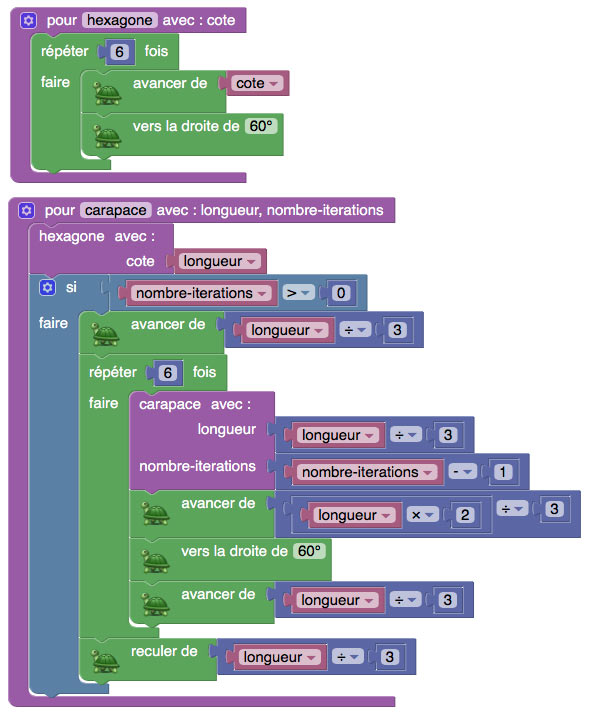
La tortue étant narcissique, elle a tenté de tracer sa propre carapace.
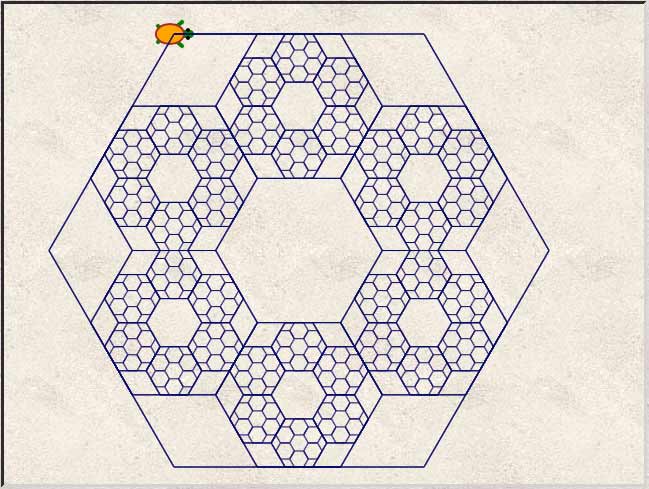
On peut comparer le script de la même fractale écrite dans le langage de GéoTortue.
Le script des procédures est le suivant :
- pour hexagone cote
- rep 6 [ av cote; td 60 ]
- fin
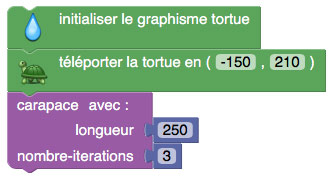
- pour carapace longueur nombre_iterations
- hexagone longueur
- si (nombre_iterations>0) alors [
- av longueur/3;
- rep 6 [ carapace longueur/3 nombre_iterations-1 ; av 2*longueur/3; td 60; av longueur/3];
- re longueur/3]
- fin
Le code en ligne est plus facilement compréhensible que le code en blocs visuels. C’est un des problème de la programmation visuelle par blocs.
GéoTortue utilise une syntaxe particulière très proche de celle du LOGO. Pour comparaison, voici la version Python du même script (chacun sait que les serpents et les tortues s’entendent très bien) :
- from turtle import *
- def hexagone(cote):
- for pas in range(6):
- forward(cote)
- right(60)
- def carapace(longueur,nb_iter):
- hexagone(longueur)
- if nb_iter > 0:
- forward(longueur/3)
- for ecaille in range(6):
- carapace(longueur/3,nb_iter-1)
- forward(2*longueur/3)
- right(60)
- forward(longueur/3)
- backward(longueur/3)
- speed(0)
- carapace(81,3)
Et voici le code pour la tortue CaRMetal :
- fonction hexagone(cote) {
- pour var j allant de 1 à 6 {
- av(cote);
- tddeg(60);
- }
- }
- fonction carapace(l,nbIter){
- hexagone(l);
- si (nbIter>0) {
- av(l/3);
- pour var i allant de 1 à 6 {
- carapace(l/3, nbIter-1);
- av(2*l/3);
- tddeg(60);
- av(l/3);
- }
- re(l/3);
- }
- }
- carapace(2,3);
2) Qu’est-ce que c’est que cette tortue ?
A Popularland, c’était donc une tortue qui fabriquait les enfants. Cette tortue avait un petit cerveau et n’aimait pas les commandes compliquées. Elle répondait à deux ordres simples : avancer et tourner, qui étaient traduits littéralement dans la langue du pays où se trouvait la tortue.
Dans certains pays, la langue parlée était le Javascript, dans d’autres le Python, etc. Dans certaines provinces indépendantistes, on parlait le patois du coin. C’était le cas par exemple de la GéoTortue, qui parlait une langue très inspirée du Logo, et qui en gardait l’esprit. Le Logo était la langue parlée par la toute première Tortue.
Le concept de tortue : introduction
Commençons par dissiper un malentendu : on parle de tortue LOGO, mais la tortue n’est pas foncièrement LOGO. Le Logo est un langage de programmation « simplifié » (mais Turing-complet). La première tortue, par choix de son auteur Seymour Papert, parlait le Logo, ce qui explique l’association des deux termes.
Contenu
Un précurseur (peut-être même le précurseur) en ce domaine fut William Grey Walter qui, dans les années 1940, a mis au point des robots capables de se déplacer (par translations ou rotations combinées) et de laisser éventuellement une trace au sol. Pour protéger l’électronique de ces robots, Grey Walter les a munis de carapaces métalliques qui ont rapidement évoqué des tortues cybernétiques, ce qui a valu à ces robots le nom de tortues de Bristol. 20 ans plus tard, ce fut la création de Logo (langage), inspiré de Lisp, langage de programmation destiné aux enfants et devant leur permettre de programmer récursivement (essentiellement des chaînes de caractères). Or pour que des enfants comprennent une séquence d’instructions décrivant un algorithme, il vaut mieux éviter que l’algorithme soit numérique : Comment expliquer à un enfant qui ne connaît pas encore la division, le fonctionnement de l’algorithme d’Euclide ? Pour permettre à ses « cobayes » de programmer un micromonde non exclusivement numérique, Papert a choisi de simuler la tortue de Grey Walter, par des dessins vectoriels sur l’écran de l’ordinateur. Le succès en fut tel que non seulement tout le monde a oublié l’original de Grey Walter, mais en plus tout le monde s’imagine que « logo = tortue ». Or, du fait qu’elle est relativement facile à programmer, la tortue et son graphisme a été incorporée à d’autres langages que Logo, comme par exemple Xcas, Python ou GeoGebra ; plus récemment, celle des jeux Blockly est à elle seule une séquence pédagogique pour la classe de 5e.
En ce qui concerne la tortue elle-même, ou plutôt son environnement, certaines tortues vivent dans un environnement dans lequel on peut zoomer, et c’est un atout considérable pour ce qui va suivre.
C’est le cas de la GéoTortue et des deux tortues que l’on va construire avec CaRMetal.
Revenons maintenant aux généralités, et à ce qui fait une tortue.
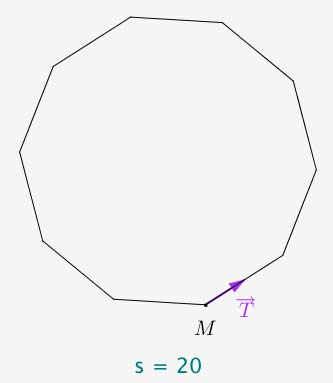
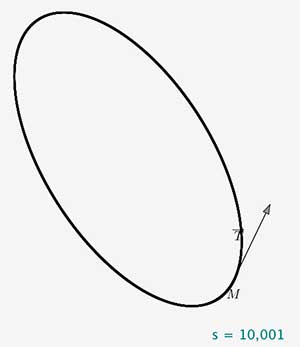
En fait, cette tortue porte sur son dos le repère de Frenet (ou son équivalent dans les cas où ce repère n’est pas défini rigoureusement).
Pour mémoire, on appelle repère de Frenet en un point M régulier d’une courbe, le repère orthonormé direct formé par le point de la courbe, le vecteur tangent $\vec{T}$ et le vecteur normal $\vec{N}$.
La tortue a une vitesse de norme constante (cela paraît raisonnable pour un animal). Cela invite à utiliser l’abscisse curviligne s.
Car si on utilise s comme unité de temps, alors la vitesse a pour norme 1.
On a alors :
$\dfrac{dM}{ds}=\vec{T}\quad$ et $\quad\dfrac{d}{ds}\vec{T}=k\vec{N}\quad$ avec $\quad k=\pm \dfrac{1}{R}$ où $R$ est le rayon de courbure.
Si on souhaite construire une courbe régulière par intégration de s, à chaque étape infinitésimale, il y a deux modifications à faire :
- $dM=ds \vec{T}$
- $d\vec{T}=\dfrac{ds}{R}\vec{N}$
La première modification consiste à faire avancer le point M (dans le sens du vecteur vitesse).
La deuxième modification consiste à tourner.
Ce choix de l’abscisse curviligne est plus intéressant (ne serait-ce que pour des questions de complexité algorithmique) pour des courbes régulières que pour des polygones.
Par ailleurs, il n’est pas nécessaire de commencer par s=0 mais les équations données ci-dessous sont intrinsèques, ce qui ne détermine la courbe qu’à un déplacement près. En d’autres termes, il peut être nécessaire de téléporter et donner une orientation initiale à la tortue.
Pour bien voir ce qui se passe, on va le faire avec les outils (un peu) méconnus du logiciel CaRMetal :
Essayons par exemple de construire une chaînette, d’équation intrinsèque explicite $R=1+s^2$.
CaRMetal dispose de l’outil segment de longueur fixe qui est parfaitement adapté pour modéliser le vecteur $\vec{T}$.
On peut aussi modéliser très facilement l’abscisse curviligne en utilisant les fonctions sum et d. Le point M générant la courbe, une expression égale à sum(d(M) ;0) donne l’abscisse curviligne de M.
En pratique, il faut créer un segment u de longueur fixe 1 qui correspond à $-\vec{T}$. Ce « segment » a pour origine un point A (que l’on peut tracter) et pour extrémité un point M (le point de la courbe qui laissera une trace).
Ensuite, on crée une expression s égale à sum(d(M) ;0) pour l’abscisse curviligne de M.
Le vecteur $\vec{T}$ est tracé pour la visualisation.
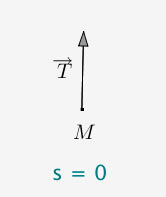
Pour tracer la courbe, on active la trace de M.
On crée ensuite le script suivant :
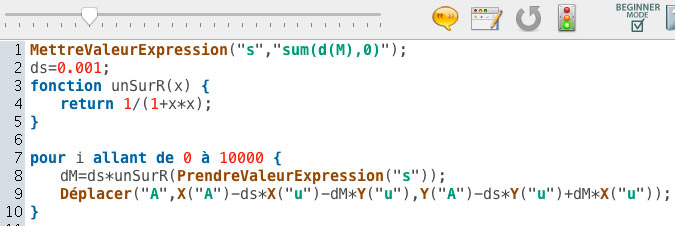
$\vec{T}$ a pour coordonnées (-x(u),-y(u)), donc on peut prendre pour $\vec{N}$ le vecteur de coordonnées (-y(u),x(u)).
On déplace A de $dM=ds \vec{T}$ pour déplacer le point M, puis de $d\vec{T}=\dfrac{ds}{R}\vec{N}$ pour modifier le vecteur $\vec{T}$ (sans déplacer M).
En lançant le script, on obtient la chainette :

On peut alors séparer les deux actions dans le script :
- MettreValeurExpression("s","sum(d(M),0)");
- ds=0.001;
- fonction unSurR(x) {
- return 1/(1+x*x);
- }
- pour i allant de 0 à 10000 {
- dM=ds*unSurR(PrendreValeurExpression("s"));
- Déplacer("A",X("A")-ds*X("u"),Y("A")-ds*Y("u"));
- Déplacer("A",X("A")-dM*Y("u"),Y("A")+dM*X("u"));
- }
Ligne 9, on avance. Ligne 10, on tourne.
Si on ne fait que tourner, à rayon de courbure constant, on tourne d’un angle égal à $\dfrac{\Delta s}{R}$
On va donc créer une fonction td (tourner à droite) et une fonction tg (tourner à gauche) qui pourront être utilisées dans le script :
- fonction td(x) {
- Déplacer("A",X("A")-x*Y("u"),Y("A")+x*X("u"));
- }
- fonction tg(x) {
- Déplacer("A",X("A")+x*Y("u"),Y("A")-x*X("u"));
- }
- MettreValeurExpression("s","sum(d(M),0)");
- ds=0.001;
- fonction unSurR(x) {
- return 1/(1+x*x);
- }
- pour i allant de 0 à 10000 {
- dM=ds*unSurR(PrendreValeurExpression("s"));
- Déplacer("A",X("A")-ds*X("u"),Y("A")-ds*Y("u"));
- td(dM);
- }
Seulement, ces fonctions tg et td ne fonctionnent que pour une variation infinitésimale de s. On va donc les modifier pour obtenir une réelle rotation d’angle x.
- fonction td(x) {
- Déplacer("A",X("M")-X("u")*Math.cos(x)-Y("u")*Math.sin(x),
- Y("M")-Y("u")*Math.cos(x)+X("u")*Math.sin(x));
- }
- fonction tg(x) {
- Déplacer("A",X("M")-X("u")*Math.cos(x)+Y("u")*Math.sin(x),
- Y("M")-Y("u")*Math.cos(x)-X("u")*Math.sin(x));
- }
Attention, ces fonctions tg et td sont en radians.
On ajoute aussi une fonction av (avancer) et une fonction re (reculer) pour disposer des deux instructions de base de la tortue :
- fonction av(x) {
- Déplacer("A",X("A")-x*X("u"),Y("A")-x*Y("u"));
- }
- fonction re(x) {
- Déplacer("A",X("A")+x*X("u"),Y("A")+x*Y("u"));
- }
On peut ajouter tgdeg pour disposer d’une fonction tourner en degrés.
On peut aussi modifier la fonction av pour qu’elle trace un segment (et on peut alors désactiver la trace de M).
On obtient alors une tortue CaRMetal qui comprend les instructions de base du LOGO, et qui permet de zoomer. (Remarque : on créera plus loin une autre tortue, plus originale, avec CaRMetal.)
Et par exemple le script suivant trace un polygone régulier à 10 côtés :

Et on pourrait utiliser l’abscisse curviligne.
3) Courbes lisses
A Popularland, on vouait un culte au cercle.
Celui-ci était considéré comme une perfection, et se voyait en conséquence doué de toutes les capacités, en particuler celle, démiurgique, d’avoir créé le monde.
Le cercle était à l’image du polygone régulier et en constituait une limite asymptotique. Il était d’une nature différente et unique en son genre. Il n’en fallait pas plus pour être un Dieu.
Réciproquement, la vénération du cercle renforçait l’aplomb de ses représentants sur terre, les polygones réguliers.
On s’était posé la question de savoir s’il était sacrilège d’essayer de représenter le cercle, et d’en donner ainsi une image fausse (car la tortue ne pouvait tracer que des lignes brisées). De mauvais esprits prétendaient que comme ce Dieu était désespérément à l’image du polygone, il était inepte de refuser de le représenter. Que c’était ajouter du ridicule au ridicule.
Tout ce qui ne tendait pas au cercle était considéré comme vicieux.
Un jour, un polygone mal fichu affirma que c’était un cercle vicié et que l’élévation vers Dieu pouvait se faire dans des formes différentes, et pas seulement celle des polygones réguliers.
Quand on le somma de renoncer à cette hérésie, il répondit
- Vous chariez, là !
Cette réflexion lui valut l’étêtage.
- Le plus triste, dit-il, c’est que je vais ressembler à un polygone régulier...
A) Introduction : le cercle
Le cercle frontière
Le cercle est un premier exemple de courbe lisse que l’on peut tracer avec la tortue.
Contenu
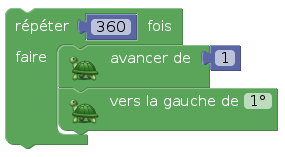
Une fois qu’on sait dessiner des polygones réguliers, on peut dessiner un cercle très probant, sous la forme d’un polygone régulier ayant 360 côtés, pour lequel on tourne d’un degré à chaque fois :
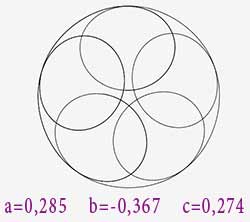
On peut définir le cercle par ce tracé et faire une rosace formée de 6 cercles :
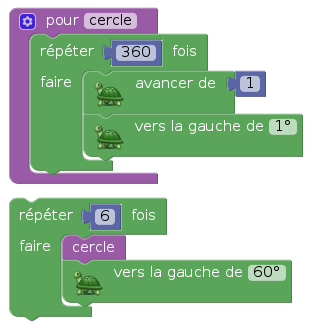
Voici la rosace obtenue :

Exercice de géométrie : De combien de pixels la tortue doit-elle avancer à chacun des 360 pas pour que le cercle ait un rayon donné (par exemple 160 pixels) ?
C’est un exercice de trigonométrie en fait : Décomposer le polygone en 360 triangles isocèles et faire de la trigonométrie sur l’un d’eux.
B) Bases techniques
Tracer une courbe lisse
Dans le cas du cercle, la courbure est constante. Généralisons un peu.
Contenu
Il faut gérer une abscisse curviligne s. Le principe est de choisir un pas ds et de tracer la courbe.
La courbe peut être affinée en diminuant le pas et (pour l’instant) en relançant le tracé.
Avec la tortue CaRMetal donnée plus haut, s est gérée par une expression et on peut zoomer. La base de script est la suivante :
- ds=0.01;
- fonction unSurR(x) {
- return 1/(1+x*x);
- }
- pour i allant de 0 à 1000 {
- dM=ds*unSurR(PrendreValeurExpression("s"));
- av(ds);
- td(dM);
- }
Et voici le fichier CaRMetal :
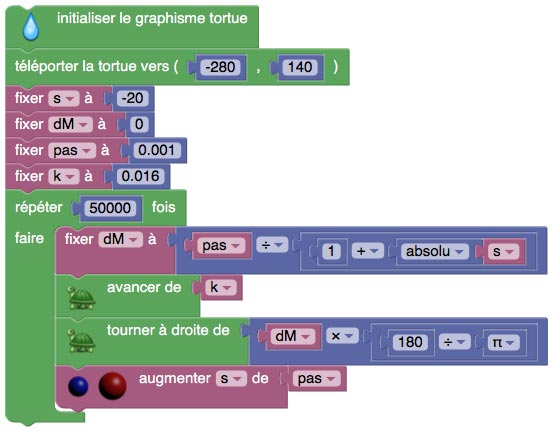
Pour la tortue de Sofus, on gère s à l’aide d’une variable.
Et on n’a pas la possibilité de zoomer dynamiquement.
Pour obtenir un effet de zoom, mais statique, on peut définir un grossissement k. k s’applique au déplacement (fonction av) mais ni à la modification de dM ni à celle de s.
Dans le langage de CaRMetal, on obtiendrait un script de ce type :
- s:=0;
- ds=0.01;
- k:=0.01;
- fonction unSurR(x) {
- return 1/(1+x*x);
- }
- pour i allant de 0 à 1000 {
- dM=ds*unSurR(s);
- av(k);
- td(dM);
- s:=s+ds;
- }
Remarques :
ce script est fonctionnel avec CaRMetal.
k est beaucoup plus petit pour CaRMetal que pour Sofus (dont l’échelle est en pixels).
Pour la chaînette avec Sofus, le script est le suivant :
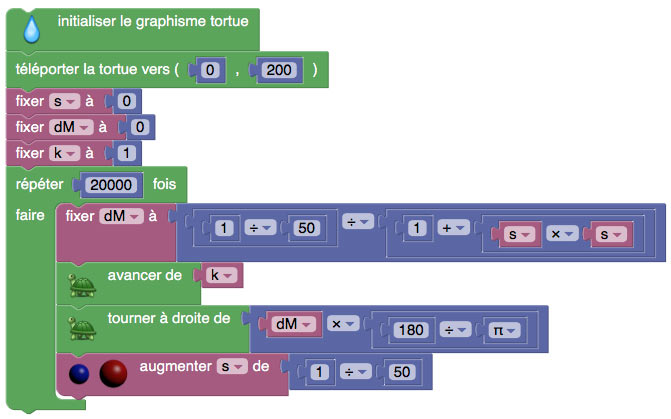
On a ajouté un petit complément de conversion à la fonction tourner à droite pour tourner en radians.
On obtient la courbe suivante :

C) Tortue d’exploration
Tortue du troisième type
Les mouvements dans l’eau étant plus fluides, on peut considérer que la tortue soumise à la géométrie différentielle, qui trace des courbes lisses, est une tortue marine alors que celle qui trace des polygones est une tortue terrestre.
On va maintenant créer une tortue du troisième type : une tortue dynamique d’exploration.
Contenu
« Bouh, encore une tortue ! », vous allez me dire....
Oui, mais cette tortue est maousse costaud.
En fait, il s’agit d’une tortue toute simple, mais dynamique.
Elle ne va pas spécialement vite, mais elle a de l’estomac, et peut, telle la baleine de Jonas, avaler des paramètres vivants.
On la crée avec CaRMetal, qui permet ce genre de prodige.
L’objectif est d’explorer une équation intrinsèque explicite avec des paramètres qui seront dynamiques.
Prenons par exemple l’équation $R=\dfrac{s+a}{s}$
a est un paramètre.
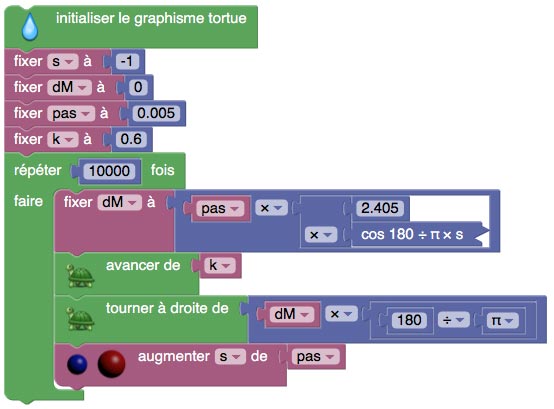
Voici le script de cette tortue :

a est une expression.
ds est également une expression.
(En pratique, ce sont des curseurs).
Remarque : on utilise rcos et rsin pour travailler avec des angles en radians.
On crée les curseurs ds et a.
On crée un point M.
On obtient alors une courbe (approchée) dynamique en ds et a.
Et voici ce que l’on peut observer :
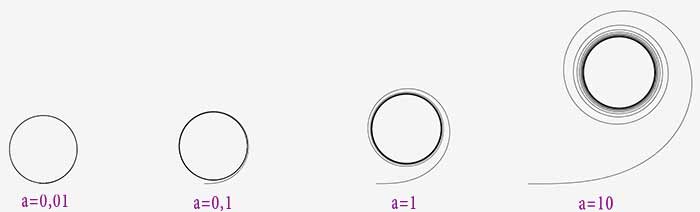
Augmenter ds revient à aller dans le futur.
Pour a = 0, on a un rayon de courbure constant, la courbe est un cercle de rayon 1.
sinon, a diminue progressivement et tend vers 1 : on a un cercle asymptote.
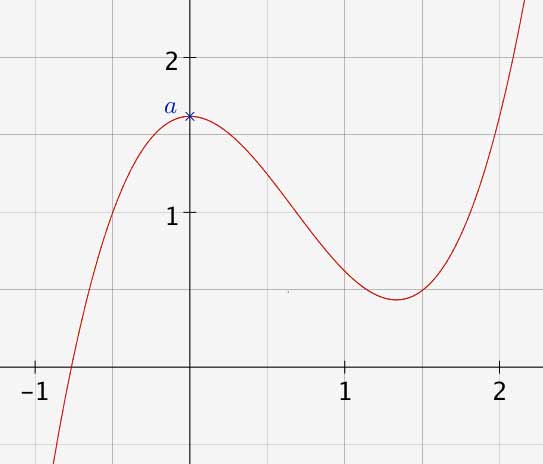
Prenons un autre exemple où R est un polynôme de s : $R=s^3-2s^2+a$
Cette fois, on a dans le script :
- dM="+ds*1/("+s[i]+"^3-2*"+s[i]+"^2+a)";
La courbe de la fonction R(s) est :
On obtient l’évolution suivante en fonction de a :
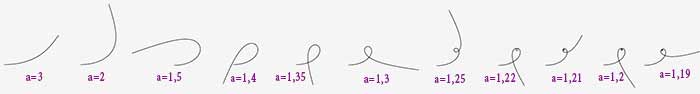
A mesure que R s’approche de 0, la courbe boucle sur elle-même plusieurs fois. On obtient différents niveaux de boucles.
D) Courbes lisses
Exemples sans paramètres
Voyons ce qui se passe pour certaines équations intrinsèques simples :
$R=\dfrac{1}{s}$
$R=\dfrac{1}{abs(s)}$
$R=\dfrac{1}{s^2}$
$R=\dfrac{1}{cos^2(s)}$
$R=\dfrac{1}{cos(s)}$
$R=1+abs(s)$
Contenu
On va prendre s variant entre -∞ et +∞.
Pour $R=\dfrac{1}{s}$, autrement dit quand l’angle de rotation est proportionnel à s, on obtient ce script :
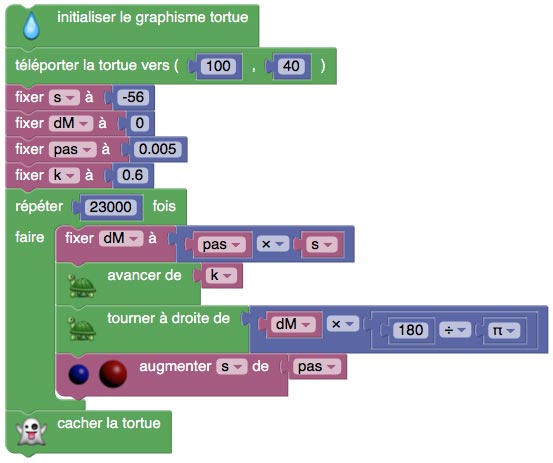
La courbe obtenue est alors une spirale de Cornu (ou clothoïde) :

Cette courbe possède un centre de symétrie (pour s=0). On peut avoir une variante avec un axe de symétrie en prenant la valeur absolue de s au lieu de s :
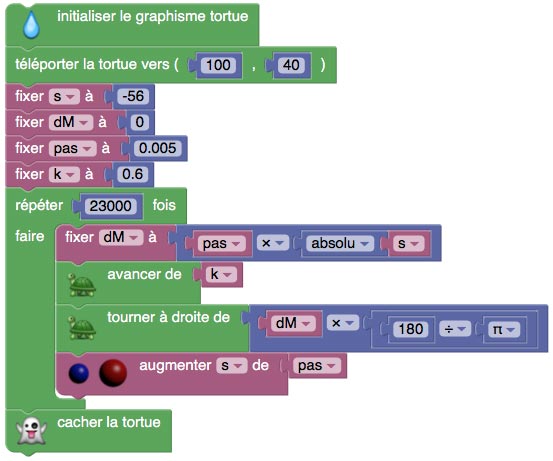
Le résultat n’est guère surprenant :
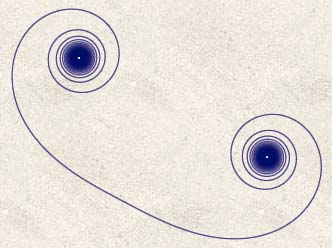
Une variante consisterait à prendre le carré de s plutôt que sa valeur absolue.
Juste pour le plaisir, commençons par faire les choses naïvement, en prenant un pas de 1 et en tournant en degrés. On obtient de charmantes arabesques

Le script ayant engendré cette figure est celui-ci :
Seulement, il y a un hic : cette figure est totalement fantaisiste, on devrait obtenir une figure semblable à celle obtenue pour $R=abs(s)$.
De fait, le script suivant :
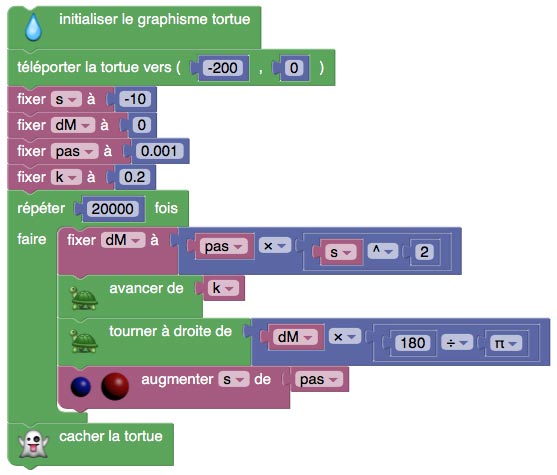
donne la figure réelle :

Encore, encore !
Poursuivons avec deux autres exemples, avec des fonctions trigonométriques, ce qui permet d’avoir des courbes fermées. C’est un avant-goût de ce que l’on fera plus loin avec la tortue dynamique de CaRMetal :
1) Une sorte d’ovale (non ce n’est pas une ellipse, celle-ci est nettement plus compliquée, voir aussi plus bas) :
$R=\dfrac{1}{2.cos^2(s)}$
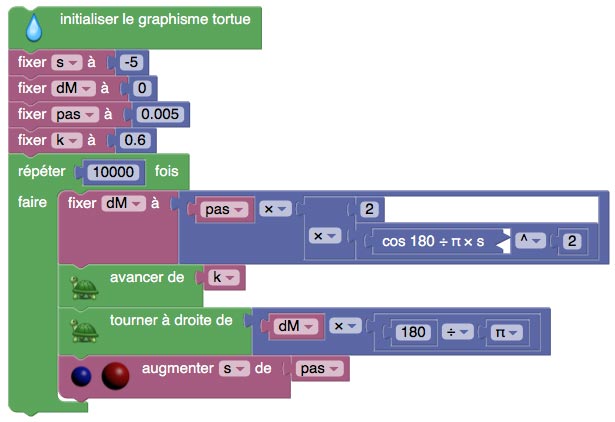
On pourrait penser que le paramètre 2 devant le $cos^2(s)$ est arbitraire.
Faisons appel à la tortue ninja de CaRMetal pour voir ce qu’il en est vraiment.
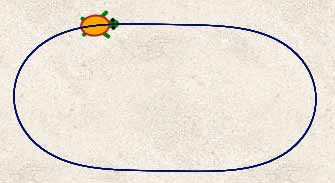
On étudie la famille de courbes : $R=\dfrac{1}{a.cos^2(s)}$ et on se limite aux courbes fermées.
Pour des petites valeurs de a, et des valeurs qui tombent pile, on peut obtenir un polygone aux coins arrondis...
Toujours avec les valeurs qui tombent pile, pour a plus grand, on obtient des fleurs.
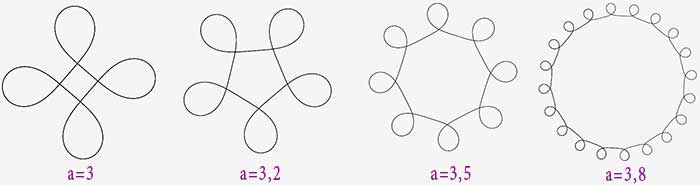
Puis on obtient des polygones qui ont des coins en forme de boucles
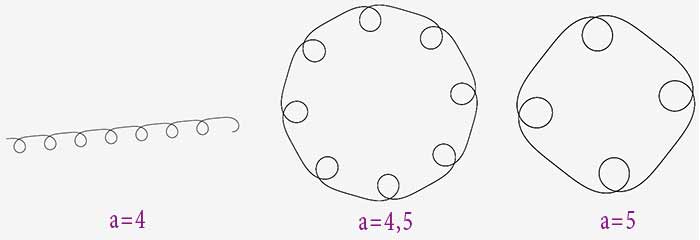
Des valeurs de a qui ne tombent pas pile donnent aussi des specimens intéressants :
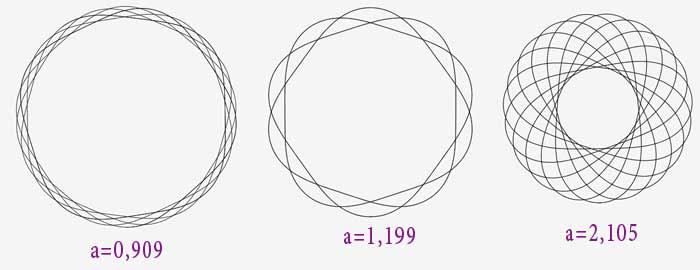

Pour la route
2) un huit (pas une lemniscate non plus) :
$R=\dfrac{1}{2,405.cos(s)}$

Là encore, on peut se demander si la valeur 2,405 peut être remplacée par une autre.
L’étude de la famille de courbes $R=\dfrac{1}{a.cos(s)}$ montre que non.
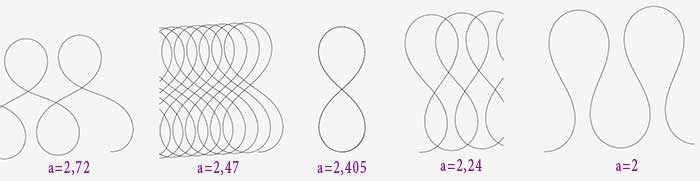
Mais tout ça n’est pas raisonnable du point de vue de la thermodynamique : Plus la tortue avance, moins il lui reste d’énergie et tourner de plus en plus accélérera sa fatigue. Au contraire, la tortue devrait, pour s grand, tourner de moins en moins, et la fonction exprimant la courbure en fonction de s devrait tendre vers 0 à l’infini. Pour avoir de telles courbes plutôt simples, on peut prendre l’inverse de fonctions comme 1+s² (chaînette), par exemple l’inverse de 1+abs(s) :
On pourrait penser que la courbe obtenue va ressembler à une chaînette et à une parabole. Mais il n’en est rien :

On va maintenant faire deux études de cas :
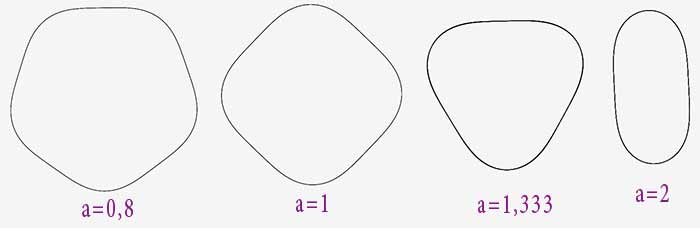
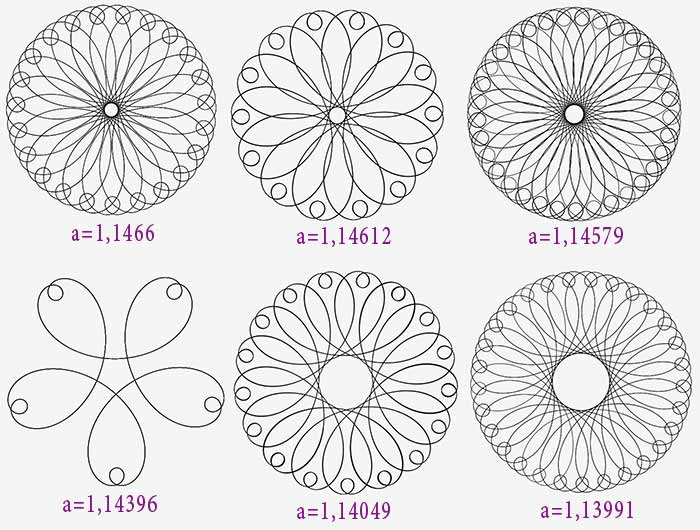
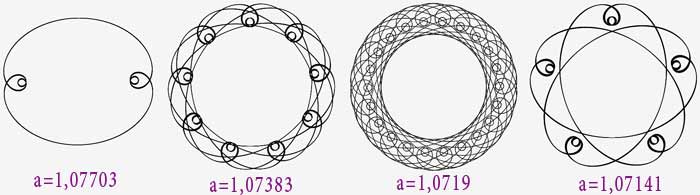
R=a+cos(s) : Whaou !!!
On va s’intéresser aux courbes $R=a+cos(s)$ pour a>1, et en particulier à celles qui sont fermées (et qui sont obtenues pour des valeurs discrètes de a).
On va diminuer progressivement le paramètre a et observer l’allure de la courbe.
Remarque : on se limite ici aux courbes fermées, et, attention, les différentes courbes présentées ont des échelles différentes.
2>a>5/3
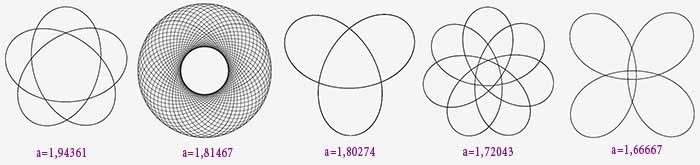
On voit bien l’effet du rayon de courbure.
A mesure que a diminue, la partie centrale rétrécit : un peu au delà de a = 5/3, on voit que l’on arrive à une frontière, et qu’il va y avoir une « inversion »...
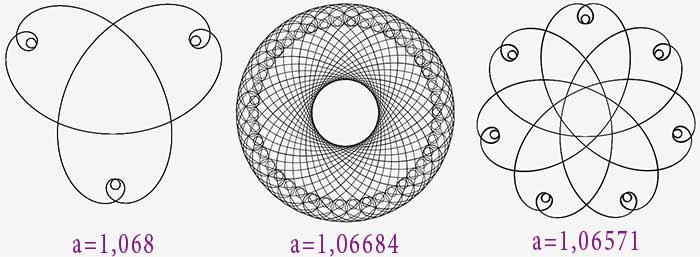
5/3>a>1,5
A la frontière, les courbes sont particulièrement esthétiques : le tortue nous fait des fleurs.
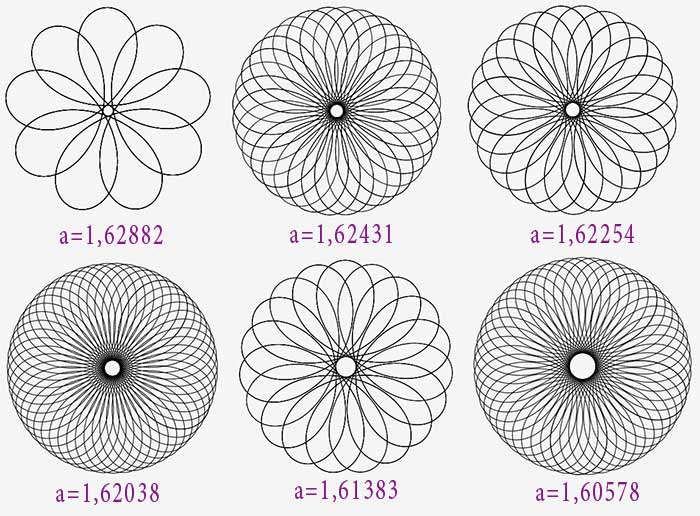
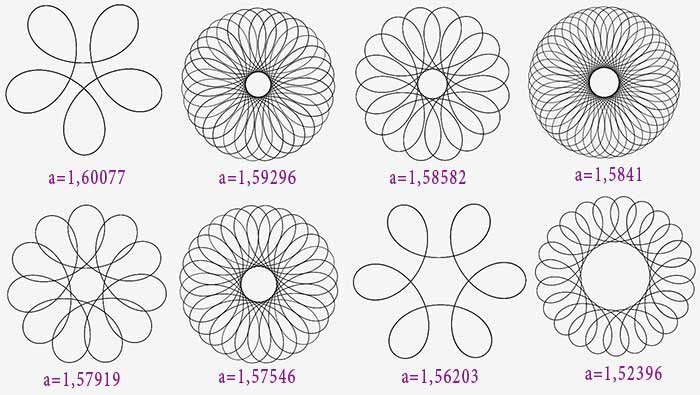
On voit que l’évolution se fait maintenant en sens inverse : la partie centrale s’élargit... jusqu’à...
1,5>a>1,4
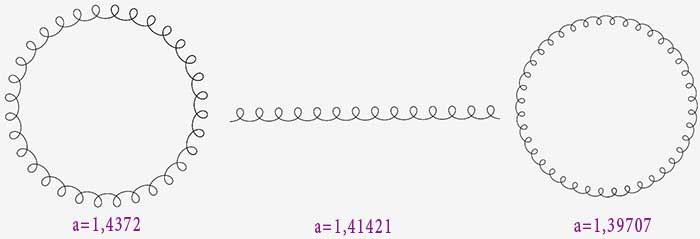
Pour $a=\sqrt{2}$, la courbe s’ouvre ! On obtient en quelque sorte une courbe fermée avec un rayon infini.
Puis la courbe se referme à nouveau avec une inversion.
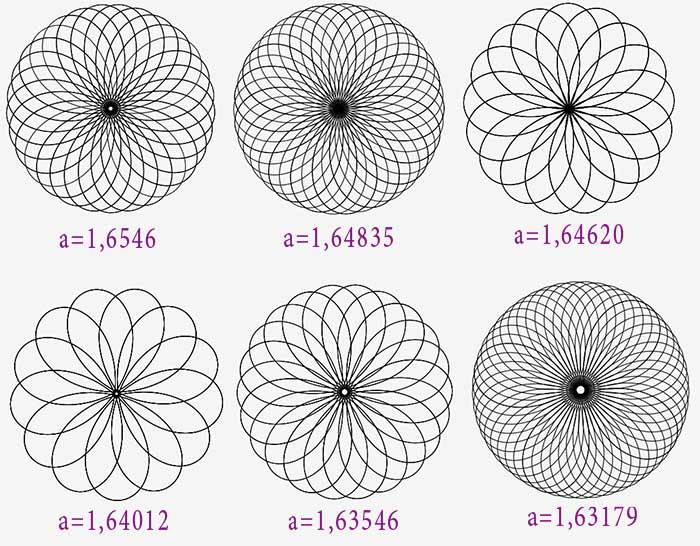
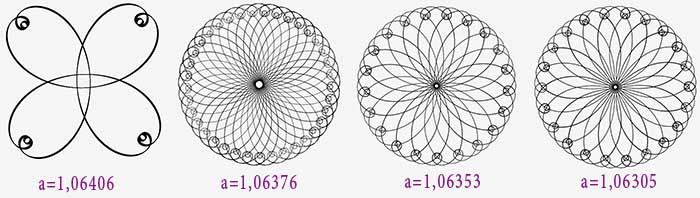
1,4>a>1,15
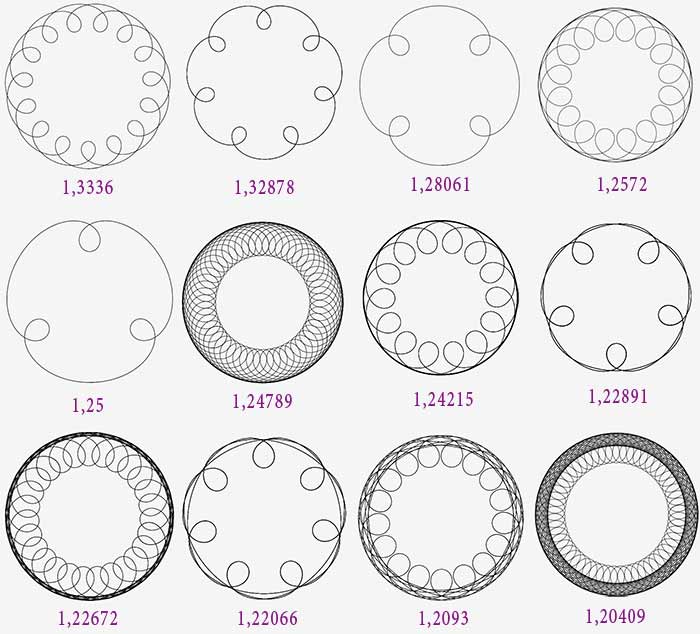
Progressivement, le mouvement de la grande boucle s’affirme.
A partir de a = 1.2, on a fait un demi-tour donc il y aura chevauchement des grandes boucles.
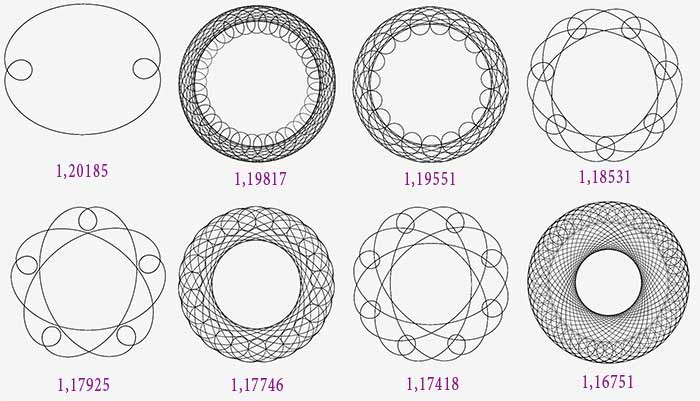
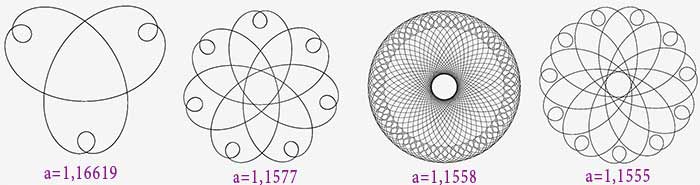
Pour a=1.6619 on obtient une bitoïde d’ordre 3.
Une zone centrale apparaît comme précédemment et va en rétrécissant.
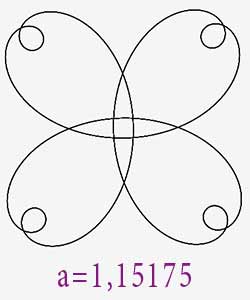
Pour a= 1.15175 une bitoïde d’ordre 4 annonce l’inversion.
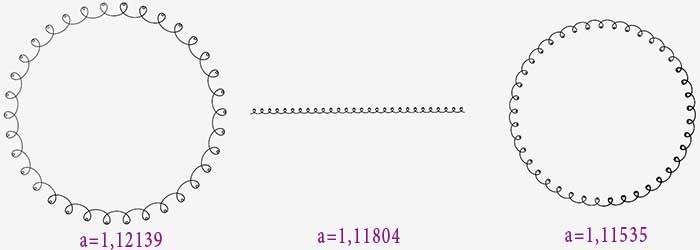
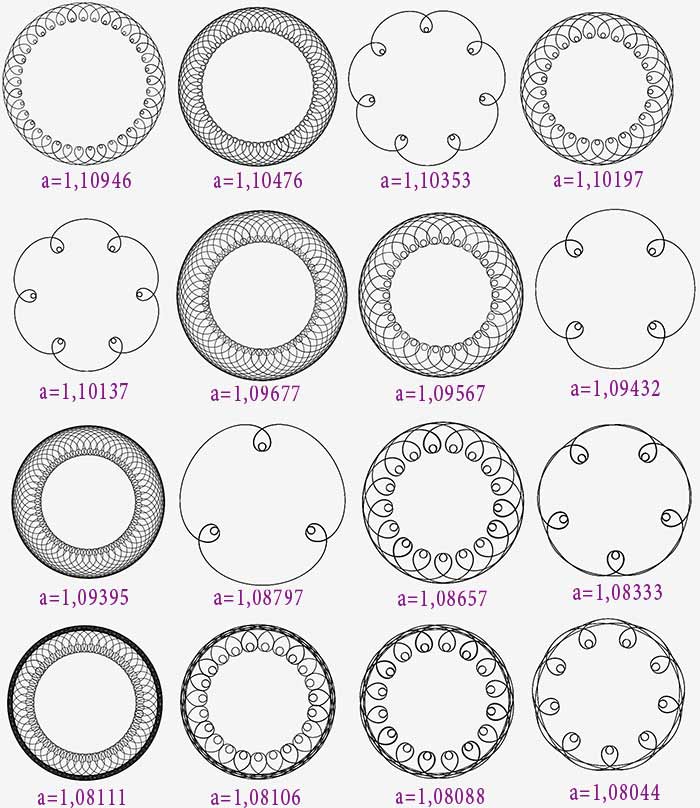
1,15>a>1,12
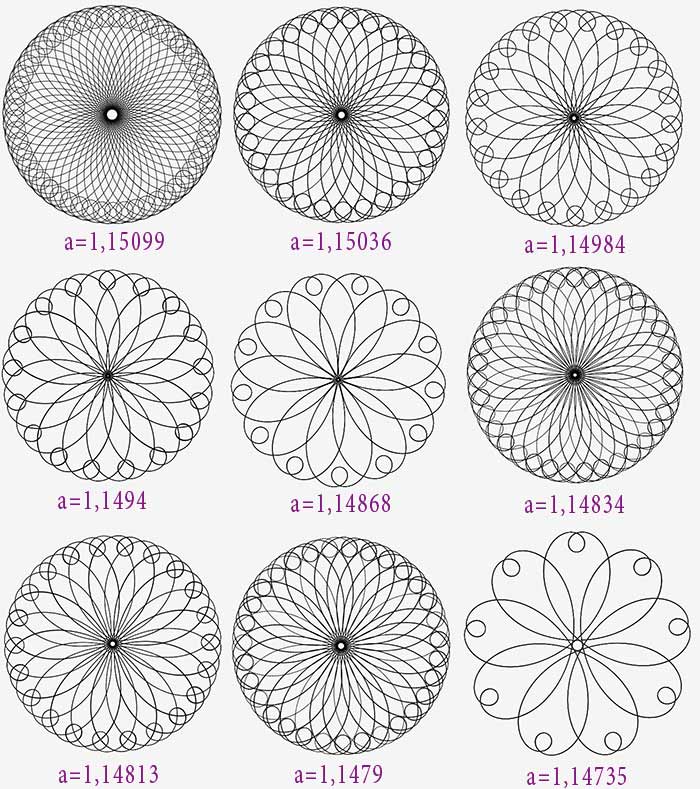
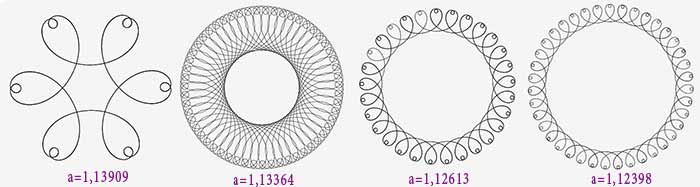
On observe la même évolution que précédemment, à ceci près que les petites boucles contiennent elles-mêmes une petite boucle (un ocelet).
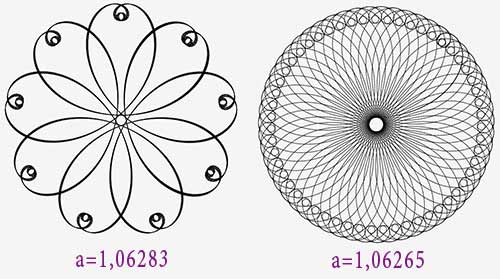
1,12>a>1
L’évolution devient présivisible : ouverture de la grande boucle, inversion, etc
Voici la figure CaRMetal :
Et sur une idée d’Yves Martin, voici la figure dynamique en ligne réalisée avec DGPad.
Cette fois, la courbe est une liste dynamique de points, que l’on peut construire par programmation visuelle par blocs (Blockly) ou de façon plus conventionnelle comme on l’a fait ici.
Le script de la liste de points est le suivant :
- tab=[];
- tab.push(M);
- var P, rM;
- var s=0;
- var angle=0;
- var ancP=M;
- for (var i=1;i<nbPoints;i++) {
- s+=ds;
- rM=ds/(cos(s)+a);
- P=[ancP[0]+ds*cos(angle),ancP[1]+ds*sin(angle)];
- tab.push(P);
- angle+=rM;
- ancP=P;
- };
- tab
Pour rester dans le même esprit, on peut prendre R = un polynôme de cos(s) qui ne s’annule pas.
Et on peut décomposer sur la base des polynômes de Tchebychev.
Pour les polynômes de degré 2, on modifie le script ainsi :
- dM="+ds/(b*rcos("+s[i]+")+c*rcos(2*"+s[i]+")+abs(b)+abs(c)+a)";
On peut alors observer l’apparition de nouveaux specimens intéressants.
R=b.cos(s)+c.cos(2s)+abs(b)+abs(c)+a
Vraiment, cette tortue nous fait des fleurs.
4) Courbes paramétriques
A Popularland, la mythologie évoquait des aliens panthéistes vénérant des dieux qui portaient le nom de courbes paramétriques.
Avec l’avénement de nouveaux critères de perfection, ceux-ci revinrent à la mode : quand un polygone ne ressemblait à rien, il prétendait qu’il était à l’image d’une courbe paramétrique.
Une erreur scientifique répandue consistait à dire :
- j’ai du chromosome X, du chromosome Y. Donc je suis à l’image d’une équation paramétrique.
Introduction
Comme on vient de le voir, la tortue est capable de tracer des courbes qui impressionnent les observateurs dans le repère fixe.
Mais peut-elle aussi tracer des courbes plus banales pour les cartésiens, à savoir les courbes paramétrées ?
La réponse est oui.
Pour exemple, on va tracer une ellipse.
Contenu
L’équation paramétrique est
$x=a cos(t)$
$y=b sin(t)$
On définit $c=\sqrt{a^2-b^2}$ la demi-distance focale, et $e=\dfrac{c}{a}$ l’excentricité.
Pour l’abscisse curviligne, on obtient $ds=a\sqrt{1-e^2cos^2(t)} dt$
et pour rayon de courbure : $R=\dfrac{a^2}{b}(1-e^2cos^2(t))^{\frac{3}{2}}$
On peut alors utiliser ces formules pour tracer l’ellipse.
Pour la tortue CaRMetal, le script (version trace de M) est le suivant

On obtient l’ellipse avec une précision suffisante :
Si on veut construire le script en programmation visuelle par blocs, c’est plus pénible. Il faut se fader les opérations...
5) Multi-tortues
A Popularland, l’évolution prit un tour particulier : la Tortue se mit à se reproduire par mitose.
Et les Tortues ainsi engendrées se mirent à se chercher, à se viser.
Sur les sites de rencontres entre polygones, apparut un nouvel atout : « mes courbes ».
Courbe de poursuite, courbe du chien, … On voyageait.
Introduction
La possibilité d’utiliser plusieurs tortues, et surtout l’instruction« viser une tortue », apportent de nouvelles capacités créatrices aux tortues, en particulier celle de tracer des courbes de poursuite.
Contenu
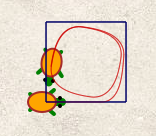
Avec deux tortues, on peut tracer des courbes de poursuite, comme par exemple la courbe du chien : La première tortue est le maître, qui va tout droit à vitesse constante, et la seconde tortue est le chien (!) qui suit son maître. Pour mieux les distinguer, on donne à la tortue-chien un stylo rouge et on la déplace vers le haut avant de démarrer la course :
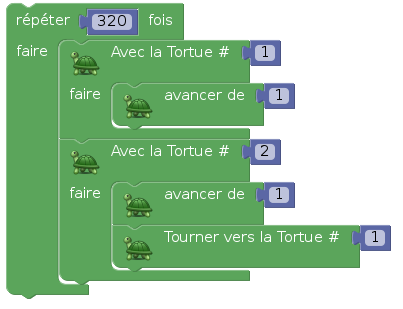
Pour le tracé, on simule du calcul parallèle : Alors que la tortue 1 ne fait qu’avancer, la tortue 2, en plus, se tourne vers la tortue 1 :
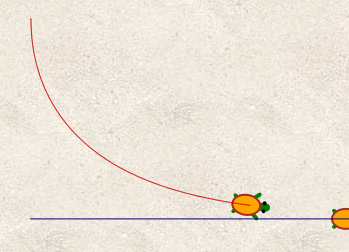
Voici le tracé obtenu :
Pour aller plus loin, on peut aller moins loin (ne pas sortir de l’écran), et faire parcourir à la première tortue, un carré. On peut dessiner un carré en avançant d’un seul pixel à la fois :
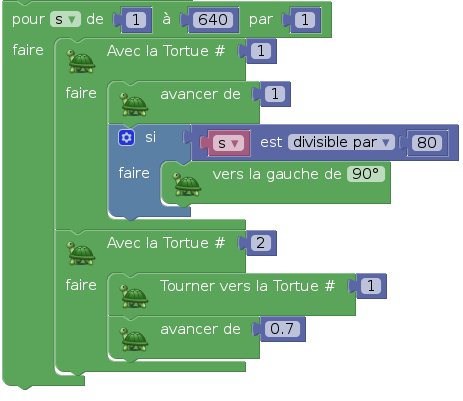
La courbe de poursuite devient vite cyclique, ayant alors la forme d’un carré arrondi :
Avec plus que 2 tortues, on a un essaim, ce qui permet d’aborder le problème des souris (ou des mouches, on a le choix...). Par exemple, on dispose 4 tortues aux sommets d’un carré, et ensuite chaque tortue se dirige vers la suivante. Le plus long, une fois qu’on a créé les 4 tortues, c’est de les personnaliser (leur donner à chacune sa couleur et ses coordonnées initiales). La création des tortues se fait dans une boucle :

Les deux tortues suivantes sont respectivement rouge et verte :
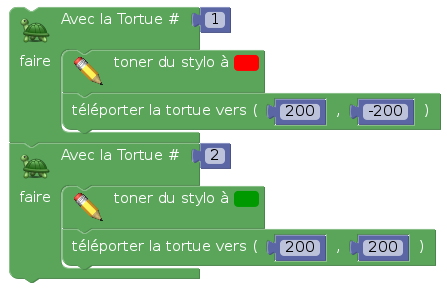
et la dernière est mauve :

Le script lui-même est nettement plus court : On boucle sur ceci :
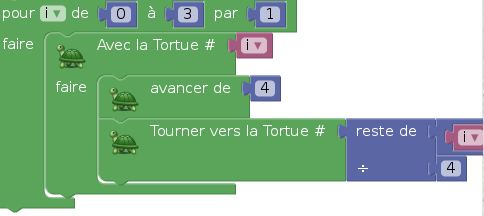
La figure obtenue est symétrique, formée de 4 courbes :

En résumé, la tortue permet de tracer les courbes que l’on connaissait déjà, à savoir les courbes paramètrées, et a le mérite de nous faire découvrir de nouvelles courbes.
Le tortue-centrisme est un courant spirituel qu’il est possible d’épouser. D’autant que la tortue ne va pas très vite.
N’en déplaise aux héliocentriques ordinaires.