Comment on peut rapidement créer une application d’étude de graphes, et ce qu’on peut faire avec.
La figure manipulable en ligne ci-dessous permet, à l’aide de CaRScripts, de créer des graphes (sommets et arêtes), de déplacer les sommets pour rendre les graphes plus lisibles, et d’effectuer quelques analyses sur ces graphes (matrice d’adjacence, test de connexité et d’eulerianisme)
Mode d’emploi
La figure est initialement presque vide (on n’y voit qu’un texte disant qu’il n’y a pas encore de sommets pour le graphe). Pour construire le graphe, on utilise les deux premiers scripts visibles en cliquant en haut à gauche sur l’icône représentant un morceau de parchemin.
Le script AjouterSommet crée un sommet nommé automatiquement et le place au hasard sur la figure ; ce qui n’est pas grave puisqu’on peut déplacer le sommet après coup avec la souris.
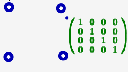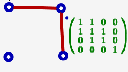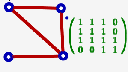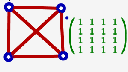
Le script AjouterArete demande la sélection (d’un clic de souris) d’un des sommets du graphe :
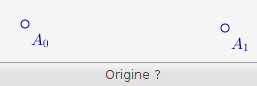
Une fois que le sommet est sélectionné, le script attend le choix d’un autre sommet (en fait ça peut être le même mais dans ce cas, les résultats affichés seront fantaisistes) :
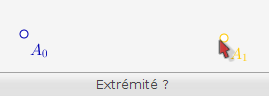
Sitôt qu’on a cliqué sur un second sommet, l’arête apparaît :

La séparation des deux scripts de création de sommets et d’arêtes est néfaste à l’engagement direct (il faut chaque fois resélectionner le script correspondant) mais elle permet de rajouter des sommets alors qu’il y a déjà des arêtes, de déplacer les sommets pendant la construction du graphe, ou après : On reste dans le paradigme de la géométrie dynamique.
Le script adjacence permet d’afficher dans la figure la matrice d’adjacence du graphe. Seulement il pose une question en bas de page :
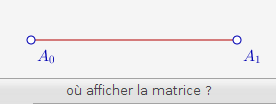
Il suffit alors de cliquer sur un point de la figure (sommet du graphe ou non) voire d’en créer un à la volée (en cliquant sur une zone vide de la figure) pour voir la matrice :

La matrice n’est pas complètement en engagement direct, puisque si l’ajout d’une arête la met automatiquement à jour (voir en exemple l’animation en haut de l’article), ce n’est pas le cas avec l’ajout d’un sommet. De façon générale, on ne peut supprimer un sommet ou une arête qu’en annulant les effets du script [1].
Le script connexité se lance après la construction du graphe, et analyse la connexité du graphe. Idem pour le script euler qui affiche si le graphe est eulérien ou non.
Exemple
Sujet
Voici un exemple d’utilisation, avec un extrait du sujet du Bac ES Pondichery 2012 ; on demande
- Si le graphe ci-dessous est connexe ;
- S’il est eulérien
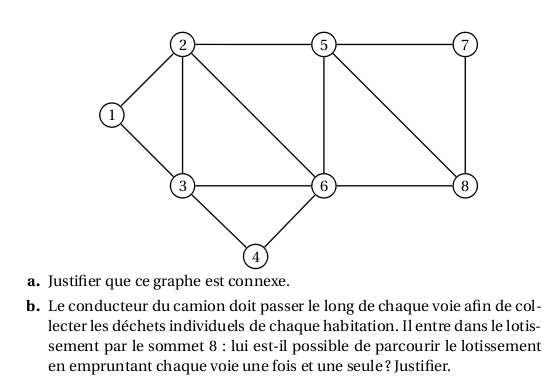
Construction du graphe
On lance donc 8 fois le script AjouterSommet et on place les sommets à peu près comme sur l’énoncé, avec la souris (seulement le sommet numéro 1 s’appelle A0, pas A1) ;
ensuite on lance 13 fois le script AjouterArête et on sélectionne à la souris les extrémités de chaque arête :
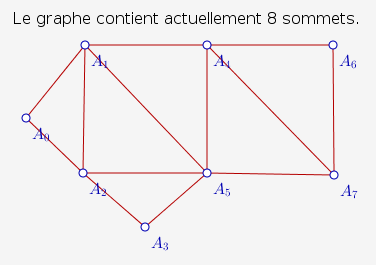
On peut améliorer le placement des sommets après coup, avec la souris, ou en modifiant les coordonnées des sommets dans la fenêtre des propriétés, à l’aide d’un clic droit.
Connexité
Maintenant que la figure est construite, il suffit de lancer le script connexité pour voir apparaître l’affichage suivant :
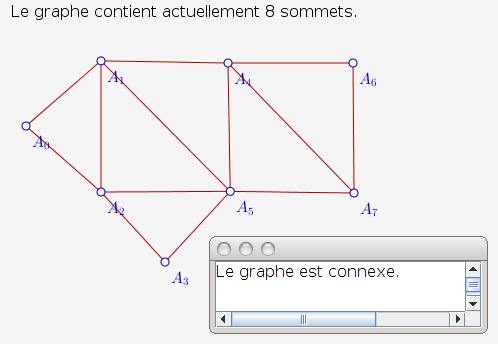
Si le graphe n’avait pas été connexe, l’affichage aurait précisé le nom d’un sommet isolé d’un autre (voir la description des scripts ci-dessous).
Pour voir comment on peut démontrer que le graphe est connexe, on peut faire semblant de modifier le script, pour voir comment il est fait.
Eulérianisme
Même principe, une fois le graphe fini, on lance le script euler pour voir apparaître la réponse tant attendue :
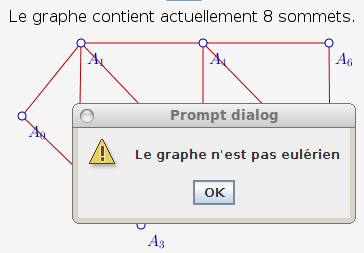
Pour voir comment on peut justifier ce résultat, on peut étudier le script euler soit en ligne, soit ci-dessous.
Voici enfin l’applet CaRMetal :
Les autres onglets vont à deux variantes (incomplètes) :
- Graphes orientés (avec des vecteurs au lieu des segments)
- Graphes pondérés (mais pas orientés)
Pour les graphes orientés et pondérés, voir l’article précédent, partie « matrices ».
Comment ça marche ?
Cette applet n’est pas parfaite [2], mais l’améliorer peut être un bon « projet » en ISN ; à cet effet, voici le contenu des scripts :
Licence
Bien que ce ne soit pas inscrit dans les scripts eux-mêmes (qui contiennent d’ailleurs bien trop peu de commentaires), ceux-ci sont placés sous licence CeCILL, ce qui autorise tout le monde à les étudier, les améliorer et les distribuer aussi largement que possible. Les seules restrictions étant
- que l’auteur des modifications donne son nom
- que la source (MathemaTICE) soit citée lors de la distribution
Sommet
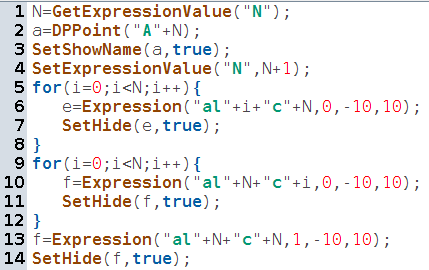
L’argument secret, c’est une « expression » de CaRMetal, cachée quelque part dans la figure, et appelée N. La ligne 1 du script commence par récupérer son contenu dans le script lui-même, sous forme d’une variable JavaScript. Au début (à l’ouverture de la figure), la valeur de N est 0, ce qui fait que le premier point créé (ligne 2) au hasard s’appellera A0 ; par la suite, N est incrémenté (ligne 4) et le prochain sommet s’appellera A1, le suivant A2 etc. ; la ligne 3 du script demande que le nom du sommet soit visible (c’est tout de même mieux pour les graphes).
Les lignes 5 à 8 créent sur la figure des « expressions » invisibles contenant les coefficients de la matrice d’adjacence du graphe, du moins ceux de sa dernière colonne. Le nom d’un de ces coefficients ressemble à al3c2 (pour « a ligne 3 colonne 2 ») ; cette syntaxe est nécessaire pour les autres scripts, qui ont besoin d’accéder à la matrice dans la figure. Ces coefficients sont initialisés à 0 parce qu’il n’y a pas encore d’arête partant du nouveau sommet. Les lignes 9 à 12 font pareil pour la dernière ligne (elles ajoutent une ligne à la matrice qui s’agrandit effectivement lors de l’ajout d’un sommet). Les lignes 13 et 14 créent de même le dernier coefficient de la matrice, initialisé à 1 parce qu’on considère que le dernier sommet est relié à lui-même (c’est un choix) :
Arête
La création d’une arête fait appel à un peu de virtuosité javascriptienne : Le script est inclus (lignes 3 à 11) dans une tentative : On essaye de faire tourner le script, et si ça ne marche pas, un message d’erreur ad hoc est affiché (ligne 14). Merci à l’auteur de CaRMetal de m’avoir montré ça, je sais maintenant à quoi ça peut servir !

Comme on l’a vu ci-dessus, le point à sélectionner comme origine de l’arête est attendu avec un clic et un message d’invite (ligne 3) ; de même pour l’extrémité de l’arête (ligne 4). Les variables origine et extremite contiennent alors des chaînes de caractère : Les noms des points choisis. Ces noms sont de la forme An où n est entier naturel (sinon c’est qu’on a renommé le sommet, ou sélectionné un point qui n’est pas un des sommets du graphe).
Lignes 4 et 5, on crée le nom d’un élément de la matrice, en remplaçant le « A » de l’origine par « al », et le « A » de l’extrémité par « c » puis en assemblant les deux morceaux. Par exemple, si les sommets A2 et A4 ont été sélectionnés dans cet ordre, la variable arete contient le nom al2c4 ; cette entrée de la matrice devient alors égale à 1 (ligne 7) pour indiquer qu’il y a une liaison entre les deux sommets. Lignes 8 à 10, l’entrée de la matrice obtenue en inversant les lignes et colonnes est également mise à 1, pour que la matrice soit symétrique (pour un graphe non orienté, c’est nécessaire).
Enfin, ligne 11, l’arête est dessinée sous la forme d’un segment.
Adjacence
Comme tous les éléments de la matrice d’adjacence sont dans la figure, il suffit de constituer (lignes 1 à 18) une chaîne de caractères en LaTeX pour avoir la matrice :
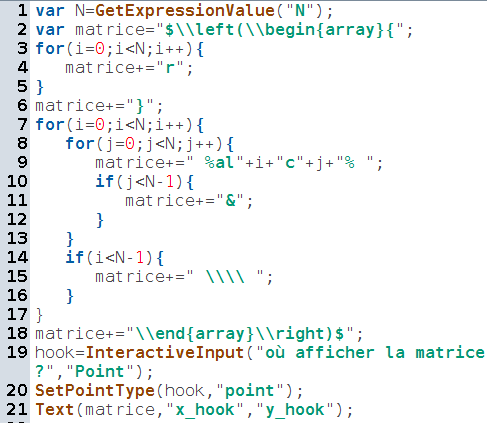
Ligne 19, on demande à l’utilisateur de choisir un point d’accroche où placer la matrice dans la figure ; ligne 20, on rend ce point aussi petit que possible pour qu’il ne gêne pas la lisibilité de la figure. Enfin, ligne 21, on y place la matrice.
Connexité
Pour savoir si le graphe est connexe, on calcule la puissance N ième de la matrice d’adjacence, qui comprend un 0 pour chaque paire de sommets entre lesquels il n’y a pas de chemin. On regarde donc s’il y a un zéro dans la matrice.
Pour commencer, on doit donc placer une fonction JavaScript de produit de matrices A et B, qu’on va appeler N fois pour calculer la puissance de la matrice d’adjacence (lignes 3 à 16) :

Ensuite, lignes 18 à 24, on crée une matrice en JavaScript, où on case les coefficients de la matrice lus dans la figure.

Ligne 25, on crée une matrice mp que l’on remplace par son produit par la matrice du graphe (ligne 27). N fois, donc mieux que Chuck Norris [3]
À la ligne 28, mp contient donc la puissance Nème de la matrice d’adjacence. Puis on initialise l’affirmation connexe comme vraie (a priori, le graphe est connexe, jusqu’à plus ample informé). Lignes 29 à 37, on parcourt la matrice puissance à la recherche d’un indice de non connexité (un coefficient nul) ; si on en trouve un, on décrète que le graphe n’est pas connexe et on enregistre dans la variable s2 une information expliquant pourquoi.
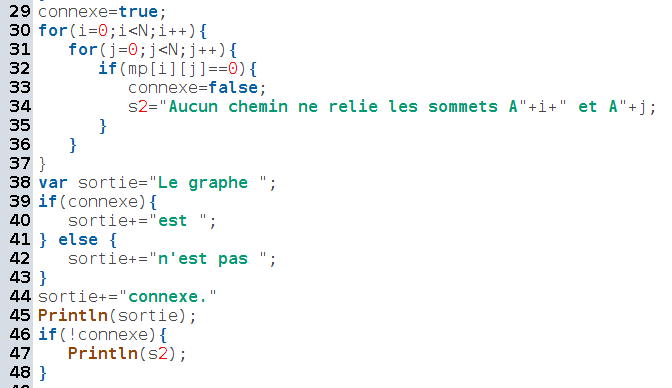
Lignes 38 à 44, on constitue un diagnostic, sous forme d’une phrase affirmative ou négative selon que le graphe est connexe ou non. Ligne 45, on affiche ce diagnostic et le cas échéant, l’information supplémentaire s2.
Euler
Pour voir si on a affaire à un graphe eulérien, on utilise le théorème d’Euler : On vérifie si le degré de chaque sommet est pair [4].
Pour commencer, on a besoin de récupérer comme précédemment, les expressions de la figure, dans un tableau JavaScript (la matrice). Lignes 1 à 8 :
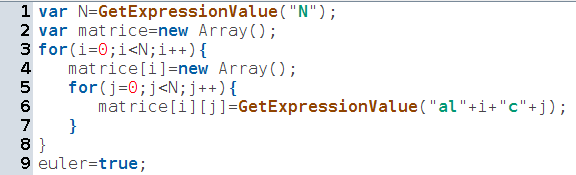
Ligne 9, on décrète par pur optimisme que oui, le graphe est eulérien. L’algorithme utilisé consiste en effet à chercher un sommet de degré impair qui invalidera cette hypothèse. On peut parler de démonstration par un contre-exemple... La boucle qui commence à la ligne 10 parcourt donc les sommets du graphe, et pour chacun d’eux, calcule son degré en additionnant 1 chaque fois qu’on rencontre une arête allant de (lignes 12 à 16), ou vers (lignes 17 à 21), ce sommet.
Comme la matrice est symétrique, on divise le degré par deux (ligne 22) parce qu’on a compté chaque arête deux fois ; puis on soustrait le sommet lui-même (ligne 23) qui ne compte pas.

Enfin on teste la parité du degré de ce sommet (ligne 24) et si le sommet empêche le graphe d’être eulérien, on décrète le graphe comme définitivement non eulérien (ligne 25).
Les lignes 28 à 34 élaborent un diagnostic selon que le graphe est, ou non, eulérien :

La ligne 35 affiche ce diagnostic dans un « po-up ».
Pondération
L’éventuel lecteur qui aura eu le courage de lire jusqu’ici, est invité à regarder les scripts de l’onglet « pondéré » pour voir comment CaRMetal permet de facilement afficher le poids d’une arête.
La concurrence
Certes, il existe déjà de très bons logiciels accomplissant ce genre de tâches [5]. En voici une liste non exhaustive :
- GeoGebra, qui, depuis la version 4.0, peut rechercher le plus court chemin sur un graphe pondéré complet (sauf que les poids sont juste les distances) ; avec ReprésentantCommerce suivi de la liste des noms des sommets du graphe.
- Jung, une bibliothèque de graphes en Java qui est d’ailleurs une composante de la suite mathpiper (aux côtés de GeoGebra) ;
- GraphViz, logiciel de dessin de graphes
- GraphThing
- Et pour finir le jeu Planarity), aussi addictif qu’indispensable...