par groupe Lycée Professionnel – IREM d’Aix-Marseille, Pascal Padilla
Le groupe Lycée Professionnel de l’Irem de Marseille est composé d’un didacticien et d’une dizaine d’enseignants. Travaillant en lycée professionnel, nous enseignons les mathématiques à nos élèves de CAP et de Bac Pro. Cette année, nous avons beaucoup travaillé pour la diffusion de nos travaux. La mise à jour de notre site internet en est la partie la plus visible.
- 02
Vous pourrez trouver sur ce site des vidéos pour les enseignants (des tutoriels ou des compléments disciplinaires) ainsi que des modules clés en main d’Enseignement Général Lié à la Spécialité.
En outre, et c’est l’objet de cet article, vous pourrez y trouver toute une batterie de travaux pratiques assistés par ordinateurs permettant d’aborder des notions mathématiques grâce à l’enseignement des sciences.
Expérimentation Assistée par Ordinateur (ExAO)
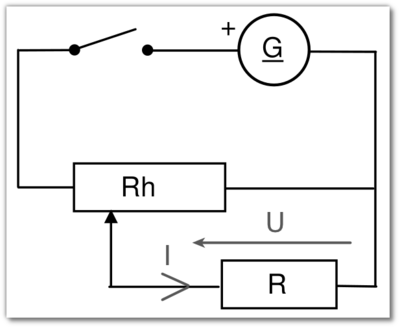
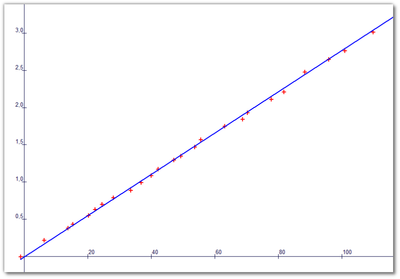
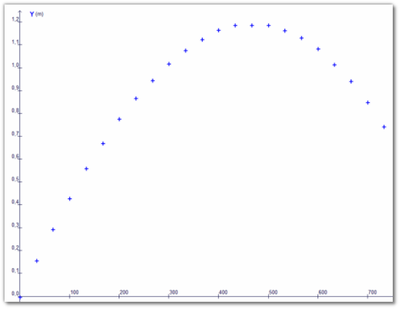
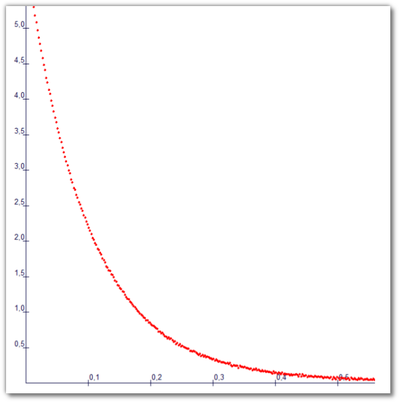
Pour toutes les classes de CAP et pour les classes de baccalauréat professionnel de type industriel, nous enseignons aussi les sciences-physiques et chimiques. Nous sommes donc bivalents. Cette bivalence nous permet d’aborder les notions mathématiques de façon parfois originale. Ainsi, un des axes de travail du groupe ces dernières années, a été d’utiliser les sciences pour aborder et traiter des notions mathématiques. Dans cette optique, nous avons développé une dizaine de séances de sciences. Ces travaux pratiques d’acoustique, de mécanique, de thermodynamique et d’électricité ont été pour nous autant de thèmes nous permettant d’aborder les statistiques, les suites arithmétiques, la géométrie, les fonctions linéaires, affines, carrées et exponentielles, les nombres et les fonctions dérivées, le sens de variation ou encore les fonctions définies par une aire.
D’autres exemples de TP
Dans la suite de l’article, nous décrivons rapidement quelques uns de nos TP liant explicitement les mathématiques et l’expérimentation assistée par ordinateur.
Pour conclure
À travers ces exemples, nous avons voulu vous montrer une partie du travail effectué par le groupe Lycée Professionnel de l’Irem de Marseille. Ce travail a été diffusé auprès d’une quinzaine de collègues par le biais du plan académique de formation durant l’année scolaire 2009/2010.
L’enseignant bivalent, lorsqu’il dispense les deux matières, fait nécessairement le lien entre les mathématiques et les sciences. C’est d’ailleurs depuis des années une recommandation explicite dans nos programmes. Par contre, l’originalité de notre démarche a été d’utiliser le matériel de sciences pour enseigner les mathématiques. Le laboratoire de sciences physiques et chimiques, équipé de consoles d’acquisition permettant un grand nombre de relevés, que ce soit sur des temps très courts ou au contraire très longs, est devenu un lieu privilégié ou les mathématiques ont pu donner du sens aux sciences.