Introduction

Dans l’enseignement de la notion de tangence, la droite tangente est la toute première notion faisant objet d’étude. Cependant, plusieurs recherches à l’instar de (Kuntz, 1997) montrent que le lycéen de classe de première rencontre encore plusieurs difficultés pour appréhender cette notion. Nous allons en particulier nous attarder sur la difficulté pour certains lycéens à reconnaitre la droite tangente lorsqu’elle se trouve dans certaines configurations. Notamment, lorsqu’elle traverse sa courbe associée sans la recouper. Nous cherchons à lui proposer un outil, lui permettant de reconnaitre dans l’environnement de géométrie dynamique la droite tangente dans les les différentes configurations évoquées.
Nous allons aussi l’inviter à construire une argumentation prenant appui sur le même outil et visant à proposer une explication, permettant de justifier (et non de démontrer) pourquoi une droite tangente peut ne pas recouper sa courbe associée. Pour ce faire nous lui donnons des occasions d’acquérir ces connaissances sous la forme opératoire. Visant ainsi, la conceptualisation dans l’action sur les notions mathématiques en jeu (Vergnaud, 2001, 1999). Le nombre dérivé est une notion intéressante pour faire travailler les lycéens sur la notion de tangence dans le cadre de l’analyse mathématique. Cependant, la droite tangente est avant tout un objet géométrique. Pour cette raison, il est davantage question dans cette étude de lui proposer un outil, lui permettant de penser à la droite tangente dans le cadre géométrique.

 1. Les connaissances antérieures des participants sur la notion de tangence

Les participants se sont appropriés en cours ordinaires d’autres points de vue de la droite tangente, enseignés en classe de première scientifique. Et notamment le point de vue de la dérivation. Ils savent le mobiliser pour produire une équation algébrique de la droite tangente à la courbe d’une fonction. Dans le registre algébrique, les participants sont capables de montrer qu’une droite tangente ne recoupe pas sa courbe associée ou de démontrer qu’une droite tangente recoupe sa courbe associée. Cependant, même après les démonstrations, les participants posent, entre autres, la question suivante : pourquoi la droite tangente ne recoupe pas sa courbe associée dans certains cas et la recoupe dans d’autre cas ?
Cette étude vise à proposer des éléments de réponses à cette question dans l’environnement de géométrie dynamique. En revanche la notion d’ordre de multiplicité du point de tangence n’est pas encore connue. Elle fera partie des objets d’enseignement pendant cette séance.

 2. Les points de la géométrie dynamique

La géométrie dynamique mêle géométrie et mouvement. La littérature distingue trois principaux points de cet environnement (Restrepo, 2008). Le point libre, le point lié sur l’objet ou le point sur l’objet et le point non attrapable. Ils se caractérisent par la technique mise en œuvre pour les déplacer. Restrepo (2008) propose une caractérisation des dits points lorsqu’elle dit :

Le point libre qui peut se déplacer partout ; le point sur objet, qui ne se déplace que sur l’objet (segment, droite, cercle) ; le point non attrapable, qui ne peut pas être attrapé et déplacé directement, mais qui dépend d’un autre point (point d’intersection, milieu). Ces trois types de points définissent des instruments déplacement caractérisés par des usages du déplacement (p.42)

L’auteure précise les déplacements associés à chaque type de point :

• Déplacement libre : déplacer un point libre partout dans l’écran.
• Déplacement contraint ou limité (bound dragging) : déplacer des points qui se trouvent sur un objet et qui ne peuvent être déplacés que sur cet objet (courbe d’une fonction).
• Déplacement indirect : les points non attrapables, ne pouvant pas être déplacés directement, ils ne peuvent être déplacés que par l’intermédiaire d’un autre en attrapant et déplaçant des points « sources » à partir desquels sont définis les points non attrapables. Par exemple, le milieu I du segment [AB], ne peut pas être déplacé directement, mais en déplaçant les points A ou B, I sera déplacé de manière indirecte.

À ces trois catégories de points, il nous semble nécessaire d’en ajouter une quatrième. Il s’agit des points fixes sur l’objet. Ils ne sont pas déplaçables et restent toujours fixes sur l’objet. Ce type de point est lié à la fonctionnalité « algébrique » de GeoGebra mais ne relève pas d’une définition géométrique stricte. Par exemple, dans l’environnement GeoGebra en construisant un point A avec la syntaxe suivante < A=(1,f(2)) > on obtient un point fixe sur la courbe de la fonction. Nous utilisons cette syntaxe pour construire le futur point de tangence A. Afin, qu’il ne bouge pas au cours du rapprochement du point B sur la courbe, vers le futur point de tangence A.

 3. Droite sécante stricte, point d’intersection simple, relation de « sécance stricte » et valeur de (p)

Nous allons proposer une définition de point d’intersection simple en prenant appui sur la notion de limite. Les participants à cette étude ont travaillé sur la notion de limite en cours ordinaire. Considérons une fonction $f$ à une variable réelle continue en un réel $x_0$. Le réel $x_0$ est une racine simple de la fonction $f$, si et seulement si, $f(x_0)=0$ et $\lim_{x \rightarrow x_{0}}\dfrac{f(x)}{x-x_0}\neq 0$.

Considérons un réel $x_0$, une fonction $f$ et $g$ une droite sécante à la courbe de la fonction $f$, passant par le point A d’abscisse $x_0$. la fonction définie par : $p : x\longmapsto f(x)-g(x)$. Si Le réel $x_0$ est une racine simple de la fonction $p$, alors l’interprétation géométrique que nous faisons est la suivante : à la position du point $A\left(\begin{array}{c} x_{0} \\ f\left(x_{0}\right)\end{array}\right)$, la droite sécante et la courbe forment une intersection simple. Prenons un exemple pour illustrer notre propos.

 3.1 Cas d’une fonction numérique à une variable

Considérons la fonction définie par : $f : x\longmapsto x^{3}+4x^{2}-5$ la fonction $g : x\longmapsto x-1$ le réel $x_0=1$, la fonction $p : x\longmapsto f(x)-g(x)=(x-1)(x+2)(x+3)$. Le réel 1 est une racine simple du polynôme $p$ ou le réel 1 est une racine de $p$ donc l’ordre de multiplicité est égal à 1, car $p(1)=0$ et $\lim_{x \rightarrow 1}\dfrac{p(x)}{x-1}\neq 0$ . L’interprétation géométrique que nous faisons est la suivante : à la position du point A d’abscisse 1, la courbe (c) et la droite (g) forment une intersection simple, ou une intersection dont l’ordre de multiplicité est égal à 1. Nous disons alors que le point A d’abscisse 1 est un point d’intersection simple ou que le point A d’abscisse 1 est un point d’intersection dont l’ordre de multiplicité est égal 1. Pour les mêmes raisons nous disons que les points B d’abscisse −2 et C d’abscisse −3, sont des points d’intersections simples entre la courbe (c) et la droite g. Dans le cadre de cette étude, nous appelons alors droite sécante stricte à une courbe (c), toute droite formant avec cette courbe uniquement des points d’intersections simples. Ceci, dans le but de lever toute ambigüité entre une droite sécante et une droite tangente.
Par ailleurs le nombre de racines simples du polynôme est égal à trois. L’interprétation géométrique que nous faisons est la suivante : le plus grand nombre de points d’intersections simples que forment la courbe et la droite (g) est égale à trois. Dans la littérature nous n’avons pas trouvé de concept pour désigner une relation entre deux objets géométriques liés uniquement par des points d’intersections simples, comme par exemple les points A, B et C qui lient la courbe (c) et la droite (g). Nous proposons de nommer cette relation par « relation de sécance stricte ».

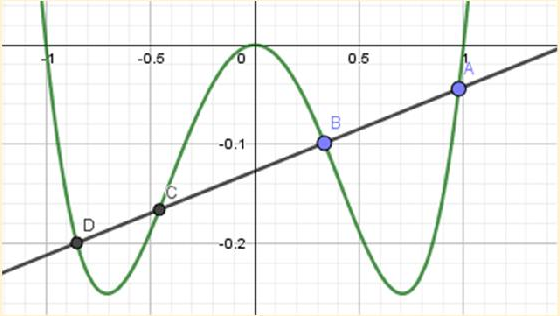
 3.2 Illustration graphique des points d’intersections simples d’une relation de sécance stricte

 4. Points convergents, ordre de multiplicité du point de tangence et relation de tangence

Nous allons proposer une définition de point convergent à partir de la notion de point non attrapable, de point sur la courbe et de point fixe sur la courbe de l’environnement de géométrie dynamique. Il existe des techniques comme celle décrite ci-dessous, permettent de transformer des relations de sécantes strictes en relations de tangence dans certains environnements de géométrie dynamique. Lors du passage de la sécante à sa position limite certains représentants des points d’intersection de la relation de sécante stricte partent se superposer à l’écran à la position du point fixe. Dans certains cas, des non attrapables en font partie. Nous proposons de nommer ces points qui viennent se superposer à la position du point fixe, des « points convergents  ». Et le point fixe est pris en compte dans le décompte des points convergents. Les points convergents sont alors des points dont les représentants se superposent à l’écran, après le passage de la sécante à sa position limite, pour former une représentation du point de tangence. Ainsi, le nombre de points convergents est égal à l’ordre de multiplicité du point de tangence. La courbe et sa droite tangente sont alors liées au point de tangence par des points convergents dont les représentants sont en position de superposition à l’écran. Nous proposons d’appeler ce lien entre les deux courbes « relation de tangence ». Le terme relation vise à attirer l’attention du lecteur sur le caractère symétrique de ce contact particulier entre les deux objets géométriques.
Notre hypothèse est que, les lycéens arriveront à établir que, le nombre de points convergents, est égale l’ordre de multiplicité de l’abscisse $x_{A}$ du point de tangence lorsqu’elle est racine de la fonction $p : x \longmapsto f(x)-T(x)$ .Où $T$ désigne la droite tangente en A à la courbe de la fonction $f$. Et que ce travail va leur permettre de s’approprier la définition suivante relative à la notion de droite tangente : une droite et une courbe sont liées par une relation de tangence en un point A, si et seulement si, elles forment à la position du point A une intersection dont l’ordre de multiplicité est supérieur ou égal à deux.

Nous faisons également l’hypothèse que le sens géométrique et dynamique construit sur le concept d’ordre de multiplicité du point de tangence, va aider le participant à construire une argumentation satisfaisante du point de vue de la géométrie dynamique et visant à expliquer pourquoi la droite tangente peut, entre autres, ne pas recouper sa courbe associée.
Par ailleurs, cette notion d’ordre de multiplicité du point de tangence a été évoquée par nombre de chercheurs à l’instar de (Gantois, 2012 ; Artigue, 1989). Artigue parle du nombre de points confondus  : « une droite est tangente à une courbe si elle coupe cette courbe en deux points confondus » (1989, p.275). La chercheure précise que ce point de vue de la droite tangente ne nécessite pas l’intervention explicite du calcul différentiel. Gantois (2012) fait plutôt référence à une intersection double lorsqu’il dit que : « la deuxième conception est un progrès dans la mesure où elle s’attarde à vérifier qu’il n’a pas d’autre intersection dans un voisinage du point tangence » (p.132). Nous resterons davantage proche de Gantois et parlerons de point d’intersection double, voire de point d’intersection multiple. Puisque notre étude prend appui sur un environnement de géométrie dynamique, nous parlerons aussi en termes de représentants des points qui se superposent à la position du futur point de tangence. Mettant ainsi à profit la possibilité de visualiser la superposition de représentants des points dans ce milieu.

 4.1 Illustration graphique des points convergents dont les représentants sont en position de superposition à l’écran

 4.2 Domaine de validité des conditions suffisantes pour qu’une droite tangente ne traverse pas sa courbe associée ou ne la recoupe pas

Les points A, B, C et D de la figure (1) ci-dessus sont des points d’intersections simples qui lient la courbe (c) et la droite sécante stricte. Le plus grand nombre (p) de points d’intersections simples que peut former une droite sécante à la courbe et passant par le point A est égal à quatre. Car, le degré du polynôme est quatre. Cette relation de sécance stricte est alors transformable en relation de tangence, avec la possibilité de déterminer graphiquement la valeur exacte de l’ordre de multiplicité du point de tangence (m). Cependant, pour certaines courbes de fonctions, (p) peut prendre une valeur infinie, comme par exemple la fonction définie par $f(x)=\sin\left(\frac{1}{x}\right)$, avec comme point A le point d’abscisse $\frac{2}{\pi}$. Dans l’environnement GeoGebra, il est très difficile de mettre en œuvre la technique sous-décrite pour transformer la relation de sécance stricte en relation de tangence. En revanche, la technique qui consiste à considérer un unique point sur la courbe et à faire coïncider à l’écran son représentant avec celui du futur point de tangence, pour obtenir un représentant de la droite tangente (Nguembou-Nana, 2022) permet de construire la droite tangente en un point d’une courbe, même lorsque la valeur de (p) est infinie. Un inconvénient avec cette approche est qu’elle ne permet pas de déterminer graphiquement avec exactitude la valeur de l’ordre de multiplicité du point de tangence. Même dans les cas des courbes où (p) prend une valeur finie, comme par exemple celui de la fonction définie $f(x)=\frac{x^{3}}{3}-x^{2}$.
Une conséquence éventuelle sur l’apprentissage de la notion de point tangence est qu’elle peut laisser croire à l’apprenant que l’ordre de multiplicité du point de tangence est toujours égal à deux. Pourtant, ce concept peut être très intéressant dans l’apprentissage de la notion de meilleure approximation circulaire. Dès lors, plus l’ordre de multiplicité du point de tangence liant un cercle et une courbe est élevé, plus le contact entre le cercle et la courbe est fort. C’est ainsi par exemple, que l’on arrive à regarder le cercle osculateur, comme la meilleure approximation circulaire de la courbe au voisinage du point de tangence. Car l’ordre de multiplicité du point de tangence liant le cercle osculateur et la courbe est le plus élevé parmi les cercles tangents à la même courbe au même point de tangence.
Ainsi, nous faisons travailler les apprenants sur le cas de fonctions à valeur de (p) finie. Dans le but de leur donner des occasions de mettre en relation la valeur de (p) et la valeur exacte de (m) pour chercher, entre autres, une condition suffisante pour qu’une droite tangente ne recoupe pas sa courbe associée. Cette condition sera alors valide ou n’aura de sens que dans le cas des courbes de fonctions pour lesquelles (p) prend une valeur finie.
Comme le soutient (Balacheff, 1995) l’apprentissage est un processus évolutif. Le chercheur le dit en ces propres termes : « l’apprentissage est un processus permettant de passer d’une conception à une autre » (1985, p.17). Ainsi, cette étude voudrait, entre autres, donner aux élèves des outils susceptibles de les aider à proposer une condition suffisante pour laquelle la droite tangente ne recoupe pas sa coupe associée dans le cas de courbe à valeur de (p) finie. Avec espoir que dans les niveaux de classes supérieures, de nouveaux outils leur seront proposés pour le cas de fonction à valeur de (p) infinie. C’est entre autres pourquoi, dès le titre, nous parlons de conditions suffisantes (mais non nécessaires).

 5. Problématisation de l’objet de recherche

 5.1 La conception d’Unique Point d’intersection (C1) : un obstacle à l’apprentissage de la notion de la droite tangente telle que proposée par la dérivation.

Une pensée gouvernée par la conception (C1) voudrait que le sujet regarde la droite tangente comme une droite ayant un unique point commun avec la courbe et se situe d’un seul côté par rapport à celle-ci (Artigue, 1989). Ces connaissances construites par le sujet dans le cadre du cercle y sont valides. Mais ne le sont plus, par exemple pour les cubiques, dans le cadre fonctionnel. Par suite, elles pourraient devenir une source de difficultés pour, l’apprentissage du concept de droite tangente dans ce nouveau cadre. En effet, les travaux antérieurs dont ceux de (Dufour, 2019 ; Delgadillo et al., 2016 ; Balhan et al., 2015) sont unanimes sur le fait que, dans le registre graphique, la structure de contrôle de la conception (C1) ne permet pas à certains lycéens de reconnaitre la droite tangente lorsque celle-ci traverse la courbe associée au point d’inflexion, ou lorsqu’elle la recoupe. Car, ces configurations sont absentes dans le cadre du cercle, où les connaissances initiales sur ce concept ont été construites. Ils soutiennent alors que le lycéen a tendance à transposer à la droite tangente à la courbe d’une fonction, les connaissances construites sur la droite tangente au cercle. Par suite, la droite tangente à la courbe d’une fonction devient pour le lycéen la droite qui frôle ou coupe ou touche la courbe en un unique point (Delgadillo et al., 2016 ; Tall, 1985) et se situe d’un seul côté par rapport à la courbe. Ces connaissances transposées par le sujet dans le cadre fonctionnel y sont en général erronées. Elles ne permettent souvent pas au lycéen de reconnaitre la droite tangente en un point à la courbe dans certaines configurations.

Dufour (2019) explique que : « certains chercheurs […] observent que les étudiants arrivant dans les cours de calcul différentiel ont déjà abordé au secondaire le concept de tangente, et ce, dans le contexte de la tangente au cercle. » (p.9). La chercheure ajoute que : « ce contexte amène une conception de la tangente restreinte à l’image d’une droite qui « touche » un cercle à un point » (p.9). Plus loin l’auteure soulève la difficulté que pourrait engendrer cette conception initiale : « quand la tangente en point traverse le graphique en un autre point […] l’élève ayant une vision globale de la tangente peut ne pas accepter la droite étudiée comme tangente » (p.10). De plus, la chercheure évoque un autre cas : « Un autre exemple perturbant est la tangente en un point d’inflexion […] l’élève a tendance à ne pas accepter cette droite comme étant une tangente (Biza et Zachariades, 2010 cités par Dufour, 2019) » (p.10).
La méconnaissance de la droite tangente dans les configurations sus-décrites par le lycéen, semble être l’argument principal qui permet à la recherche de soutenir que la conception (C1) pourrait s’opposer [1] à l’apprentissage de la notion de droite tangente, telle que proposée par la dérivation. Il s’agit alors d’un obstacle didactique qui devrait être levé en donnant une définition rigoureuse de la tangente à une courbe.

 5.2 L’absence de perspectives locales : une source de difficulté à l’apprentissage de la notion de droite tangente

Une raison complémentaire, pour expliquer pourquoi le lycéen peut ne pas reconnaitre la droite dans les configurations sus-décrites, est proposée par la recherche. La notion de vision locale ou de perspective locale est alors mise en avant. Autrement dit, les liens qu’entretiennent la droite tangente et la courbe associée au voisinage du point de tangence. De nombreuses recherches dont celles de (Panero, 2018 ; Vivier, 2010 ; Maschietto, 2004, 2003, 2002 ; Tall, 1985) s’inscrivent dans un paradigme qui voudrait qu’une droite tangente soit pensée comme un objet global, dont la compréhension est locale. Ainsi, les propriétés locales seraient essentielles pour la reconnaissance d’une droite tangente. Pourtant, les travaux de certain(e)s chercheur(e)s à l’instar de (Vandebrouck, 2011) ont décrié avec force l’absence des perspectives locales sur les fonctions chez les étudiants en début d’université. Les résultats de ces travaux convergent avec ceux de plusieurs chercheurs, à l’instar de (Delgadillo et al., 2016), lorsque ceux-ci ont travaillé sur les conceptions des étudiants en début d’université, en se focalisant sur la notion de droite tangente. Ainsi, des chercheurs en didactique des mathématiques (Dufour, 2019 ; Alory et al., 2015) soutiennent que l’absence des perspectives locales chez les lycéens pourrait expliquer pourquoi ces derniers ont des difficultés à reconnaitre la droite tangente lorsqu’elle traverse sa courbe associée au point d’inflexion ou lorsque qu’elle la recoupe.

 5.3 La conception algébrique : un obstacle à surmonter pour l’apprentissage de la notion de tangence. 

Une pensée gouvernée par la conception Algébrique [2]voudrait que le sujet regarde la droite tangente au point $\left(a,f(a)\right)$ à la courbe d’une fonction numérique $f$, comme une droite passant par ledit point et dont la pente est le nombre dérivé (Artigue, 1989). Ces connaissances construites par le sujet dans le cadre fonctionnel y sont valides, mais ne sont pas utilisables dans le cadre du cercle. Notamment lorsque le cercle n’est pas défini fonctionnellement. Ainsi, la conception Algébrique peut générer un conflit cognitif chez un lycéen, dès lors qu’il faudrait que celui-ci fasse coexister les conceptions (C1) et (C2). Car, la structure de contrôle de la conception (C2) permet au sujet de reconnaitre et d’accepter qu’il s’agit d’une droite tangente lorsque celle-ci traverse sa courbe associée, alors que la structure de contrôle de la conception (C1) invite le même sujet à déclarer qu’il ne s’agit pas d’une droite tangente.
Le sujet pourrait alors être tenté de rejeter l’une des structures de contrôle. Ainsi, la gestion de la coexistence des conceptions Algébrique et celle d’Unique Point d’Intersection par le lycéen, pourrait devenir une source de difficultés pour l’apprentissage de la notion de droite tangente. D’autant plus que, les travaux de (Balhan et al., 2015) soutiennent que le changement de conceptions est très peu pris en compte dans les manuels scolaires ainsi que, dans les pratiques de classe en général. Les travaux de ces chercheurs convergent avec ceux de (Alory et al., 2015), lorsque ceux-ci soutiennent que les différentes notions de tangente cristallisent plusieurs difficultés à surmonter par l’apprenant. Parmi ces difficultés les chercheurs mettent le curseur sur le fait que : « En première, les manuels ne relient guère la notion de tangente avec la conception préalable des élèves, qui peut pourtant s’avérer soit un obstacle, soit un point d’appui » (p.2).
Les résultats des chercheurs évoqués sont encore d’actualité. En effet, dans nos manuels scolaires en vigueur, à l’instar de la collection CIAM, dans lequel nous constatons que le travail sur la dérivation ne prend pas en considération la conception (C1). Nullle part dans ce documentne figurent des tâches visant à mettre en lien le travail fait sur la droite tangente dans le cadre du cercle et le travail fait sur le même objet d’étude dans le cadre fonctionnel. Le programme officiel de classe de première ne donne aucune recommandation à l’enseignant sur la gestion du passage du cadre du cercle au cadre fonctionnel, en ce qui concerne l’enseignement des notions de tangences. Ainsi, le lycéen de classe de première pourrait se retrouver tout seul pour gérer la coexistence de la conception Algébrique et de la conception d’Unique Point d’Intersection.

 6. Une technique opérationnelle, permettant de transformer une relation de sécance stricte en relation de tangence, de sorte que l’on puisse déterminer la valeur exacte de l’ordre de multiplicité du point de tangence (m)

Les objets mathématiques sont des objets abstraits. Les mathématiciens travaillent alors avec et sur certains de leurs représentants (Duval, 1994). Dans l’environnement GeoGebra les représentants des objets mathématiques permettent de construire un représentant du point de tangence et par suite, un représentant de la droite tangente. Dès lors, nous admettons que des points sont confondus, si leurs représentants se confondent à l’écran ou se superposent à l’écran. Aussi une relation de tangence est reconnue dans cet environnement, par la visualisation des points convergents en position de superposition à l’écran.
Nguembou-Nana (2022) a proposé une technique opérationnelle dans l’environnement GeoGebra et permettant construire de façon dynamique un représentant d’une droite tangente à une courbe de fonction ou à une conique. En faisant coïncider le représentant d’un point sur la courbe avec celui du point fixe. Cette technique peut alors laisser sous-entendre que l’ordre de multiplicité de tout point de tangence est égal à deux. Nous allons adapter cette technique pour construire dans cet l’environnement, un représentant du point de tangence de sorte que l’on détermine graphiquement la valeur exacte l’ordre de multiplicité du point de tangence.

 6.1 Construction d’une relation de sécance transformable en relation de tangence

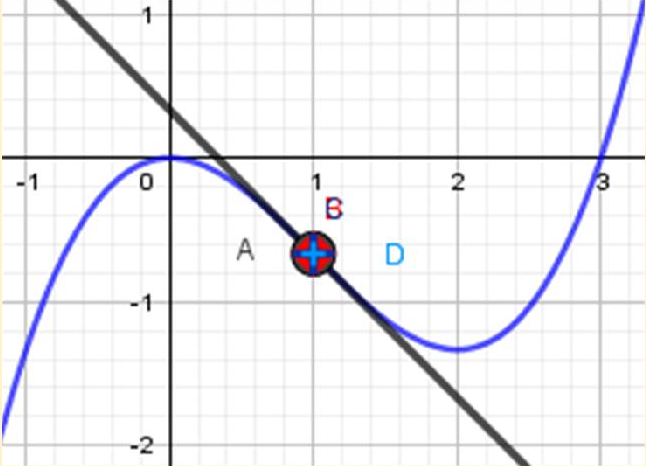
La technique consiste à construire un point A fixe sur la courbe (le futur point de tangence), un point B sur la courbe, la droite sécante (AB) de sorte que celle-ci forme avec la courbe le plus grand nombre (p) de points d’intersections simples (lorsque cela est possible). Matérialiser ces points d’intersection simples en des points non attrapables, grâce à la fonctionnalité « intersection ». Ainsi, on obtient une relation de sécance stricte, transformable en relation de tangence dans l’environnement GeoGebra (voir la fig-3 ci-dessous).

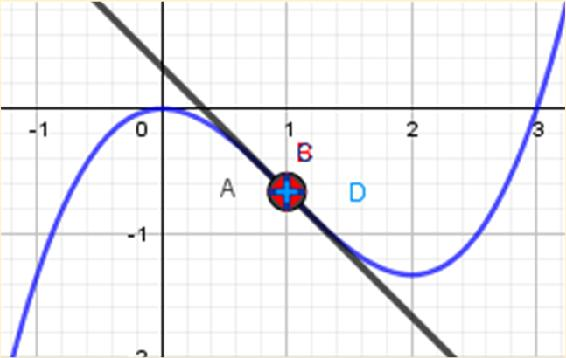
 6.2 Rapprochement inépuisable entre la sécante et la tangente obtenu par la coordination des fonctionnalités déplacement et zoom

La transformation de la relation de sécance en relation de tangence débute avec le rapprochement du représentant du point B à proximité de celui du point A. Ce déplacement implique le déplacement des représentants des points non attrapables, tantôt vers le point A, tantôt vers la direction opposée au point A. L’usage de la fonctionnalité déplacement toute seule fait disparaitre la droite à l’écran. Pour surmonter cette difficulté spécifique à cet environnement informatique, on peut convoquer la fonctionnalité zoom. On fait alors des zooms entre les représentants des points A et B. Ces actions font agrandir à l’écran la représentation de la distance entre le représentant du point A et le représentant du point B. La fonctionnalité déplacement permet à nouveau de rapprocher le point B sur la courbe à proximité du point fixe sur la courbe A. On peut réitérer les mêmes opérations jusqu’à ce que la figure atteigne le point de saturation.

 6.3 Le point de saturation

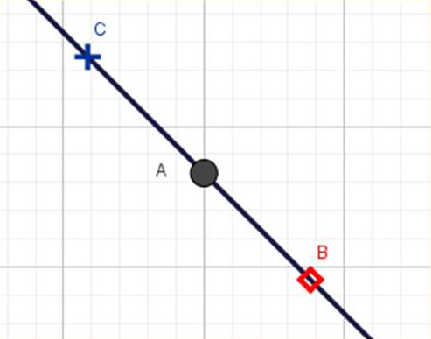
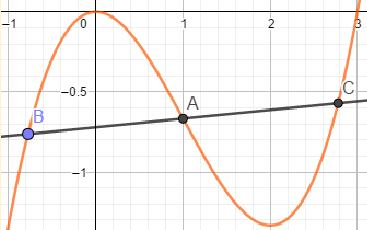
Lors du rapprochement du représentant d’un point B sur la courbe vers le représentant du point fixe A, en mettant en œuvre la technique décrite ci-dessus, survient un moment où les coordonnées analytiques des points A et B sont identiques à l’écran dans la fenêtre algébrique, grâce à la possibilité pour le logiciel des faire des arrondis, pour des points très proches. Si tel n’est pas encore le cas, la poursuite du rapprochement du point sur la courbe vers le point fixe sur la courbe, à l’aide de la coordination des fonctionnalités zoom et déplacement, permet à un moment donné au logiciel de procéder auxdits arrondis, dans la fenêtre algèbre. Avec les représentants des points A et B bien distincts à l’écran dans la fenêtre géométrie. Mais aussi, le représentant d’une portion de la courbe et le représentant d’une portion de la sécante apparaissent à l’écran comme confondus et formant une image semblable à un segment de droite (voir la fig-4 ci-dessous). Nous admettons alors que le rapprochement a permis à la figure d’atteindre son point de saturation.
Selon la nature de la courbe, trois scénarios se présentent. Un point non attrapable (lorsqu’il existe) peut converger vers le futur point de tangence A ou vers un autre point de la courbe (point par lequel la droite recoupe la courbe) ou disparaitre sur la courbe (point tombant).

 6.4 Le passage de la droite sécante à sa position limite : les zooms inverses

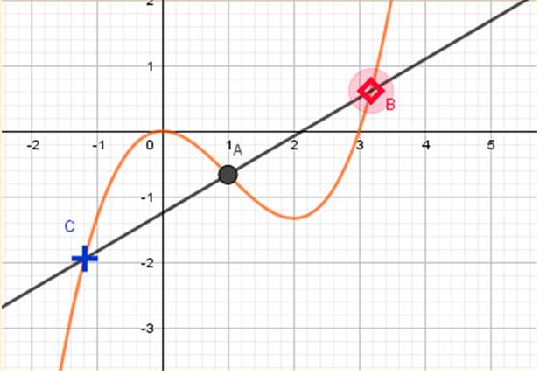
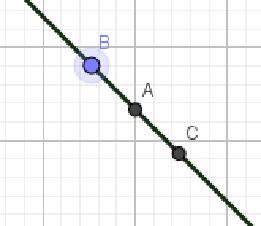
À partir du point de saturation, on peut faire coïncider à l’écran les représentants des points A et B et des éventuels points non attrapables, à l’aide des zooms inverses. On obtient ainsi une relation de tangence, avec la possibilité de déterminer graphiquement la valeur exacte de l’ordre de multiplicité du point de tangence (m) et de reconnaitre graphiquement la relation de tangence grâce aux points convergents dont les représentants sont en position de superposition à l’écran (voir la fig-5 ci-dessous).
Selon les scénarios sus-évoqués, la configuration de la relation de tangence change. Autrement dit, on peut obtenir une droite tangente qui recoupe la courbe ou une droite tangente qui ne recoupe pas sa courbe associée, car, tous les points non attrapables auraient convergé vers le point de tangence A. Par suite, l’observation du comportement des points non attrapables peut être productive d’apprentissage sur la compréhension de la configuration finale de de relation de tangence.

 6.5 Justification théorique de la technique mise œuvre

Dans le cadre de la critique de cet article, le chercheur Gilles Aldon soulève la nécessite de préciser la théorie qui sous-tend notre technique. Car, pour lui, il est difficile de faire superposer le point sur la courbe et le futur point de tangence : « il n’y a pas superposition ou alors la droite n’existe plus. C’est bien tout l’enjeu du calcul infinitésimal ! ». Nous sommes bien en accord avec Gilles Aldon sur le fait que l’environnement GeoGebra procède à des approximations. Mais il nous semble que ces approximations favorisent l’enseignement de la notion d’ordre de multiplicité d’un point tangence (lorsque la courbe possède une valeur de (p) finie). Notre intérêt pour le logiciel réside aussi à ce niveau-là. Car lorsque les représentants des points A et B ont des coordonnées analytiques identiques dans la fenêtre algèbre, on peut alors faire coïncider les représentants des points A et B en utilisant les zooms inverses dans la fenêtre géométrique. Même avec un arrondi de 15 décimales, on peut toujours arriver à faire en sorte que les coordonnées analytiques des points A et B soient identiques dans la fenêtre algèbre. Car, il suffit de poursuivre avec le rapprochement du point sur la courbe vers le point fixe sur la courbe, jusqu’à ce que ces arrondis soient pris en compte par le logiciel. C’est-à-dire, jusqu’à ce que tous les coordonnées des points convergents deviennent identiques dans la fenêtre algèbre. Ceci, est rendu possible dans ce milieu, grâce à la coordination des fonctionnalités zoom et déplacement, qui permet de rapprocher sans cesse et autant que nécessaire, le point B sur la courbe vers le point fixe sur la courbe. A ce point de saturation l’on peut se servir des zooms inverses pour faire coïncider dans la fenêtre géométrique les représentants des points A et B. Ainsi, un point de vue de la droite tangente peut émerger dans la classe. Il s’agit de celui qui présente la droite tangente comme étant une droite qui forme avec la courbe à la position du point fixe une intersection dont l’ordre de multiplicité est supérieur ou égal à deux.

 7. Cadres théoriques de référence

 7.1 La théorie des champs conceptuels

À propos de la notion de tangence, nous avons, à partir des notions de racines simples, de racines multiples et de racines complexes d’une fonction numérique, défini les notions de points d’intersections simples, d’ordre de multiplicité du point de tangence, points non attrapables, points convergents et de points tombants. Nous avons également une technique géométrique et dynamique permettant de transformer dans l’environnement GeoGebra une relation de sécance en relation de tangence (lorsque la valeur de (p) est finie). Au cours de cette transformation un point non attrapable peut acquérir, entre autres, le statut de point convergent ou de point tombant. Nous cherchons à faire en sorte que le participant prenne appui sur ces scénarios possibles pour construire des connaissances prédicatives, lui permettant d’élaborer des conditions suffisantes (et non nécessaire dans un cas) visant à « justifier » pourquoi une droite tangente peut traverser sa courbe associée ou ne pas la recouper. Ainsi la notion de point de tangence constitue au moins en partie un objet d’apprentissage. Notamment, les raisons du changement de son ordre de multiplicité.
La théorie des champs conceptuels (Vergnaud, 2001) indique un moyen permettant de construire des sens sur des concepts mathématiques. Elle propose la conceptualisation dans l’action.
Poursuivant cette visée, nous allons donner au participant des occasions de construire à l’aide de la technique sus-décrite des relations de tangences, dont les configurations placent la droite tangente dans l’une ou l’autre des positions susmentionnées. Le choix de lui faire acquérir, en premier ressort, ces connaissances sous la forme opératoire, vise la conceptualisation sur les notions mathématiques en jeu, par l’adaptation des schèmes antérieurs (Vergnaud, 1999, 2001). Notamment, par le développement des composantes invariants opératoires, règles d’action, prise d’information et de contrôle et la composante inférence du schème de construction des relations de tangences de l’élève. La médiation de l’enseignant viendrait en cas de besoin guider l’élève davantage sur les connaissances opératoires.

Le concept de schème

L’auteur de la théorie des champs conceptuels présente le concept de schème sous des prismes différents. Pour (Vergnaud, 2001) le couple schème-situation est : « le couple théorique central de la psychologie du développement et de l’apprentissage, de la didactique et de la pédagogie. » (p.4). Le chercheur explique que, l’expérience et l’apprentissage sont adaptations, et précise que : « ce qui s’adapte ce sont des schèmes, et ils s’adaptent à des situations. » (p.4). Il propose alors quatre compréhensions du concept de schème. Dans le cadre de ce travail la définition 3 ci-dessous nous intéresse tout particulièrement :

1. Un schème est une totalité dynamique et fonctionnelle
2. Un schème est une organisation invariante de l’activité pour une classe définie de situations.
3. Un schème est nécessairement composé de quatre catégories de composantes
   –  Un but (ou plusieurs), des sous buts et des anticipations
   –  Des règles d’action, de prise d’information et de contrôle
   –  Des invariants opératoires (concepts-en-acte et théorèmes -en-acte). La conceptualisation prend appui sur les invariants opératoires. Le processus de conceptualisation du réel consiste à former à la fois des concepts-en-acte et des théorèmes-en-acte.

  7.2 La théorie des perspectives sur les fonctions

  7.2.1 Présentation des outils théoriques et méthodologiques à convoquer

Les perspectives sur les fonctions (Delgadillo et al., 2016 ; Alory et al., 2015 ; Vandebrouck, 2011) donnent des outils permettant d’analyser suivant trois angles les propriétés de certains objets mathématiques : « Par perspective, nous entendons des vues spécifiques dans le travail sur les fonctions, associées aux trois types de propriétés des fonctions : ponctuelles, locales et globales  » (Vandebrouck, 2011, p.8).

  7.2.2 Perspectives ponctuelles

Les perspectives sont différentes façons d’explorer une fonction, selon les propriétés mathématiques prises en considération (Panero, 2018). On peut étudier une propriété d’une fonction numérique $f$, valide qu’en un seul point. Autrement dit, la propriété dépend de la valeur prise par la fonction en ce point. Par exemple, $x= 3$ est un zéro de la fonction $f$, cet énoncé est une propriété ponctuelle, car elle ne donne pas d’information sur $f(x_0)$ pour tout $x_0 \neq 3$ Aussi, on peut s’intéresser à une propriété valide sur un ensemble fini de points. Par exemple, la courbe de la fonction $f$ coupe l’axe des abscisses aux points $A (0, 0)$, $B (1, 0)$ et $C (-2, 0)$. Cet énoncé est une propriété ponctuelle, car elle ne fournit pas d’information sur l’ordonnée $f(x_1)$, pour $x_1$ n’appartenant pas à l’ensemble fini $\{-2,0,1\}$. Elle dépend uniquement des valeurs prises par la fonction $f$ aux points d’abscisses $x_A$, $x_B$ et $x_C$ . Dans les cas sus évoqués, une perspective ponctuelle est activée sur la fonction.

  7.2.3 Perspectives globales sur les fonctions

Nous pouvons plutôt nous focaliser sur une propriété d’une fonction numérique $f$ valide sur un ou des intervalles. Par exemple, la fonction $f$ est croissante sur l’intervalle $[-1 ;1]$. Cet énoncé est une propriété globale, car elle est valable sur un intervalle (Vandebrouck, 2011). Elle permet d’activer une perspective globale sur la fonction f. Ainsi, une propriété globale permet de penser la fonction comme un tout (Panero, 2018), comme une unité (Rogalski, 2012) sur laquelle une caractéristique singulière se manifeste dans un intervalle. La périodicité, la croissance, la continuité, la dérivabilité globale sont quelques propriétés globales des fonctions numériques inscrites dans les curricula des classes de première et de terminale au lycée.

  7.2.4 Perspectives locales sur les fonctions

Nous pouvons aussi nous intéresser à une propriété d’une fonction numérique $f$, valide sur une famille de voisinages du point considéré. Par exemple, la courbe représentative de la fonction $f$ admet un minimum en $x_0=-2$ . Cet énoncé est une propriété locale, car elle dépend des valeurs prises par la fonction f sur un voisinage de aussi petit soit-il (Vandebrouck, 2011). Dans ce cas une perspective locale est activée sur la fonction, mettant en avant une propriété de la fonction $f$.

  7.2.5 La place de la théorie des perspectives sur les fonctions dans ce travail

Cette théorie soutient qu’une technique graphique mise en œuvre pour travailler sur la notion de fonction peut avoir un potentiel local plus élevé par rapport à une technique algébrique ou numérique (Panero, 2018 ; Vandebrouck, 2011). Nous choisissons alors de faire travailler le participant dans un environnement de géométrie dynamique, à l’aide de la technique sus-décrite, afin d’éprouver son potentiel local.
Par ailleurs, cette théorie soutient également que la mise en fonctionnement et en articulation des perspectives locale, ponctuelle et globale témoignent de la mise en place d’un processus de construction de la compréhension de la notion de fonction. Dans cette optique, elle nous permettra d’évaluer, d’apprécier ou de réguler la qualité des connaissances prédicatives construites sur la notion de relation de tangence par les participants, aussi bien dans l’environnement de géométrie dynamique que dans le cadre analytique.

 8. Technique de collecte de données

Nous avons conçu une situation d’enseignement de la notion d’ordre de multiplicité du point de tangence, et par suite, de la relation de tangence que nous avons menée auprès d’un public de lycéens au Cameroun. La technique de collecte de données que nous avons retenue est le Teaching Experiment (Dufour, 2019). Il s’agit d’une technique de collecte de données propre à la didactique des mathématiques. Elle a principalement été développée à l’école russe et plus récemment aux États-Unis par, entre autres, Steffe et Thompson (Steffe et al., 2000 ; Steffe & Thompson, 2000). Elle consiste en des séances d’enseignement orchestrées par un enseignant-chercheur qui a ainsi la possibilité d’interagir avec les apprenants et d’intervenir dans les interactions entre les apprenants en vue d’évaluer, d’orienter et de réguler les connaissances construites. Ceci a pour but de s’assurer que les apprenants surmontent la difficulté annoncée par la recherche et surtout de comprendre et d’expliquer comment ils y parviennent. Dans un Teaching Experiment, outre l’enseignant chercheur, il y a un chercheur-témoin et des participants. Le chercheur-témoin participe à l’élaboration des tâches à proposer aux participants et donne son avis sur l’interprétation des données, dans le but de renforcer l’objectivité du chercheur-enseignant. Dans notre Teaching Experiment, le rôle d’enseignant-chercheur a été tenu par l’auteur de l’article, celui de chercheur-témoin par un enseignant de lycée. Les participants sont quatre volontaires d’une classe de l’enseignant, choisis en collaboration entre le chercheur et l’enseignant. Ils avaient des genèses d’usage développées par rapport à la géométrie dynamique, ceci dans le but de faciliter l’instrumentalisation des fonctionnalités nécessaires à la construction dynamique de la droite tangente. Les outils de collecte de données étaient : une caméra à chaque poste, les cahiers des participants, un journal de bord pour des prises de notes avant, pendant et après les séances. Les instruments de collecte de données étaient : un guide d’observation utilisé pendant les séances et un guide d’entretien avec l’élève après les séances.

 9. Les situations d’enseignement proposées aux participants

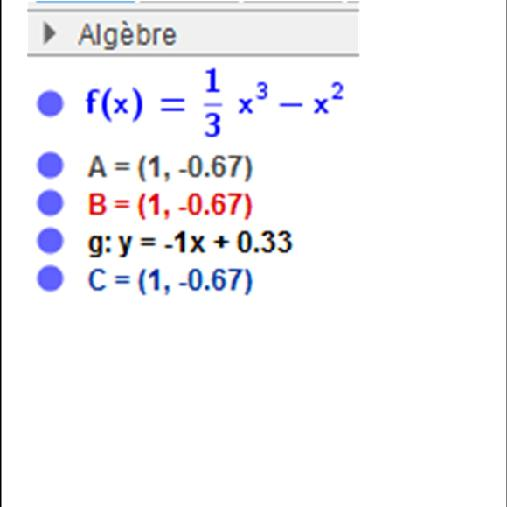
On considère la courbe (c) représentative de la fonction $f$ définie par $f(x)=\dfrac{x^{3}}{3}-x^{2}$, $A=\left(\begin{array}{c}1 \\ \frac{-2}{3}\end{array}\right)$ et $B$ un point sur (c). (m) désigne le nombre de point convergents et (p) le nombre maximal de points d’intersection simples que peuvent former la courbe et une droite sécante passant par le point $A$.

 9.1 Situation1 : Construction de sens sur la notion d’ordre de multiplicité du point de tangence

 9.2 Situation 2 : Une condition suffisante et non nécessaire pour qu’une droite tangente ne recoupe pas sa courbe associée

 9.3 Situation 3 : Définition de droite tangente en utilisant le concept d’ordre de multiplicité du point de tangence

 10. Le choix des productions à analyser

La séance, décrite et analysée en partie, s’inscrit dans une séquence d’enseignement visant à faire évoluer les conceptions actuelles de quatre lycéens sur la notion de tangence. Nous nous sommes rendus à la 11e séance sur les 13 séances prévues. Le participant X est celui qui a assisté à toutes les séances. Deux participants ont abandonné après la 5e séance. Le participant Y était présent lors de la 11e séance, mais était absent pendant 5 séances successives. Raisons pour lesquelles nous faisons le choix de présenter et d’analyser les productions du participant X. Suites à des phases de formulation et d’institutionnalisation au cours des dix premières séances, il a aussi acquis un nouveau langage ou vocabulaire consistant et ne figurant pas dans les manuels scolaires. Le but de cette séquence d’enseignement est de proposer au Ministère des Enseignements Secondaires (MINESEC) du Cameroun, une organisation praxéologique centrée sur l’utilisation de la géométrie dynamique et susceptible de faire de la droite tangente et du cercle tangent de véritables objets d’étude en classe de première ou de terminale.

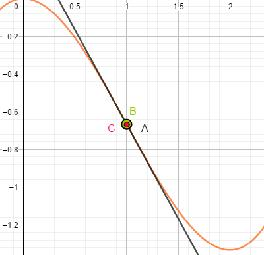
 11. Les productions du participant X relatives à la question (4)

 12. L’abscisse du point tangence en étude est une racine triple de la fonction

[p:x\longmapsto f(x)-T(x)]

Le participant X a utilisé la technique proposée pour construire la tangente à la courbe et a bien remarqué que les trois points se superposaient à l’écran. Il en déduit l’ordre de multiplicité de la racine de $p(x)$ en A.
En termes de perspectives sur les fonctions, la perspective de l’intersection d’une sécante à une courbe qui est à la fois globale (il y a trois points d’intersection sur le domaine étudié) et ponctuelle (A, B, C sont des points d’intersection de la sécante et de la courbe) permet, dans son expérience sensible sur GeoGebra, d’approcher une perspective locale de la tangente.
En termes de conceptualisation, l’expérience menée a permis au participant X de sélectionner les informations sur le nombre de points qui venaient se confondre à l’écran et de faire la relation avec l’ordre de multiplicité des racines, donnant ainsi une interprétation algébrique à la droite tangente à la courbe en A.
Cette expérience sensible sur le logiciel n’aurait pas été possible dans un environnement papier/crayon ce qui nous amène à soutenir que les fonctionnalités disponibles dans l’environnement GeoGebra rendent ce milieu propice pour donner un sens au concept d’ordre de multiplicité du point de tangence dans le cadre géométrique, sans faire un détour dans le cadre de l’analyse mathématique.
Ce bref extrait met en évidence les potentialités de cette approche pour peu que le lien entre l’expérience et les interprétations algébriques ou analytiques puissent être menées. Nous faisons l’hypothèse que, dans des conditions favorables, l’approche décrite permet de faire ce lien entre la construction géométrique de la tangente et sa définition analytique en favorisant une perspective locale de la tangente.

 13. Les productions du participant X relatives à la question (5)

 14. L’ordre de multiplicité d’un point de tangence A situé sur une courbe à valeur de (p) finie est égal à l’ordre de multiplicité de la racine $x_A$ de la fonction $p:x\longmapsto f(x)-T(x)$

Pour résoudre sa tâche le participant a mis au cœur de sa stratégie les points confondus à l’écran. Autrement dit, il s’est intéressé au point de tangence de la fonction en termes de points qui sont allés se superposer à l’écran à la position du point fixe, lors du passage de la sécante à sa position limite. Dans le cas de cette fonction, il a réussi a donner une interprétation analytique de la superposition des représentants des points convergents. Mettant ainsi, en relation l’ordre de multiplicité du point de tangente A (compris géométriquement) avec l’ordre de multiplicité de l’abscisse du point de tangence $x_A$, lorsqu’elle est racine de la fonction $p:x\longmapsto f(x)-T(x)$. Par la suite la composante inférence du schème du participant lui a sans doute permis de transformer la conjecture faite à partir du cas de la fonction en étude, en une connaissance prédicative, mise en italique dans le cadre ci-dessus. Il nous semble alors que, regarder l’ordre de multiplicité du point de tangence en termes de points convergents pourrait être une approche intéressante en classe ordinaire, permettant au lycéen de donner un autre sens à ce concept dans le cadre de l’analyse mathématique, pour les courbes à valeurs de (p) finies.

 15. Les productions du participant X relatives à la tâche (6)

 15.1 Les productions graphiques du participant X relatives à la tâche (6)

 15.2 Les productions écrites du participant X relatives à la tâche (6)

 16. Ordre de multiplicité du point de tangence : un outil permettant de produire une équation algébrique de la droite tangente à la courbe d’une fonction à valeur de (p) finie

Pour résoudre sa tâche, le participant X a articulé le cadre géométrique et le cadre de l’analyse mathématique. La construction du point de tangence lui permis de déterminer le nombre de points convergents. Ainsi, il a utilisé le sens donné à ce concept dans l’environnement de géométrie dynamique pour déterminer graphiquement sa valeur. Puis il l’a articulé avec le sens analytique, pour la production d’une équation algébrique de la droite tangente. Les productions graphiques du participant X montrent que la droite tangente traverse sa courbe au point d’inflexion. Nous avançons l’hypothèse que la configuration graphique de la relation de tangence n’a pas été une entorse à la reconnaissance de la droite tangente, sans doute parce qu’il a pensé la relation de tangence en termes de nombre de points convergents en position de superposition à l’écran. Il nous semble alors que, dans l’environnement de géométrie dynamique, les points convergents en position de superposition, pourraient être des outils intéressants en classe ordinaire, permettant à un lycéen, de reconnaitre graphiquement une relation de tangence dans différentes configurations évoquées dans la problématique.
Il nous semble également que, ce type de tâche pourrait être une piste intéressante en classe ordinaire, permettant au lycéen de penser géométriquement la relation de tangence, avant de procéder à une interprétation dans le cadre de l’analyse mathématique. Contrairement au point de vue proposé par la dérivation qui présente la pente comme étant un objet premier par rapport à la droite tangente, cette approche propose de faire de la droite tangente un objet premier par rapport à sa pente.

 17. Les productions écrites du participant X relatives à la tâche (7)

 18. L’ordre de multiplicité du point de tangence est toujours supérieur ou égal à deux

L’argumentation du participant X ci-dessus encadrée montre qu’il a convoqué la notion de point fixe, de point sur la courbe et de point non attrapable pour résoudre sa tâche. Au cours de la résolution de la tâche 2, la composante concept-en-acte du schème du participant lui a permis de sélectionner les informations sur les comportements des points sus-évoqués, comme des informations essentielles pour appréhender le concept d’ordre de multiplicité du point de tangence. Et la composante inférence du schème du participant lui a permis de relier ces informations et d’en prendre appui pour construire sa justification. Ainsi, regarder l’ordre de multiplicité du point de tangence comme étant le nombre de points convergents, lui a permis de se construire un modèle géométrique et dynamique de compréhension de ce concept, qui repose, entre autres, sur les éventuels comportements des points non attrapables et sur le comportement du point sur la courbe. Ce modèle de compréhension lui a permis de construire une argumentation satisfaisante du point de vue de la géométrie dynamique, lui permettant d’expliquer pourquoi l’ordre de multiplicité du point de tangence est toujours supérieur ou égal à 2. Il nous semble alors que, la visualisation de la convergence du point sur la courbe et éventuellement des points non attrapables, jusqu’à superposition à l’écran de leurs représentants, pourrait être une approche intéressante en classe ordinaire, pour faire en sorte qu’un lycéen, comprenne et explique suivant le point de vue de la géométrie dynamique, pourquoi l’ordre de multiplicité du point de tangence est toujours supérieur ou égal à deux.

 19. Les productions du participant X relatives à la tâche (8)

 20. La relation (p) = (m) : une condition suffisante pour qu’une droite tangente ne recoupe pas sa courbe associée, dans le cas de courbe de fonction à valeur de (p) finie

Pour proposer sa condition suffisante (et non nécessaire), le participant X s’est inspiré du modèle de construction du point de tangence A, mis en œuvre dans l’environnement de géométrie dynamique. Au vu de son argumentation, nous avançons l’hypothèse qu’au cours de la résolution de la tâche (2), la composante concept-en-acte du schème du participant lui a permis de sélectionner les informations sur la valeur (p) et sur la valeur (m) comme des informations importantes pour appliquer le principe de la conservation du nombre de points, entre le nombre de points (p) d’intersection de la relation de sécante stricte (point sur la courbe, points non attrapables) et le nombre de points convergents (m). La composante prise d’informations du schème du participant lui a permis de constater que, dans le cas de la relation de tangence en étude, on a (m)= 3 = (p) et que la droite tangente ne recoupe pas sa courbe associée. Par suite la composante inférence du schème du participant lui a permis d’appliquer le principe de la conservation pour transformer cette dernière information en une connaissance prédicative mise en italique dans le cadre ci-dessus.
Il nous semble alors que, le modèle de construction de la relation de tangence pourrait être un modèle intéressant en classe ordinaire, pour qu’un lycéen arrive à justifier suivant le point de vue de la géométrie dynamique, pourquoi la droite tangente ne recoupe pas sa courbe associée.
Par ailleurs, la valeur de (m) est égale au nombre de points convergents. Sa détermination a sans doute activé chez le participant des perspectives locales sur la fonction au voisinage du point de tangence. La mise en fonctionnement de ces perspectives locales pour proposer la condition suffisante suscitée, laisse croire qu’il y a eu évolution de la conception algébrique chez le participant X. Car, cette conception n’intègre pas les perspectives locales sur la fonction pour penser la notion de droite tangente. Dès lors, il nous semble que le nombre de points convergents pourrait être un outil intéressant en cours ordinaire, pour provoquer le développement des perspectives locales sur la fonction au voisinage du point de tangence dans le cas des courbes à valeur de (p) finie.

 21. Les productions du participant X relatives à la tâche (9)

 22. La relation (p)= 2 =(m) : une raison de la géométrie dynamique pour laquelle le cercle ne recoupe pas sa droite tangence

Le participant X centre son argumentation ci-dessus encadrée, sur le principe de la conservation du nombre de points, entre le nombre de points (p) d’intersection de la relation de sécance stricte et le nombre de points convergents (m), pour expliquer pourquoi la droite tangente ne recoupe pas le cercle. Il s’est intéressé au nombre de points convergents. En particulier, à l’unique point sur le cercle dont le représentant est allé se superposer à la position du futur point de tangence. Ce qui nous laisse croire que la visualisation du mouvement des points convergents jusqu’en position de superposition à l’écran, pourrait être un instrument intéressant en classe ordinaire, pour la mise en fonctionnement et l’articulation des perspectives globale, ponctuelle et locale sur la notion de cercle au voisinage du point tangence. Afin d’appliquer le principe de la conservation susmentionnée.
Adopter une vision locale sur le cercle au voisinage du point de tangence peut laisser penser qu’il a eu évolution de la conception Unique Point d’Intersection chez le participant X. Car, cette conception n’intègre pas les perspectives locales sur le cercle pour penser la notion de droite tangente. Ce qui nous laisse penser, que le nombre de points convergents pourrait être un outil intéressant en classe ordinaire, pour le développement des perspectives locales sur le cercle au voisinage du point de tangence.

 23. Les productions du participant X relatives à la tâche (10)

 24. Une condition suffisante pour qu’une droite tangente traverse sa courbe associée, dans le cas des courbes de fonctions polynômes

Pour résoudre sa tâche le participant X a pris appui sur le sens qu’il a donné au point d’inflexion dans l’environnement de géométrie dynamique. Au vu des connaissances prédicatives et opératoires ci-dessus encadrées, nous avançons alors l’hypothèse qu’au cours de la construction du point de tangence, la composante concept-en-acte du participant lui a permis de sélectionner les informations sur les comportements des points convergents, comme des informations essentielles pour appréhender le concept de point d’inflexion. Par la suite, la composante inférence du schème du participant lui a permis de relier ces informations et de les transformer en un modèle de compréhension mis en italique dans le cadre ci-dessus. Ce modèle géométrique de compréhension du point d’inflexion lui a permis de montrer que, si (m) =3 alors la fonction $x\longmapsto f(x)-T(x)$, change de signe en l’abscisse du point de tangence. Ce qui nous laisse croire que, le mouvement des points convergents induit par la technique mise en œuvre pour construire un représentant du point d’inflexion, pourrait être une piste intéressante en classe ordinaire, pour la construction de la condition suffisante sus-évoquée. Par ailleurs, cette condition est centrée sur le nombre de points convergents et sur les sens des déplacements des points non attrapables vers la position du futur point de tangence. Il nous semble alors que la technique mise en œuvre pour construire un représentant du point d’inflexion pourrait être une approche intéressante en classe ordinaire, pour la mise en fonctionnement et l’articulation des perspectives locales sur la fonction, afin de convoquer les sens de déplacements des points non attrapables, comme essentiels à la compréhension de la notion de point d’inflexion. Une interprétation judicieuse du sens inverse des déplacements desdits points aurait probablement permis au participant d’étendre à d’autres courbes la condition suffisante susmentionnée.
Ainsi, il nous semble que, la possibilité de mettre en relation tous les points d’intersection simples d’une relation de sécance stricte, et d’en transformer certains en des points convergents, pourrait être une approche intéressante en classe ordinaire, pour la reconnaissance graphique de la droite tangente lorsqu’elle traverse sa courbe associée. Dès lors que le lycéen se focaliserait sur la visualisation des représentants des points convergents en position de superposition à l’écran.

 25. Les productions du participant X relatives à la tâche (11)

 26. Définition d’une droite tangente à partir du sens donné à l’ordre de multiplicité du point de tangence dans l’environnement GeoGebra

Les connaissances prédicatives du participant X ci-dessus encadrées montrent que celui-ci a réussi à donner une définition plus générale de la notion de droite tangente, en prenant appui sur le sens qu’il a donné au concept d’ordre de multiplicité du point de tangence, dans l’environnement de géométrie dynamique. L’enseignant a souhaité que dans l’action, l’apprenant construise des sens sur ce concept, afin de le conduire à rédiger la définition de la droite tangente liée à ce même concept. Cet itinéraire cognitif prévu par l’enseignant a porté de bons fruits auprès de l’apprenant. Car les connaissances prédicatives ci-dessus encadrées montrent que le participant a pris appui sur le nombre de points convergents pour justifier sa proposition de définition. Il s’est inspiré de la technique mise en œuvre pour construire le point de tangence afin de soutenir que le nombre de points convergents est toujours supérieur ou égal à deux. Nous avançons alors l’hypothèse qu’en situation, la composante concept-en-acte du participant lui a permis de considérer ces informations comme essentielles pour la généralisation de la définition d’une droite tangente. Par la suite la composante inférence du schème du participant lui a permis de transformer ces informations en une connaissance prédicative mise en italique dans le cadre ci-dessus. Au vu, de son argumentation, il nous semble que, la visualisation du comportement des points convergents (points non attrapables), pourrait être une approche intéressante en classe ordinaire, pour faire en sorte que le lycéen arrive, à proposer et s’approprier une définition générale de la droite tangente, fondée sur le concept d’ordre de multiplicité du point de tangence.

 27. Les productions du participant X relatives à la tâche (12)

 28. Production d’une équation algébrique de la droite à partir du sens construit sur le concept d’ordre de multiplicité du point de tangence

Le participant X est arrivé à produire une équation algébrique de la droite tangente à la courbe de la fonction : $x\longmapsto\sin(x)$ au point d’abscisse $\frac{\pi}{4}$, en prenant appui sur les sens construits sur le concept d’ordre de multiplicité du point de tangence. Le premier sens présente l’ordre de multiplicité du point de tangence comme étant le nombre de points confondus à la position du point fixe A. Le second sens a consisté à considérer que l’ordre de multiplicité du point de tangence A est égal à $n$, si et seulement si, le réel $x_A$ est une racine d’ordre $n$ de la fonction $x\longmapsto f(x)-T(x)$. Ces deux sens donnés ont permis au participant X d’élargir à d’autres courbes, les connaissances opératoires et prédicatives construites sur la notion de droite tangente, dans le contexte des courbes à valeur de (p) finie. Car, le participant a compris en situation qu’il n’est pas absolument nécessaire de connaitre la valeur exacte de l’ordre de multiplicité du point de tangence, afin de déterminer une équation algébrique de la droite. Il nous semble que, la notion de nombre de points convergents, pourrait être un outil intéressant en classe ordinaire, pour faire en sorte que le lycéen élargisse à d’autres courbes la définition de la droite construite dans le contexte des courbes à valeur de (p) finie.
Par ailleurs, les connaissances opératoires et prédicatives du participant X ci-dessus encadrées, montrent que celui-ci a mis en articulation et en fonctionnement les perspectives locale, globale et ponctuelle, lors de la convocation de l’ordre de multiplicité du point de tangence, afin de produire une équation algébrique de la droite tangente. Ce qui nous amène à soutenir que, la notion de nombre de points convergents, pourrait être un outil intéressant en cours en ordinaire, pour faire en sorte que le lycéen pense la notion de droite tangente à la courbe d’une fonction suivant des perspectives locales.

 Conclusion

Nous avons considéré des constatations empiriques. Des élèves capables de démonter algébriquement qu’une droite tangente recoupe sa coupe ou ne la coupe pas. Cependant, même après démonstrations, des élèves posent, entre autres, la question suivante : pourquoi une droite tangente recoupe-elle sa courbe associée dans certains cas et pas dans d’autres ? Nous avons également considérer des constations théoriques. Certains lycéens ayant une pensée gouvernée par la conception Unique Point d’Intersection, ont des difficultés à reconnaitre graphiquement la droite tangente lorsqu’elle traverse sa courbe associée ou lorsqu’elle ne la recoupe pas (Dufour, 2019 ; Delgadillo et al., 2016).
Pour chercher des éléments de réponses aux difficultés sus-évoquées, nous avons construit des situations d’enseignement ayant pris la forme d’un Teaching Expériment, dont l’enseignant est l’auteur de cet article. Ces situations d’enseignement ont pris appui sur l’environnement GeoGebra. Notamment, en y rendant opérationnel une technique de construction du point de tangence. Elle est une adaptation d’une technique rendue opérationnelle dans le même environnement par (Nguembou-Nana, 2022). Nous avons alors présenté les insuffisances de cette première technique, en lien avec la construction d’une compréhension géométrique et dynamique de la notion d’ordre multiplicité du point tangence.
Nous avons alors fat en sorte que les participants acquièrent des connaissances opératoires permettant de construire un point de tangence en lequel la droite tangente traverse sa courbe associée sans la recouper. Visant ainsi, la conceptualisation dans l’action de la notion de point tangence et en particulier de l’ordre de multiplicité du point de tangence.

Une première définition de l’ordre de multiplicité du point de tangence est proposée par l’enseignant à la classe. Elle voudrait que la valeur de (m) soit égale au nombre de points convergents. C’est-à-dire, au nombre de points confondus liant la courbe et sa tangente. Grâce à cette définition, le participant X a réussi a donner un nouveau sens à ce concept, valide dans le cadre de l’analyse mathématique. Pour lui, l’ordre de multiplicité du point de tangence devient alors égal à l’ordre de multiplicité de la racine $x_A$ de la fonction $x\longmapsto f(x)-T(x)$. Cette nouvelle relation a permis au participant X de produire une équation algébrique de la droite tangente à la courbe d’une cubique en son point d’inflexion suivant une vision locale. En ayant préalablement déterminé dans l’environnement GeoGebra, la valeur de (m).
Le travail susmentionné du participant X, nous a invité à soutenir que l’environnement de géométrie dynamique, par la possibilité qu’elle offre de visualiser le mouvement des points convergents vers le futur point de tangence, jusqu’à superposition de leurs représentants, pourrait devenir en classe ordinaire une piste, pour présenter ou pour faire appréhender l’ordre de multiplicité du point de tangence comme étant le nombre de points convergents. De même, la possibilité de visualiser des points convergents en position de superposition à l’écran, et de l’interpréter en termes de points confondus liant la courbe et la droite tangente, pourrait devenir, en classe ordinaire, une piste pour établir que l’ordre de multiplicité du point de tangence est égal à l’ordre de multiplicité de l’abscisse du point de tangence en tant que racine de la fonction Ce sont là deux concepts importants, l’un est lié au cadre géométrique pendant que l’autre est lié au cadre de l’analyse mathématique.
Par ailleurs ce modèle géométrique et dynamique de compréhension du concept d’ordre de multiplicité du point de tangence, pourrait en classe ordinaire être une piste pour développer chez le lycéen les perspectives locales sur des courbes à valeurs de (p) finies. Mais également, pour être une piste intéressante, lui permettant de reconnaître les relations de tangence, aussi bien dans le cadre du cercle que dans le cas des fonctions à valeurs de (p) finies. Dès lors que ce dernier se focaliserait sur les points convergents en position de superposition à l’écran.

 Limite de l’étude

Au cours de cette étude, pour des raisons susmentionnées, nous avons réduit notre échantillon au seul participant X. Qui vraisemblablement possède une capacité d’abstraction et de généralisation élevée. Ces motifs affaiblissent toute velléités de généralisation des résultats obtenus au cours de cette recherche. Au demeurant, ces résultats sont des pistes exploitables pour aider le lycéen à surmonter les difficultés relatives à l’apprentissage de la notion de droite tangente et évoquées dans la section problématique. Une étude portant sur un échantillon plus large permettrait sans doute de confirmer ou d’infirmer plus aisément les hypothèses avancées dans ce travail.

 Bibliographie

Alory, S., Chorlay, R., Derouet, C., Josse, V., Legris, C., Loeng, R., Panero, M., Rogalski, M., & Vivier, L. (2015). Autour de la notion de dérivée en classe de première. IREM de Paris, N° 97.101.
Artigue, M. (1989). Épistémologie et didactique. (Numéro 3). IREM de Paris. https://hal.archives-ouvertes.fr/hal-02138030
Balacheff, N. (1995). Conception, connaissance et concept. Séminaire de l’équipe DidaTech, IMAG, Grenoble, France. pp.219-244 24.
Balhan, K., Krysinska, M., & Schneider-Gilot, M. (2015). Quelle définition du concept de tangente  ? Pour quelles raisons  ? Repères : Revue des Instituts de Recherche sur l’Enseignement des Mathématiques, 101 (Octobre 2015).
Delgadillo, E. M., Murillo, R. P., & Vivier, L. (2016). Conceptions spontanées et perspectives de la notion de tangente pour des étudiants de début d’université. First conference of International Network for Didactic Research in University Mathematics, , Montpellier, France.
Dufour, S. (2019). Des processus de compréhension sous l’angle des représentations  : Un Teaching Experiment autour de la dérivée. 298. Thèse de doctorat, Université du Québec à Montréal.
Duval, R. (1994). Sémiosis, pensée humaine et activité mathématique. Amazônia : Revista de Educação em Ciências e Matemáticas, 6(1), 126‑143.
Gantois, J.-Y. (2012). Un milieu graphico-cinématique pour l’apprentissage des dérivées dans une praxéologie « modélisation »  : Potentialités et limites. Thèse de doctorat, Université Liège. 392.
Maschietto, M. (2002). La transition algèbre / analyse au lycée dans l’environnement des calculatrices graphiques et formelles  : quelques éléments. Thèse de doctorat en co-tutelle, Université de Paris 7 - Denis Diderot, Dell’Università Degli Studi Di Torino.
Maschietto, M. (2003). Le rôle de la calculatrice dans le développement du langage autour du jeu global / local. (Discours) présenté à la conférence CIEAEM 53 - Alphabétisation mathématique dans le numérique a eu lieu à Verbania du 21 au 27 juillet 2001.
Maschietto, M. (2004). Le jeu entre point de vue local et point de vue global en Analyse  : Une ingénierie didactique à visée diagnostique au niveau première. Actes du colloque de Mulhouse 8-9 mars 2020, IREM de Strabourg.
Nguembou-Nana. (2022). La géométrie dynamique, un instrument pour la construction de sens sur le concept de position limite : Une étude de cas auprès des lycéens de classe de première scientifique au Cameroun. Revue MathémaTICE, n°82, Novembre 2022.
Panero, M. (2018). Les pratiques enseignantes concernant la dérivée dans le secondaire. séminaire national de didactique des mathématiques 2016, Paris, France.304‑324. https://ardm.eu/manifestations/seminaire-ddm-ardm/
Restrepo, A. (2008). Genèse instrumentale du déplacement en géométrie dynamique chez des élèves de 6eme. Thèse de doctorat, Université de Joseph- Fourier
Rogalski, M. (2012). Approches épistémologique et didactique de l’activité de formalisation en mathématiques. Actes du colloque EMF2012. 10.
Rouy, E. (2007). Formation initiale des professeurs (du secondaire supérieur) et changement de posture vis-à-vis de la rationalité mathématique. Thèse soutenue à l’université de Liège
Steffe, L., Thompson, P., & Glasersfeld, E. (2000). Teaching experiment methodology  : Underling principles and essential elements. Handbook of research design in mathematics and science education, 267‑306.
Tall, D. (1985). Chords, tangents and the Leibniz notation, Mathematics teaching, 112, 48-52.
Vandebrouck, F. (2011). Des technologies pour l’enseignement et l’apprentissage des fonctions du lycée à l’université  : Activités des élèves et pratiques des enseignants. Université Denis Diderot - Paris 7. 137.
Vergnaud, G. (1999). À quoi sert la didactique  ? Revue sciences humaines - Hors-série n° 24 - mars/avril 1999.
Vergnaud, G. (2001). Forme opératoire et forme prédicative de la connaissance. Conférence publiée dans les Actes du Colloque GDM-2001. 22.
Vivier, L. (2010). Un milieu théorique pour la notion de tangente dans l’enseignement secondaire. IREM de strasbourg, 15, 28.