En début de CM2, les évaluations diagnostiques montrent que l’algorithme de la multiplication posée n’est généralement pas compris, même de ceux qui savent appliquer la procédure. Parmi les prérequis, la compréhension de la numération décimale et la connaissance des tables de multiplication, font le plus souvent défaut. Quelques éléments de remédiation sont proposés. La procédure étant bien connue des enfants, même si elle est insuffisamment comprise, il est proposé de l’aborder d’une manière différente et encore inédite pour eux, en leur présentant sous forme d’énigmes, la multiplication par jalousie et les bâtons de Napier.

Introduction

Dans la brochure éduscol sur le calcul aux cycles 2 et 3, à la rubrique « calcul posé », on lit :

Le calcul posé permet de disposer d’une méthode de calcul sécurisante, car elle permet de garantir l’obtention d’un résultat. Le calcul posé permet l’étude du fonctionnement d’algorithmes complexes à partir de leur mise en pratique.

Vaste programme ! À l’élève que j’étais à l’école, je ne me souviens pas qu’on ait expliqué à quoi correspondaient toutes les procédures qu’on faisait répéter de manière automatisée pour calculer une multiplication, ou bien alors ne l’ai-je pas compris. Du moins, je n’en ai pas le moindre souvenir. Certes, ça ne m’a pas empêchée d’apprendre à faire des multiplications. Ça ne m’a même pas empêchée de devenir professeur des écoles, ni même d’enseigner les maths. En revanche, lorsque je fus confrontée aux difficultés de mes élèves, il a fallu que je remette en question ce que je croyais savoir faire de manière évidente sans jamais avoir pris la peine, depuis les bancs de l’école, de me demander ce que je faisais vraiment. Il a fallu que je m’interroge sur ces difficultés, sur les obstacles rencontrés, sur ce qu’il y avait là à comprendre en réalité pour réussir. Réussir, c’est-à-dire, réussir vraiment, de manière experte ; en comprenant chacune des actions qui constituent l’algorithme de calcul et de manière à ne plus oublier les étapes de l’opération ou bien encore, les astuces de la maîtresse pour compenser les incompréhensions.

Cet article relate mes interrogations et propose quelques pistes, en décrivant la séquence effectivement mise en place cette année dans ma classe de CM2. Les opérations posées étant au programme, je ne me pose pas la question de leur utilité, donc je ne rentrerai pas dans le débat sur l’opportunité d’enseigner des algorithmes arithmétiques, à l’heure des calculettes et des ordinateurs. Pour un point relativement récent sur la question, voir Fisher et al. (2019). Comme on le verra, je crois utile de ne pas me limiter à un seul algorithme, et j’ai expérimenté une approche historique, utilisant la multiplication par jalousie et les bâtons de Napier : voir A. Busser et N. Daval (2016). La didactique de la multiplication par jalousie est développée par R. Chorlay, F. Mailloux et B. Masselin (2017). L’efficacité de la méthode a été évaluée par A. Rebakawati (2017). Une autre approche historique possible est celle de la multiplication égyptienne, discutée entre autres par M.-J. Madrid et al. (2021).

Deux documents pdf sont proposés en accompagnement. Le premier contient le stock d’exemples historiques dans lequel étaient puisées les énigmes matinales, le second donne les références et le contexte des œuvres dont elles sont issues.

Le constat

D’une part, il y a de quoi remettre en question nos méthodes d’enseignement : il s’agit en effet pour l’enseignant de maîtriser lui-même les ressorts des différentes étapes de l’opération et ce qu’il s’agit de faire comprendre aux enfants. D’autre part, les prérequis nécessaires à cet apprentissage ne sont pas toujours en place, notamment la bonne compréhension de la numération et du système décimal, qui en début d’année ne semble pas acquise pour tous non plus. Les erreurs faites par les enfants sont souvent interprétables par l’une ou l’autre de ces défaillances.

De plus, une autre question a rapidement émergé : pourquoi est-ce si important de comprendre comment fonctionne l’algorithme de l’opération, quand moi, j’ai bien réussi à le reproduire suffisamment pour en faire une compétence acquise et quand de nombreux élèves y parviennent tout autant ? Mettre du sens sur l’algorithme permet-il de mieux dominer la technique opératoire ? Pourtant censée être aquise en fin de cycle 2, je constate en CM2 que la maîtrise de l’opération n’est pas satisfaisante pour beaucoup d’élèves. Même parmi ceux qui me semblent parvenir à reproduire la technique enseignée, certains se trouvent en difficulté si je les oblige à verbaliser les procédures de résolution de l’opération : soit parce qu’ils ne comprennent pas le sens de ce qu’ils font, soit parce qu’ils n’ont pas le vocabulaire technique nécessaire à la description des calculs — et le plus souvent les deux. Le moindre obstacle au déroulement de l’algorithme est alors source d’erreur.

Ce qui suit est basé sur les résultats d’un exercice d’évaluation diagnostique, dans lequel il était demandé de justifier toutes les étapes d’une multiplication, en répondant à la question : « à quel calcul correspond ce résultat ? ».

Les propriétés de la multiplication : distributivité, associativité, commutativité

Dans leur article Des mathématiques à leur enseignement — l’algorithme de la multiplication, Clivaz et Deruaz soulignent l’importance des « quatre connaissances mathématiques spécifiques que sont la distributivité, l’associativité, la numération décimale de position et finalement la définition de la multiplication, sous-jacente à ces propriétés. » Ils précisent « que ces connaissances ne sont pas toutes maîtrisées par de futurs enseignants en formation », et soulignent « les difficultés d’enseignement générées par une maîtrise insuffisante de ces connaissances par les enseignants ». Autant dire que ces manques ne sont pas toujours compensés par les formations —insuffisantes— en mathématiques et qu’elles se retrouvent dans les classes, au moment de transmettre ce qu’on n’a peut-être pas soi-même assez profondément compris.

Le lien n’est pas toujours suffisamment fait entre l’algorithme de la technique opératoire et le calcul réfléchi afin de faire émerger des procédures individuelles une procédure unique : l’algorithme dont on attend des élèves qu’ils puissent le reproduire. L’utilisation implicite et automatisée des propriétés de la multiplication ne permet pas aux élèves de les identifier ni de les comprendre. Il s’agirait plutôt de pouvoir les faire remarquer, verbaliser et manipuler avant d’automatiser leur utilisation dans l’opération « posée ». Encore ne suffit-il pas de décrire les opérations mentales nécessaires aux différentes étapes, mais aussi de les expliquer et d’en faire expérimenter les ressorts.

Voici ce que donne la compréhension « experte » de l’opération — rarement verbalisée par les élèves, et à laquelle il faudrait pouvoir parvenir :

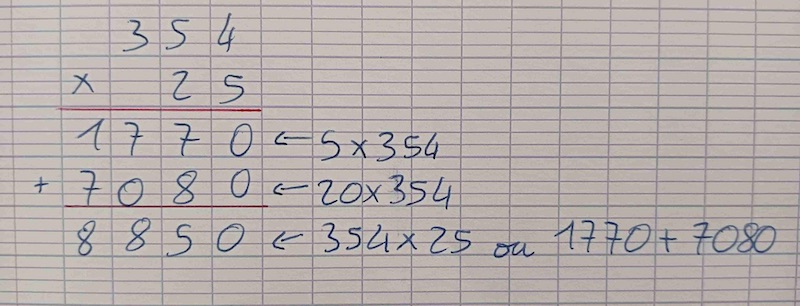
Le sens du zéro dans les « étages »

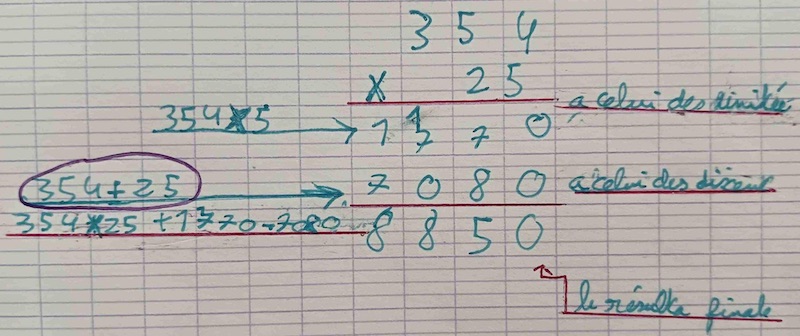
Lorsque les élèves multiplient un nombre par un nombre à deux chiffres, ils ont appris à « ajouter un zéro » avant de procéder aux calculs de la deuxième ligne. Certains même l’écrivent en rouge pour ne pas l’oublier : ils utilisent un moyen mnémotechnique et s’en sortent ainsi. D’autres procèdent directement aux calculs par le chiffre des dizaines, sans considérer que ce sont des dizaines. Car là est bien le problème : en réalité, les enfants ne savent pas ce qu’ils multiplient dans l’opération, ni pourquoi ils le font. Ils manipulent des alignements de chiffres les uns après les autres, sans comprendre qu’ils manipulent des nombres.

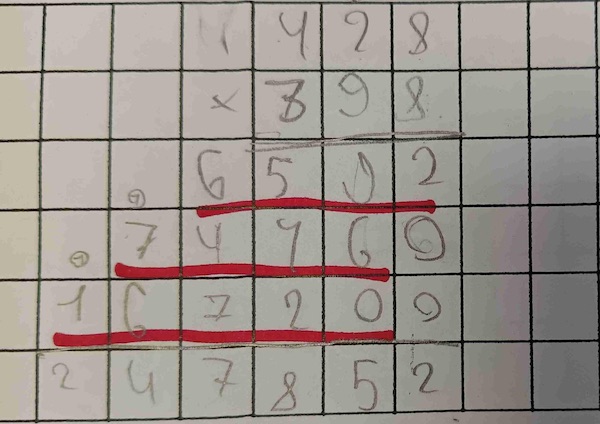
Les retenues et la compréhension de la numération

Si la numération n’est pas en place, les élèves se heurtent au problème des retenues : quand la retenue n’a pas de sens, on ne sait guère quoi en faire : l’additionner, la multiplier ? Les élèves les plus en difficulté sont parfois très créatifs pour arriver à « faire quelque chose » de tous ces chiffres qu’on leur présente, et produire un résultat, quel qu’il soit, puisque c’est ce qu’on leur demande. La technique opératoire devient une succession d’actions dont l’élève ne saisit ni le sens ni l’objectif : la mécanique est creuse.

Les tables

Un autre problème peut faire obstacle aux élèves : les tables de multiplication. Depuis le CE2, les élèves sont censés les connaître par cœur. Je ne doute pas d’ailleurs que cet apprentissage soit fait : je fais réviser les élèves de CE2, puis de CM1, lorsqu’ils font leurs devoirs à l’étude. Ce sont les mêmes élèves que je retrouve en CM2… et qui ne les connaissent toujours pas. Ce travail de mémorisation doit d’abord s’appuyer sur la compréhension du fonctionnement des tables de multiplication. On peut ensuite les faire mémoriser comme une poésie, en les répétant par cœur, ce qui arrive le plus souvent, comme je l’ai moi-même fait à l’école, où nous ânonnions tous en cœur chaque matin. Mais cela ne suffit pas : pour être mobilisables rapidement et que cet apprentissage ait du sens, il faut aussi les leur faire construire, les faire apprendre à l’envers, dans le désordre et en relation avec la division.

Une proposition de séquence d’apprentissage en CM2

Au début du CM2, lors des évaluations diagnostiques menées à la rentrée, on constate que le sens de l’opération n’est pas toujours compris par un grand nombre d’élèves. Les tables de multiplication ne sont pas vraiment sues. La technique opératoire est approximative, et les erreurs des enfants révèlent souvent une incompréhension, ne serait-ce que du sens de l’opération et de différentes étapes du calcul posé, sans même rentrer dans les détails de ce qui s’y passe.

Le travail sur la multiplication à ce stade de la scolarité est censé n’être qu’un travail de consolidation des connaissances et des techniques déjà acquises lors des classes précédentes, il apparaît comme tel dans les programmes, mais pour un certain nombre d’élèves, les savoir-faire et les applications des techniques apprises ne sont que des répétitions mécaniques et la compréhension réelle des procédés n’en est que très fragile.

Néanmoins, la multiplication étant un élément bien connu des enfants, compris ou pas, il est judicieux de l’aborder d’une manière différente et encore inédite pour eux afin de susciter leur intérêt et leur curiosité pour consolider des procédures qu’ils pensent déjà savoir maîtriser.

Multiplication par jalousie

Je l’aborde sous la forme d’une situation-problème en proposant aux élèves une énigme.

Les enfants sont habitués à ce format d’énigme historique, qui est présenté depuis le début de l’année en numération. Ils ont pour consigne, cette fois, de découvrir ce qui est représenté sur l’image, et d’expliquer comment ça fonctionne. Il s’agit d’un travail de recherche en groupes, durant lequel les enfants peuvent échanger. Il doivent produire une réponse commune et argumentée sur le sens qu’ils donnent à ce qu’ils observent. A priori, les enfants n’ont jamais vu cette méthode de calcul, toutefois, des indices sur l’image peuvent les orienter sans peine : les mots écrits en latin, « multiplicandus » et « numerus multiplicans » qui évoquent évidemment la multiplication, et « summa », qui doit leur rappeler le terme de « somme » qu’ils ont déjà croisé.

D’ailleurs, ils comprennent très vite qu’il s’agit de multiplication, certains évoquent une table de Pythagore —qu’ils ont déjà vue— certains identifient que le résultat de chaque case est le produit d’une multiplication. Ils tentent différents calculs mais aucun élève ne parvient spontanément au cours de la séance à identifier qu’il s’agit d’une opération ni à comprendre d’où provient le nombre en bas du tableau.

Il faudra attirer leur attention sur le mot « summa » et redéfinir le mot « somme » pour qu’ils finissent par comprendre. Pour vérifier leur hypothèse - il s’agit d’une multiplication, les enfants sont invités à poser l’opération comme ils ont appris à le faire. La plupart des élèves finissent par trouver le même résultat.

Cette énigme est la première d’une série du même genre :

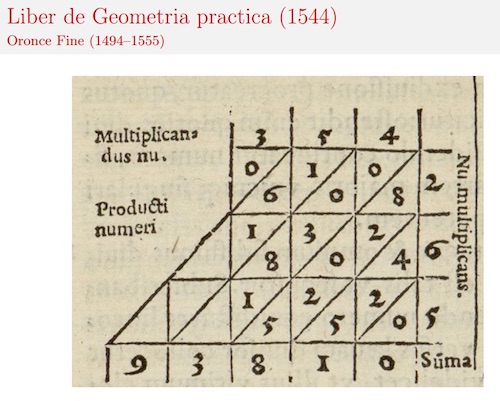Les premières sont données telles quelles, les enfants ayant pour consigne de comprendre comment était fait le calcul, et de le vérifier en posant à leur tour l’opération selon la méthode traditionnelle, jusqu’à trouver le même résultat.

Comme l’élève de cette vidéo les enfants parviennent rapidement à refaire le calcul selon la technique de jalousie. Il n’en est pas toujours de même au moment de la vérification.

Cet exercice a révélé des difficultés importantes dans la maîtrise de la technique opératoire, pourtant censée être bien connue des élèves. Les tables de multiplication n’étaient pas bien sues, l’opération en elle-même, au fil des étages, était parfois parsemée d’erreurs de calculs ou de retenues. L’erreur la plus inquiétante quant à la bonne compréhension du procédé concernait les « zéros » à ajouter à chaque étage de l’opération, le plus souvent oubliés, ou mal comptés. Les calculs étant corrigés collectivement, et expliqués oralement par les enfants, il s’est avéré que la plupart d’entre eux n’étaient pas capables d’expliquer les différentes étapes de calcul, quand bien même elles étaient justes.

La situation suivante a posé problème : les enfants ont remarqué que le tableau n’était pas orienté de la même manière que les fois précédentes, et se sont heurtés à la vérification, le calcul ayant été lu comme « 7435×723 » alors qu’il s’agissait de « 7435×327 ».

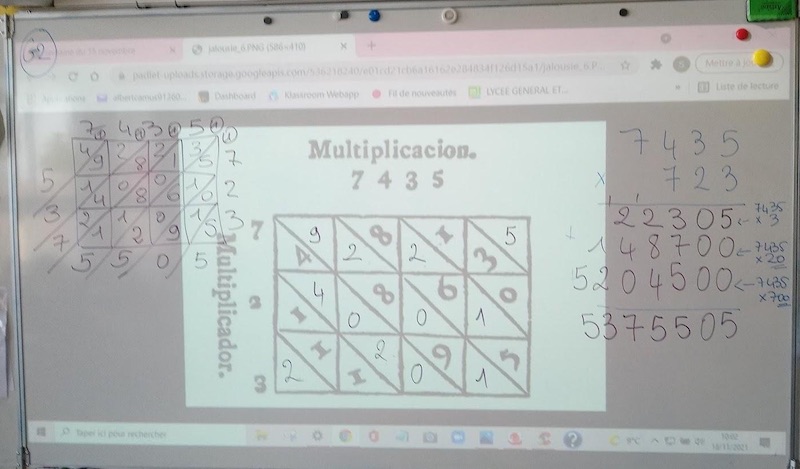
Néanmoins, on peut voir sur la photo la routine de résolution adoptée pour notre désormais rituel du matin : les jalousies sont peu à peu éclaircies de leurs résultats, pour les faire compléter par les enfants, et la méthode traditionnelle vient valider le premier résultat obtenu.

Chaque étape de la technique opératoire est détaillée, comme par exemple ici :
7435×723 = (7435×3) + (7435×20) + (7425×700) suivant le caractère de distributivité, en expliquant que 723, c’est 700+20+3 soit sept centaines, deux dizaines et trois unités.

Ce sont en réalité les propriétés de la multiplication qui n’ont pas été comprises des enfants et probablement pas assez manipulées, notamment en calcul mental ou dans les calculs en ligne.

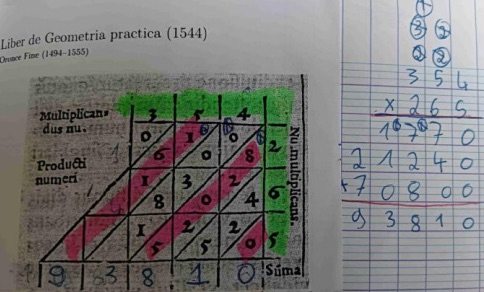
Bâtons de Napier

Un jeu avec les bâtons de Napier a ensuite été proposé aux élèves. La manipulation des bâtons à plusieurs atouts : l’objet éveille leur curiosité, la manipulation permet de lire les étapes intermédiaires de l’opération sans avoir à mobiliser les tables de multiplication. Même les élèves des plus petites classes que j’ai eus à l’étude ont voulu observer le matériel et le manipuler, puis se sont essayés à la méthode par jalousie.

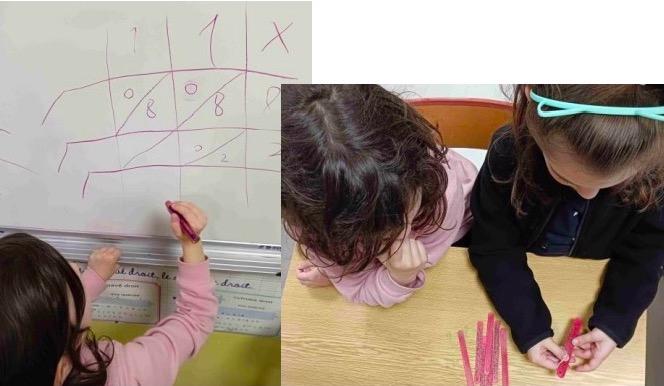
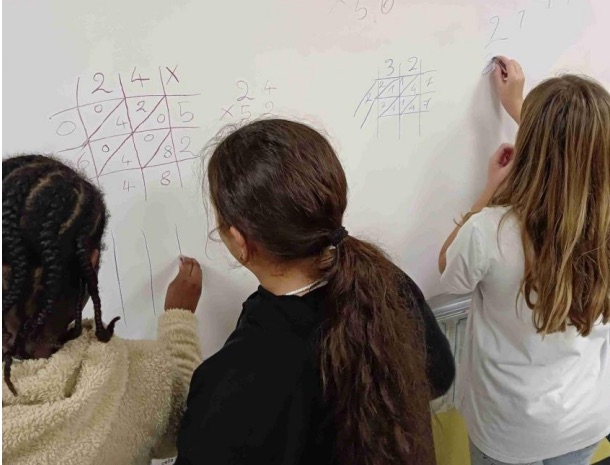
Exercices d’évaluation

Afin de fluidifier les procédures, des exercices rituels de calculs sont proposés aux enfants. Ces exercices sont chronométrés pour inciter les enfants à choisir les stratégies de calcul les plus efficaces.

Sont travaillées aussi bien les additions (chercher les compléments à dix en priorité) que les multiplications.

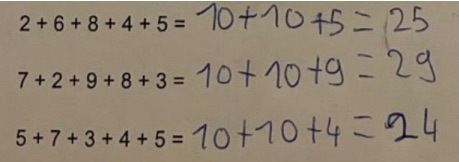
Les tables de multiplication

En parallèle, afin de consolider l’apprentissage des tables de multiplication, les enfants ont redécouvert la table de Pythagore imagée.

Les points ont permis de visualiser le sens de l’opération. Les enfants ont été invités à compléter la table de Pythagore avec les nombres correspondants. Des tables de multiplications « simplifiées » ont également été données, afin de montrer que 4×6, c’est aussi 6×4 : savoir l’un, c’est savoir l’autre. Des jeux de révisions ont été mis en place afin d’automatiser les apprentissages ; de permettre aux enfants de s’évaluer et de continuer à s’entraîner. Des générateurs de tests sont disponibles sur le site de Charivari.

Les escaliers de l’école aussi ont été mobilisés pour l’occasion, car il n’y a pas de petite occasion d’apprendre et qu’investir les lieux, c’est aussi se saisir de ses apprentissages : le groupe d’élèves bénéficiant des Activités Pédagogiques Complémentaires sur le temps du midi a été chargé de cette mission de la plus haute importance et top secrète, pour garder l’effet de surprise aux autres élèves de l’école. Effet réussi, qui a suscité jusqu’à la curiosité et l’enthousiasme des plus petits de l’école.

Ce fut un travail pratique qui a permis de réinvestir d’autres compétences et l’occasion aussi de travailler les mesures pour réfléchir à une disposition équilibrée des panneaux sur les marches.

Conclusion

Pour répondre aux questionnements qui ont initié cette séquence : expliciter le sens de l’algorithme permet-il de constituer une aide dans l’efficacité des calculs, notamment pour les élèves qui rencontrent des difficultés dans son apprentissage et son exécution ? Sans aucun doute, c’est indispensable : le passage par la technique de la jalousie permet aux élèves dans un premier temps de se sentir en confiance et en réussite. Tous les élèves parviennent à trouver le résultat. La résolution parallèle de l’opération avec la technique traditionnelle permet aux enfants d’être autonomes dans la validation de leur résultat — l’intérêt étant de chercher, analyser et comprendre son erreur quand les deux résultats ne coïncident pas. Ils sont acteurs de leur apprentissage et de leur progression. La verbalisation systématique des procédures — si elle n’est pas toujours suffisante, invite les élèves à réfléchir aux nombres qu’ils manipulent et aux opérations mentales qu’ils doivent mener. Ils sont d’ailleurs souvent étonnés de comprendre soudainement ce qu’il leur semblait déjà savoir faire.

À la question : cela permet-il d’améliorer d’autres compétences mathématiques, au-delà de la maîtrise de la technique opératoire ? La compréhension de l’algorithme oblige à revenir sur l’aspect positionnel de la numération et sur la décomposition des nombres, la technique opératoire oblige à la manipulation des nombres, ce qui en effet, constitue « l’occasion de travailler les principes de la numération » comme le stipulent les programmes.