En appelant régiment le couple d’adultes ci-dessus, on retrouve le cas particulier n=2 du régiment de n soldats à faire passer sur l’autre rive avec un bac ne permettant de faire passer qu’un adulte ou deux enfants à la fois. On peut résoudre ce problème récursivement, avec cette solution pour n=1 d’abord :

• Les deux enfants traversent seuls.
• L’un des deux enfants revient seul.
• L’adulte traverse.
• Le second enfant revient.

Cette solution est emblématique de la programmation dynamique parce que le fait d’avoir résolu le problème dans un cas particulier simple, aide à le résoudre dans le cas général :

(état actuel : n+1 adultes et les deux enfants avec le bac sur la rive gauche)

• Les deux enfants traversent seuls.
• L’un des deux enfants revient seul.
• Un adulte traverse.
• Le second enfant revient.

(on est alors à l’état : n adultes avec les deux enfants et le bac sur la rive gauche). L’algorithme est donc récursif.

En représentant la rive gauche par l’équation x=0 et la rive droite par l’équation x=1, chaque état possible est un point de l’espace de dimension 4 (dans l’ordre, les abscisses du loup, de la chèvre, de la pomme et du bateau). Les coordonnées de ces points valant 0 ou 1, ces points sont les sommets d’un tesseract. Mais le graphe n’est pas celui du tesseract. Par exemple, dans un tesseract, il y a une arête entre les sommets (0,0,0,0) et (1,0,0,0). Dans le cas présent cette arête représenterait la traversée de la rivière par le loup sans utiliser le bateau. Pour avoir des arêtes du tesseract, il faut échanger la quatrième coordonnée d’un sommet sur deux, comme le montrent les couleurs ci-dessous (source : wikipedia) :

Sur les sommets blancs, la 4e coordonnée représente l’abscisse t du bateau, sur les sommets colorés, la 4e coordonnée représente 1-t. Il peut maintenant y avoir une arête reliant les points (0,0,0,0) et (1,0,0,1) car ces points ne sont pas de la même couleur (les coordonnées de l’état (1,0,0,1) étant représentées par le point (1,0,0,0) puisque ce point est colorié).

Parmi les 16 sommets du tesseract, certains sont impossibles, ils correspondent aux états suivants :

• (0,0,0,1) (le batelier a laissé le loup, la chèvre et la pomme sans surveillance)
• (1,1,1,0) (idem mais en inversant les rives occupées)
• (0,0,1,1) (le loup et la chèvre sont seuls sur la rive gauche).
• (1,1,0,0) (idem mais sur la rive droite)
• (1,0,0,1) (la chèvre et la pomme sont seules sur la rive gauche)
• (0,1,1,0) (idem, sur la rive droite).

En enlevant ces 6 sommets (et les arêtes adjacentes à ceux-ci) on obtient un graphe simplifié à 10 sommets. Résoudre le problème revient alors à parcourir ce graphe, ce qui est facile une fois le graphe tracé (il a la forme d’une molécule de para-diéthylbenzène).

Une solution sera modélisée par une liste d’entiers, selon la représentation suivante :

• L’entier 0 représente la traversée du loup (accompagné automatiquement du batelier).
• L’entier 1 représente la traversée de la chèvre (accompagnée automatiquement par le batelier).
• L’entier 2 représente la traversée du chou (et du batelier).
• L’entier 3 représente la traversée du batelier seul.

Voici une fonction qui transforme ces entiers en leurs hiéroglyphes (ou plutôt, une liste d’entiers, en une chaîne de caractères) :

Comment construire toutes les listes d’entiers égaux à 0, 1, 2 ou 3 ? En fait ces entiers sont des chiffres en base 4. On peut donc construire une liste d’entiers à partir d’un entier, en écrivant celui-ci en base 4 puis en convertissant chaque chiffre (un caractère) en entier. Pour cela on a besoin d’une fonction Python de conversion en base 4. En voici une récursive [1] :

Pour implémenter les arêtes du graphe (ou les changements d’état de l’automate), on va créer une fonction qui, à un état state et un personnage quidam, associe

• soit le même état state si le quidam ne peut pas traverser depuis l’état state,
• soit le nouvel état s (obtenu à partir de l’état state après que quidam a traversé).

Pour ce faire on crée un futur état en copiant state, puis on effectue le changement d’état sur ce nouvel état (pour garder l’ancien état au cas où le changement d’état ne serait pas possible). Pour effectuer le changement d’état,

• Si quidam n’est pas le bateau, on le fait traverser en modifiant la coordonnée de numéro quidam de l’état.
• Dans tous les cas, le batelier traverse aussi.

Ensuite,

• si quidam n’est pas le bateau et que le bateau et quidam ne sont pas du même côté de la rivière, c’est que le quidam a traversé à la nage. On signale alors une erreur de type (traverser sans le bateau c’est un peu comme essayer d’additionner un nombre avec du texte) ;
• si le loup et la chèvre sont sur une même rive et que le bateau n’est pas du même côté, on signale là aussi une erreur de type (les types loup et chèvre étant en quelque sorte incompatibles) ;
• si la chèvre et la pomme sont du même côté qui n’est pas celui du bateau, là encore une erreur de type (incompatibilité entre la chèvre et la pomme) ;
• Si tout le monde est à droite on signale non pas une erreur mais une exception StopIteration disant que le problème est résolu.
• Dans tous les autres cas on renvoie le nouvel état puisque la traversée a réussi.

Cette fonction se code ainsi en Python :

Pour résoudre le problème du loup, de la chèvre et de la pomme, on peut alors faire ainsi :

• on boucle sur les numéros numtrajet des trajets possibles dans le graphe (par ordre croissant) ;
• pour chacun de ces numéros, on le convertit en liste d’entiers (transitions possibles) à partir de son écriture en base 4 ;
• on initialise l’état à [0,0,0,0] ;
• pour chaque transition, on essaye de changer l’état jusqu’à la survenue d’une exception ;
• en cas de StopIteration on affiche la suite des transitions (convertie en mot) parce que celle-ci est une solution au problème.

En allant jusqu’à 10000 on obtient ce script :

qui affiche ces deux solutions :

• 🐐 🚣 🐺 🐐 🍏 🚣 🐐
• 🐐 🚣 🍏 🐐 🐺 🚣 🐐

Le logiciel libre Cubicle, développé par Alain Mebsout et Sylvain Conchon, fait de la vérification de modèles : il cherche si un état dangereux (« unsafe ») peut être atteint lors de l’évolution d’un système. Il peut donc servir à résoudre le problème du loup, de la chèvre et de la pomme, en considérant que l’état souhaité (tout le monde sur la rive droite) est dangereux. On utilise des variables booléennes, précisant si le loup est à droite, si la chèvre est à droite, si la pomme est à droite et si le bateau est à droite. Une autre variable booléenne V sert à forcer au moment adéquat la transition no_problemo qui ne fait que vérifier qu’il n’y a pas de problème (et n’est donc pas une vraie transition puisque personne ne traverse).

L’état initial est décrit par ces variables toutes égales à False (personne n’est sur la rive droite puisque tout le monde est sur la rive gauche) :

init() { Loup_droite=False && Chevre_droite=False && Pomme_droite=False && Bateau_droite=False }

L’état final (« unsafe » donc) est le contraire : tout le monde est sur la rive droite :

unsafe() { Loup_droite=True && Chevre_droite=True && Pomme_droite=True && Bateau_droite=True }

Cubicle va essayer de voir si l’état final unsafe peut être atteint à partir de l’état initial. Pour cela, il faut préciser les transitions permettant de passer d’un état à un autre. Il y a déjà les 4 traversées des protagonistes. Par exemple le loup traverse s’il est du même côté que le bateau (prérequis à la traversée : le loup ne sait pas nager) et si la traversée est autorisée (V), et la traversée a pour effet de modifier les propositions « le loup est sur la rive droite » et « le bateau est sur la rive droite » :

Une fois la traversée effectuée, V est positionnée à False pour empêcher tout autre changement d’état avant de vérifier que tout est OK. Les traversées de la chèvre et de la pomme sont similaires, et celle du bateau est plus simple puisqu’il traverse alors seul :

Pour vérifier que tout va bien, on ajoute une fausse transition no_problemo qui n’est activée que si V est niée (donc après chaque vraie traversée) et dont le prérequis est constitué de deux implications :

• Si le loup est du même côté que la chèvre alors le bateau doit aussi être de ce côté.
• Si la pomme est du même côté que la chèvre alors le bateau doit aussi être de ce côté.

Une fois la vérification faite, la variable V est simplement repositionnée à True afin de permettre de tester d’autres traversées :

Voici l’intégralité du programme Cubicle :

En enregistrant ce fichier sous le nom loup.cub, on résout le problème avec la commande

./cubicle -dot 2  loup.cub

ce qui donne, d’une part l’affichage dans la console, de ce corrigé :

et d’autre part, le dessin de la solution comme parcours de cet arbre :

Résoudre ce problème, c’est trouver un chemin dans un graphe. Cela peut se faire notamment par un algorithme de parcours en profondeur, qu’Édouard Lucas a attribué à « Monsieur Trémeaux, ancien élève de l’École Polytechnique, ingénieur des télégraphes », dans ses récréations mathématiques, au chapitre sur les labyrinthes. En effet, sortir d’un labyrinthe, c’est aussi trouver un chemin dans un graphe.

Sébastien Hoarau a lui aussi opté pour un parcours du graphe en profondeur. Comme le parcours en profondeur utilise une structure de type LIFO (ou pile (informatique), au programme de NSI en Terminale), la solution de Sébastien Hoarau peut être exposée tôt dans l’année scolaire, les progressions choisies plaçant en général les piles vers le début de l’année scolaire.

Voici la solution de Sébastien Hoarau :

Chaque état est représenté par une liste de nombres égaux à 0 ou à 1 (autrement, un nombre entre 0 et 15, écrit en binaire). La méthode __init__ met ces 4 nombres à 0 puisqu’au début tout le monde est sur la rive gauche. La méthode d’affichage représente cette liste, en séparant les rives par une série de « tildes » représentant les vagues de la rivière. La méthode fini vérifie si l’état final est atteint.

Les méthodes memorise, oublie et deja_vu gèrent la pile (modèle de mémoire de travail du passeur) :

• memorise place l’état suivant au sommet de la pile, et effectue la transition en faisant en sorte que l’état suivant devienne l’état actuel ;
• oublie fait un peu l’inverse : l’état du sommet de la pile est éjecté d’icelle (oublié) et l’état précédent devient l’état actuel ;
• deja_vu vérifie si l’état en cours d’examen est déjà dans la pile (autrement, mémorisé et pas oublié)

La méthode danger vérifie si le loup peut manger la chèvre ou si la chèvre peut manger le chou (absence du passeur pour empêcher le massacre), sous forme d’expressions booléennes, et renvoie la disjonction de ces conditions ; la méthode traverse effectue le changement d’état, en modifiant les abscisses de ceux qui ont effectué la traversée, et la méthode resoud construit une solution récursivement, par l’algorithme de Trémeaux.

On constate que toutes ces fonctions sont définies comme des méthodes d’un objet seb appartenant à la classe Passeur : c’est le passeur qui mémorise les états explorés et qui résout le problème (en plus de ramer, accompagné par un loup, une chèvre ou un chou). L’exécution du script donne cet affichage :

• 🐺🐐🥬🙂 _________
• 🐺🥬_________ 🐐🙂
• 🐺🥬🙂 _________ 🐐
• 🥬 _________ 🐺🐐🙂
• 🐐🥬🙂 _________ 🐺
• 🐐 _________ 🐺🥬🙂
• 🐐🙂 _________ 🐺🥬
• _________ 🐺🐐🥬🙂

Unicode étant très pratiqué en Asie, le teint de Sébastien vire un peu au jaune (que l’on se rassure sur son état de santé, il sature bien en oxygène) et le chou est dessiné comme un pe-tsaï, très fréquent d’usage à La Réunion. Du moins lorsque le navigateur accepte de dessiner ce caractère...

Comme on le voit, et bien qu’il y ait plus de protagonistes que dans le problème du loup, de la chèvre et du chou, un état est un point de l’espace de dimension 3. La solution correspond donc à un parcours dans ce graphe en 3D :

Comme les arcs de ce graphe sont des vecteurs, le problème est géométrique et consiste en un système d’addition de vecteurs avec états [3]. Plus précisément, comme pour le loup, la chèvre et le chou, on va tenir compte de la parité du nombre de mouvements, et

• additionner un vecteur de la forme (l,d,1) à l’état courant si le bateau va de la rive gauche (état (x,y,0) puisque le bateau est à gauche) vers la rive droite (ce qui amène l licornes de plus et d dragons de plus à droite) ;
• soustraire un vecteur de la forme (l,d,1) à l’état courant si le bateau revient vers la rive gauche (ce qui enlève l licornes et d dragons de la rive droite pour les ramener à gauche, ainsi d’ailleurs que le bateau).

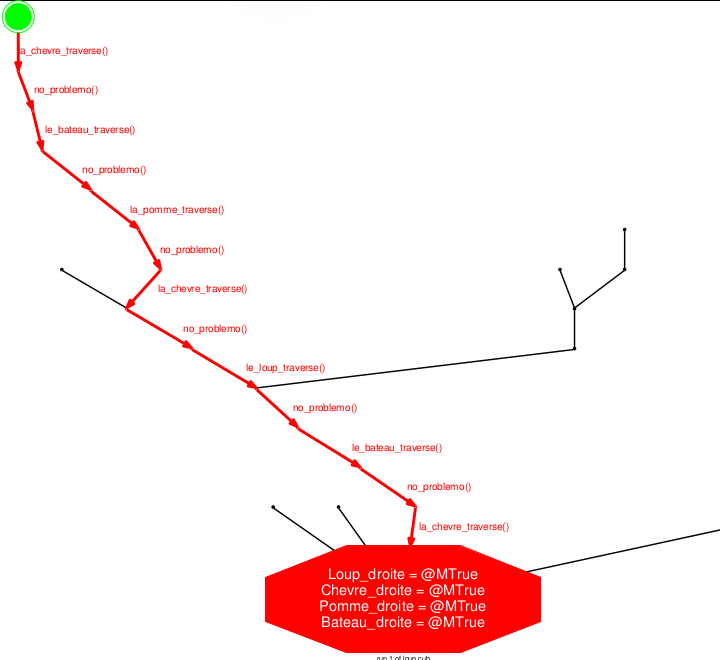
Voici une recherche exhaustive en Python s’inspirant de celle du problème « loup, chèvre, chou » vue auparavant :

L’affichage d’une transition représente la barque (deux flèches indiquant le sens de déplacement de celle-ci) et son équipage. Une transition est la donnée du nombre l de licornes qui traversent, du nombre d de dragons qui traversent, et du sens s de traversée :

Une variable globale donne, pour chaque chiffre en base 5 du trajet essayé, le nombre de licornes et le nombre de dragons qui traversent :

On remarque que cette partie du problème a été résolue sans passer par Python : ces 5 couples sont les seuls respectant les contraintes

• au moins un personnage dans le bateau (il ne traverse pas tout seul)
• pas plus de 2 personnages à la fois dans le bateau (capacité C du bateau limitée à 2)
• pas plus de dragons que de licornes dans le bateau

Il aurait été possible, en exercice préliminaire, de créer un script Python retrouvant les 5 couples d’entiers ci-dessus.

Comme il y a 5 transitions possibles, on a besoin d’une fonction de conversion en base 5 :

Le prochain état next dépend de l’état actuel state et de la transition radeau faisant passer d’un état à l’autre. En notant l, d et s les valeurs actuelles des variables de même nom (nombre de licornes sur la rive gauche, nombre de dragons sur la rive gauche et sens de déplacement du radeau), les valeurs après la traversée sont notées l2, d2 et s2. Comme la barque ne fait que des allers-retours, s2 est égal à 1-s. L’expression 1-2s vaut 1 ou -1 et a pour effet de déterminer si c’est une addition ou une soustraction qu’il faut effectuer (une traversée vers la droite fait diminuer le nombre de licornes ou de dragons sur la rive gauche, une traversée vers la gauche ramène du monde).

• La ligne 6 rappelle qu’à tout instant, les nombres de licornes et de dragons sur les deux rives doivent être positifs ou nuls.
• La ligne 8 rappelle que le seul moyen qu’il y ait plus de dragons que de licornes sur la rive gauche, est qu’il n’y ait pas du tout de licornes sur la rive gauche.
• La ligne 10 rappelle que le seul moyen qu’il y ait plus dragons que de licornes sur la rive droite, est qu’il n’y ait pas du tout de licornes sur la rive droite.
• Si ne serait-ce qu’une seule de ces conditions n’est pas respectée, la traversée est considérée comme impossible et l’ancien état est renvoyé par la fonction. La ligne 12 est celle qui n’est exécutée que si la transition est possible : elle renvoie le nouvel état (en réalité un triplet, Python rajoute les parenthèses sans qu’on ait à le lui dire) :

Pour chercher une solution à ce problème, il faut donc

• parcourir en largeur d’abord, l’arbre des possibilités, avec la conversion en base 5 ;
• pour chaque trajet possible, fabriquer les transitions sous forme d’une liste de triplets (l,d,s)
• initialiser l’état à 3 licornes, 3 dragons et une barque sur la rive gauche
• pour chacune des transitions, tenter de calculer le nouvel état (effectuer la transition)
• si à la fin, il n’y a plus ni licornes ni dragons sur la rive gauche, l’état final est atteint et on affiche la solution qui est la suite des transitions :

C’est très long : il faut des dizaines de millions d’itérations avant d’arriver à ces solutions :

• [’→🐉🐉→’, ’←🐉←’, ’→🐉🐉→’, ’←🐉←’, ’→🦄🦄→’, ’←🦄🐉←’, ’→🦄🦄→’, ’←🐉←’, ’→🐉🐉→’, ’←🦄←’, ’→🦄🐉→’]
• [’→🐉🐉→’, ’←🐉←’, ’→🐉🐉→’, ’←🐉←’, ’→🦄🦄→’, ’←🦄🐉←’, ’→🦄🦄→’, ’←🐉←’, ’→🐉🐉→’, ’←🐉←’, ’→🐉🐉→’]

En fait, il y a une autre solution qui aurait dû apparaître avant, mais son premier chiffre est 0 et elle n’a donc pas été calculée.

Dans les années 1950, au sein de RAND Corporation, Richard Bellman a développé une manière efficace pour gérer la récursivité dans des problèmes d’optimisation : la programmation dynamique. En 1962, il a publié des exemples d’utilisation de la programmation dynamique, parmi lesquels figure cette solution du présent problème :

Bellman applique la programmation dynamique à ce problème parce que la programmation dynamique sert à résoudre des problèmes d’optimisation sous contrainte, et que Bellman a réussi à interpréter ce problème comme un problème d’optimisation sous contraintes :

• la quantité à optimiser est le nombre total de protagonistes sur la rive droite (le maximum étant 6)
• les contraintes font que seuls ces 10 états sont possibles (en abscisse, le nombre de licornes sur la rive gauche, en ordonnée, le nombre de dragons sur la rive gauche) :

Par exemple le point de coordonnées (2,1) est grisé parce qu’il correspond à 2 licornes et un seul dragon sur la rive gauche, ce qui a priori ne pose pas problème, mais comme le nombre total de dragons et de licornes reste constant, cet état laisserait 1 licorne avec 2 dragons sur la rive droite et nous allons jeter un voile pudique sur ce qui se passerait alors...

Bellman propose alors de généraliser le problème, en ne regardant pas seulement l’état initial (3,3) mais aussi les états intermédiaires, et il calcule (récursivement, par programmation dynamique) le nombre total de licornes et de dragons pour chacun de ces états, au bout de N transitions.

Pour simplifier les calculs, Bellman considère comme transition, un aller-retour du bateau, de la rive gauche à la rive gauche, en amenant du monde à droite puis en en ramenant à gauche. Avec une exception : depuis l’état final on autorise exceptionnellement le bateau à revenir à vide, juste pour que cette transition aussi se termine avec le bateau à gauche.

Par exemple comme dans l’état final (0,0) on a 6 protagonistes (3 licornes et 3 dragons) sur la rive droite, on a f₀(0,0)=6 :

De façon similaire on peut calculer les valeurs de f₁ en certains points, en se basant sur celle déjà calculée :

Des valeurs de f₂ peuvent ensuite être calculées à partir des précédentes, ce qui entame une récursion :

Par exemple le fait que f₂(3,3)=2 signifie que depuis l’état initial (3,3) on peut, au mieux, en deux allers-retours, avoir 2 personnages sur la rive droite.

Une des caractéristiques de la programmation dynamique est que l’on résout des problèmes partiels et qu’ensuite on se sert de ces solutions pour résoudre le problème global, récursivement. Ce que fait Bellman pour estimer, pour chacun des états du graphe, l’indice N pour lequel f_N(état)=6. Il obtient alors ceci :

Comme chaque sous-problème intervient dans la résolution du problème global, les étapes de cette solution apparaissent en rouge : le fait que pour l’état initial (3,3) la valeur de N est 6 signifie d’une part que pour résoudre le problème à partir de (3,3) il faut 6 allers-retours du bateau (avec un retour à vide après le 6e aller), d’autre part que pour y arriver il faut passer par l’état pour lequel N=5. De part en part, la solution apparaît sur le graphe en regardant les valeurs décroissantes de N :

Une autre caractéristique de la programmation dynamique est qu’une fois qu’on connaît l’optimum, on peut s’en servir pour retrouver la manière de l’obtenir. Par exemple pour le début de la solution on doit, par un aller-retour du bateau, aller de (3,3) à (3,2) comme on le voit sur le graphe ci-dessus : une licorne fait un aller-retour (valeur 3 inchangée) et un dragon fait un aller simple. Cela ne peut se faire que par un aller dragon+licorne suivi par un retour de la licorne seule (en fait il y a une autre façon de faire, la voyez-vous ?).

Pour en savoir plus, voir ce document éduscol. La programmation dynamique est un des chapitres de NSI en terminale.

Cette très élégante solution est de Jean-Christophe Filliâtre, qui, entre beaucoup d’autres choses, est un des auteurs du manuel de NSI 24 leçons avec exercices corrigés - Terminale (édité chez Ellipses, ISBN : 9782340038554). L’idée est de dessiner le graphe et d’y chercher un chemin allant de l’état initial vers l’état final. Le graphe ne comporte que 20 sommets et environ le quart d’entre eux sont isolés. La tâche n’est donc pas si énorme qu’on le croirait au début.

Mieux encore, au lieu de dessiner le graphe à la main, on pourrait demander à Python de le construire (et même de le dessiner comme on verra plus bas). Il s’agit alors de traduire en Python les contraintes du problème et une fois le graphe construit (sous la forme d’un dictionnaire Python), de demander à Python de chercher le chemin à l’aide d’un algorithme de parcours en largeur. Jean-Christophe Filliâtre n’est pas l’auteur de cette méthode, qu’Édouard Lucas attribue [4] à un « Monsieur Maurice, ancien élève de l’École Polytechnique ».

Mais Jean-Christophe Filliâtre est l’auteur d’un livre (cité ci-dessus) où figurent justement des explications sur la manière de construire un graphe, et de le parcourir en largeur, en Python. Alors il suffit d’utiliser les ressources de ce livre pour avoir en une fraction de seconde la solution du problème, dessin à l’appui. Voici comment on peut utiliser sa solution ci-dessous :

• renommer graphe.py le fichier que voici ;
• renommer largeur.py le fichier que voilà ;
• compléter ce dernier fichier, en y ajoutant la fonction chemin qui calcule un chemin entre deux sommets du graphe (en cas de difficulté à faire cet exercice, il reste la possibilité d’acheter le livre et de copier le corrigé de cet exercice à la fin du livre) ;
• exécuter le script Python que voici :

L’exécution du script mène à cette solution :

en 11 déplacements du bateau (ce qui correspond bien aux 6 aller-retours du bateau vus par Bellman, puisque le dernier retour se faisait à vide).

Le module graphviz de Python permet également de dessiner le graphe ainsi construit, et voici le résultat :

Jean-Christophe Filliâtre n’est pas le seul auteur du manuel de NSI 24 leçons avec exercices corrigés - Terminale : un autre auteur de ce livre, Sylvain Conchon, est également (entre autres) développeur de Cubicle.

Cubicle, déjà décrit dans la partie sur le loup, la chèvre et la pomme, est un model checker qui permet de coder des systèmes de transitions et de vérifier si des états du système sont atteignables. Sylvain Conchon fait la remarque que

• les problèmes de traversée de rivière sont des systèmes de transitions (ici une traversée du bateau d’une rive à l’autre est une transition),
• la question posée par Alcuin est de savoir si un état peut être atteint (unsafe correspond à la situation où tout le monde est de l’autre côté, sain et sauf).

Cubicle est développé entre autres pour Intel, avec pour but de vérifier des protocoles de cohérence de cache dans les processeurs à plusieurs cœurs, et l’état dont on veut savoir q’il peut être atteint, est en fait celui qu’on veut éviter. L’idée est de prouver qu’un système est sûr par une exploration exhaustive d’un arbre pour prouver qu’il n’existe pas de contre-exemple. Par conséquent, le nom unsafe est donné à l’état cherché, alors que justement les licornes sont en sécurité dans cet état ! De même l’état initial (à partir duquel on voudrait savoir si unsafe peut être atteint) est appelé init.

Chaque transition est introduite par un prérequis (une proposition exprimant ce qui permet la transition) et ses effets sont décrits dans un langage de programmation propre à Cubicle et dont les affectations sont notées par le «  := » du langage Algol :

Noter que la règle des licornes (celle qui autorise la transition sans qu’une licorne ne soit dévorée) est rédigée sous forme d’implications :

• V doit être nié pour ne lancer cette vérification qu’après une traversée de la rivière,
• s’il y a au moins une licorne sur la rive gauche, alors il y a au moins autant de licornes que de dragons sur la rive gauche,
• s’il y a au moins une licorne sur la rive droite, alors il y a au moins autant de licornes que de dragons sur la rive droite.

L’exécution de ce script par Cubicle produit, en quelques secondes, la solution suivante :

et, avec l’option dot 2, le dessin de cette solution dans l’arbre exploré par Cubicle :

Un clic sur l’arbre ci-dessus permet d’accéder à la version pdf sur laquelle on a intérêt à zoomer pour voir que la solution est un chemin dans cet arbre.

La « trace d’erreur » sans les vérifications intermédiaires donne une solution très lisible, grâce à un nommage judicieux des transitions :

Et la liste des états (dragons RG, licornes RG, dragons RD, licornes RD, direction du bateau) parcourus est

On remarque que la solution trouvée par Cubicle n’est pas la même que celle trouvée par parcours en largeur du graphe : ce problème a plusieurs solutions.

Soit d1 la distance entre le point de départ et le premier dépot. On a vu que d1=15 est trop important (il ne reste plus rien), et que d1=10 est trop important aussi (abandon d’une partie de la cargaison dans le désert). La valeur optimale de d1 est celle qui permet de placer exactement 60 sacs de couscous au dépot, ce qui permet de démarrer une récurrence sans perte de couscous. Comme il y a 3×30 sacs au début, il faut 2 allers-retours et un aller ce qui fait consommer 5×d1 sacs de couscous par le chameau, puisque la distance parcourue par celui-ci est 2×d1+2×d1+d1=5×d1. Comme il faut que cette quantité consommée soit 90-60=30 sacs, cela donne la valeur optimale de d1 : 5×d1=30 soit d1=6 lieues.

 ______📦📦🐪________________________

Il reste alors 30-6=24 lieues à parcourir, avec 60 sacs de couscous à livrer. En partant avec 30 sacs jusqu’au bout, on arrive avec 6 sacs de couscous ce qui n’est pas optimal (on a laissé 30 sacs en plein désert). Soit alors d2 la distance au bout de laquelle on va constituer un second dépot. Pour optimiser il faut que l’aller-retour suivi d’un aller simple fasse consommer par le chameau, une des deux cargaisons de 30 sacs. Alors 2×d2+d2=3×d2=30 d’où d2=10. On porte donc 30 sacs au point d1+d2=16

 ______📦_________📦🐪______________

Il en reste alors 20 (10 ont été consommés par le chameau), on en laisse 10 sur place et on repart avec les 10 restants pour permettre au chameau de revenir vide au premier dépot :

 ______📦🐪_________📦______________

Puis il repart avec les 30 sacs restants jusqu’au second dépot, où il arrive avec 20 sacs :

 ________________📦🐪______________

Il finit les 14 lieues restantes avec ces 30 sacs. Il arrive alors avec 30-14=16 sacs. C’est le maximum qu’il puisse livrer. Cela représente environ 18 pourcent de la cargaison initiale.